Статистическая проверка гипотез. Лекция № 12

1. Математика, часть 2

Кафедра маркшейдерского дела
Математика, часть 2
Статистическая проверка гипотез
Лекция № 12

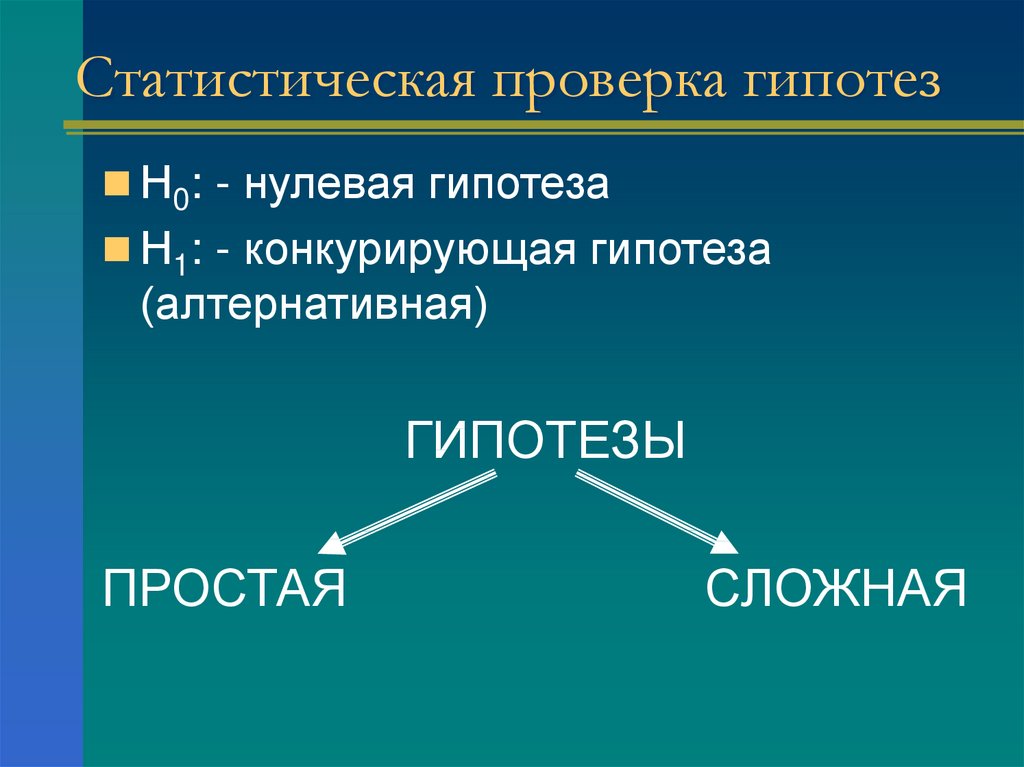
2. Статистическая проверка гипотез

Н0: - нулевая гипотеза
Н1: - конкурирующая гипотеза
(алтернативная)
ГИПОТЕЗЫ
ПРОСТАЯ
СЛОЖНАЯ

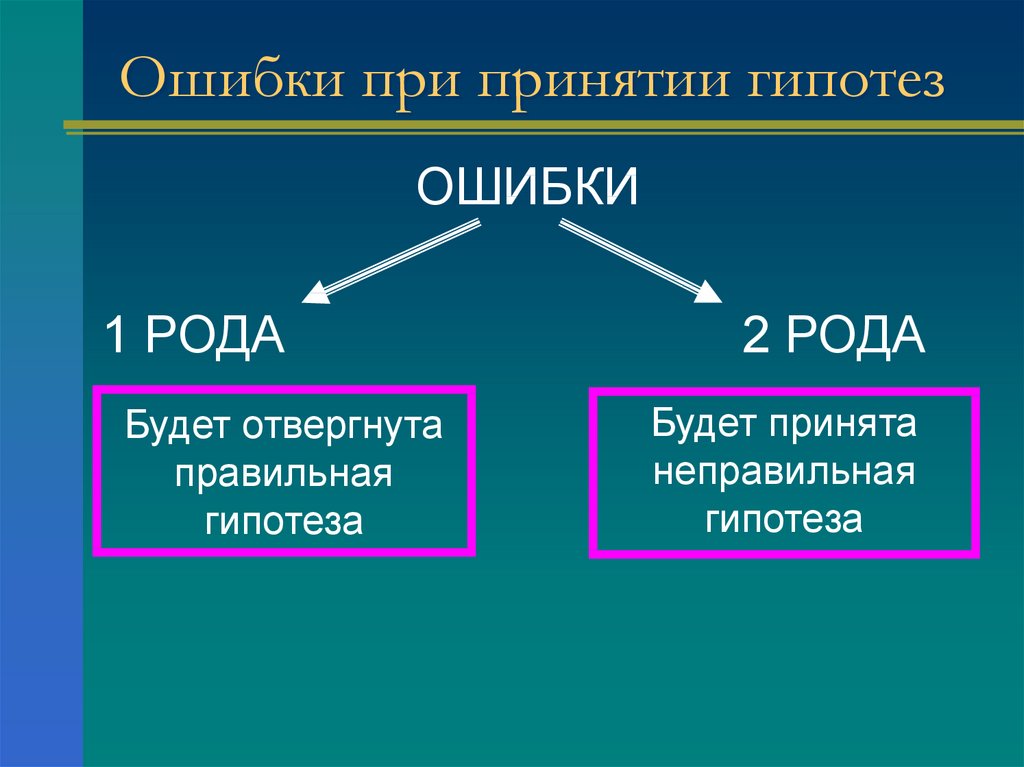
3. Ошибки при принятии гипотез

ОШИБКИ
1 РОДА
Будет отвергнута
правильная
гипотеза
2 РОДА
Будет принята
неправильная
гипотеза

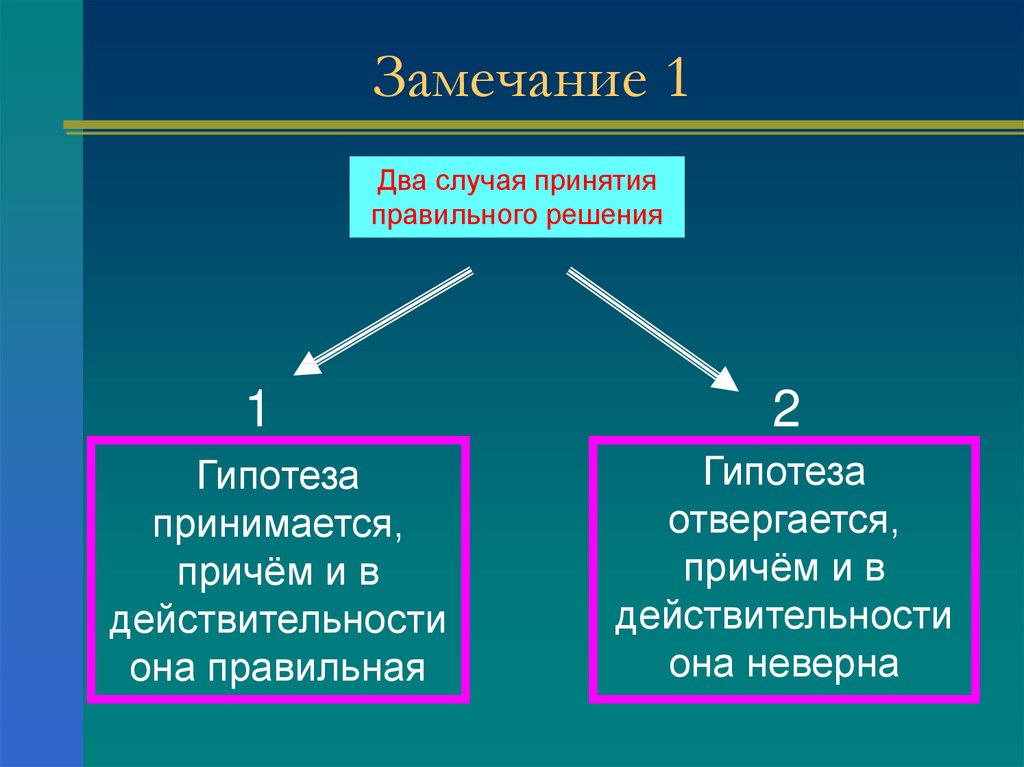
4. Замечание 1

Два случая принятия
правильного решения
1
Гипотеза
принимается,
причём и в
действительности
она правильная
2
Гипотеза
отвергается,
причём и в
действительности
она неверна

5. Замечание 2

Вероятность совершить ошибку первого рода
называют «УРОВЕНЬ ЗНАЧИМОСТИ» и
обозначают
0.05
Это означает, что в 5 случаях из 100
существует риск совершить ошибку 1 рода

6. Основные определения и понятия

Критическая область – совокупность
значения критерия, при которых
отвергают нулевую гипотезу Н0:
Область принятия гипотез –
совокупность значений критерия, при
которых гипотезу принимают
Критические точки – точки,
отделяющие критическую область от
области принятия решений

7. Основные определения и понятия

Принцип проверки гипотез – если критерий
принадлежит критической области,
нулевая гипотеза отвергается; если
принадлежит области принятия решений –
принимается
Существуют:
Односторонняя критическая область
1) Левосторонняя
2) правосторонняя
2. двусторонняя
1.

8. Критерий о равенстве средних

Проверяется нулевая гипотеза H0:
x1 x2
Альтернативная гипотеза
x1 x2
T
x1 x2
n2 n1
2
1
2
2
H1:
n1n2 n1 n2 2
n1 n2
СВ Т имеет закон распределения Стьюдента
с k=n1+n2-2 степенями свободы

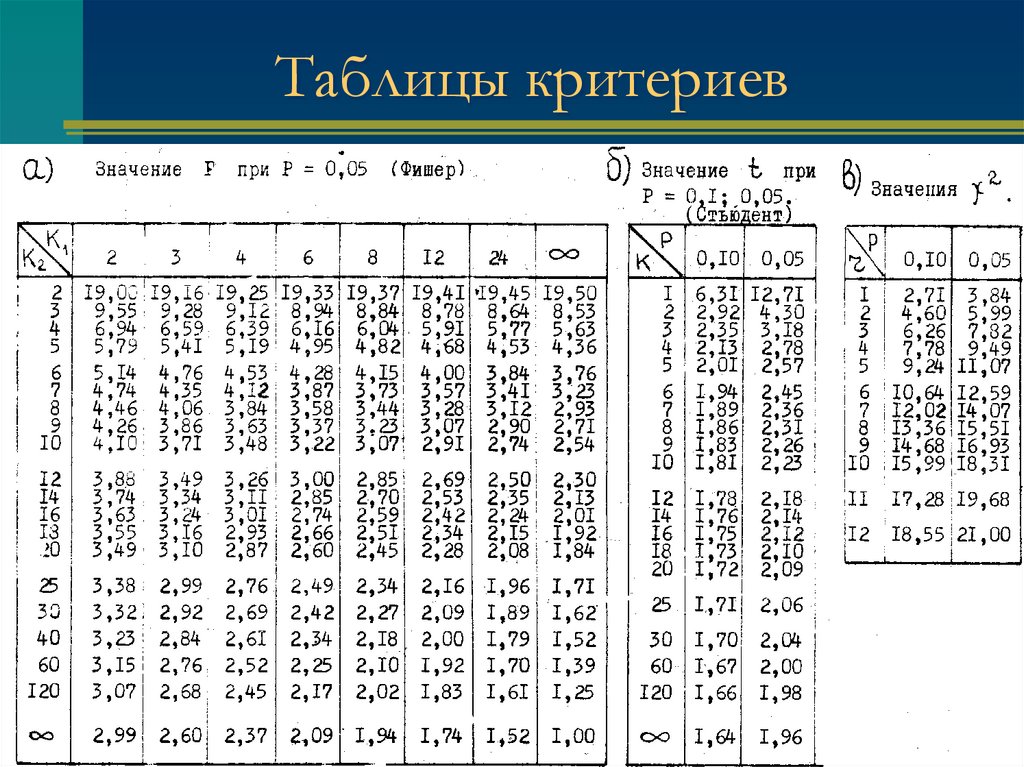
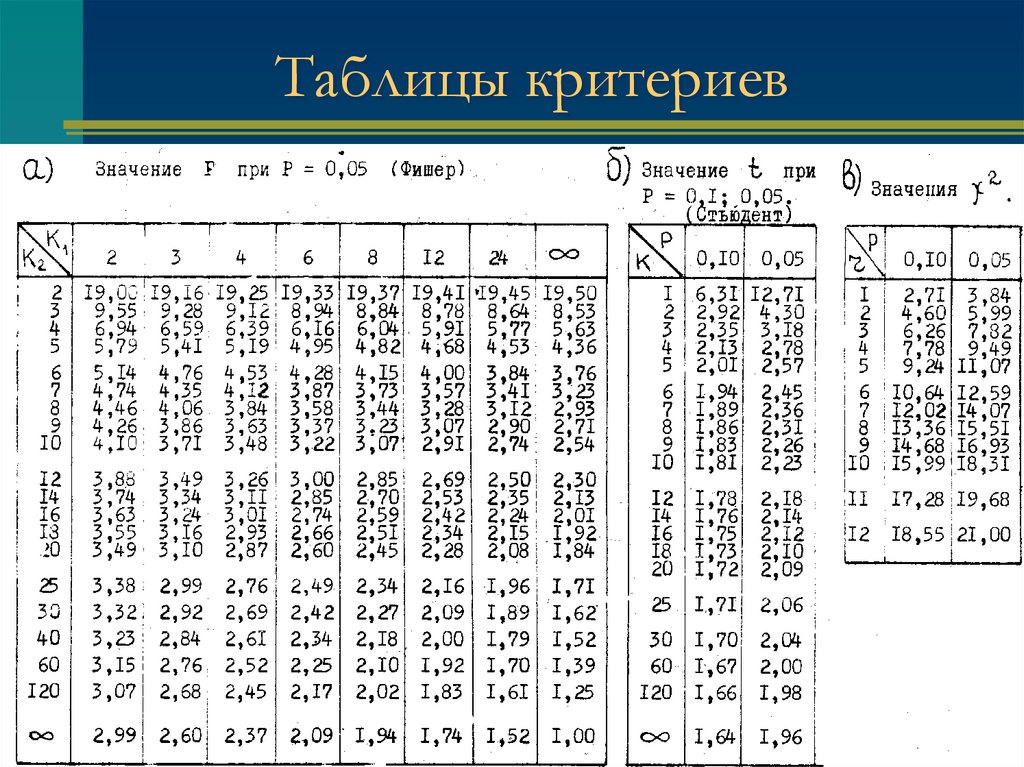
9. Таблицы критериев

10. Критерий однородности средних

Проверяется нулевая гипотеза H0:
x xi
Альтернативная гипотеза
x xi
T
x xi
ni n 2
;
2
n ni ni yi
H1:
yi
x xi
СВ Т имеет закон распределения Стьюдента
с k=n-2 степенями свободы

11. Таблицы критериев

12. Критерий о равенстве дисперсий

Проверяется нулевая гипотеза H0:
1 2
Альтернативная гипотеза
1 2
F
;
2
1
2
2
H1:
1 2
СВ Т имеет закон распределения Фишера
с k1 = n1 - 1 и k2 = n2 - 1 степенями свободы

13. Таблицы критериев

14. Критерий (Уилкоксона) о принадлежности двух выборок к одной генеральной совокупности

Пусть имеется две выборки из генеральной совокупности
X x1 , x2 , x3 , x4 , x5 ; Y y1 , y2 , y3 , y4
Расположим данные в порядке возрастания, к примеру так
x1 , x2 , y1 , y2 , y3 , x3 , y4 , x4 , x5
Если некоторому значению Х предшествует некоторый
У, то такая пара образует инверсию. Так Х3 даёт 3
инверсии, Х4 и Х5 по четыре инверсии, всего
U 3 4 4 11

15. Критерий (Уилкоксона) о принадлежности двух выборок к одной генеральной совокупности

При n>10 и m>10 распределение числа инверсий близко к
нормальному закону распределения с математическим
ожиданием
n*m
MU
2
И стандартом
n*m
n m 1
U
12
Тогда доверительный интервал запишется:
JU M U t U M U t U

16. Пример

Жила опробована двумя способами. Оценить, принадлежат ли
результаты к одной генеральной совокупности, т.е. равноценны
ли 2 метода
№№
Способ 1
Способ 2
№№
Способ 1
Способ 2
1
2
3
4
5
6
1.27
12.30
0.32
3.96
1.70
1.32
2.48
5.51
4.09
4.57
2.73
1.33
7
8
9
10
11
12
9.28
1.22
3.94
0.65
4.85
7.56
7.95
2.22
7.67
0.36
6.00
9.37

17. Пример

Расположим данные в порядке возрастания
x
y1 x
x
0.32
0.36
x
y6 y7 x
3.98
4.09
x
0.65 1.22 1.27
x
y2 x
y3 y4 y5 x
1.32
1.33 1.70
2.22 2.48 2.73
y8 y9 x
4.57 4.85 5.51
6.00
y10 y11 x
7.56 7.67
3.94
y12 x
7.95 9.28 9.37
Число инверсий:
U 1 1 1 1 2 5 5 7 9 11 12 55
12.3

18. Пример

12 *12
MU
72
2
12 *12
12 12 1 17.3
U
12
t 1.96 *17.3 34
JU 72 34 72 34 38 106
ВЫВОД: Выборки принадлежат к одной генеральной
совокупности,
Расхождений в опробовании двумя способами нет