Дискретное преобразование Фурье. Практическое применение ДПФ

1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»

Дискретное преобразование
Фурье. Практическое
применение ДПФ
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)

2. ЭФФЕКТ РАСТЕКАНИЯ СПЕКТРА (1)

Растекание
спектра
–
появление
дополнительных
2
(побочных)
составляющих в спектральном составе последовательности (сигнала)
при вычислении ДПФ.
Растекание спектра появляется в том случае, если на длительности
сигнала укладывается нецелое число периодов.
Побочные спектральные составляющие не имеют физического
смысла.
Эффект растекания спектра наблюдается в том случае, если хотя бы
для одной дискретной гармоники с частотой fi на длительности NT
укладывается нецелое число периодов Ti.
Отношение Pi = NT / Ti представляет собой нецелое число.

3. ЭФФЕКТ РАСТЕКАНИЯ СПЕКТРА (2)

3
Частота гармоники fi = Pi Δf представляет собой число, некратное
периоду дискретизации по частоте.
В периодическом продолжении гармоники появятся разрывы на
границах периода последовательности (это приводит к расширению
спектра).
Эффект растекания спектра принципиально неустраним (если на
длительности сигнала укладывается нецелое число периодов), но
может быть значительно уменьшен путем применения весовых
функций (окон).
Окна
–
вещественные
неотрицательные
последовательности,
максимальные в центре и монотонно спадающие к границам, что
ослабляет влияние разрывов при периодическом продолжении.

4. УЛУЧШЕНИЕ РАЗЛИЧЕНИЯ ГАРМОНИК С БЛИЗКО РАСПОЛОЖЕННЫМИ ЧАСТОТАМИ (1)

4
УЛУЧШЕНИЕ РАЗЛИЧЕНИЯ ГАРМОНИК
С БЛИЗКО РАСПОЛОЖЕННЫМИ ЧАСТОТАМИ (1)
Разрешение по частоте
f fд N
Улучшение различения гармоник
с близко расположенными частотами
f f1 f 2 2 f
Дополнение исходной последовательности нулями
L
1)
Восстановление
fд
f1 f 2 f
спектральной
дискретизации по частоте
f f д L
плотности
с
периодом

5. УЛУЧШЕНИЕ РАЗЛИЧЕНИЯ ГАРМОНИК С БЛИЗКО РАСПОЛОЖЕННЫМИ ЧАСТОТАМИ (2)

5
УЛУЧШЕНИЕ РАЗЛИЧЕНИЯ ГАРМОНИК
С БЛИЗКО РАСПОЛОЖЕННЫМИ ЧАСТОТАМИ (2)
2)
По
графику
модуля
спектральной
плотности
определение
ближайших пиков с максимальными амплитудами на частотах,
близких к f1 и f2.
3) В общем случае частоты f1 и f2 могут быть некратны новому
периоду дискретизации и в этом случае они будут определяться с
погрешностью.
Применение MATLAB для улучшения различения гармоник
с близко расположенными частотами
Функция fft: X = fft(x,L).
L – длина последовательности после автоматического дополнения
нулями.

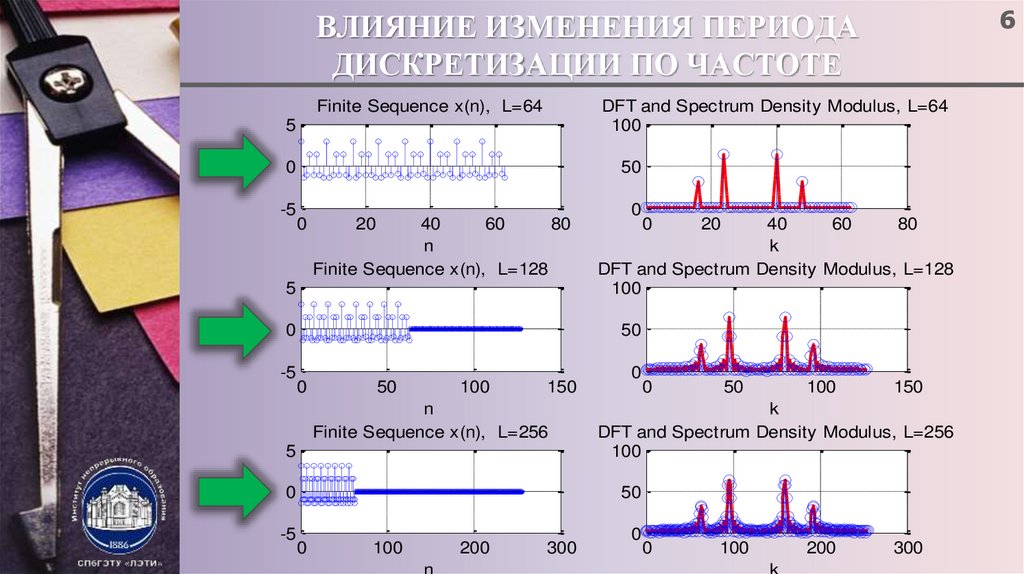
6. ВЛИЯНИЕ ИЗМЕНЕНИЯ ПЕРИОДА ДИСКРЕТИЗАЦИИ ПО ЧАСТОТЕ

6
ВЛИЯНИЕ ИЗМЕНЕНИЯ ПЕРИОДА
ДИСКРЕТИЗАЦИИ ПО ЧАСТОТЕ
Finite Sequence x(n), L=64
DFT and Spectrum Density Modulus, L=64
100
5
0
-5
50
0
20
40
60
80
n
Finite Sequence x(n), L=128
5
0
-5
0
20
40
60
80
k
DFT and Spectrum Density Modulus, L=128
100
50
0
50
100
150
n
Finite Sequence x(n), L=256
5
0
-5
0
0
0
50
100
150
k
DFT and Spectrum Density Modulus, L=256
100
0
100
50
0
100
200
n
300
0
200
k
300

7. ПРИМЕР. ЭФФЕКТ РАСТЕКАНИЯ СПЕКТРА

Amplitude Spectrum of the Periodic Sequence N=64
N
1/N|X (k)|
1
0.5
0
0
10
20
30
40
50
60
k
Amplitude Spectrum of the Periodic Sequence M=71
0
10
20
30
70
M
1/M|X (k)|
1
0.5
0
40
k
50
60
70
7

8. ПРИМЕР. УМЕНЬШЕНИЕ ЭФФЕКТА РАСТЕКАНИЯ СПЕКТРА

8
ПРИМЕР. УМЕНЬШЕНИЕ ЭФФЕКТА
РАСТЕКАНИЯ СПЕКТРА
Amplitude spectrum without windowing M=71
M
|1/M X (k)|
1
0.5
0
0
10
0
10
20
30
40
50
60
k
Amplitude spectrum with Hamming Window M=71
20
30
70
0.6
M
|1/M XW (k)|
0.8
0.4
0.2
0
40
k
50
60
70

9. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»

Дискретное преобразование
Фурье. Практическое
применение ДПФ
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)