Похожие презентации:
Адаптивные фильтры. Практическое применение (2)
1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Адаптивные фильтры.Практическое
применение (2)
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)
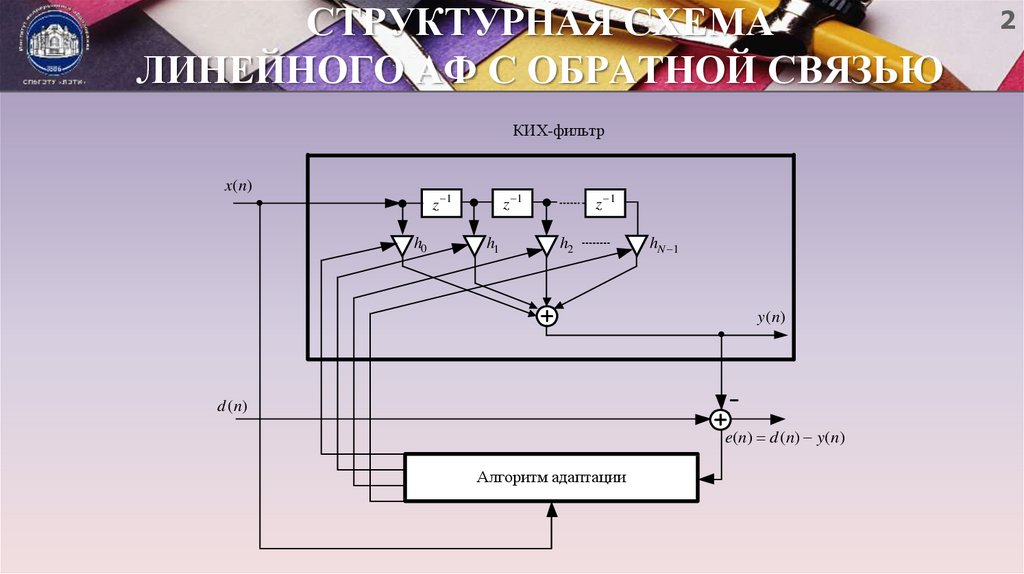
2. СТРУКТУРНАЯ СХЕМА ЛИНЕЙНОГО АФ С ОБРАТНОЙ СВЯЗЬЮ
КИХ-фильтрx ( n)
z 1
z 1
h0
h1
z 1
h2
hN 1
y ( n)
d ( n)
e( n ) d ( n ) y ( n )
Алгоритм адаптации
2
3. ЦЕЛИ ИССЛЕДОВАНИЯ
1) изучить метод эхоподавления (эхокомпенсации) наоснове адаптивной фильтрации с использованием
структуры прямой идентификации;
2) выполнить компьютерное моделирование метода
эхоподавления в среде MATLAB;
3) исследовать качество эхоподавления на основе
выбранных критериев;
4) выполнить компьютерное моделирование
эхоподавления в среде MATLAB при различных
моделях сигналов.
3
4. ПРЯМАЯ ИДЕНТИФИКАЦИЯ НА ОСНОВЕ АФ
Схема прямой идентификацииНеизвестная
система
x(n)
Адаптивный
фильтр
d (n)
y(n)
e(n)
4
5. ПРЯМАЯ ИДЕНТИФИКАЦИЯ НА ОСНОВЕ АФ. ТИПОВЫЕ СИГНАЛЫ
1) x(n) – входной сигнал АФ (входной сигналнеизвестной системы);
2) d(n) – образцовый сигнал АФ (выходной сигнал
неизвестной системы);
3) y(n) – выходной сигнал АФ;
4) e(n) – сигнал ошибки АФ (разность между
образцовым сигналом и выходным сигналом АФ).
5
6. СХЕМА ПРЯМОЙ ИДЕНТИФИКАЦИИ ПРИ ЭХОПОДАВЛЕНИИ
Схема прямой идентификацииНеизвестная система
Неизвестная система
x2 (nx)2 (n)xСР (n)xСР (n)
Формирователь эхоФормирователь
эхосигнала
сигнала
x(n) x1(n)
x(n) x1(n)
Адаптивный
фильтр
Адаптивный
фильтр
x1Эx(1Э
n) (n)
d (n) xd
НС
(n(n)) xНС
(n)d(n D)
z D
z D
y(n) xˆ1Э (n)
d (n D)
e(n) xˆ2 (n)
y(n) xˆ1Э (n)
e(n) xˆ2 (n)
6
7. СХЕМА ПРЯМОЙ ИДЕНТИФИКАЦИИ ПРИ ЭХОПОДАВЛЕНИИ. ТИПОВЫЕ СИГНАЛЫ
71) x1(n), x2(n) – сигналы 1-го и 2-го источников;
2) x1Э(n) – эхо-сигнал 1-го источника; xСР(n) – шум
среды распространения;
3) y(n) – выходной сигнал АФ (оценка эхо-сигнала 1го источника);
4) e(n) – сигнал ошибки АФ (оценка сигнала 2-го
источника).
8. АЛГОРИТМ ЭХОПОДАВЛЕНИЯ НА ОСНОВЕ АФ (1)
8АЛГОРИТМ ЭХОПОДАВЛЕНИЯ НА ОСНОВЕ АФ (1)
1) Моделирование входного сигнала неизвестной системы (сигнала 1-го источника) x(n) =x1(n);
2) Моделирование формирователя эхо-сигнала (например, в виде КИХ-фильтра ФНЧ или КИХфильтра ПФ);
3) Моделирование сигнала 2-го источника x2(n);
4) Моделирование шума среды распространения xСР(n) (например, в виде нормального белого
шума с заданным СКО);
5) Вычисление реакции неизвестной системы (образцового сигнала АФ)
в виде суммы: d(n) = x1Э(n) + x2(n) + xСР(n) ;
6) Моделирование задержанного образцового сигнала d(n-D);
7) Моделирование структуры АФ с КИХ-фильтром (на основе объекта АФ);
8) Моделирование адаптивной фильтрации: вычисление y(n) ≈ x1Э(n) и
e(n) ≈ x2(n);
9) Сравнение сигналов x2(n) и e(n) ≈ x2(n) по среднеквадратическому критерию (RMSE – Root
Mean Squared Error);
10) Вычисление величины (степени) подавления эхо-сигнала Q.
9. АЛГОРИТМ ЭХОПОДАВЛЕНИЯ НА ОСНОВЕ АФ (2)
9АЛГОРИТМ ЭХОПОДАВЛЕНИЯ НА ОСНОВЕ АФ (2)
Вывод графиков в MATLAB:
1) Сигналы 1-го и 2-го источников x1(n) и x2(n) и их ДПФ;
2) Образцовый сигнал d(n) и его ДПФ;
3) Выходной сигнал АФ y(n) ≈ x1Э(n) и его ДПФ;
4) Сигнал ошибки АФ e(n) ≈ x2(n) и его ДПФ.
1) RMSE:
RMSE
1 L 1
2
x2 ( n ) xˆ2 (n )
L n 0
1 L 1
2
x2 ( n ) e( n )
L n 0
L 1
2) Подавление эхо-сигнала Q:
Q 10 lg
L 1
n 0
n 0
x1 ( n)
2
x2 ( n) e( n)
2
10. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ
102 f11
2 f12
2 f13
x1 ( n ) A11 cos
n A12 cos
n A13 cos
n
f
f
f
д
д
д
2 f 21
2 f 22
2 f 23
x2 ( n) A21 cos
n A22 cos
n A23 cos
n
f
f
f
д
д
д
f д 4000Гц L 3000 f11 200 Гц; f12 500 Гц; f13 1200 Гц
A11 1.5; A12 2.5; A13 4 f 21 300 Гц; f 22 700 Гц; f 23 1400 Гц
A21 0.5; A22 1; A23 0.1 N 40 порядок КИХ-фильтра в составе АФ
N1 int( N / 10) порядок КИХ-фильтра ФНЧ
(формирователь эхо сигнала);норм.частота разрыва 0.2
11. СИГНАЛ ОТ ИСТОЧНИКА 1 И ЕГО ДПФ
Signal from Source 1 (Input Signal of AF)10
0
-10
0
500
1000
1500
2000
n
DFT (Source 1)
2500
3000
4
2
0
0
1000
2000
f
3000
4000
11
12. ЭХО-СИГНАЛ И ЕГО ДПФ
Output signal of echo-system5
0
-5
0
500
1000
1500
2000
n
DFT (Echo signal)
2500
3000
3
2
1
0
0
1000
2000
f
3000
4000
12
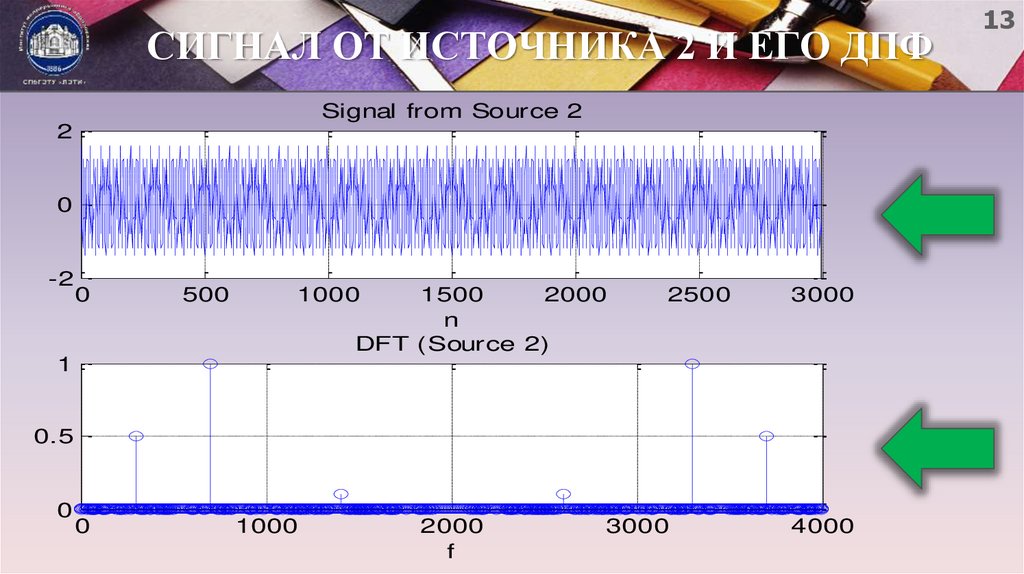
13. СИГНАЛ ОТ ИСТОЧНИКА 2 И ЕГО ДПФ
Signal from Source 22
0
-2
0
500
1000
1500
2000
n
DFT (Source 2)
2500
3000
1
0.5
0
0
1000
2000
f
3000
4000
13
14. ДПФ СИГНАЛОВ ОТ ИСТОЧНИКА 1 И ИСТОЧНИКА 2
DFT of Signals from Source 1 and Source 24
3.5
3
AS - Source 1
AS - Source 2
2.5
2
1.5
1
0.5
0
0
1000
2000
f
3000
4000
14
15. ОЦЕНКА СИГНАЛА ОТ ИСТОЧНИКА 2 (ПОСЛЕ ЭХОПОДАВЛЕНИЯ) И ЕГО ДПФ
Signal from Source 2 after Echo Suppression4
2
0
-2
0
3000
2500
2000
1500
n
DFT (Signal from Source 2 after Echo Suppression)
500
1000
1
0.5
0
0
1000
2000
f
3000
4000
15
16. ДПФ СИГНАЛОВ ОТ ИСТОЧНИКА 2 (ИСХОДНЫЙ И ПОСЛЕ ЭХОПОДАВЛЕНИЯ)
16ДПФ СИГНАЛОВ ОТ ИСТОЧНИКА 2
(ИСХОДНЫЙ И ПОСЛЕ ЭХОПОДАВЛЕНИЯ)
DFT of Signal from Source 2 after Echo Suppression and Original Signal from Source 2
1
0.9
0.8
Signal from Source 2 after Echo Suppression
AS - Source 2
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
500
1000
1500
2000
f
2500
3000
3500
4000
17. МОДЕЛИРОВАНИЕ ЭХОПОДАВЛЕНИЯ ПРИ ИСПОЛЬЗОВАНИИ СИГНАЛОВ С ОГРАНИЧЕННЫМ СПЕКТРОМ (1)
Fs = 4000 Гц; f0 = 300 Гц; L = 4000Signal from Source 1 (Input Signal of AF)
1
Signal from Source 1 (Fragment)
1
0.5
0.5
0
0
-0.5
-0.5
-1
0
0.5
1
t
DFT
1.5
2
-1
0.98
0.03
0.03
0.02
0.02
0.01
0.01
0
0
1000
2000
f
3000
4000
0
0
1
1.02
1.04
t
DFT (Fragment)
500
1000
f
1500
1.06
2000
17
18. МОДЕЛИРОВАНИЕ ЭХОПОДАВЛЕНИЯ ПРИ ИСПОЛЬЗОВАНИИ СИГНАЛОВ С ОГРАНИЧЕННЫМ СПЕКТРОМ (2)
DFT (Echo signal)0.02
0.015
0.01
0.005
0
260
270
280
290
300
310
f
320
330
340
18
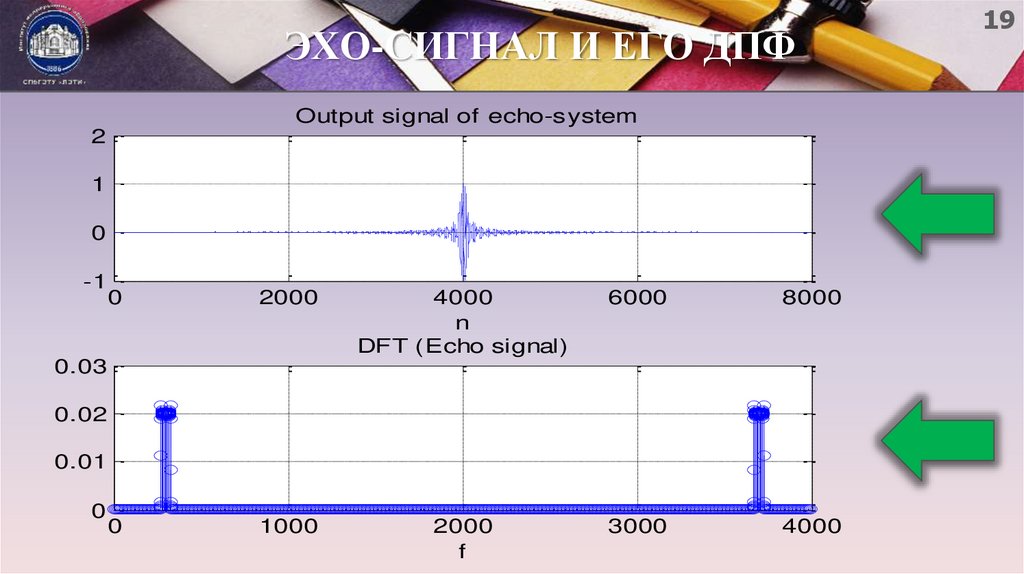
19. ЭХО-СИГНАЛ И ЕГО ДПФ
Output signal of echo-system2
1
0
-1
0
2000
4000
n
DFT (Echo signal)
6000
8000
0
1000
2000
f
3000
4000
0.03
0.02
0.01
0
19
20. СИГНАЛ ОТ ИСТОЧНИКА 2 И ЕГО ДПФ (1)
Signal from Source 2Signal from Source 2 (Fragment)
1
1
0
-1
0
0
1
t
DFT
2
-1
0.95
0.03
0.03
0.02
0.02
0.01
0.01
0
0
2000
4000
0
0
1
t
DFT (Fragment)
1.05
1000
2000
20
21. СИГНАЛ ОТ ИСТОЧНИКА 2 И ЕГО ДПФ (2)
DFT (Fragment)0.02
0.018
0.016
0.014
0.012
0.01
0.008
0.006
0.004
0.002
0
670
680
690
700
710
f
720
730
21
22. ДПФ СИГНАЛОВ ОТ ИСТОЧНИКА 1 И ИСТОЧНИКА 2
DFT of Signals from Source 1 and Source 20.025
0.02
0.015
AS - Source 1
AS - Source 2
0.01
0.005
0
0
1000
2000
f
3000
4000
22
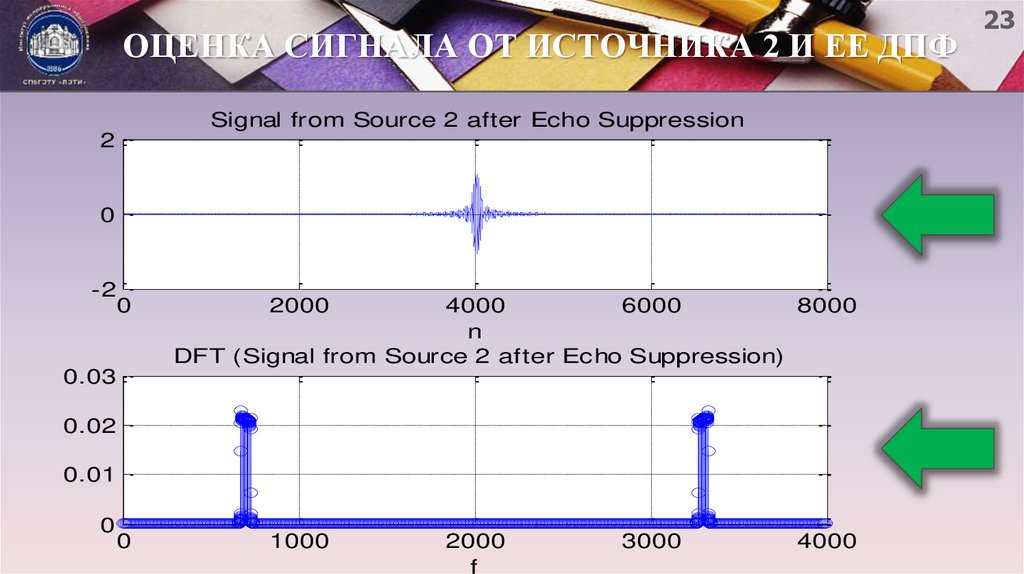
23. ОЦЕНКА СИГНАЛА ОТ ИСТОЧНИКА 2 И ЕЕ ДПФ
Signal from Source 2 after Echo Suppression2
0
-2
0
2000
4000
6000
8000
n
DFT (Signal from Source 2 after Echo Suppression)
0.03
0.02
0.01
0
0
1000
2000
f
3000
4000
23
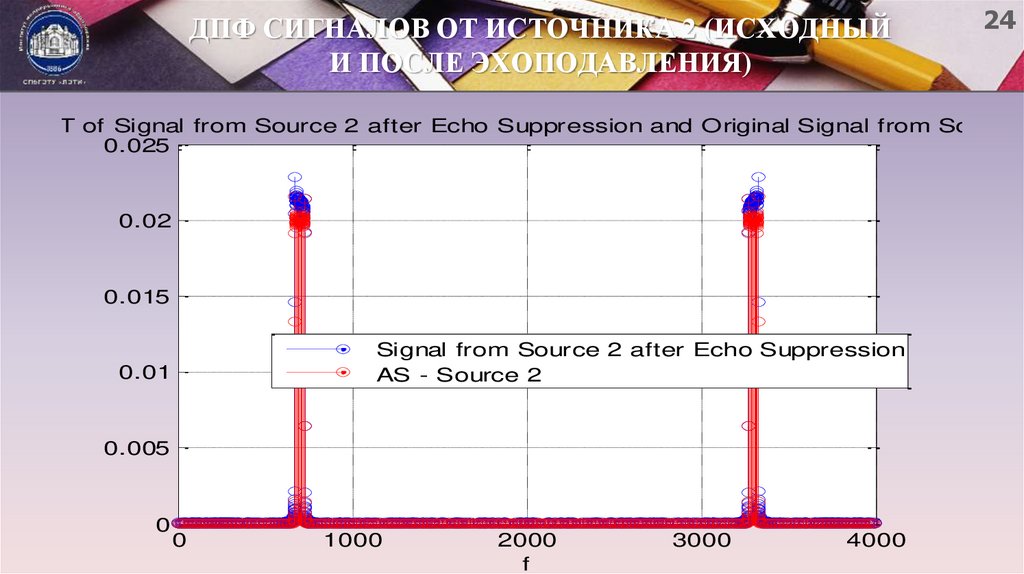
24. ДПФ СИГНАЛОВ ОТ ИСТОЧНИКА 2 (ИСХОДНЫЙ И ПОСЛЕ ЭХОПОДАВЛЕНИЯ)
24DFT of Signal from Source 2 after Echo Suppression and Original Signal from Source
0.025
0.02
0.015
Signal from Source 2 after Echo Suppression
AS - Source 2
0.01
0.005
0
0
1000
2000
f
3000
4000
25. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Адаптивные фильтры.Практическое
применение (2)
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)




















 Математика
Математика








