Фильтрация шумов

1. Фильтрация шумов

Лекции по курсу
«Электроника систем регистрации элементарных частиц»
Жуланов Владимир Викторович
тел. 329-47-32
e-mail: [email protected]

2.

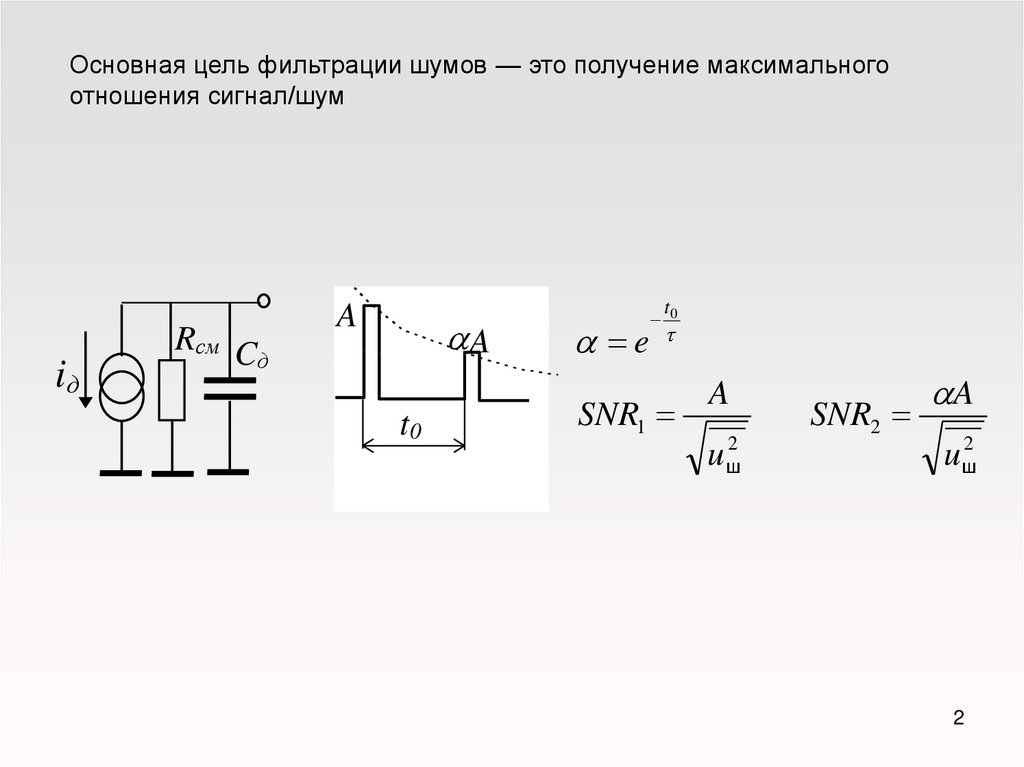
Основная цель фильтрации шумов — это получение максимального
отношения сигнал/шум
iд
Rсм C
д
A
aA
t0
a e
t0
SNR1
A
uш2
SNR2
aA
uш2
2

3.

A
aA
t0
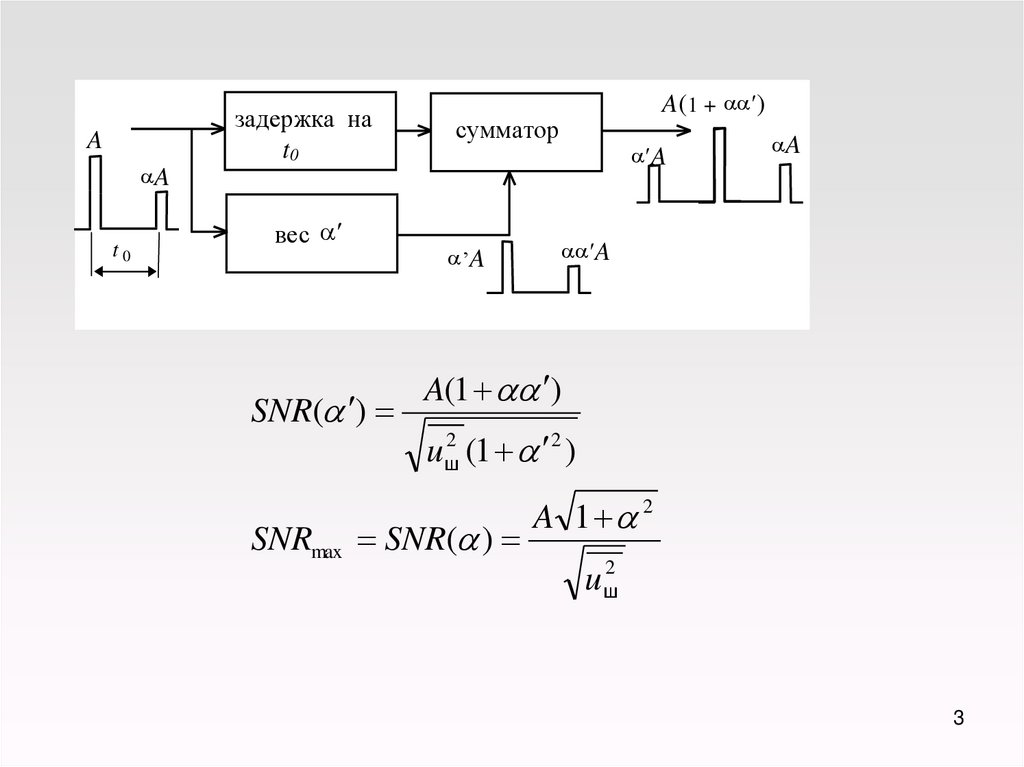
задержка на
t0
вес a
SNR(a )
A(1 + aa )
сумматор
a’A
a A
aA
aa A
A(1 aa )
uш2 (1 a 2 )
SNRmax SNR(a )
A 1 a 2
uш2
3

4.

A
Aa
Ab
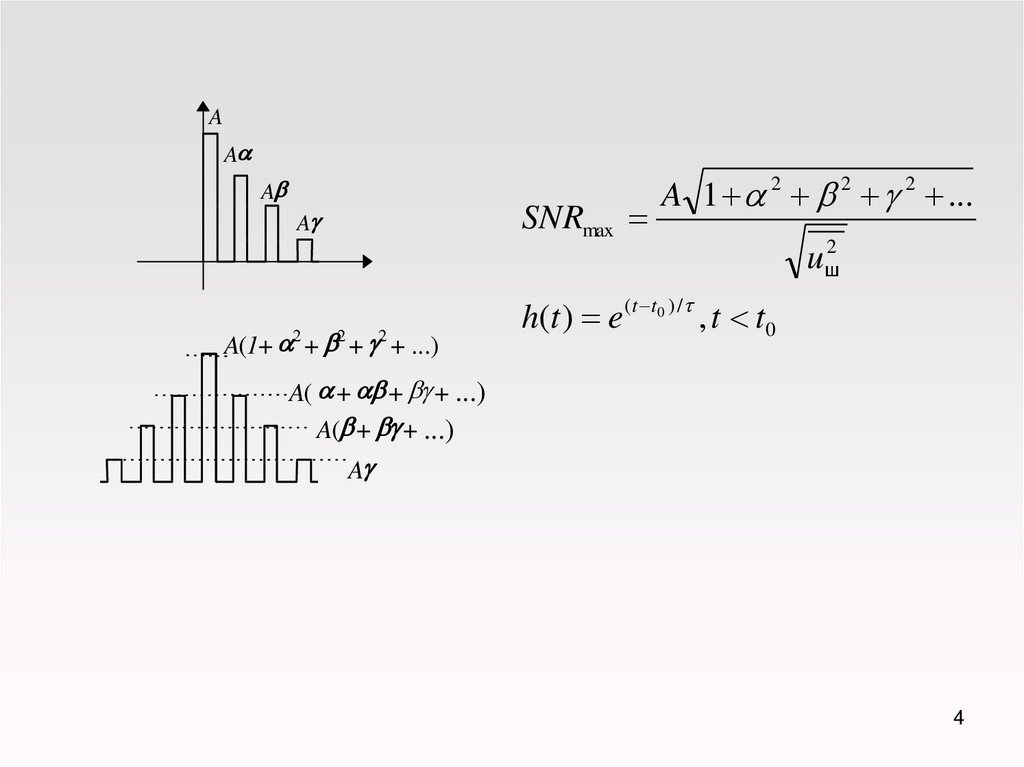
SNRmax
Ag
A(1+ a2 + b2 + g2 + ...)
A 1 a 2 b 2 g 2 ...
uш2
h(t ) e (t t0 ) / , t t0
A( a + ab + bg + ...)
A(b + bg + ...)
Ag
4

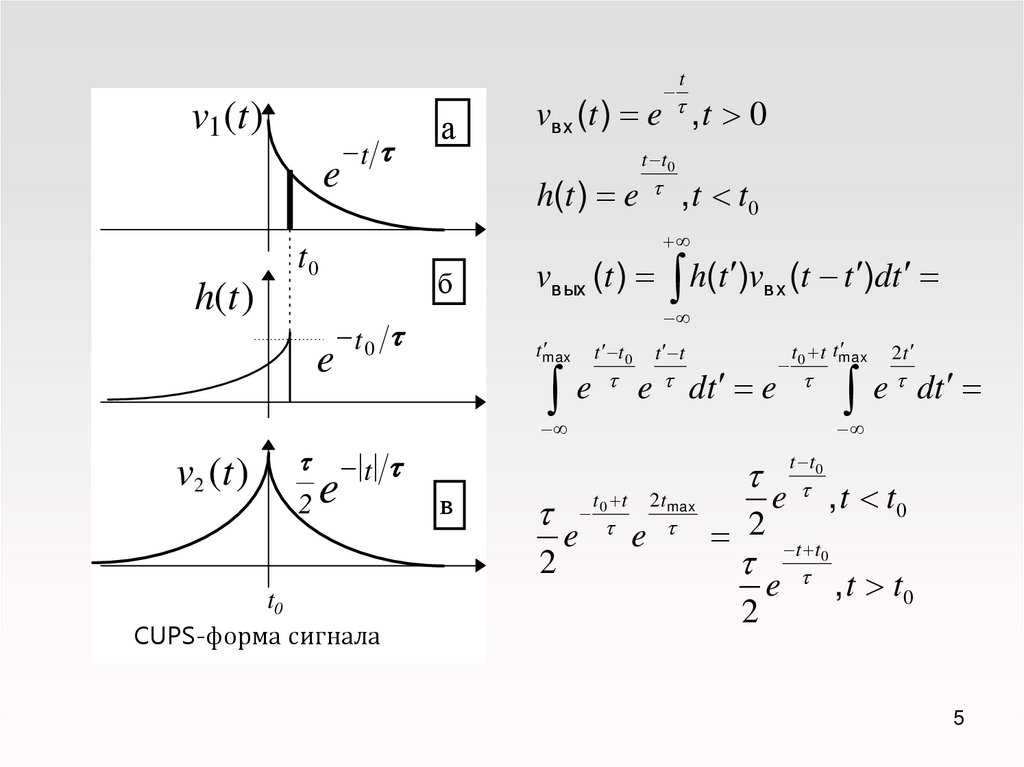
5.

v1 (t )
e
t
e
vв х (t ) e , t 0
h(t ) e
t t 0
, t t0
t0
h(t )
а
t
б
vв ых (t )
h(t )v
вх
(t t )dt
t0
tmax
t t 0
e
t t
e
dt e
t 0 t tmax
v 2 (t )
2e
2
t0
CUPS-форма сигнала
e
e dt
t
в
2t
t0 t
2 tmax
e
2
2
t t0
e
, t t0
t t0
e
, t t0
5

6. Сравнительный анализ фильтров методом шумовых индексов

Основные критерии при выборе параметров фильтров:
•Отношение сигнал/шум (SNR)
•Загрузочная способность
•Чувствительность к длительности сигналов с детектора
6

7.

Время-инвариантный фильтр
— это фильтр, параметры,
которого не зависят от
наличия сигнала.
+
Rb
Детектор
U s2
A(jw)
~
Cd
I
2
p
Выход
U in2
шум «Step»
сигнал
выход
Параллельный и
последовательные шумы
представляем, как случайные
последовательности маленьких
импульсов со средними
частотами ns и n
соответственно
ФИЛЬТР
шум «Delta»
7

8.

N dt ns dt DN dt ns dt
Tm
dt
t
t1
u вх ans dt u вых ans R(t1 )dt
Du вых a R (t1 ) DN dt a R (t1 ) ns dt
2
2
ns
2
Ns 2
Ac
2
2
R(t )
2
dt
0
Дельта импульс представляем, как две ступеньки амплитудой 1/ t,
противоположной полярности сдвинутые, на t
Через время t1 реакция системы на такую пару импульсов будет:
1
( R(t1 t ) R(t1 )) R (t1 )
t
Аналогично:
ns
N 2
Ac
2
R (t ) dt
2
0
8

9. Пример для RC-CR-фильтра

Передаточная функция:
t
R(t ) k e
t
(1 )
2
e t
, Ac R( ) k , R (t ) k 1
e
t
2
2 (1 )
t
e
N s2 ns e dt ns ns 1.847
4
0
t
2
e
1.847
2
N n
n
4
n
опт
ns
9

10. Пример для трапецеидального фильтра

f(t)
Пример для трапецеидального фильтра
a
1
2
3
t
R(t)
б
R (t)
t
в
R2(t)
г
3 2
1 2
2
1 3
t
t
2
N s ns 2 dt dt 2 dt ns ( 2
)
3
0
0 3
0 1
3
1
1
1
1 1
2
N n 2 dt 2 dt n ( )
1 3
1
3
0
0
[R (t)] 2
д
.
10

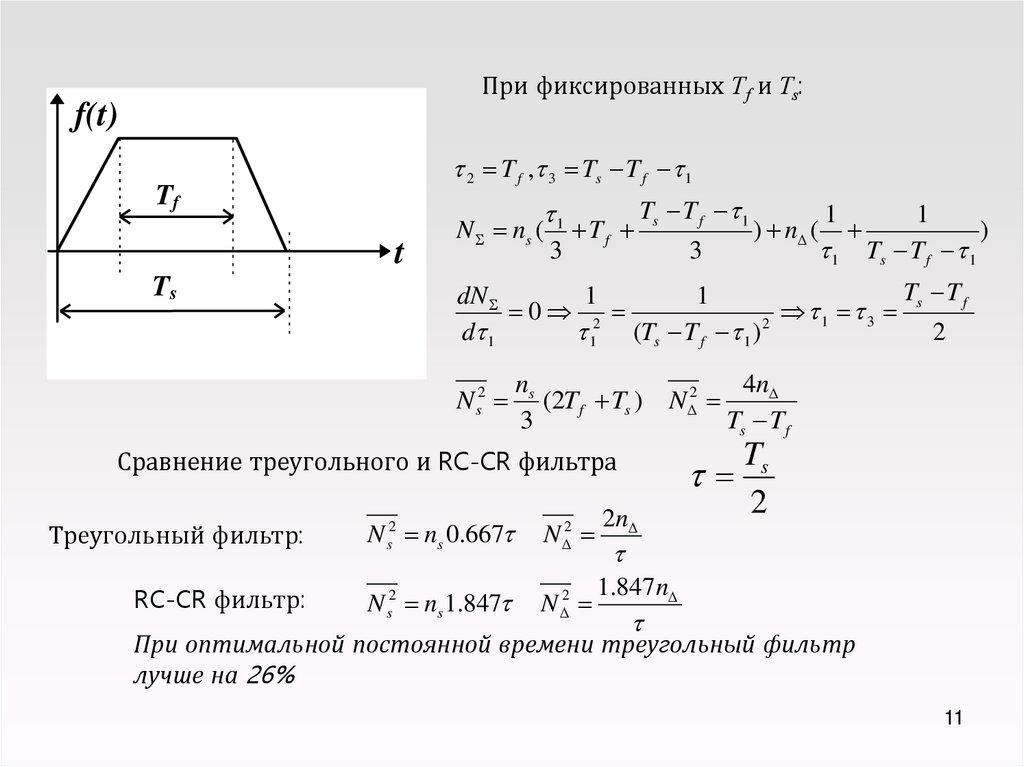
11.

При фиксированных Tf и Ts:
f(t)
2 T f , 3 Ts T f 1
Tf
t
Ts
N ns (
1
3
Tf
Ts T f 1
3
) n (
1
1
1
)
Ts T f 1
Ts T f
dN
1
1
0 2
1 3
d 1
1 (Ts T f 1 ) 2
2
N s2
ns
(2T f Ts )
3
N 2
Сравнение треугольного и RC-CR фильтра
Треугольный фильтр:
N s2 ns 0.667
N 2
2n
RC-CR фильтр:
N s2 ns 1.847
N 2
1.847n
4n
Ts T f
Ts
2
При оптимальной постоянной времени треугольный фильтр
лучше на 26%
11

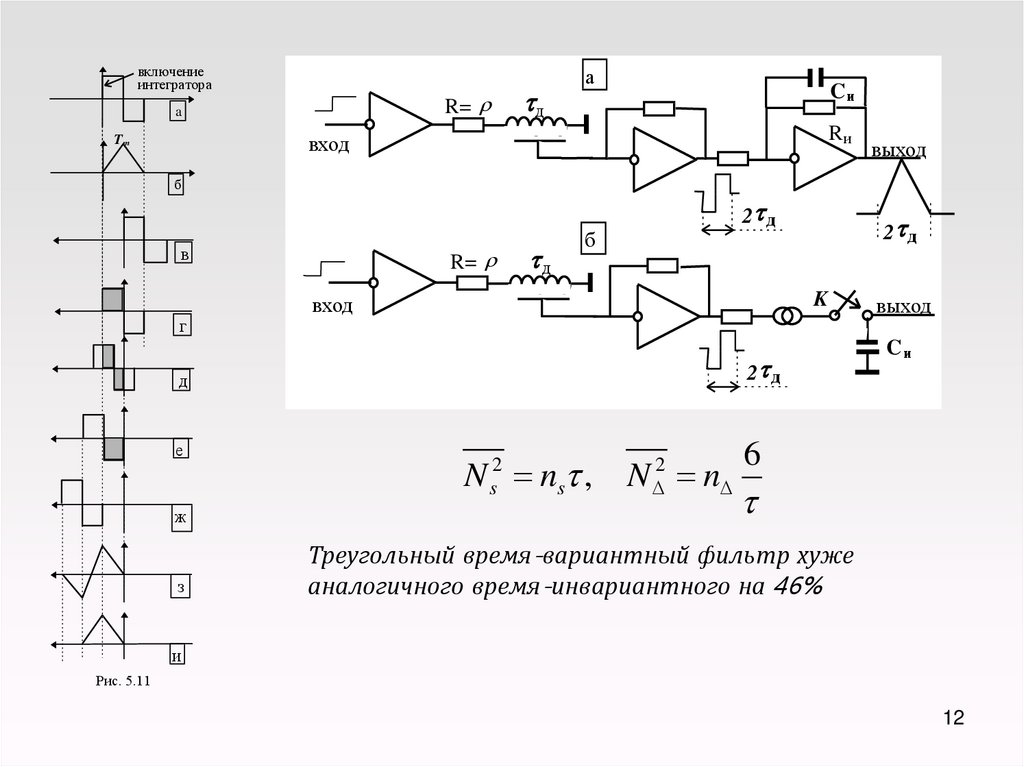
12.

включение
интегратора
R= r
a
д
а
Cи
Rи
вход
Tm
выход
б
R= r
в
д
2 д
б
2 д
K
вход
г
2 д
д
е
ж
з
N ns ,
2
s
N n
2
выход
Cи
6
Треугольный время-вариантный фильтр хуже
аналогичного время-инвариантного на 46%
и
Рис. 5.11
12

13. Фильтр «RC-CR+управляемый интегратор»

Применяя дополнительный
интегратор, можно несколько
улучшить шумовую характеристику
или увеличить быстродействие
системы:
t
td
Например, если
tg
t g /
относительный
шум
опт
0.2;
g
2.5
то относительный шум = 1, а
быстродействие увеличено в 5
раз
0
0,5
1,0
1,6
1,0 0,927 0,887 0,87
1,7
1,8
2,5 4,2
10,0
0,87 0,87 0,886 1,0
1,55
13

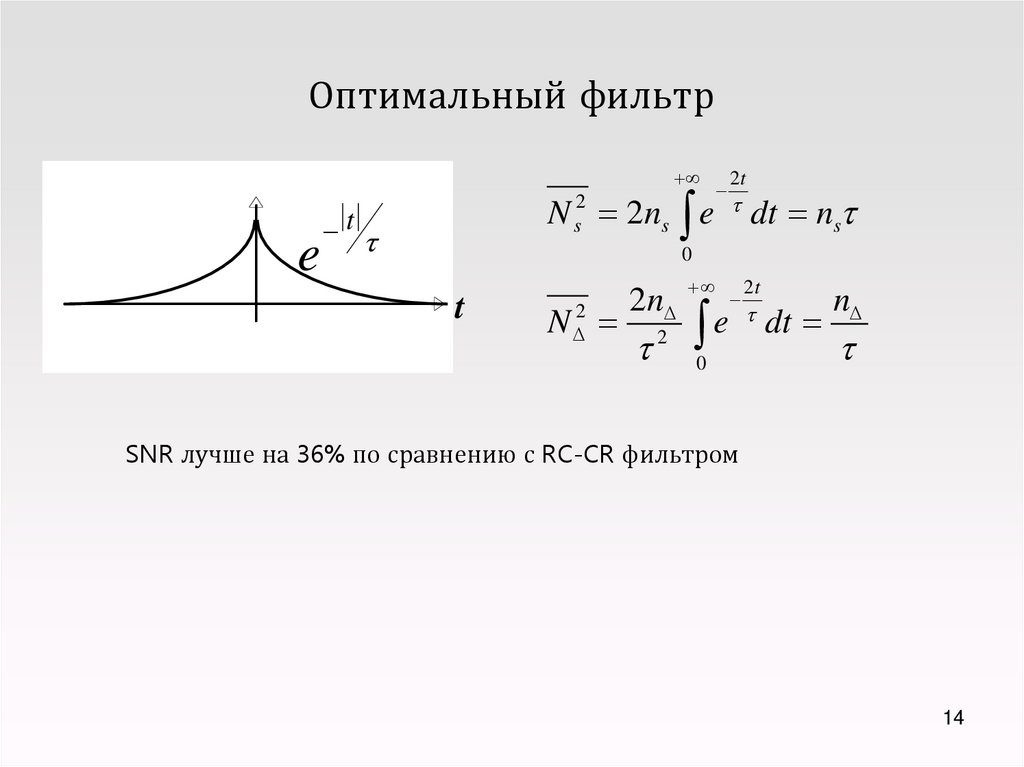
14. Оптимальный фильтр

e
t
2t
e
N s2 2ns e
dt ns
0
t
N
2
2n
2
0
2t
dt
n
SNR лучше на 36% по сравнению с RC-CR фильтром
14

15. Резюме

• Оптимальная фильтрация
• Сравнительный анализ фильтров методом шумовых индексов. RC-CR
фильтр. Время-инвариантный трапецеидальный фильтр. Время
вариантный фильтр. Фильтр «RC-CR+управляемый интегратор»
• Оптимальный фильтр
15