Оптимальный прием сигналов без памяти (лекция 3)

1. Оптимальный прием сигналов без памяти

Лекция № 3

2.

При модуляции без памяти каждому информационному символу m
ставится в соответствие сигнал конечной длительности sm(t).
Набор
информационных
бит
Набор
информационных
символов, m
00
0
s0(t)
01
1
s1(t)
10
2
s2(t)
11
3
s3(t)
Ансамбль
сигналов

3.

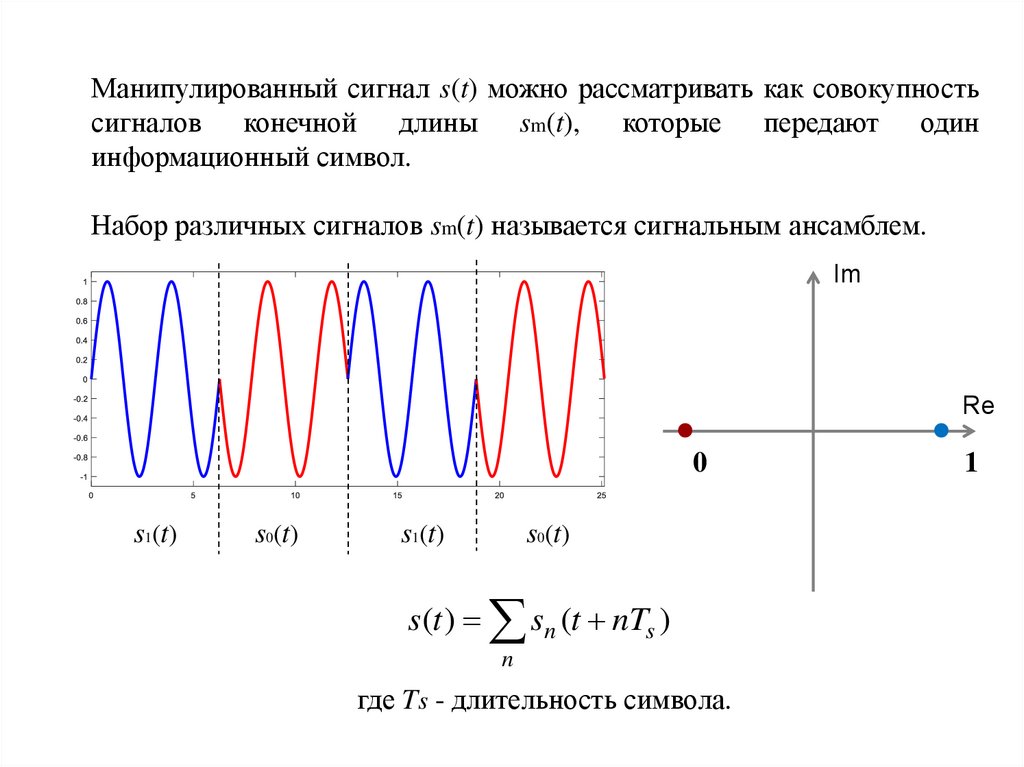
Манипулированный сигнал s(t) можно рассматривать как совокупность
сигналов конечной длины sm(t), которые передают один
информационный символ.
Набор различных сигналов sm(t) называется сигнальным ансамблем.
Im
Re
0
s1(t)
s0(t)
s1(t)
s(t )
s0(t)
sn (t nTs )
n
где Ts - длительность символа.
1

4.

Манипулированный сигнал s(t) можно рассматривать как совокупность
сигналов конечной длины sm(t), которые передают один
информационный символ.
Набор различных сигналов sm(t) называется сигнальным ансамблем.
Для ЧМн сигналов не
имеет смысла строить
«звездную» диаграмму.
s1(t)
s0(t)
s1(t)
s(t )
s0(t)
sn (t nTs )
n
где Ts - длительность символа.

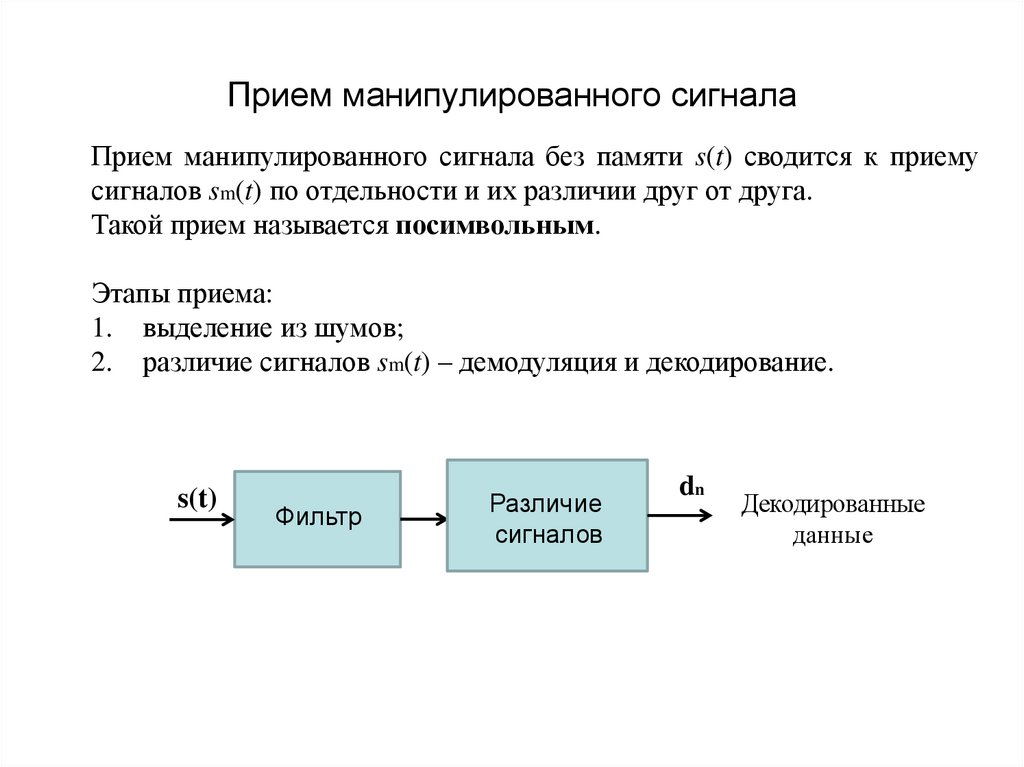
5. Прием манипулированного сигнала

Прием манипулированного сигнала без памяти s(t) сводится к приему
сигналов sm(t) по отдельности и их различии друг от друга.
Такой прием называется посимвольным.
Этапы приема:
1. выделение из шумов;
2. различие сигналов sm(t) – демодуляция и декодирование.
s(t)
Фильтр
Различие
сигналов
dn
Декодированные
данные

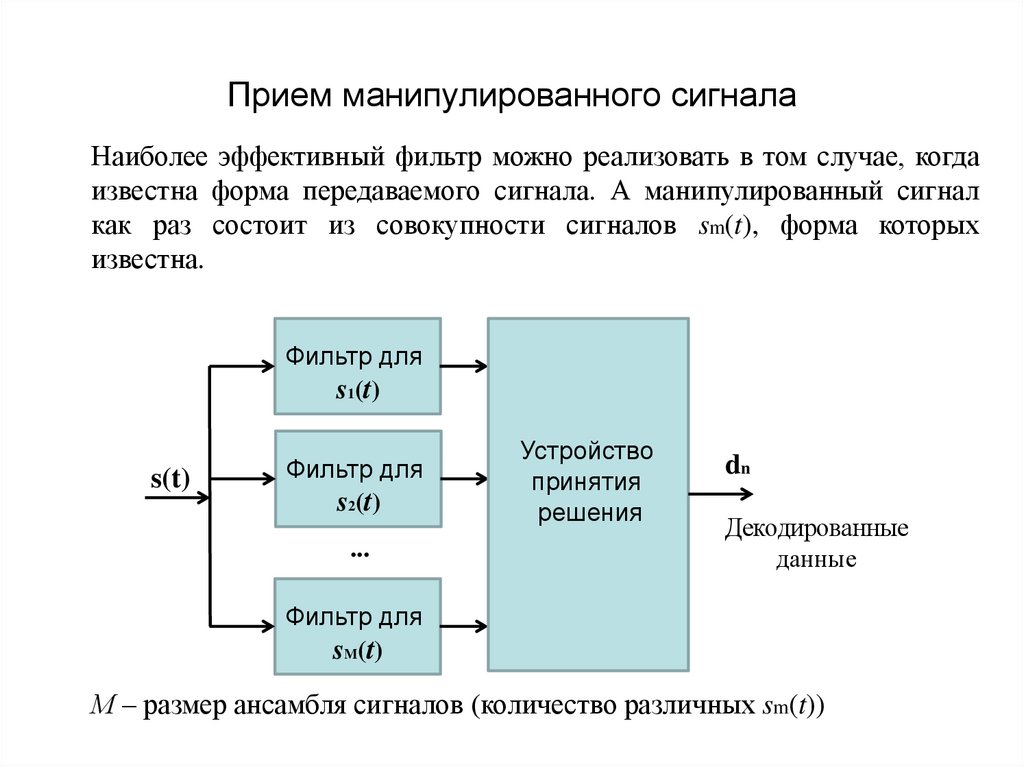
6. Прием манипулированного сигнала

Наиболее эффективный фильтр можно реализовать в том случае, когда
известна форма передаваемого сигнала. А манипулированный сигнал
как раз состоит из совокупности сигналов sm(t), форма которых
известна.
Фильтр для
s1(t)
s(t)
Фильтр для
s2(t)
...
Устройство
принятия
решения
dn
Декодированные
данные
Фильтр для
sM(t)
М – размер ансамбля сигналов (количество различных sm(t))

7. Согласованный фильтр

Согласованный фильтр — линейный оптимальный фильтр,
позволяющий получить максимальное отношение сигнал/шум на
выходе фильтра для сигналов известной формы.
Сигнал на выходе любого линейного фильтра, в том числе и
согласованного, определяется выражением:
y(t ) s(t ) * h(t ) s( )h(t )d
где s(t) – входной сигнал;
y(t) – выходной сигнал;
h(t) – импульсная характеристика фильтра;
* – операция свертки
s(t)
Согласованный
фильтр
h(t)
y(t)

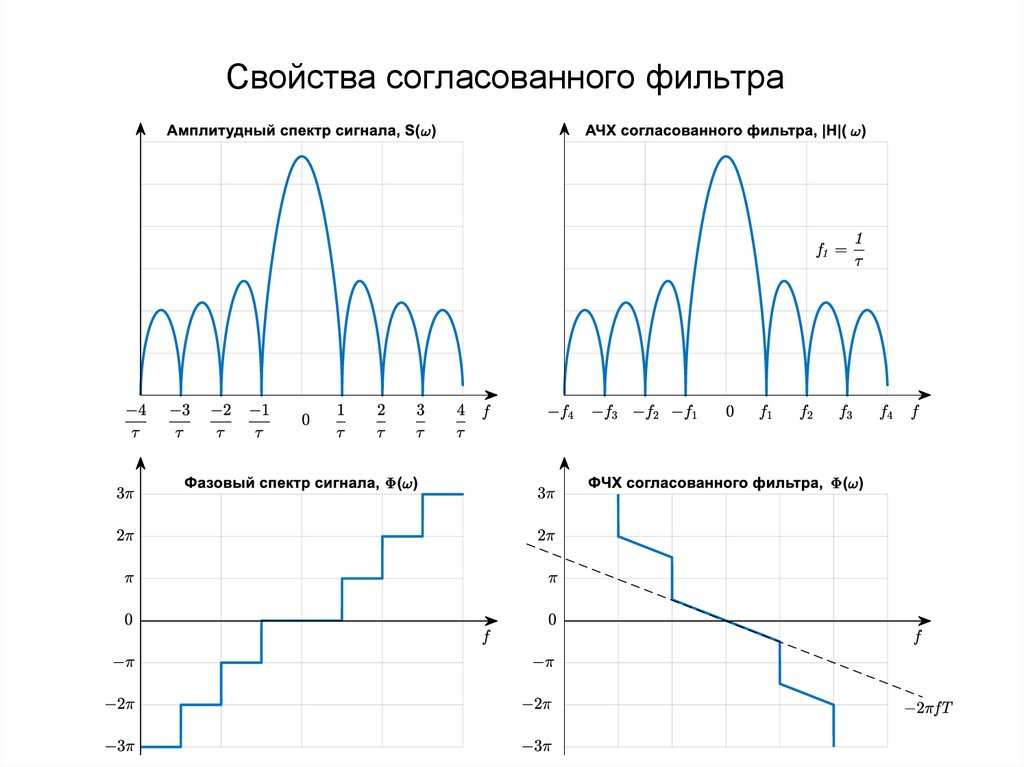
8. Свойства согласованного фильтра

Импульсная характеристика СФ имеет отзеркаленную форму
сигнала, для которого фильтр согласован:
h(t ) k s (TS t )
где Ts – длительность сигнала;
k – константа.
s(t)
Треугольный сигнал
h(t)
Импульсная характеристика СФ
t
t
Ts
Ts
h(t)
s(t)
t
t
Ts
Ts

9. Свойства согласованного фильтра

Комплексная частотная характеристика (она же АФЧХ) согласованного
фильтра комплексно сопряжена с Фурье-образом сигнала.
H( f ) k S * ( f )e i 2 Tf
где H(f) – частотная характеристика фильтра;
S(f) – Фурье-образ сигнала;
T – длительность сигнала;
k – константа.
i 2 Tf
e
Комплексная экспонента
говорит о сдвиге фаз, возникшем в
результате задержки сигнала в фильтре на время T.
АЧХ согласованного фильтра с точностью до постоянного коэффициента k
повторяет амплитудный спектр сигнала:
H( f ) k S ( f )
ФЧХ согласованного фильтра повторяет фазовый спектр сигнала с
обратным знаком и с учетом задержки:
СФ ( f ) 2 Tf S ( f )
где S ( f ) - фазовый спектр сигнала.

10. Свойства согласованного фильтра

11. Отклик согласованного фильтра

Отклик СФ на сигнал определяется сверткой импульсной
характеристики h(t) и сигналом s(t)
Сигнал, проходя через СФ, не сохраняет свою форму.

12. Отклик согласованного фильтра

Отклик СФ на сигнал определяется сверткой импульсной
характеристики h(t) и сигналом s(t)
Сигнал, проходя через СФ, не сохраняет свою форму.

13. Оптимальный приемник

sm (t ) sin t , 0 t TS
Согласованный
фильтр
r(t) =sm(t)+n(t)
h(t)
y(t)
Устройство
выборки
__/ __
t=kTs
h(t ) sin TS t , 0 t TS
y(kTs)
Устройство
принятия
решения
k=0, 1, 2, 3 …
d(kTs)

14.

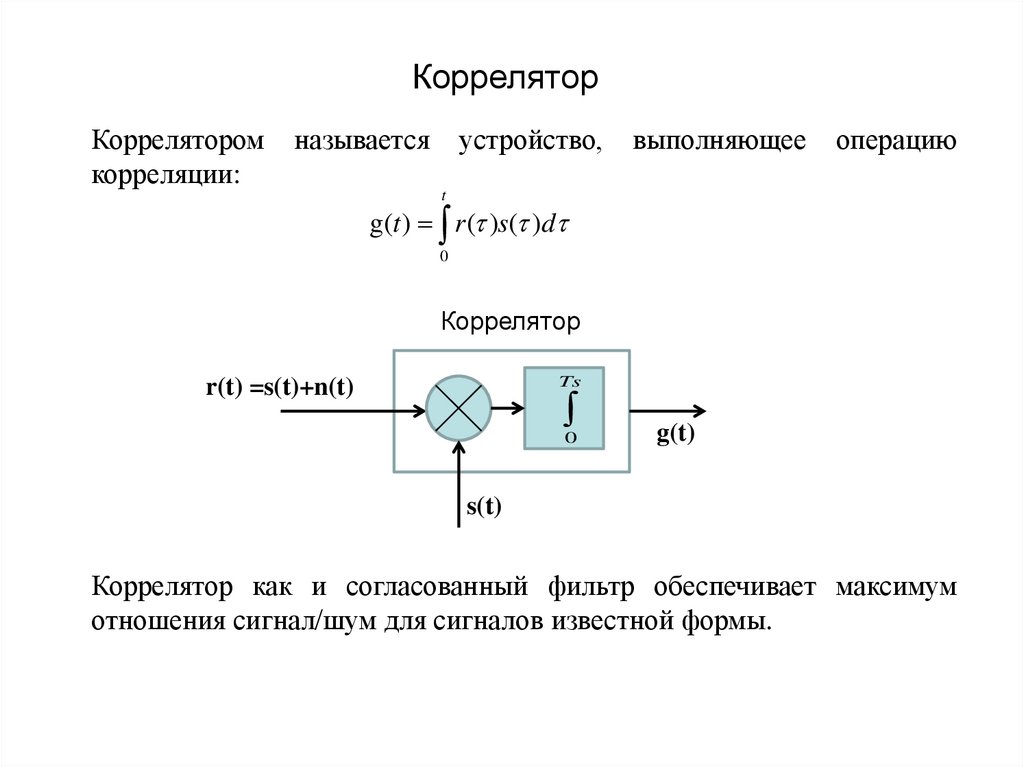
Коррелятор
Коррелятором
корреляции:
называется
устройство,
выполняющее
операцию
t
g(t ) r ( )s( )d
0
Коррелятор
Ts
r(t) =s(t)+n(t)
0
g(t)
s(t)
Коррелятор как и согласованный фильтр обеспечивает максимум
отношения сигнал/шум для сигналов известной формы.

15. Связь согласованного фильтра и коррелятора

Сигнал на выходе СФ выражается как:
t
y(t ) r (t ) * h(t ) r ( )h(t )d
0
t
t
0
0
y(t ) r ( )s TS (t ) d r ( )s(TS t )d
А в моменты времени t = Ts выражение можно переписать в
следующем виде:
y TS
TS
r ( )s( )d g TS
0
Данное выражение представляет собой выражение корреляции
сигналов r(t) и s(t). Из этой формулы следует очень важный вывод, о
том, что в момент времени t=Ts значение сигнала на выходе
согласованного фильтра равно значению сигнала на выходе
коррелятора.

16.

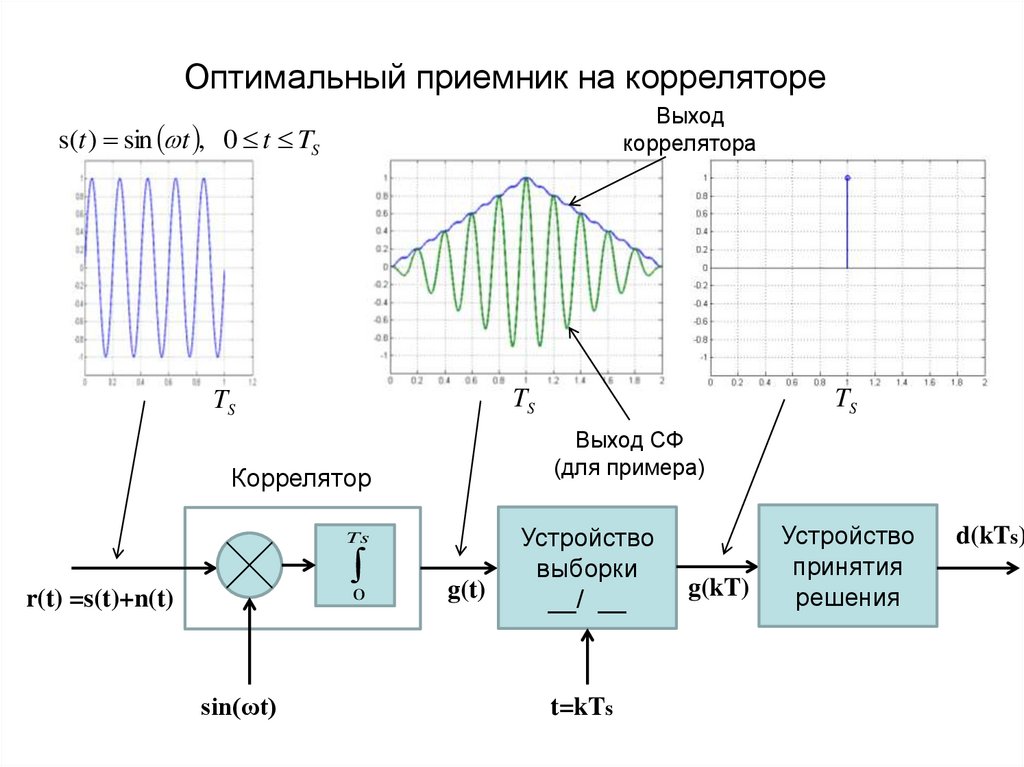
Оптимальный приемник на корреляторе
Выход
коррелятора
s(t ) sin t , 0 t TS
TS
TS
Выход СФ
(для примера)
Коррелятор
Ts
0
r(t) =s(t)+n(t)
sin(ωt)
TS
g(t)
Устройство
выборки
__/ __
t=kTs
g(kT)
Устройство
принятия
решения
d(kTs)

17. Когерентный и некогерентный прием

z(t ) A(t )ei 0t (t ) 0
Когерентным приемом называется прием, при котором начальная
фаза φо принимаемого сигнала известна.
Если начальная фаза φо не известна, то прием называется
некогерентным.
Со стороны приемника практически всегда начальная фаза
неизвестна, но она может быть восстановлена. Процесс
восстановления
начальной
фазы
φо называется
фазовой
синхронизацией.

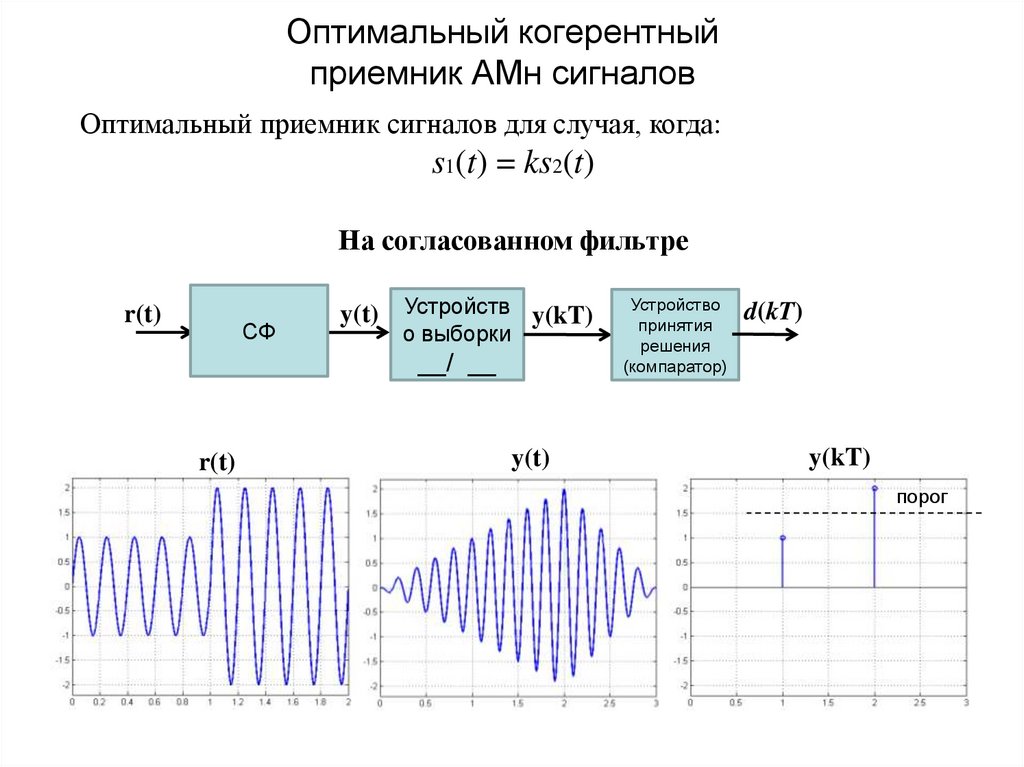
18. Оптимальный когерентный приемник АМн сигналов

Оптимальный приемник сигналов для случая, когда:
s1(t) = ks2(t)
На согласованном фильтре
r(t)
СФ
y(t) Устройств y(kT)
о выборки
__/ __
r(t)
y(t)
Устройство
принятия
решения
(компаратор)
d(kT)
y(kT)
порог

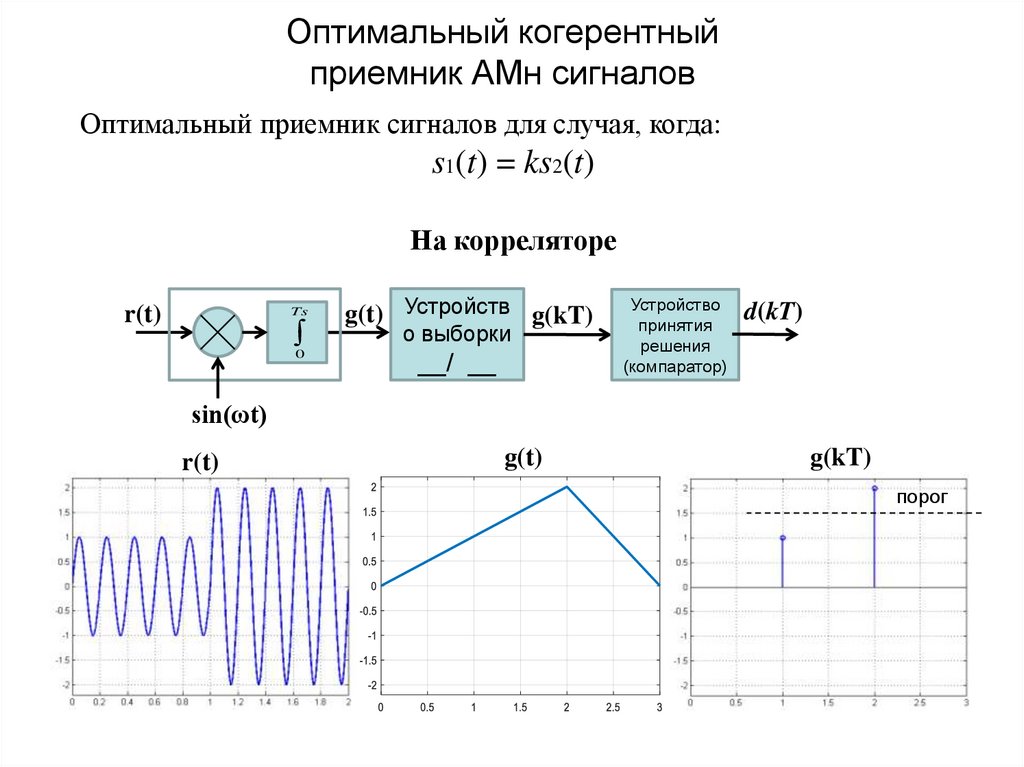
19. Оптимальный когерентный приемник АМн сигналов

Оптимальный приемник сигналов для случая, когда:
s1(t) = ks2(t)
На корреляторе
r(t)
Ts
0
g(t) Устройств g(kT)
о выборки
__/ __
Устройство
принятия
решения
(компаратор)
d(kT)
sin(ωt)
r(t)
g(t)
g(kT)
порог

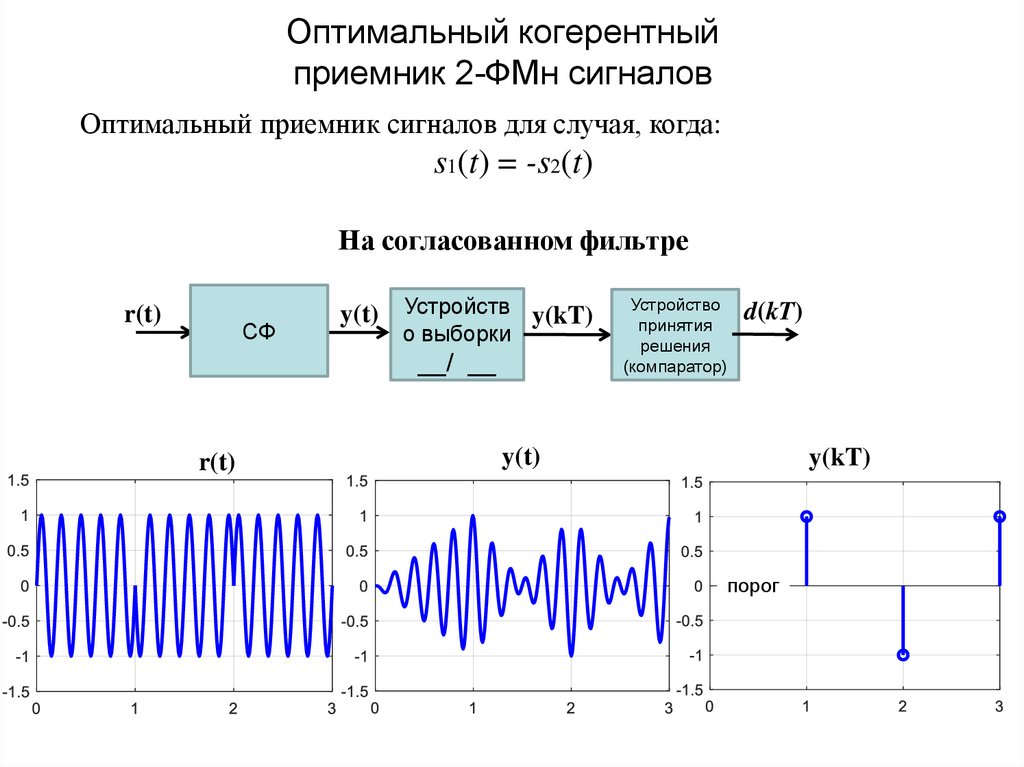
20. Оптимальный когерентный приемник 2-ФМн сигналов

Оптимальный приемник сигналов для случая, когда:
s1(t) = -s2(t)
На согласованном фильтре
r(t)
СФ
y(t) Устройств y(kT)
о выборки
__/ __
r(t)
Устройство
принятия
решения
(компаратор)
d(kT)
y(t)
y(kT)
порог

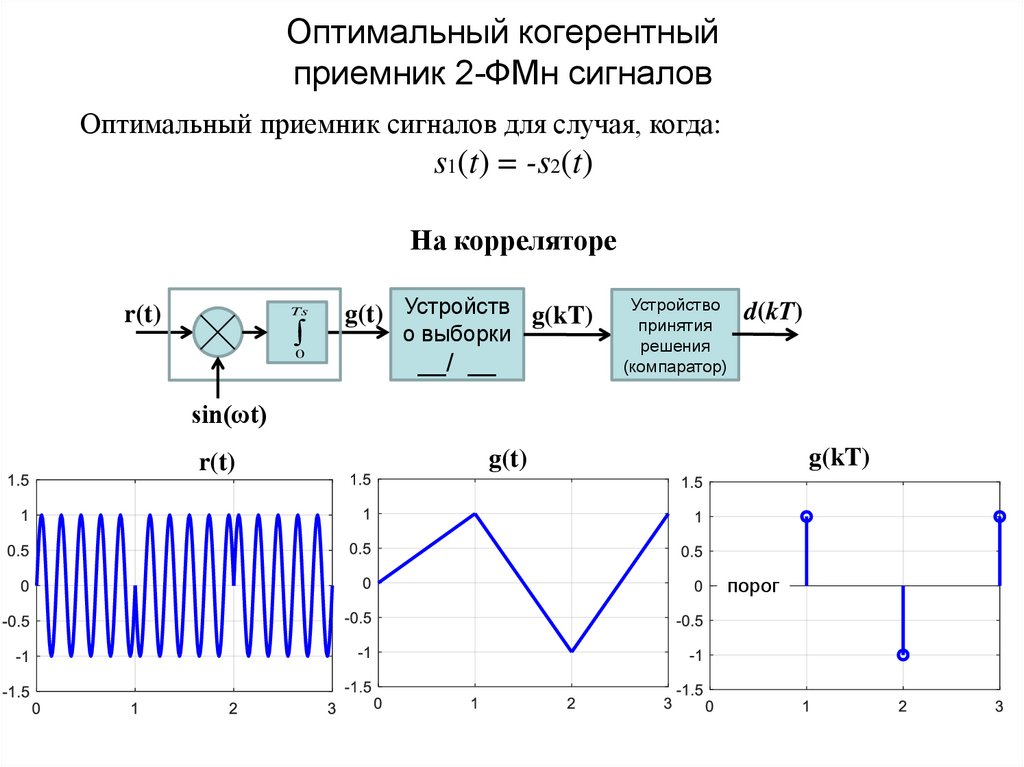
21. Оптимальный когерентный приемник 2-ФМн сигналов

Оптимальный приемник сигналов для случая, когда:
s1(t) = -s2(t)
На корреляторе
r(t)
Ts
0
g(t) Устройств g(kT)
о выборки
__/ __
Устройство
принятия
решения
(компаратор)
d(kT)
sin(ωt)
r(t)
g(kT)
g(t)
порог

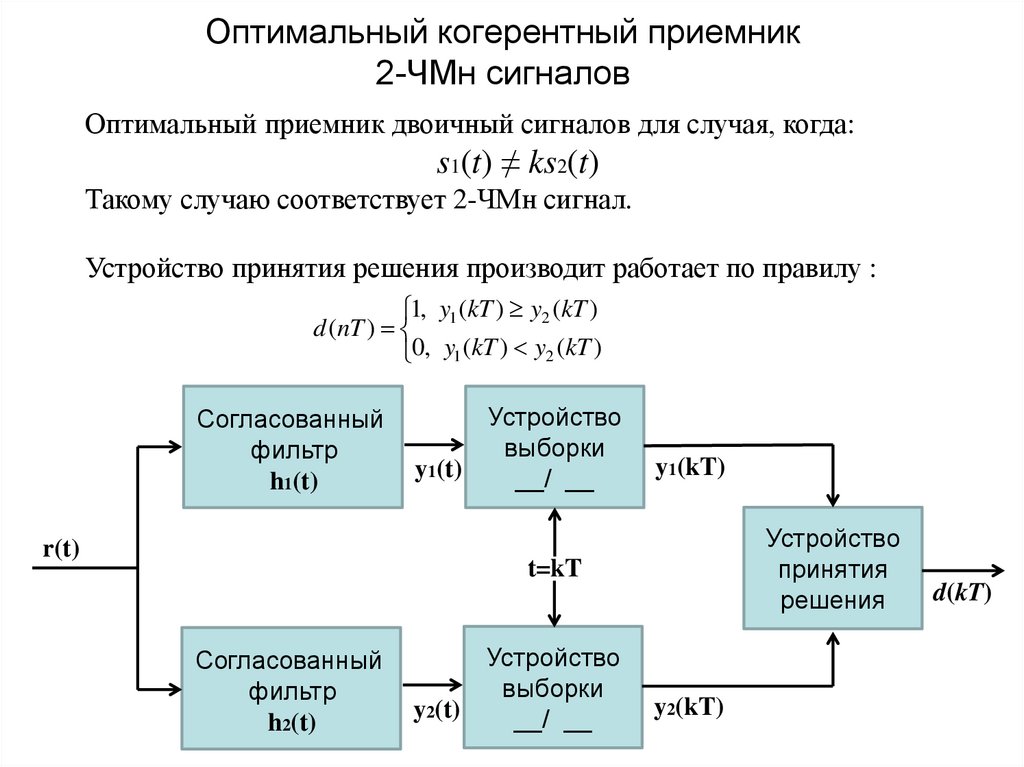
22. Оптимальный когерентный приемник 2-ЧМн сигналов

Оптимальный приемник двоичный сигналов для случая, когда:
s1(t) ≠ ks2(t)
Такому случаю соответствует 2-ЧМн сигнал.
Устройство принятия решения производит работает по правилу :
1, y1 (kT ) y2 (kT )
d (nT )
0, y1 (kT ) y2 (kT )
Согласованный
фильтр
h1(t)
r(t)
Устройство
выборки
y1(t)
__/ __
y1(kT)
Устройство
принятия
решения
t=kT
Согласованный
фильтр
h2(t)
Устройство
выборки
y2(t)
__/ __
y2(kT)
d(kT)

23. Оптимальный когерентный приемник 2-ЧМн

Коррелятор
Ts
0
r(t)
cos(ω1t)
Устройство
выборки
g1(t)
__/ __
g1(kT)
Устройство
принятия
решения
t=kT
Коррелятор
Ts
0
cos(ω2t)
Устройство
выборки
g2(t)
__/ __
g2(kT)
d(kT)

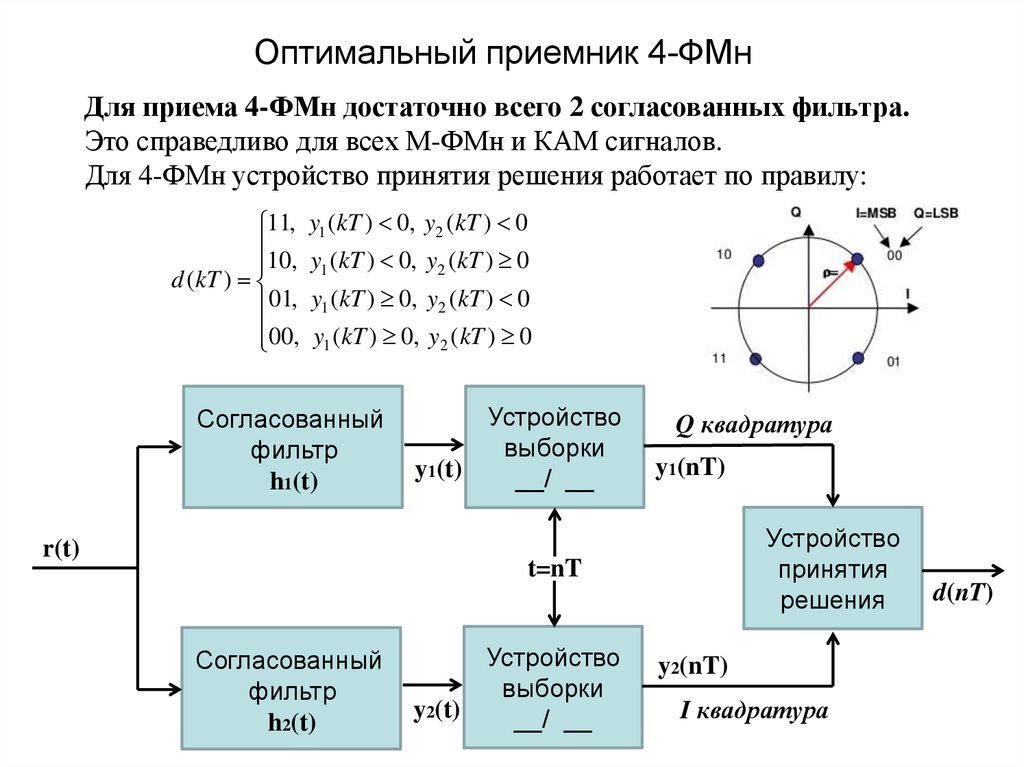
24. Оптимальный приемник 4-ФМн

Для приема 4-ФМн достаточно всего 2 согласованных фильтра.
Это справедливо для всех М-ФМн и КАМ сигналов.
Для 4-ФМн устройство принятия решения работает по правилу:
11,
10,
d ( kT )
01,
00,
y1 (kT ) 0, y2 ( kT ) 0
y1 (kT ) 0, y2 ( kT ) 0
y1 ( kT ) 0, y2 ( kT ) 0
y1 ( kT ) 0, y2 ( kT ) 0
Согласованный
фильтр
h1(t)
r(t)
Устройство
выборки
y1(t)
__/ __
Q квадратура
y1(nT)
Устройство
принятия
решения
t=nT
Согласованный
фильтр
h2(t)
Устройство
выборки
y2(t)
__/ __
y2(nT)
I квадратура
d(nT)

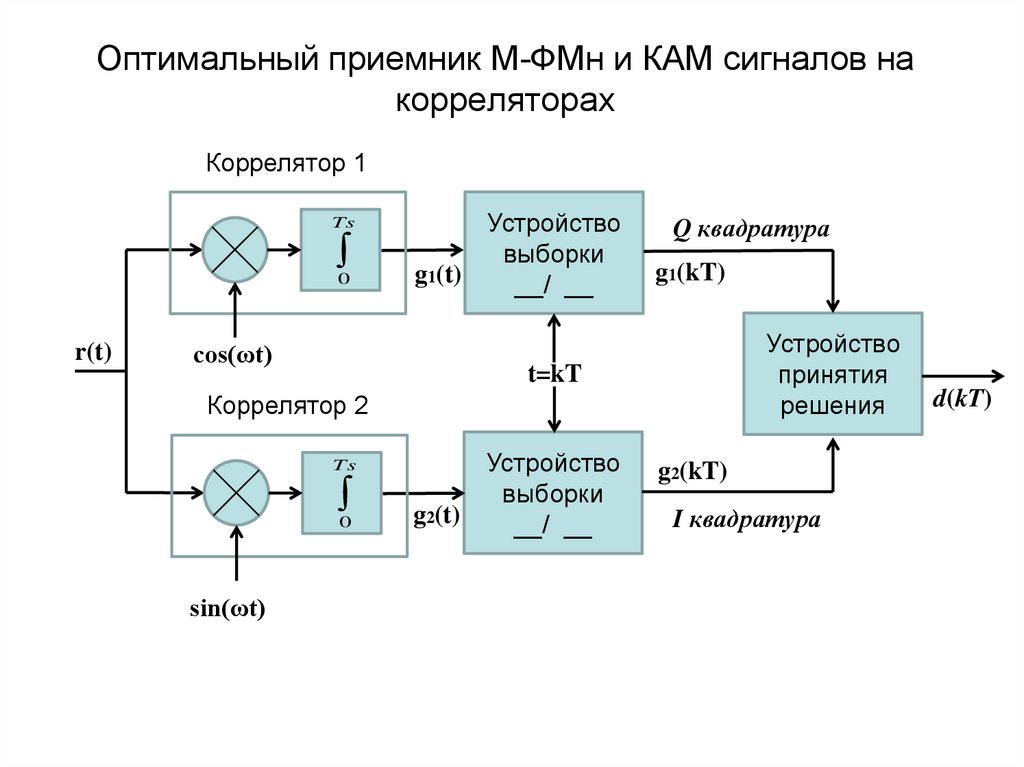
25. Оптимальный приемник М-ФМн и КАМ сигналов на корреляторах

Коррелятор 1
Ts
0
r(t)
cos(ωt)
Устройство
выборки
g1(t)
__/ __
Q квадратура
g1(kT)
Устройство
принятия
решения
t=kT
Коррелятор 2
Ts
0
sin(ωt)
Устройство
выборки
g2(t)
__/ __
g2(kT)
I квадратура
d(kT)

26. Оптимальный приемник M-ФМн и КАМ

Для М-ФМн и КАМ устройство принятия решения выбирает тот
символ, евклидово расстояние до которого минимально.
Евклидово расстояние
определяется через выражение:
em
y
I
d I ,m
y
2
Q
dQ ,m
Im d3
d1
2
em – евклидово расстояние до
m-го символа dm;
dI,m и dQ,m – проекция на оси I и
Q (координаты) m-го символа
dm;
yI и yQ – проекция на оси I и Q
(координаты) принятого
значения.
d2
yQ
d4
e3
e4
e8
e7
d5
d6
d7
d8
yI Re
d9
d10
d11
d12
d13
d14
d15
d16

27. Когерентный и некогерентный прием

Что будет если начальная фаза φо будет не такая, какую мы ожидаем?
Im
Im
φо
Re
Re

28.

Ортогональность сигналов
Сигналы s1(t) и s2(t) длительностью Тs называются ортогональными,
если их коэффициент корреляции равен нулю:
R
TS
s1 ( )s2 ( )d 0
0
Если на коррелятор или фильтр, согласованный с сигналом s1(t),
подать ортогональный сигнал s2(t) , то на выходе коррелятора или СФ
при t=Ts будет ноль.
s2 (t ) sin t , 0 t TS
s2(t)
Согласованный
фильтр
h1(t)
y(t)
Устройство
выборки
__/ __
y(kT)
Устройство
принятия
решения
d(kT)

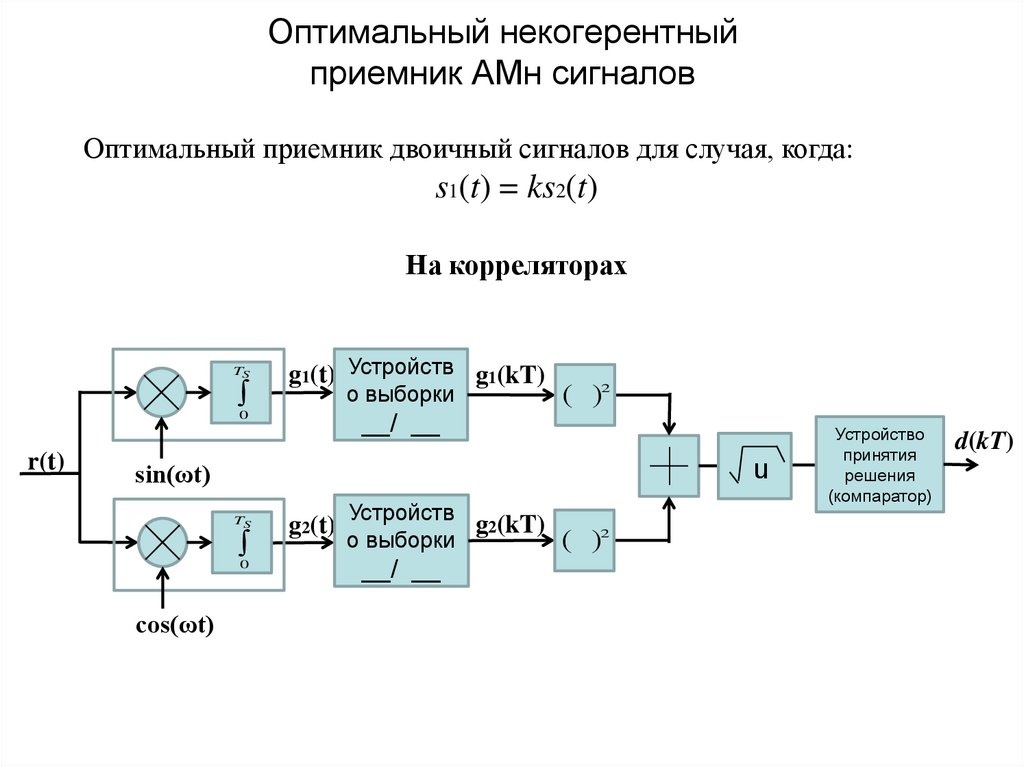
29. Оптимальный некогерентный приемник АМн сигналов

Оптимальный приемник двоичный сигналов для случая, когда:
s1(t) = ks2(t)
На корреляторах
TS
g1(t) Устройств g1(kT)
о выборки
0
r(t)
2
__/ __
u
sin(ωt)
TS
0
cos(ωt)
g2(t)
Устройств
g2(kT)
2
о выборки
__/ __
Устройство
принятия
решения
(компаратор)
d(kT)

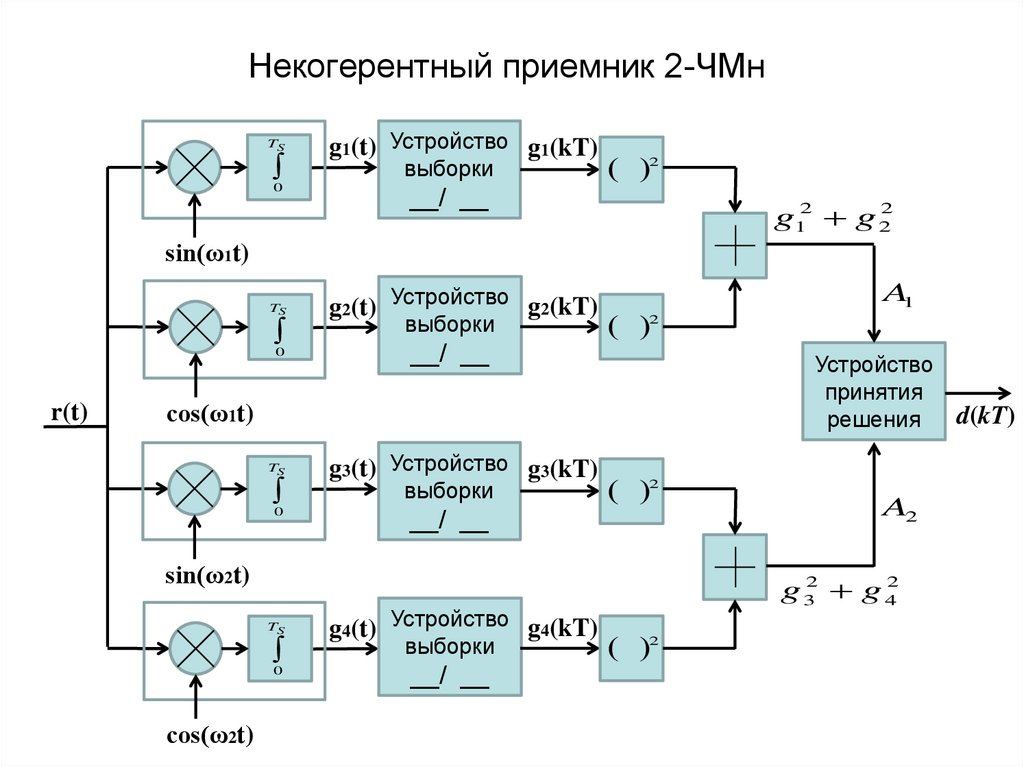
30. Некогерентный приемник 2-ЧМн

TS
0
g1(t) Устройство g1(kT)
выборки
2
__/ __
g12 g 22
sin(ω1t)
TS
0
r(t)
g2(t) Устройство g2(kT)
выборки
__/ __
Устройство
принятия
решения
cos(ω1t)
TS
0
g3(t) Устройство g3(kT)
выборки
2
__/ __
sin(ω2t)
TS
0
cos(ω2t)
g4(t) Устройство g4(kT)
выборки
__/ __
A1
2
A2
g 32 g 42
2
d(kT)

31.

Вероятность ошибки
Вероятность
ошибки
двоичных
определяется выражением:
равновероятных
сигналов
Eb (1 Rb )
Pb Q
N
0
где Rb – нормированный коэффициент взаимной корреляции:
T
1
Rb
s1 ( )s2 ( )d
Eb 0
Eb – энергия двоичного символа (бита):
T
T
Eb s1 (t ) dt s2 (t ) dt
0
2
2
0
Q(x) – Q-функция, определяется как: Q x
Для ортогональных сигналов Rb = 0, поэтому :
Eb
Pb Q
N
0
1
2
t 2 2
dt,
x e
x 0

32.

Вероятность ошибки
Для биполярного антиподного сигнала, для которого выполняется
условие s1(t)=-s2(t) коэффициент взаимной корреляции
Rb=-1,
следовательно вероятность ошибки будет определятся выражением:
2 Eb
Pb Q
N0
Для 2-ЧМн сигнала коэффициент взаимной корреляции зависит от
разницы частот между сигналами. При когерентном приеме
определяется через выражение:
Rb
sin 2 1 T sin 2 f 2 f1 T
2 1 T
2 f 2 f1 T
Коэффициент взаимной корреляции можно считать пренебрежимо
малой величиной при разности частот 2 1 T 2 при которой
|Rb|<0.07.

33.

Коэффициент взаимной корреляции для 2-ЧМн
при когерентном приеме
Встает вопрос, какая минимальная разность частот обеспечит нулевой
коэффициент корреляции при минимальной ширине спектра.
Легко заметить, что Rb=0 в значениях:
f 2 f1
n
2T
Минимальная разность при этом достигается при
f 2 f1
1
2T
2-ЧМн
для
которой
выполняется условие
f 2 f1
1
2T
называется модуляцией с
минимальным
сдвигом
(MSK).

34.

Вероятность ошибки
Rb=-1
Rb=0

35. Б. Скляр – Цифровая связь

Импульсная характеристика и свертка – стр. 61.
Согласованный фильтр – стр. 151.
Цифровой согласованный фильтр – стр. 211.
Связь свертки и корреляции – стр. 153.
Когерентный прием (детектирование) – стр. 210.
Когерентный прием М-ФМн – стр. 215.
Некогерентный прием – стр. 221.
Некогерентный прием ЧМн (FSK) – стр. 225