Логические основы компьютеров

1. Логические основы компьютеров

1
Логические основы
компьютеров
§ 18. Логика и компьютер
§ 19. Логические операции
§ 20. Диаграммы
§ 21. Упрощение логических выражений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

2. Логические основы компьютеров

2
Логические
основы
компьютеров
§ 18. Логика и компьютер
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

3. Логика, высказывания

Логические основы компьютеров, 10 класс
3
Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы,
доказывать утверждения.
Формальная логика отвлекается от
конкретного содержания, изучает только
истинность и ложность высказываний.
Аристотель
(384-322 до н.э.)
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
или ложно.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

4. Высказывание или нет?

Логические основы компьютеров, 10 класс
4
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

5. Логика и компьютер

Логические основы компьютеров, 10 класс
5
Логика и компьютер
Двоичное кодирование – все виды информации
кодируются с помощью 0 и 1.
Задача – разработать оптимальные правила
обработки таких данных.
Почему «логика»?
Результат выполнения операции можно
представить как истинность (1) или ложность (0)
некоторого высказывания.
Джордж Буль разработал основы алгебры,
в которой используются только 0 и 1
(алгебра логики, булева алгебра).
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

6. Логические основы компьютеров

6
Логические
основы
компьютеров
§ 19. Логические операции
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

7. Обозначение высказываний

Логические основы компьютеров, 10 класс
7
Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
!
}
простые высказывания
(элементарные)
Любое высказывание может быть ложно (0)
или истинно (1).
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если … то», «тогда и только тогда» и др.
AиB
A или не B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
если A, то B
Если сейчас идет дождь, то форточка открыта.
A тогда и только
тогда, когда B
Дождь идет тогда и только тогда, когда открыта
форточка.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

8. Операция НЕ (инверсия)

Логические основы компьютеров, 10 класс
8
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
также A , A ,
А
не А
0
1
1
0
not A (Паскаль),
! A (Си)
таблица
истинности
операции НЕ
Таблица истинности логического выражения Х – это
таблица, где в левой части записываются все
возможные комбинации значений исходных данных,
а в правой – значение выражения Х для каждой
комбинации.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

9. Операция И

Логические основы компьютеров, 10 класс
9
Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

10. Операция И (логическое умножение, конъюнкция)

Логические основы компьютеров, 10 класс
10
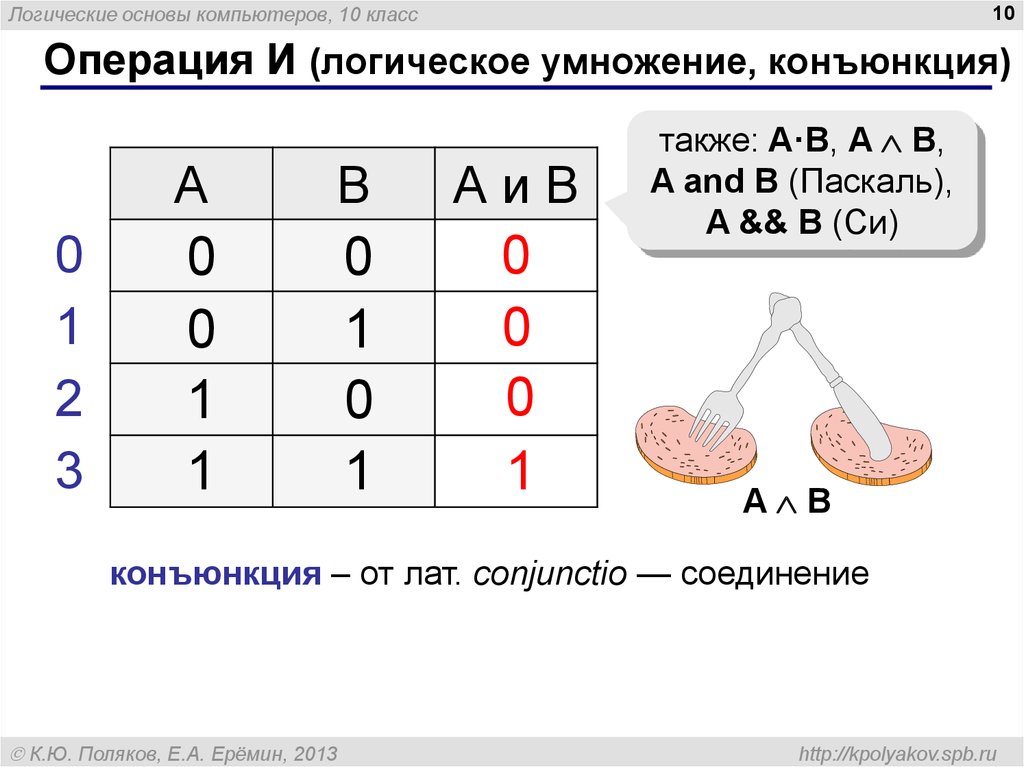
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также: A·B, A B,
A and B (Паскаль),
A && B (Си)
A B
конъюнкция – от лат. conjunctio — соединение
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

11. Операция ИЛИ (логическое сложение, дизъюнкция)

Логические основы компьютеров, 10 класс
11
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
истинно А или B, или оба вместе.
A или B
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

12. Операция ИЛИ (логическое сложение, дизъюнкция)

Логические основы компьютеров, 10 класс
12
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Паскаль),
A || B (Си)
дизъюнкция – от лат. disjunctio — разъединение
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

13. Операция «исключающее ИЛИ»

Логические основы компьютеров, 10 класс
13
Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (то есть A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
также:
A xor B (Паскаль),
A ^ B (Си)
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

14. Свойства операции «исключающее ИЛИ»

Логические основы компьютеров, 10 класс
14
Свойства операции «исключающее ИЛИ»
A A= 0
(A B) B = ?
A 0= A
A 1= A
A B A B A B
A
0
0
1
1
B
0
1
0
1
A B
К.Ю. Поляков, Е.А. Ерёмин, 2013
0
0
1
0
A B A B A B А B
0
1
0
0
0
1
1
0
0
1
1
0
http://kpolyakov.spb.ru

15. Импликация («если …, то …»)

Логические основы компьютеров, 10 класс
15
Импликация («если …, то …»)
Высказывание «A B» истинно, если не
исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
А B
1
1
0
1
A B A B
http://kpolyakov.spb.ru

16. Импликация («если …, то …»)

Логические основы компьютеров, 10 класс
16
Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит дома».
A – «Вася идет гулять».
A
B
А
B
B – «Маша сидит дома».
A B 1
?
А если Вася не идет
гулять?
0
0
1
1
0
1
0
1
1
1
0
1
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

17. Эквивалентность («тогда и только тогда, …»)

Логические основы компьютеров, 10 класс
17
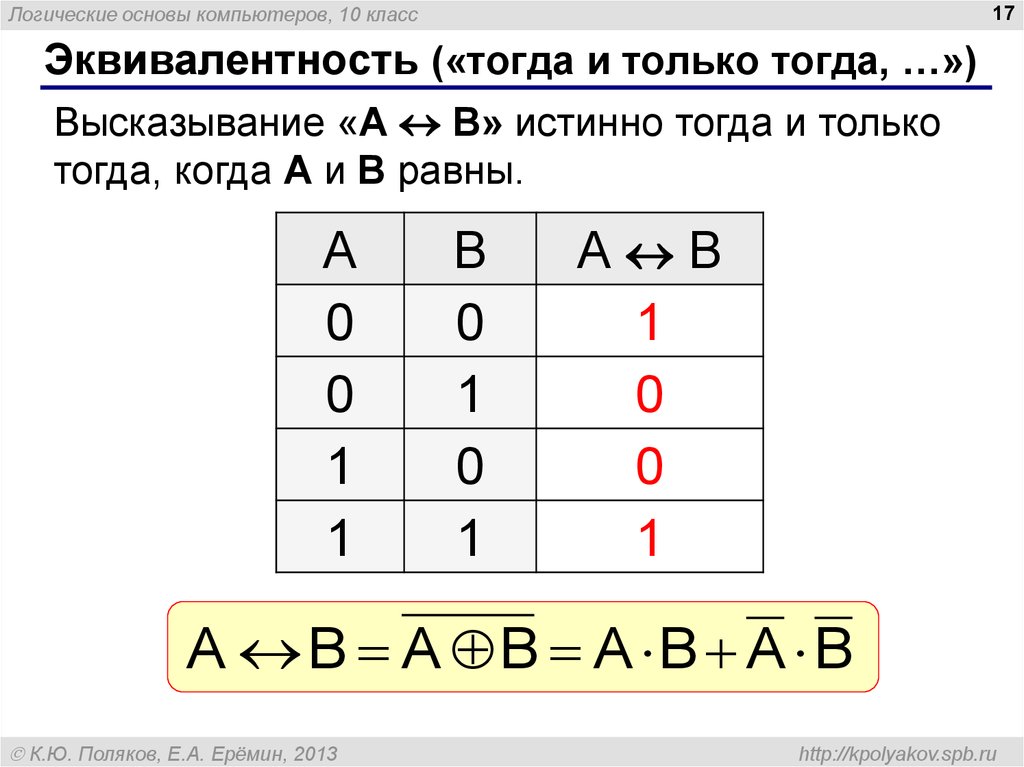
Эквивалентность («тогда и только тогда, …»)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
A B A B A B A B
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

18. Базовый набор операций

Логические основы компьютеров, 10 класс
18
Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно
реализовать любую логическую операцию.
И
ИЛИ
НЕ
базовый набор операций
?
Сколько всего существует логических операции
с двумя переменными?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

19. Вычисление логических выражений

Логические основы компьютеров, 10 класс
19
Вычисление логических выражений
1
4
2
5
3
X A B A C B C
+
Порядок вычислений:
•скобки
•НЕ
•И
•ИЛИ, исключающее ИЛИ
•импликация
•эквивалентность
A
К.Ю. Поляков, Е.А. Ерёмин, 2013
+
B
A
B
C
С
http://kpolyakov.spb.ru

20. Составление таблиц истинности

Логические основы компьютеров, 10 класс
20
Составление таблиц истинности
X A B A B B
0
1
2
3
A
B
A·B
A B
B
X
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
1
1
Логические выражения могут быть:
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

21. Составление таблиц истинности

Логические основы компьютеров, 10 класс
21
Составление таблиц истинности
X A B A C B C
0
1
2
3
4
5
6
7
A
B
C
A∙B
A∙C
B∙C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

22. Диаграммы Венна (круги Эйлера)

Логические основы компьютеров, 10 класс
22
Диаграммы Венна (круги Эйлера)
A
A
A
B
B
A·B
A
A+B
A
A
A
B
B
A B
К.Ю. Поляков, Е.А. Ерёмин, 2013
A B
B
A B
http://kpolyakov.spb.ru

23. Упрощение логических выражений

Логические основы компьютеров, 10 класс
23
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
A B A B A B
A B A B
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключения третьего.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

24. Упрощение логических выражений

Логические основы компьютеров, 10 класс
24
Упрощение логических выражений
Q M X H M X H (M M ) X H X H
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
К.Ю. Поляков, Е.А. Ерёмин, 2013
раскрыли
распределительный
исключения третьего
повторения
поглощения
http://kpolyakov.spb.ru

25. Логические элементы компьютера

Логические основы компьютеров, 10 класс
25
Логические элементы компьютера
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
A B
A B
1
ИЛИ
A
1
A B
B
И-НЕ
К.Ю. Поляков, Е.А. Ерёмин, 2013
ИЛИ-НЕ
http://kpolyakov.spb.ru

26. Логические элементы компьютера

Логические основы компьютеров, 10 класс
26
Логические элементы компьютера
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
A
A
ИЛИ:
B
A
&
& A B
A
A B A B
&
B
A B
&
A B
&
B
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

27. Составление схем

Логические основы компьютеров, 10 класс
27
Составление схем
последняя операция - ИЛИ
X A B A B C
И
A
B
A
B
&
A
B
& A B
A B
A B C
C
1
X
&
C
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

28. Конец фильма

Логические основы компьютеров, 10 класс
28
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

29. Источники иллюстраций

Логические основы компьютеров, 10 класс
29
Источники иллюстраций
1.
2.
3.
ru.wikipedia.org
иллюстрации художников издательства «Бином»
авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru