Похожие презентации:
Первое начало термодинамики. Работа. Внутренняя энергия. Теплота
1. 4. Первое начало термодинамики. Работа. Внутренняя энергия. Теплота.
2. Физические свойства макросистем, состоящих из большого количества частиц, изучаются взаимно дополняющими методами:
статистическими
термодинамическим.
Термодинамический
метод
основан
на
анализе
условий
и
количественных
соотношений при различных превращениях
энергии, происходящих в системе.
3.
Внутренняяэнергия
термодинамической
системы включает в себя кинетическую энергию
движения
частиц
(поступательного
и
вращательного
движения),
а
также
потенциальную энергию их взаимодействия.
4.
Видеальном
газе
пренебрегают
силами
межмолекулярного
взаимодействия,
поэтому
внутренняя энергия может быть принята как
сумма
кинетических
энергий
хаотического
движения всех молекул. В МКТ доказывается, что
в среднем на каждую степень поступательную и
вращательную степень свободы приходится
энергия
1
E kT ,
2
а на колебательную степень свободы энергия:
E kT .
5.
Таким образом внутренняя энергия идеальногогаза равна:
i
m
i
i m
U N kT
N A kT
RT
2
M
2
2M
где i – число степеней свободы молекулы.
Одноатомный газ – i=3,
Двухатомный газ – i=5,
Трехатомный газ – i=6.
6.
Изменение внутренней энергии газа связанос изменением температуры
i m
dU
RdT
2M
Изменение
внутренней
энергии
может
осуществляться
двумя
качественно
различными способами: путем совершения
работы и путем теплообмена.
7.
Элементарная работа, совершаемая газом приизменении его объема
dA pdV
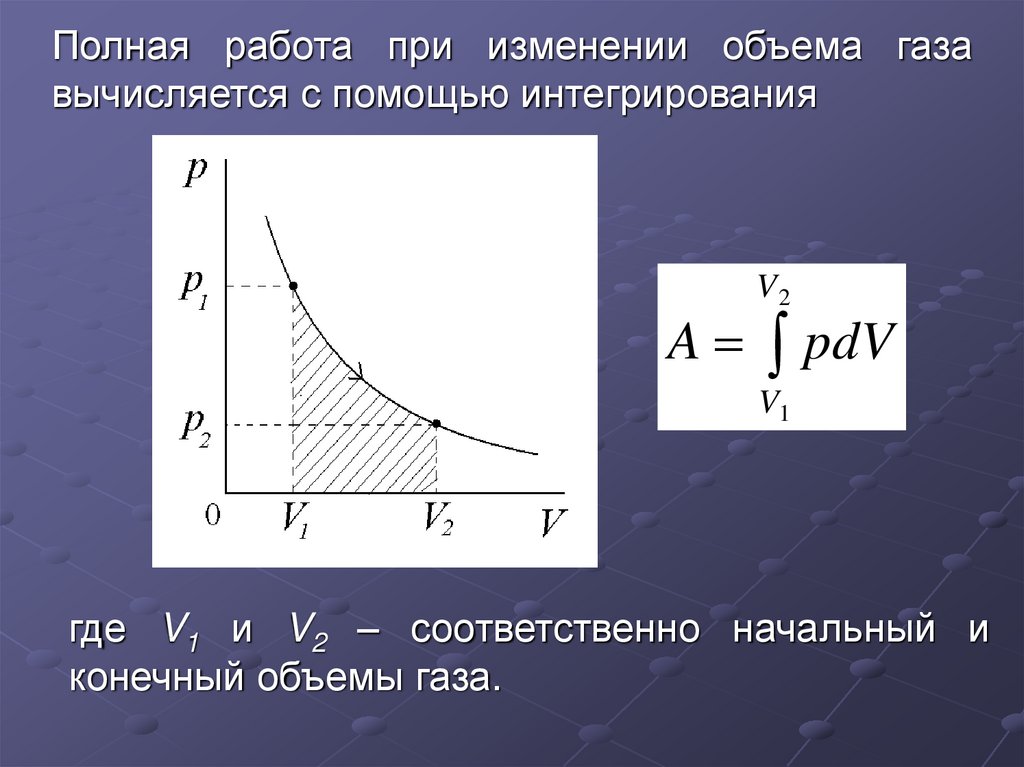
Полная работа при изменении объема газа
вычисляется с помощью интегрирования
A
V2
pdV
V1
где V1 и V2 – соответственно начальный и
конечный объемы газа.
8.
Полная работа при изменении объема газавычисляется с помощью интегрирования
A
V2
pdV
V1
где V1 и V2 – соответственно начальный и
конечный объемы газа.
9.
Количество теплоты, переданное системе,определяется по формуле
Q cm T
где с – удельная теплоемкость газа при
данном процессе.
Связь между молярной СМ
теплоемкостями газа
CM cM
где М – молярная масса газа.
и удельной с
10.
Первое начало термодинамики утверждает, чтоколичество теплоты Q, сообщаемое системе,
затрачивается
на
приращение
внутренней
энергии системы U и совершение системой
работы А над внешними телами:
Q U A
11.
Первоеначало
термодинамики
дифференциальной форме имеет вид
в
Q dU A
Отличия в записи малых величин отражают
тот факт, что внутренняя энергия является
функцией состояния системы, а работа и
теплота – функции процесса.
12.
В отличие от внутренней энергии системы,которая является однозначной функцией
состояния этой системы, понятия теплоты и
работы имеют смысл только в связи с
процессом изменения состояния системы. Они
являются энергетическими характеристиками
процесса изменения состояния системы.
13.
Первый закон термодинамики запрещаетсуществование вечного двигателя 1-го рода:
периодически
действующий
двигатель,
который совершал бы большую работу, чем
сообщенная ему извне энергия.
.
14.
5. Применение первого началатермодинамики к изопроцессам.
Зависимость теплоемкости
идеального газа от вида процесса
15.
Применим первое начало термодинамики кизопроцессам. Запишем закон в развернутом
виде:
cmdT dU pdV
16.
Так, при изохорном процессе dV=0, т.е. работаА=0 и вся теплота идет на изменение
внутренней энергии газа
cmdT dU
i m
dU
RdT
2M
17.
Откуда удельная теплоемкостьизохорном процессе:
газа
dU
i R
c cV
mdT 2 M
В других процессах объем газа изменяется.
при
18.
При изобарном процессе работа газа:A p V2 V1
m
A
R T2 T1
М
Изменение внутренней энергии
i
U p V
2
i m
U
R T
2M
19.
Количество теплотыi m
m
i 2 m
Q U p V
R T R T
R T
2M
М
2 М
Удельная теплоемкость газа при изобарном
процессе
Q
i 2 R
c cP
m T
2 M
20.
Молярные теплоемкости газа при постоянномобъеме и постоянном давлении связаны между
собой
CVM
i
R,
2
C pM
i 2
R
2
21.
Уравнение Майера связывает молярныетеплоемкости газа при изохорном и изобарном
процессах
C pM CVM R
22.
При изотермическом процессе температурагаза постоянна, поэтому количество теплоты
идет на совершение работы Q=A. Работа
вычисляется интегрированием
V2
A
V1
V2
pdV
V2
m RT
m
dV
RT ln
M V
M
V1
V1
или
p1
m
A RT ln
M
p2
23.
7. Адиабатный процесс.Политропный процесс.
24.
Адиабатный процесс реализуется в условияхтеплоизоляции системы, т.е. когда система не
обменивается энергией в форме теплоты с
другими системами. Следовательно
dA dU
25.
Получим соотношение между параметрамисостояния газа. Записывая выражения для
работы и изменения внутренней энергии
dA pdV
dU CV dT
i m
CV
R
2M
26.
pdV CV dTm RT
dV CV dT
M V
27.
Разделяем переменныеdT
mR dV
T
MCV V
mR C p CV
1
MCV
CV
Cp i 2
CV
i
28.
dTdV
1
T
V
Интегрируя, получаем
ln T ( 1) lnV const
ln T ( 1) lnV const
ln TV
1
const
29.
Таким образом, связь температуры и объемагаза при адиабатном процессе имеет вид
TV
1
const
30.
Поскольку при любом процессе для идеальногогаза
pV
const
T
Связь давления и объема при адиабатном
процессе
pV const
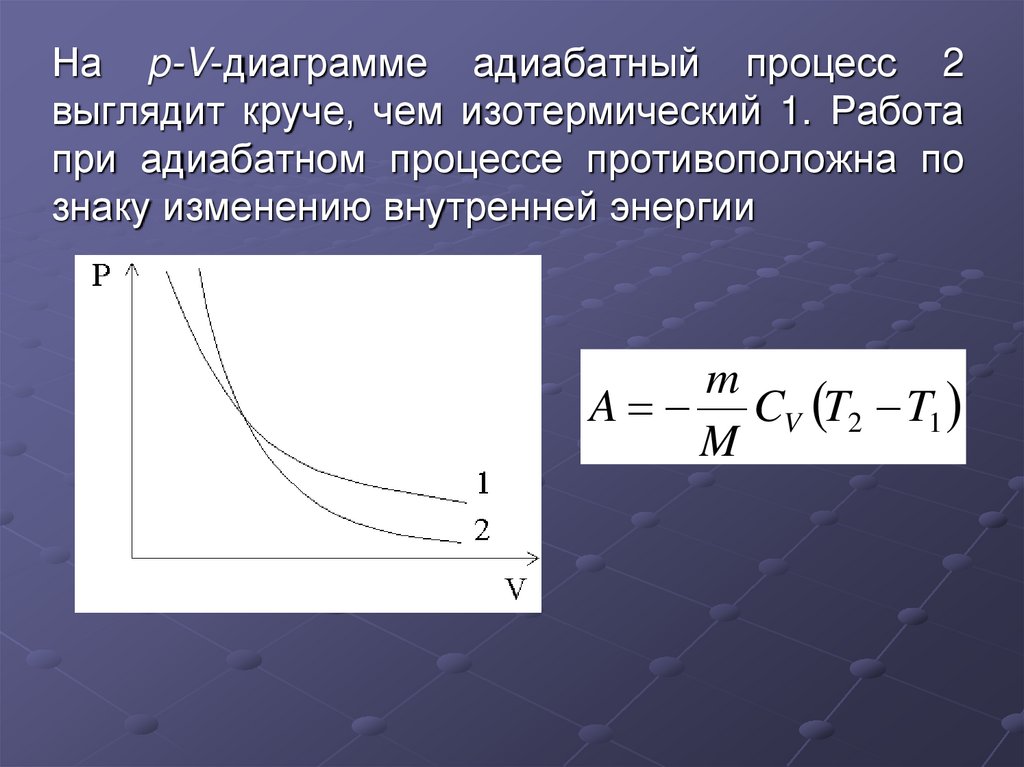
31. На p-V-диаграмме адиабатный процесс 2 выглядит круче, чем изотермический 1. Работа при адиабатном процессе противоположна по
знаку изменению внутренней энергииm
A CV T2 T1
M
32.
Политропными называются процессы, при которыхтеплоемкость тела остается постоянной. Для идеального
газа уравнение политропы имеет вид
pV const
n
n
C Cp
C CV
Рассмотренные ранее процессы относятся к категории
политропных. Изобарному процессу соответствует n=0,
изотермическому n=1, адиабатному n= .
33.
8. Обратимые и необратимые процессы.Круговой процесс (цикл). Цикл Карно.
34.
Для описания термодинамических процессоводного
первого
начала
термодинамики
недостаточно, поскольку оно не позволяет
определить направление протекания процесса.
35.
Термодинамическийпроцесс
называется
обратимым, если после него можно возвратить
систему в начальное состояние таким образом,
чтобы в других телах не осталось каких-либо
изменений.
Необходимое условие обратимого процесса –
его равновесность.
36.
Реальные процессы являются неравновесными, ипоэтому являются необратимыми.
37.
Круговым процессом называется термодинамическийпроцесс, в итоге которого система возвращается в
исходное состояние. Круговые процессы изображаются в
диаграммах p-V, p-T и др. в виде замкнутых кривых.
38.
Основные части тепловой машины: нагреватель,рабочее тело и холодильник.
Рабочее тело (обычно газ) получает количество теплоты
Q1 от нагревателя, совершает работу A за цикл, отдает
холодильнику количество теплоты Q2. Эффективность
тепловой
машины
определяется
термическим
коэффициентом полезного действия (кпд) для кругового
процесса (цикла)
Q2
A Q1 Q2
1
Q1
Q1
Q1
39.
Эффективность холодильнойхолодильным коэффициентом
Q2
Х
A
машины
определяется
40.
Среди всех круговых процессов наиболее эффективнымявляется процесс, составленный из четырех обратимых
процессов: двух изотерм и двух адиабат – цикл Карно
41.
Определим КПД данного цикла.V2
m
Q1 A12
RT1 ln
Участок 1-2: изотерма с Т1
M
V1
Участок 2-3: адиабата Q23 0 A23 U 23 CV T2 T1
Участок 3-4: изотерма с Т2
V4
m
Q2 A34
RT2 ln
M
V3
Участок 4-1: адиабата Q41 0 A41 U 41 CV T1 T2
,
42.
V2 mV4
m
RT1 ln
RT2 ln
M
V1 M
V3
V2
m
RT1 ln
M
V1
Температура и объем в состояниях 2-3 и 1-4 связаны:
1
1
T1V2 T2V3
1
1
T2V4 T1V1
43.
КПД цикла КарноT1 T2
T1
где Т1 – температура нагревателя; Т2
– температура холодильника.
В обратимом цикле Карно справедливо соотношение
Q1 Q2
T1 T2
44.
9. Энтропия. Второе начало термодинамики.Вычисление энтропии идеального газа.
45.
В отличие от количества теплоты Q, величинаQ/T (приведенная теплота) в обратимом
процессе
сохраняется
и
является
как
температура T и внутренняя энергия U функцией
состояния системы. Величину называют Q/T
энтропией S системы.
46. Энтропия – функция состояния системы, изменение которой в обратимом процессе равно отношению бесконечно малого количества
теплоты, сообщенного системе, кабсолютной температуре системы
dQ
dS
T
47.
Впроизвольном
необратимом
изменение энтропии системы
процессе
dQ
dS
T
т.е. изменение энтропии системы больше
величины Q/T , где T – температура внешнего
тела.
48.
dQТогда для любых процессов dS
,где знак
T
равенства относится к обратимым процессам,
а знак "больше" к необратимым.
49. Если система адиабатически изолирована (Q=0), то при любых процессах, происходящих в системе, энтропия системы не может
убывать, а значитdS 0
это утверждение является вторым началом
термодинамики.
Реальные процессы являются неравновесными, поэтому
энтропия системы может только возрастать, достигая
максимума
в
состоянии
термодинамического
равновесия.
50.
Изменение энтропии при равновесном переходесистемы из состояния 1 в состояние 2
вычисляется через интеграл
2
S12 S2 S1
1
2
dQ
T
dU dA
T
1
mRT
dQ dU dA CV dT
dV
MV
51.
Изменение энтропии при переходе из состоянияс параметрами T0, V0, конечное – T, V:
T
S
T0
V
CV dT
T
mR
dV
MV
V0
T m
V
S CV ln R ln
T0 M
V0
Энтропия, подобно внутренней энергии, – аддитивная
величина: энтропия системы равна сумме энтропий всех
тел, входящих в состав системы.
52.
Посколькувероятность
состояния
определяется
статистическим весом g, то между энтропией системы и
статистическим весом ее состояния существует связь,
которая описывается формулой Больцмана
S k ln g
Иными словами, второе начало термодинамики имеет
статистический характер, выражающий стремление
системы, состоящей из большого количества частиц, к
самопроизвольному переходу из состояний менее
вероятных в состояния более вероятные.


















































 Физика
Физика








