Бегущая волна, как решение нелинейного эволюционного уравнения с нелокальными членами

1. Бегущая волна как решение нелинейного эволюционного уравнения с нелокальными членами

Разработчик
Студент группы НП-401
Н.В.Байло
Руководитель
старший преподаватель кафедры
прикладной математики, к. ф.-м. н.
В.А.Попов

2.

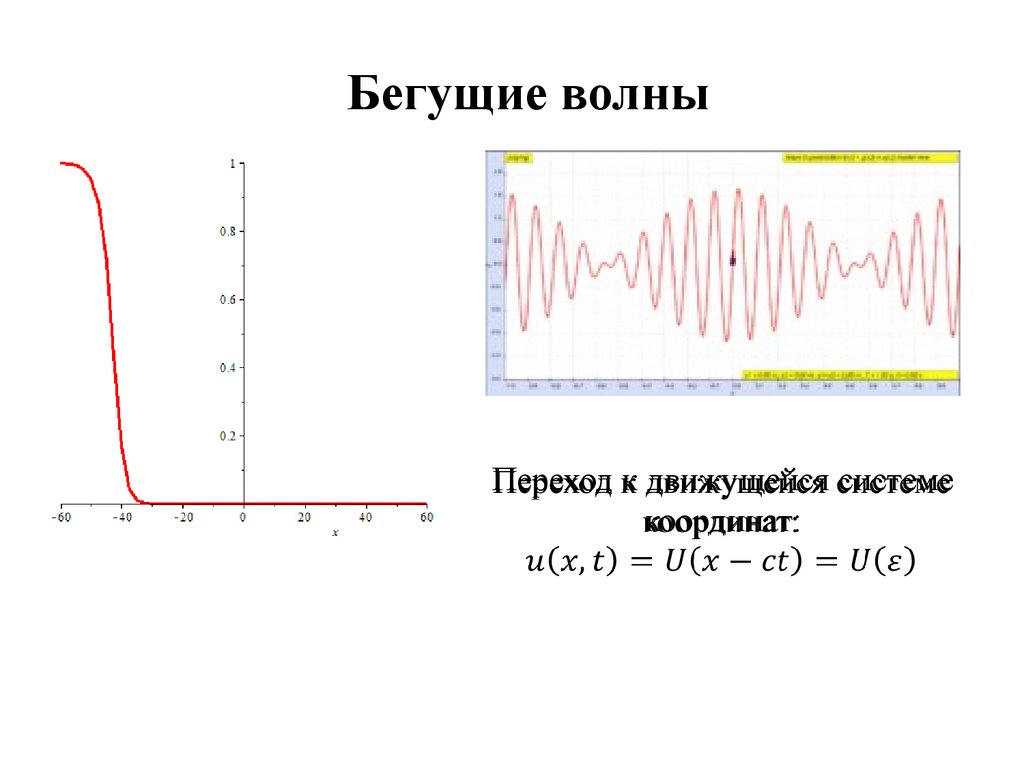
Бегущие волны
 
Переход к движущейся системе
координат:

3.

Уравнение реакции-диффузии
 
• Процесс эволюции биологического вида 
(уравнение Колмогорова-Пискунова –Петровского)
• Протекание химической реакции в 
автокаталитической фазе (Модель Шлёгеля, 
уравнение Семенова)
• Распространение нервного импульса 

4.

Модель Мальтуса
 
b-коэффициент рождаемости
d-коэффициент смертности
Решение уравнения :
Уравнение Колмогорова-Петровского-Пискунова
(КПП)
 
 
Эта задача имеет бесконечное множество решений
Минимальная скорость .

5.

Химическая модель Шлёгеля
 
 
k3
k1
¾¾
®
¾¾
®
A + 2 X ¬¾¾ 3 X , B ¬¾¾ X .
k2
k4
 П
Точное решение
.
Скорость волнового фронта

6.

Локальное уравнение Нагумо
 
где .
Cтационарные решения:
, устойчивые, неустойчивое.

7.

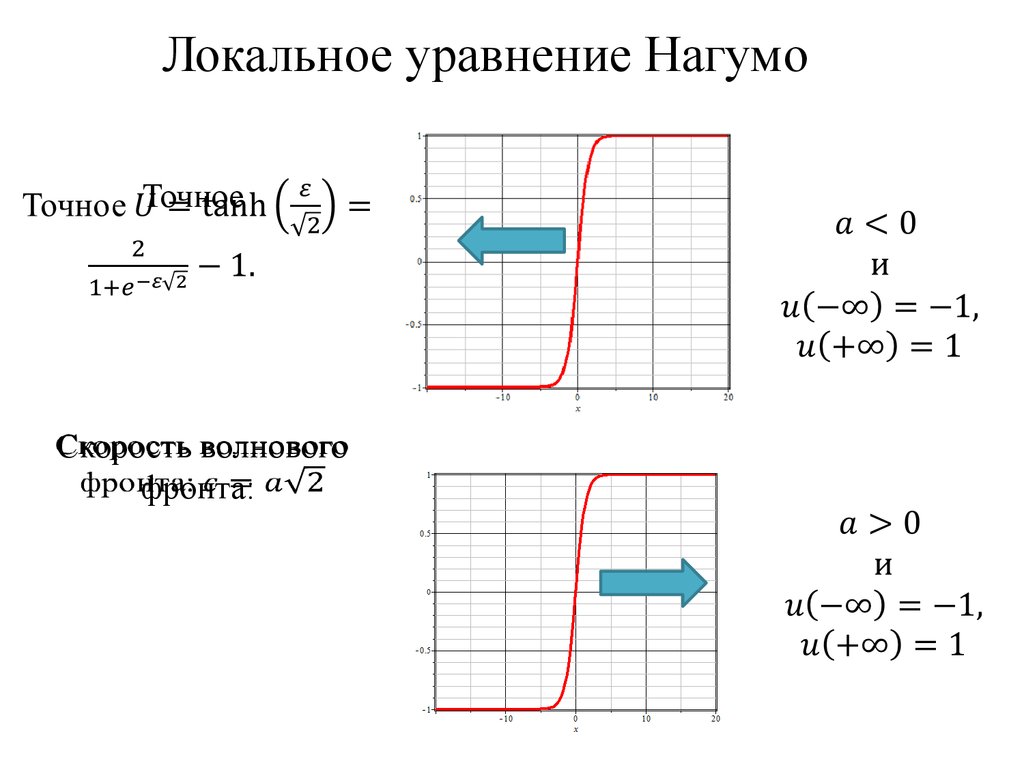
Локальное уравнение Нагумо
Точное
 
Скорость волнового
фронта:
 
 

8.

Нелокальное уравнение Нагумо
 
 
,

9.

 
Влияние нелокального члена на устойчивость
положений равновесия и
• Линеаризация около стационарного решения U*.
• Задача на собственные значения
• Знак действительной части собственного значения
 Для
получаем
получаем

10.

В переменных пространства и времени
 
Возмущение стационарного решения .
t= 0
 
t= 30
При 
 

11.

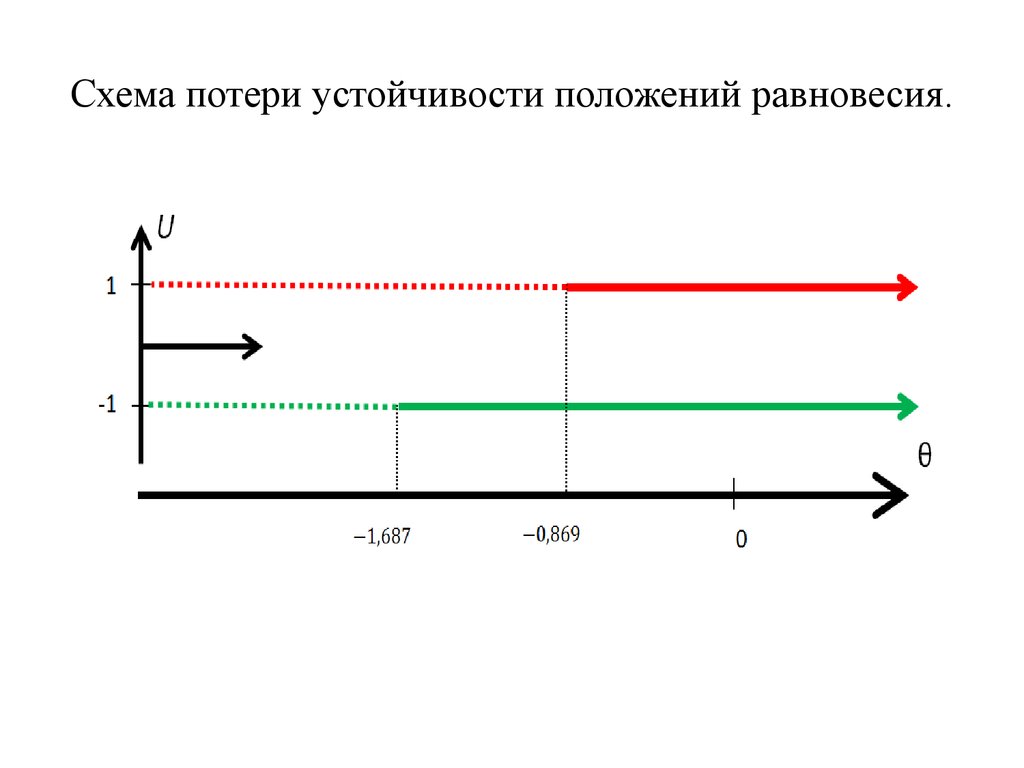
Схема потери устойчивости положений равновесия.

12.

 
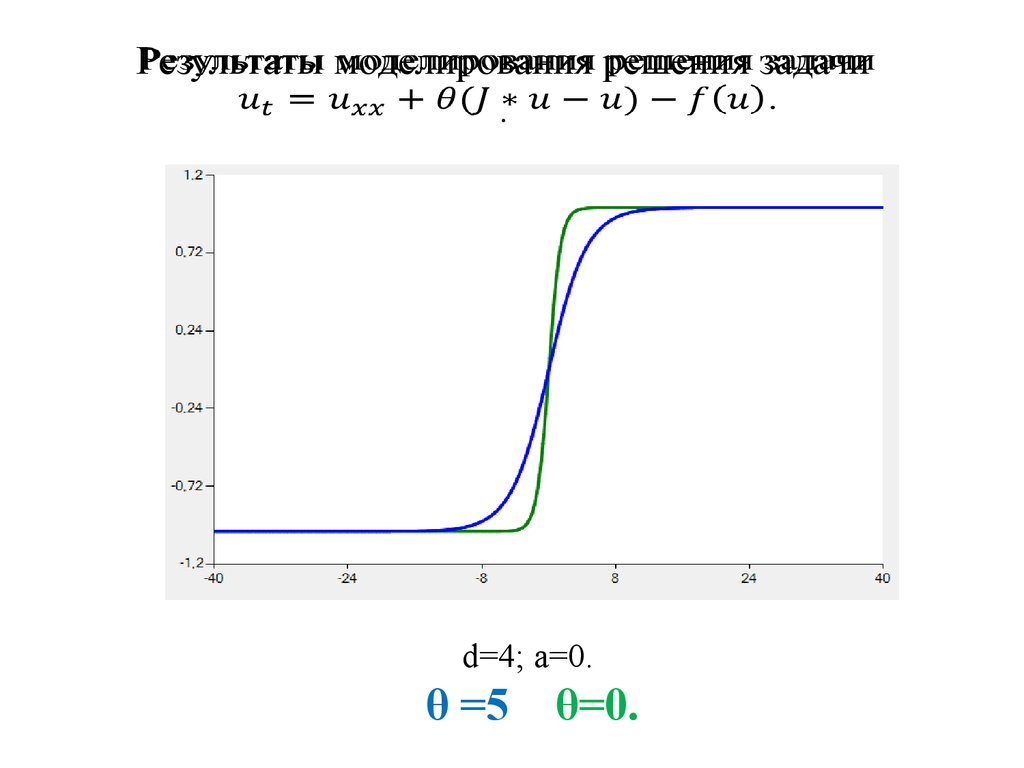
Результаты моделирования решения задачи 
.
d=4; a=0.
θ =5
θ=0.

13.

 
Результаты моделирования решения задачи 
.
d=4; a=0.
θ =5
θ=0.