Численное решение уравнений нелинейной оптики

Решение методом расщепления по физическим факторам

В случае уравнения с дифракцией для поля

Сложность алгоритмов вычисления преобразования Фурье

574.50K

Категории: $Математика$ Математика

Физика

Похожие презентации:

Численное решение систем нелинейных уравнений СНУ

Решение нелинейного уравнения. Тема 6

Решение нелинейного уравнения (тема 6)

Оптика

Лекция 3: Волновая оптика. Дифракция. Фурье оптика

Численное решение систем линейных алгебраических уравнений СЛАУ

Материальные уравнения линейной электродинамики

Численное решение систем линейных алгебраических уравнений (СЛАУ)

Нелинейная динамика. Лекция 4

Классическая оптика

Численное решение уравнений нелинейной оптики

1. Численное решение уравнений нелинейной оптики

2. Содержание

• Описание световых волн. Уравнения для
электромагнитных волн.
• Линейный режим взаимодействия света с
веществом.
• Нормировка динамических уравнений.
• Решение уравнений методом расщепления.
• Решение уравнений с учётом дифракции.
• Описание нелинейного режима
взаимодействия света с веществом.

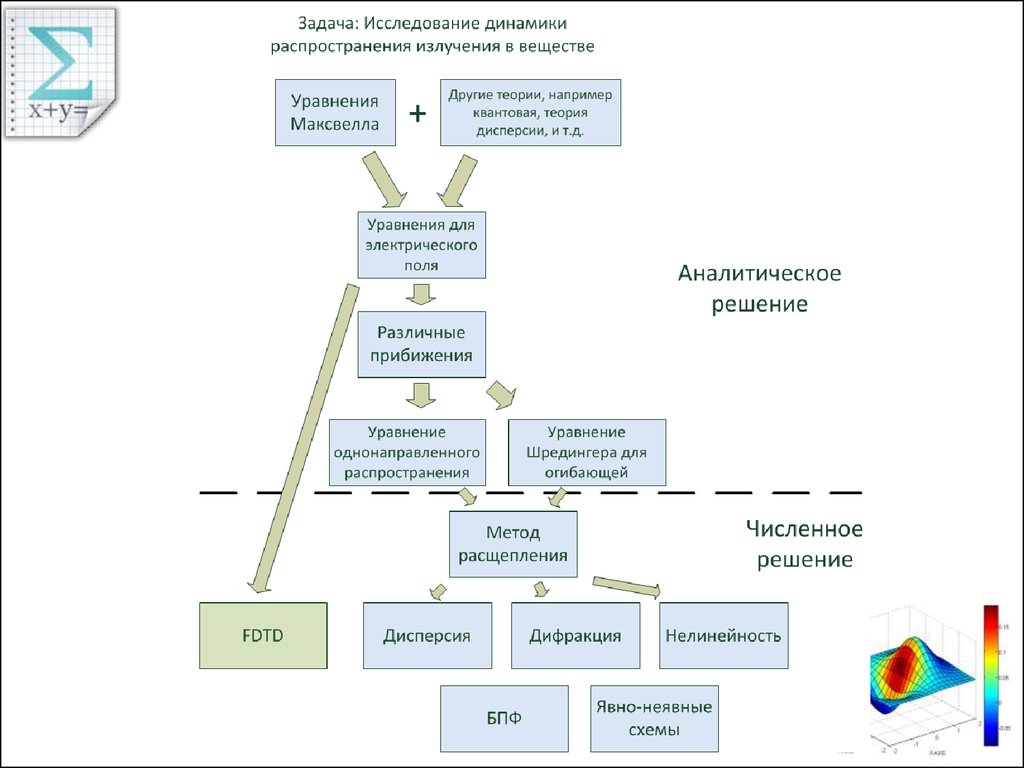
3. Цель решения уравнений

Современные оптические системы представляют
собой сложные комплексы из различных
оптических элементов, в каждом из которых
происходит взаимодействие оптического
излучения (или электромагнитного излучения
других диапазонов – например, терагерцового
диапазона) с различными материалами.
Необходимо иметь возможность предсказывать
как ведет себя оптическое излучение в
различных условиях, для этих целей все чаще
используется численное моделирование.

4. Электромагнитная природа света

В рамках электромагнитной теории все излучение
подчиняется законам Максвелла
D - электрическая индукция, B - магнитная индукция,
E - напряжённость электрического поля,
H - напряжённость магнитного поля,
j - плотность электрического тока,
r - плотность стороннего электрического заряда

5. Уравнения Максвелла

При решении оптических задач очень часто
отсутствуют свободные заряды и токи:
r 0
j 0
А также вместо индукции поля используют
поляризацию:
e0 , m0 – электрическая и магнитная постоянные,
для которых справедливо e0 m0 =1/c2
Большинство сред в оптике немагнитные, т.е.
M=0

6. Уравнения Максвелла

Получается система
e 0 E P 0
H 0
H
t
E P
H e0
t t
E -m 0
Применяя оператор ротора к третьему
уравнению системы и подставляя четвертое,
получаем волновое уравнение Максвелла

7. Волновое уравнение Максвелла

Для решения необходимо знать связь между P
иE–
материальные уравнения, они различны для
разных сред

8. Материальные уравнения

В самом общем виде линейная поляризация
зависит от прошлых значений поля в данной
точке (если отклик среды локальный)
PNL обычно является малым по отношению к PL и в
первом приближении им можно пренебречь

9. Содержание

• Описание световых волн. Уравнения для
электромагнитных волн.
• Линейный режим взаимодействия света
с веществом.
• Нормировка динамических уравнений.
• Решение уравнений методом расщепления.
• Решение уравнений с учётом дифракции.
• Описание нелинейного режима
взаимодействия света с веществом.

10. Линейный режим

Так как зависимость между PL и E
представляет собой свертку ее удобно
записывать в спектральном виде (после
применения преобразования Фурье
свертка превращается в произведение
функций)

11. Линейный режим

e(w) - Зависимость в общем случае
комплексная, она описывает как
дисперсию, так и поглощение, в случае
отсутствия поглощения e(w) n2(w)
В случае изотропной среды в линейном
приближении
Тогда

12. Вид скалярных уравнений

Уравнение Шредингера для огибающей
Очень часто a считают равным 0, а также
пренебрегают последними двумя слагаемыми
в этом уравнении, при этом надо учитывать
что дисперсия описана здесь описана в
следующем виде:
k (w ) k (w 0 )
1
1
1
(w - w 0 ) 2 (w - w 0 ) 2 3 (w - w 0 ) 3
V
2
6

13.

Вид скалярных уравнений
Уравнение для поля импульса с использованием
приближения однонаправленного распространения
(без учета дифракции, т.е. в оптическом волокне)
E N 0 E
3E
2 E
a
b
Ed
gE
0
3
z
c t
t
t
-
t
при этом дисперсия задана в виде
k (w )
N0
b
w aw 3 c
w

14. Вид скалярных уравнений

Уравнение для поля импульса с использованием
приближения однонаправленного распространения
(с учетом дифракции)
E N 0 E
3E
E
c
- a 3 b Edt gE 2
Edt
z
c t
t
t
2N0
-
-
t
t
Здесь E уже зависит от трех координат и времени
2
2
2 2
x y
- Поперечный лапласиан

15. Содержание

16. Нормировка уравнения

t-
N0
z
c
или
t-
1
z
V
E
3E
c
2 E
- a 3 b Edt gE
Edt
z
2 N 0
-
-
E ~
x
y
E~
; w0 ~; ~
x ; ~
y ;~
z aw03 z
E0
r
r
E 3 E
2 E
- 3 B Edt GE
D Edt
z
-
-

17. Отступление про вычислительную точность

Дробные числа в памяти компьютера могут иметь
одинарную, либо двойную точность
Одинарная точность – 4 байта – минимальное
положительное число имеет порядок 10-38,
максимальное: 1038 при этом хранятся около 7
значащих цифр.
Двойная точность – 8 байт – минимальное
положительное число имеет порядок 10-308,
максимальное: 10308, при этом хранятся около 15
значащих цифр

18. Отступление про вычислительную точность

При этом надо помнить, что для
компьютера
после вычисления
a=1
a = a + 10-20
a будет равно по прежнему 1

19. 20. Содержание

21. Решение методом расщепления по физическим факторам

F
( Dˆ disp Dˆ diff Nˆ ) F
z
Метод расщепления состоит в последовательном
решении
F
Ddisp F ,
z
F
Ddiff F ,
z
F
NF ,
z

22. В случае уравнения с дифракцией для поля

N 0 E
E
3E
a 3 - b Edt
z
c t
t
-
t
E
c
Edt
z 2 N 0
-
t
E
2 E
- gE
z
t

23. Дисперсионное уравнение

N 0 E
E
3E
a 3 - b Edt
z
c t
t
-
t
Данное уравнение может быть переписано в
спектральной области (применяя преобразование
Фурье к каждой из частей) и используя
F
Ф (iw ) Ф{F }
t
t
Ф Fdt ' (iw ) -1 Ф{F }
-

24. Дисперсионное уравнение

G N 0
b
(iw ) a(iw ) 3 - G
z c
iw
Либо в более общем виде
w
ˆ
Ddisp -i n(w )
c
Можно заменить производную по z конечной
разностью (апроксимация первого порядка по z)
Получим
G Gz z - Gz
z
z
Gz z Gz zDˆ dispGz

25. Решение дисперсионного уравнения

Однако такое уравнение имеет точное
решение
Gz z Gz exp( -i znwn(w ) / c)

26. Решение дисперсионного уравнения

Таким образом для решения дисперсионного
уравнения необходимо
• посчитать спектр поля
• умножить спектр на экспоненту от дисперсионной
функции
• посчитать обратный спектр
Можно использовать алгоритм БПФ

27. Про преобразование Фурье

В случае когда сигнал у нас задан на сетке в виде
отсчетов sk справедлива следующая формула
Для того чтобы посчитать эти коэффициенты в
общем случае требуется O(n2) операций

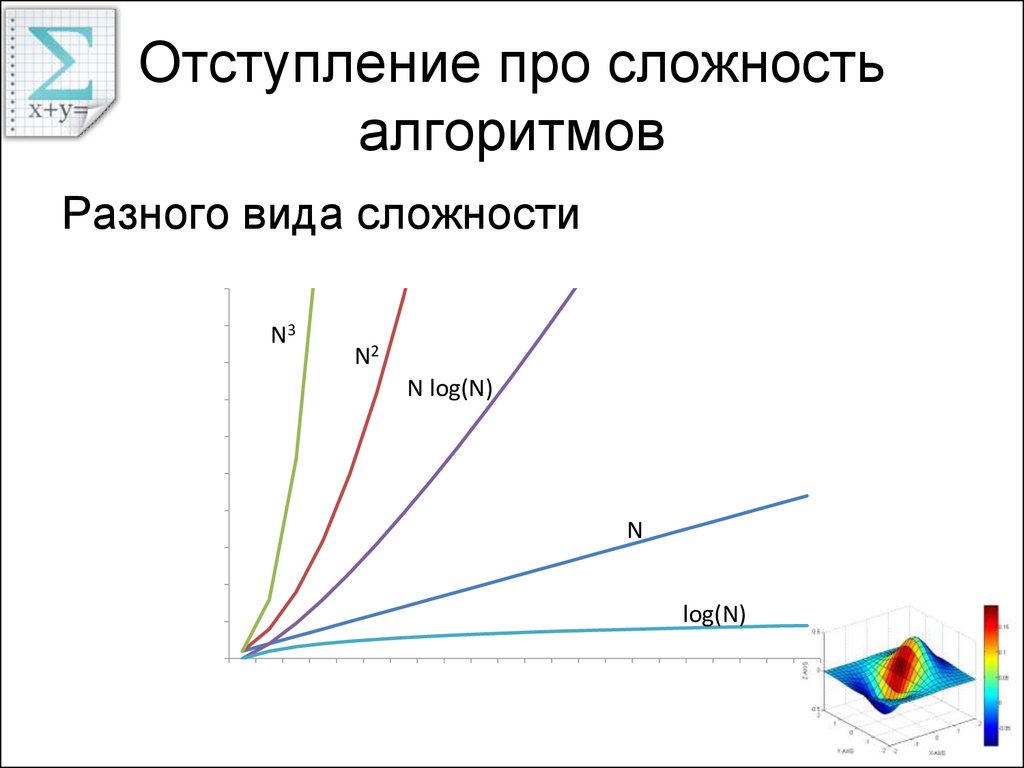
28. Отступление про сложность алгоритмов

Определение f(n)=O(g(n))
В нашем случае f(n) – количество операций
необходимых для расчета спектра сигнала из n
отсчетов, а g(n)=n2
В общем случае для произвольного алгоритма
расчет g(n) – сложная задача

29. Сложность алгоритмов вычисления преобразования Фурье

Для ДПФ необходимо O(n2) операций, где
n – размер массива входных данных,
т.е. количество отсчетов.
Для БПФ необходимо O(n log(n))
операций.
log 10 N
log
N
Так как
т.е., например
2
log 2
10
Основание алгоритма становится неважно

30. Отступление про сложность алгоритмов

Разного вида сложности
N3
N2
N log(N)
N
log(N)

31. БПФ

Ограничения накладываемые на
данные из-за использования БПФ
1) Равномерная сетка, т.е. ti+1-ti = t
2) Количество отсчетов равно степени
2: т.е.
N=2,4,8,16,32,64,…,1024,2048,4096,…

32. Содержание

33. Решение дифракционного уравнения

E
c
Edt
z 2 N 0
-
t
Переходим в спектральную область
G (w , x, y, z )
c
G (w , x, y, z )
z
2 N 0 (iw )
2G 2G
G 2 2
x
y

34. Память и время работы

Предположим G у нас зависит от 3 координат и
времени, тогда если мы ведем расчет используя z
как координату распространения нам необходимо
для каждого значения z иметь функцию G(t,x,y).
Предположим у нас сетка t от 1 до 1024, x от 1 до
1024, y от 1 до 1024, тогда Gt,x,y займет в памяти
компьютера 1024 x 1024 x 1024 ячейки (16 Гб), а для
расчета спектра понадобится
С · 1024 · 1024 · 1024 · log (1024)
операций

35. Скорость работы компьютера

Одна из характеристик процессоров –
тактовая частота, например 3 ГГц, т.е.
3 000 000 000 тактов в секунду.
Для элементарной операции нужно от
одного до нескольких десятков тактов.

36. Скорость работы компьютера

Факты влияющие на скорость
1)Тактовая частота
2)Реализация алгоритма
3)Количество тактов на операцию
4)Наличие конвейеров
5)Медленная работа с памятью
6)Наличие кэша
7)Параллелизация алгоритма

37. Время работы

Таким образом получается значение в
районе 300 секунд на шаг алгоритма

38. Решение дифракционного уравнения

Предположим, что импульс имеет осевую
симметрию, т.е. E(t, r, z), G(w, r, z), где
r x2 y 2
тогда Gt,r займет в памяти компьютера 1024 x 1024
ячеек, а процесс вычисления займет
C x 1024 x 1024 x log (1024)
1
(r )
r r r
G(w, r , z )
c
1
r G(w, r , z )
z
2 N 0 (iw ) r r r

39. Решение дифракционного уравнения

Gj
Gj 1
rj Gj -1
rj 1
1
2
2
( rj rj 1 ) rj 1
r j rj
r j
G j
1 G j 1 - G j
- 2
rj rj 1
rj
Сетка по r не обязана быть равномерной!

40. Решение дифракционного уравнения

.
Решение дифракционного
уравнения
схема Кранка-Николсона
Gin, j 1 - Gin, j
zn
(
)
0.5Dˆ diff Gin, j 1 Gin, j O([ z n ]2 ) i , j

41. Схема Кранка-Николсона

42. Содержание

43. Материальные уравнения

В самом общем виде линейная поляризация
зависит от прошлых значений поля в данной
точке (если отклик среды локальный)
PNL уже не является малым по отношению к PL

44. Решение нелинейного уравнения

E
2 E
- gE
z
t
1) Для вычисления производной можно
использовать БПФ, а можно центральную
разность
2) Для шага по z может также использоваться схема
Кранка-Николсона, однако так как уравнение
нелинейное, необходимы внутренние итерации

45. Решение нелинейного уравнения

n
Ein 1 - Ein
NEi 2 O([ zn ]2 )
zn
1
1
2
n
Ei
(
1 n
Ei Ein 1
2
)
Для нахождения значения на расстоянии “полушага” используются
итерации. На первой итерации уравнение решается явным методом
1
Ein 1
Ein zn NEin
Далее до сходимости осуществляется процесс:
n
Ei
1 m
2
(
1 n
n 1 m
Ei Ei
2
)

English Русский Правила