Трехшарнирные арки. Понятие об арке и сравнение ее с балкой

1.

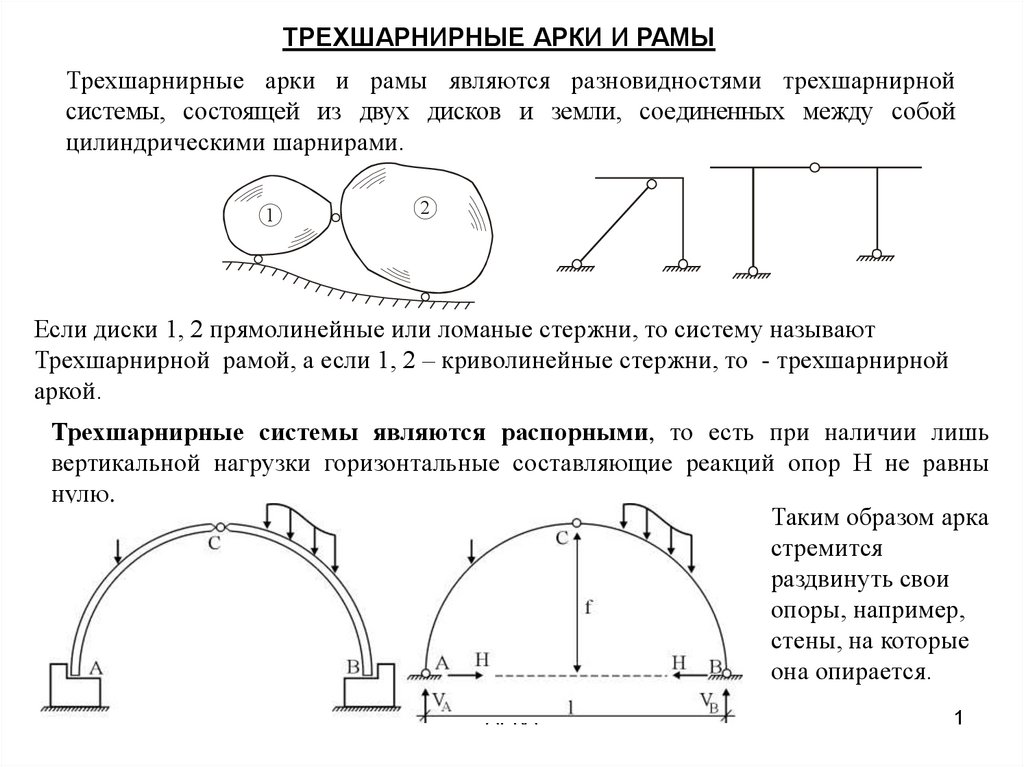
ТРЕХШАРНИРНЫЕ АРКИ И РАМЫ
Трехшарнирные арки и рамы являются разновидностями трехшарнирной
системы, состоящей из двух дисков и земли, соединенных между собой
цилиндрическими шарнирами.
1
2
Если диски 1, 2 прямолинейные или ломаные стержни, то систему называют
Трехшарнирной рамой, а если 1, 2 – криволинейные стержни, то - трехшарнирной
аркой.
Трехшарнирные системы являются распорными, то есть при наличии лишь
вертикальной нагрузки горизонтальные составляющие реакций опор Н не равны
нулю.
Таким образом арка
стремится
раздвинуть свои
опоры, например,
стены, на которые
она опирается.
АРКА
1

2.

Арочные системы многие века были одной из основных архитектурно-строительных
форм при возведении мостов, тоннелей, акведуков, перекрытий соборов, дворцов и т.п.
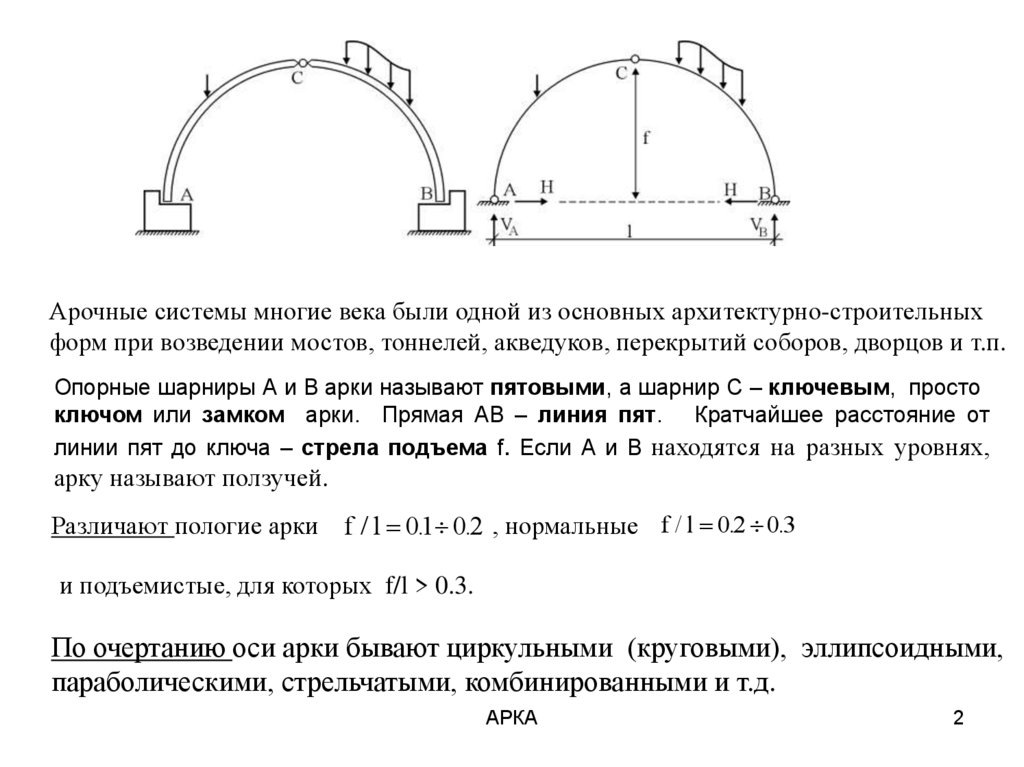
Опорные шарниры А и В арки называют пятовыми, а шарнир С – ключевым, просто
ключом или замком арки. Прямая АВ – линия пят. Кратчайшее расстояние от
линии пят до ключа – стрела подъема f. Если А и В находятся на разных уровнях,
арку называют ползучей.
Различают пологие арки f / l 01
. 0.2 , нормальные f / l 0.2 0.3
и подъемистые, для которых f/l > 0.3.
По очертанию оси арки бывают циркульными (круговыми), эллипсоидными,
параболическими, стрельчатыми, комбинированными и т.д.
АРКА
2

3.

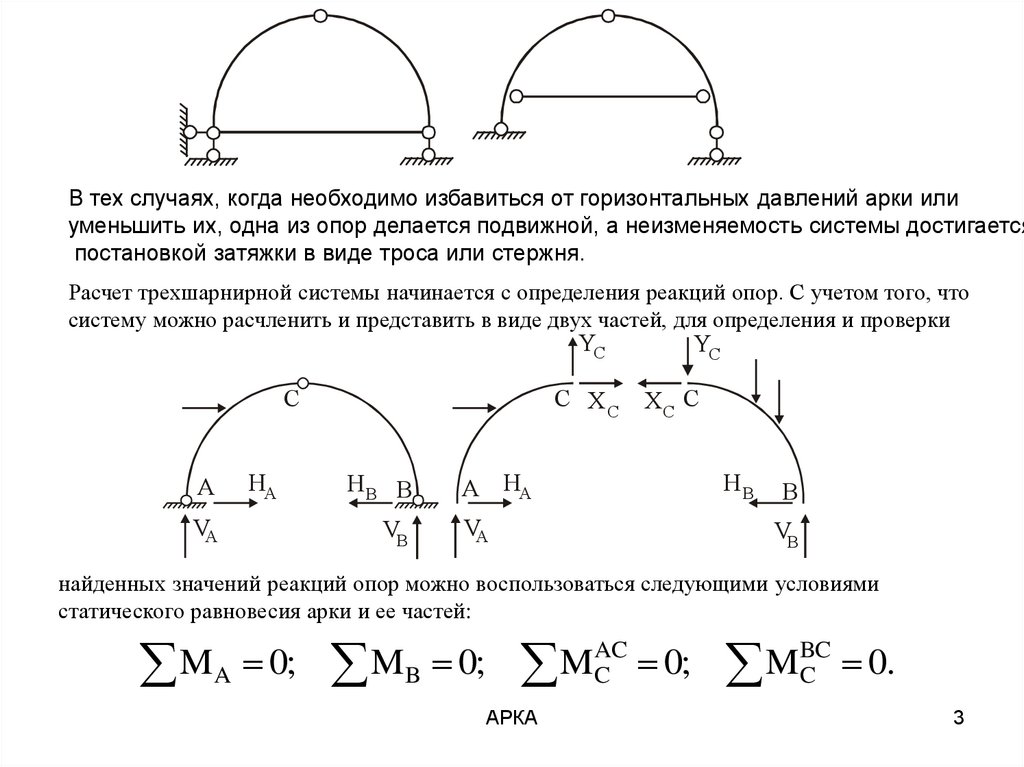
В тех случаях, когда необходимо избавиться от горизонтальных давлений арки или
уменьшить их, одна из опор делается подвижной, а неизменяемость системы достигается
постановкой затяжки в виде троса или стержня.
Расчет трехшарнирной системы начинается с определения реакций опор. С учетом того, что
систему можно расчленить и представить в виде двух частей, для определения и проверки
YC
C
A
HA
VA
YC
C X C XC C
HB B
VB
A HA
VA
HB
B
VB
найденных значений реакций опор можно воспользоваться следующими условиями
статического равновесия арки и ее частей:
MA 0;
MB 0;
AC
M
C 0;
АРКА
BC
M
C 0.
3

4.

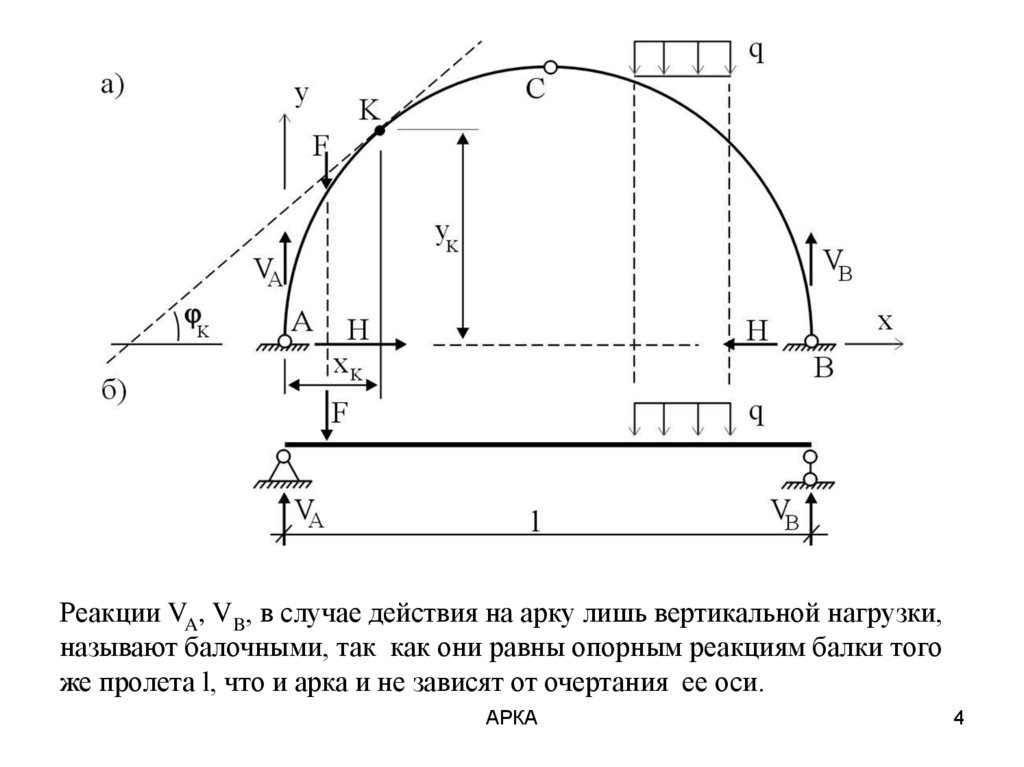
Реакции VA, VB, в случае действия на арку лишь вертикальной нагрузки,
называют балочными, так как они равны опорным реакциям балки того
же пролета l, что и арка и не зависят от очертания ее оси.
АРКА
4

5.

n
MK
QK
K
NK
K
F
t
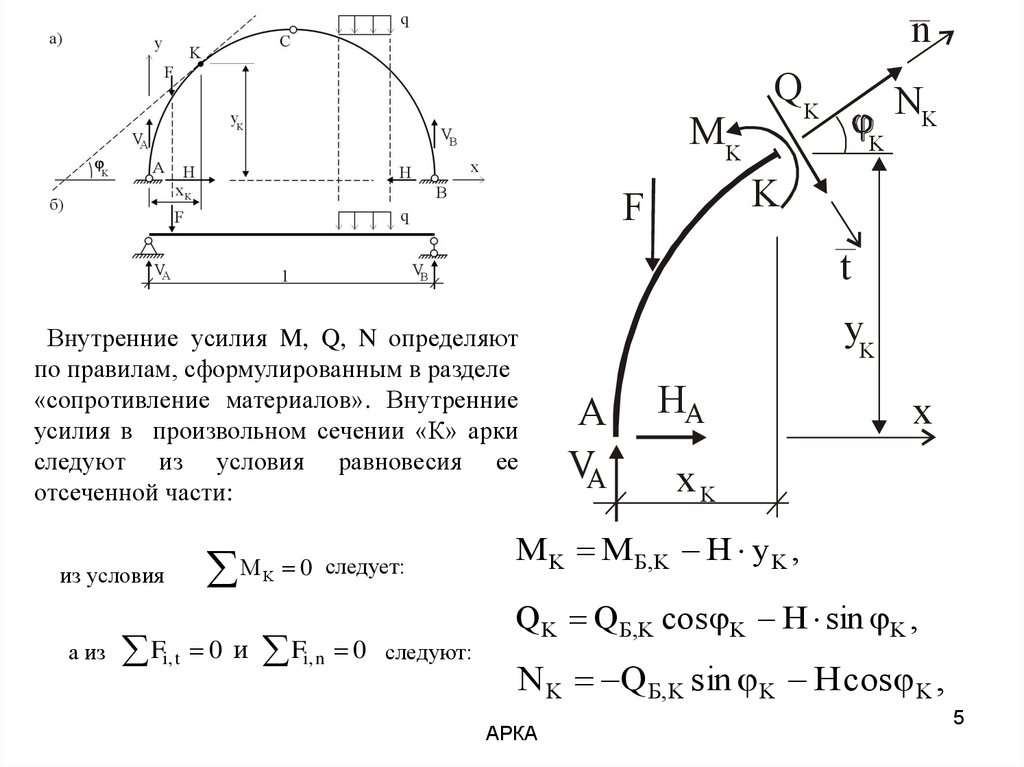
Внутренние усилия M, Q, N определяют
по правилам, сформулированным в разделе
«сопротивление материалов». Внутренние
усилия в произвольном сечении «К» арки
следуют из условия равновесия ее
отсеченной части:
из условия
а из
Fi, t 0
M K 0 следует:
и
Fi, n 0
следуют:
yK
A
VA
HA
x
xK
M K M Б,K H y K ,
Q K Q Б,K cos K H sin K ,
N K Q Б,K sin K H cos K ,
АРКА
5

6.

Трехшарнирные системы находят широкое применение в различных сооружениях: мост
перекрытия зданий и т.д. Уже из выражений для Q и M видно, что
M K M Б,K , Q K Q Б,K
то есть M и Q меньше, чем в балках. Если балка работает на изгиб, то арка – на
изгиб и сжатие. Подбором очертания оси арки, то есть подбором зависимости y =
0
f(x), можно исключить наличие в ее сечениях изгибающихNмоментов.
В случае
когда М = 0, условия работы материала арки оказываются оптимальными, что
следует из сравнения эпюр нормальных напряжений в ее поперечном сечении.
-
-
-
h
+
а) сжатие
б) изгиб
в) изгиб со сжатием
Более рациональная работа материала арки по сравнению с работой
материала балки делает первую более приемлемой при перекрытии больших
пролетов, когда балка становится экономически невыгодной. К минусам же
арки следует отнести необходимость увеличения размеров ее опорных
устройств для оказания сопротивления распору.
АРКА
6

7.

Уравнение рациональной оси арки, то есть когда М = 0, следует
при заданной вертикальной нагрузке из выражения для М:
y M Б / H.
Таким образом, при наличии лишь вертикальной нагрузки
очертание оси арки будет рациональной, если оно меняется по
закону изменения балочного момента.
АРКА
7

8.

Рассмотрим, например, арку под действием равномерно распределенной
нагрузки.
ql
x2
MБ x q
qx (l x ),
2
2
2
ql2
H M Б, C / f
,
8f
.
y MБ / H
4f
l
2
(l x ) x
или
l 2
( y f ) 2 (x )
2
l
То есть, рациональная ось арки в данном
случае – квадратная парабола с вершиной в т.
АРКА
4f
l
C ; f
2
8

9.

Рассмотрим пример построения эпюр M, Q, N в трехшарнирной арке, ось которой очерчена
по квадратной параболе. В принятой системе координат уравнение оси арки имеет вид
y x (1 x / 8).
M
M
M
Определим опорные реакции арки:
B
0 : VA 8 F 6 m q 4 2 0,
A
0 : VB 8 q 4 6 m F 2 0,
AC
C
VA 7кH,
VB 7кH,
0 : VA 4 H f F 2 m 0, H 6кH,
Проверка:
CB
M
C VB 4 H f q 4 2 7 4 6 2 2 4 2 28 28 0
АРКА
9

10.

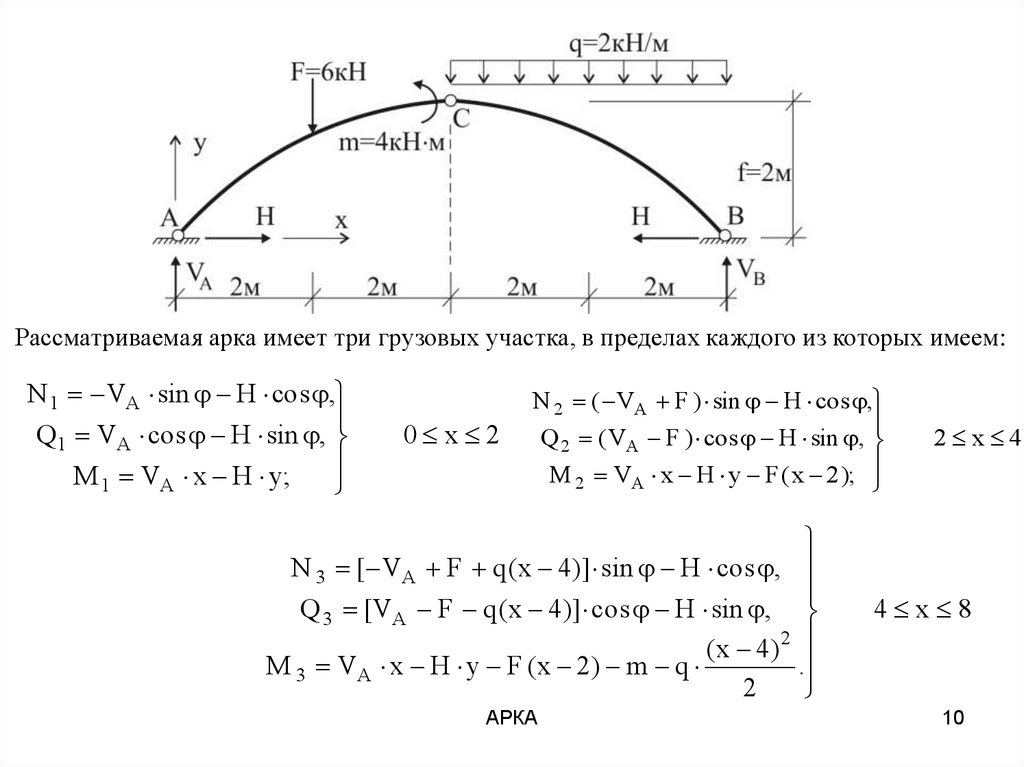
Рассматриваемая арка имеет три грузовых участка, в пределах каждого из которых имеем:
N 1 VA sin H cos ,
Q1 VA cos H sin ,
M 1 VA x H y;
0 x 2
N 2 ( VA F ) sin H cos ,
Q 2 ( VA F ) cos H sin ,
M 2 VA x H y F ( x 2 );
N 3 [ VA F q ( x 4 )] sin H cos ,
Q 3 [VA F q ( x 4 )] cos H sin ,
( x 4 )2
M 3 VA x H y F ( x 2 ) m q
.
2
АРКА
2 x 4
4 x 8
10

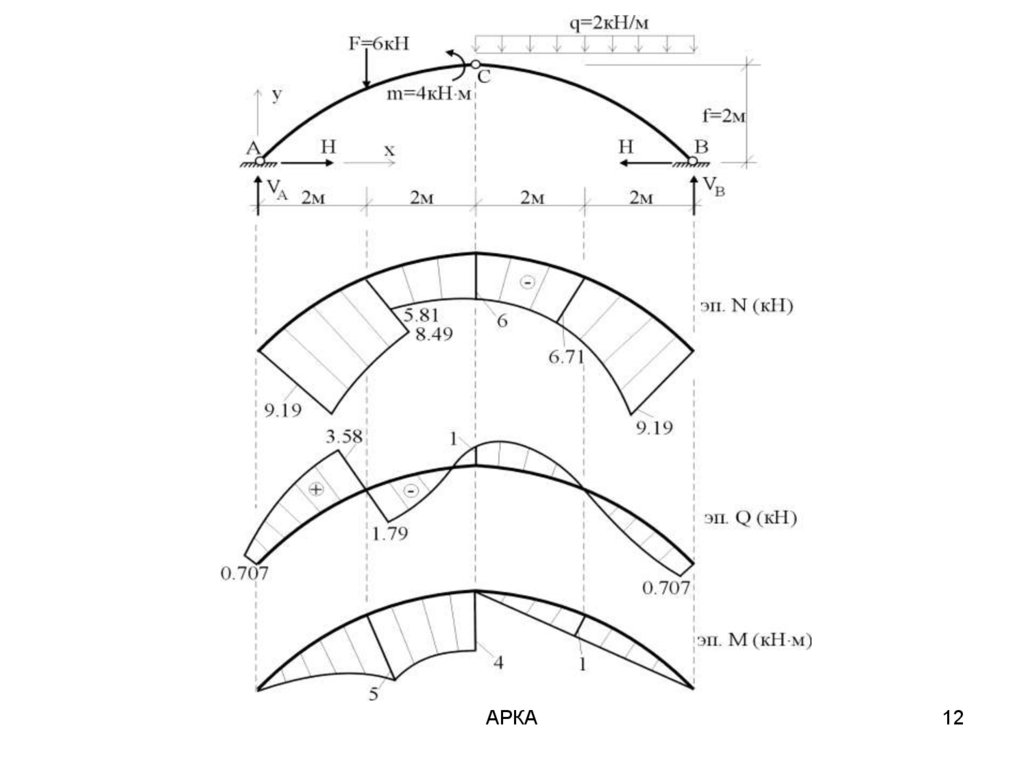
11.

Так как
tg y 1 x / 4,
Результаты вычислений
нетрудно получить и значения
y, tg , , sin , cos
sin , cos .
и N, Q и M для сечений,
отстоящих друг от друга по горизонтали на 2м, приведены в таблице.
x
(м)
y
(м)
tg
град
sin
cos
N
(кH)
Q
(кH)
M
(kHм)
0
0
1
45
0.707
0.707
-9.19
0.707
0
2
1.5
0.5
26.6
0.447
0.894
-8.49
3.58
5
-5.81
-1.79
-6
1
4
2
0
0
0
1
4
0
6
1.5
-0.5
-26.6
-0.447
0.894
-6.71
0
1
8
0
-1
-45
0.707
0.707
-9.19
-0.70
0
АРКА
11

12.

АРКА
12