Алгоритм приведения к каноническому виду уравнения с корнем. Примеры решения

1. Алгоритм приведения к каноническому виду уравнения с корнем

Примеры решения.

2.

Задача 1.
Установите, какую линию определяет уравнение
3 2
y 7
x 6 x 13, y 7, x R.
2
Нарисуйте ее график.

3.

Из условия видим, что множество значений, которые может принимать y, удовлетворяет неравенству:
y<7.
Избавимся от иррациональности. Для этого перенесем свободный член в левую сторону уравнения
y 7
3 2
x 6 x 13
2
и возведем обе части равенства в квадрат:
y 7 2 9 x 2 6 x 13 .
(1)
4
Для дальнейшего приведения к каноническому виду выделим в правой части полный квадрат:
x 2 6 x 13 x 2 2 3x 32 32 13
x 2 2 3x 32 32 13 x 3 2 4
Подставим преобразованное выражение в равенство (1)
раскроем большие скобки в правой части
y 7 2
9
x 3 2 4 ,
4
соберем все неизвестные слева
y 7
2
9
x 3
2
4
1
y 7
2
9
x 3 2 9,
4
y 7 2 9 x 3 2 9 : 9
4
- гипербола, О(3, 7), полуоси мнимая а = 2, действительная b = 3.

4.

Множество значений у: y<7.
y 7
3 2
x 6 x 13
2
y 7
9 2
x 6 x 13 .
4
2
(1)
x 2 6 x 13 x 2 2 3x 32 32 13 x 2 2 3x 32 32 13 x 3 2 4
y 7 9 x 3 2 4 ,
4
y 7 2 9 x 3 2 9 : 9
4
2
y 7 2 x 3 2
9
4
1
y 7
2
9
x 3 2 9,
4
- гипербола, О(3, 7), полуоси: мнимая а = 2, действительная b = 3.

5.

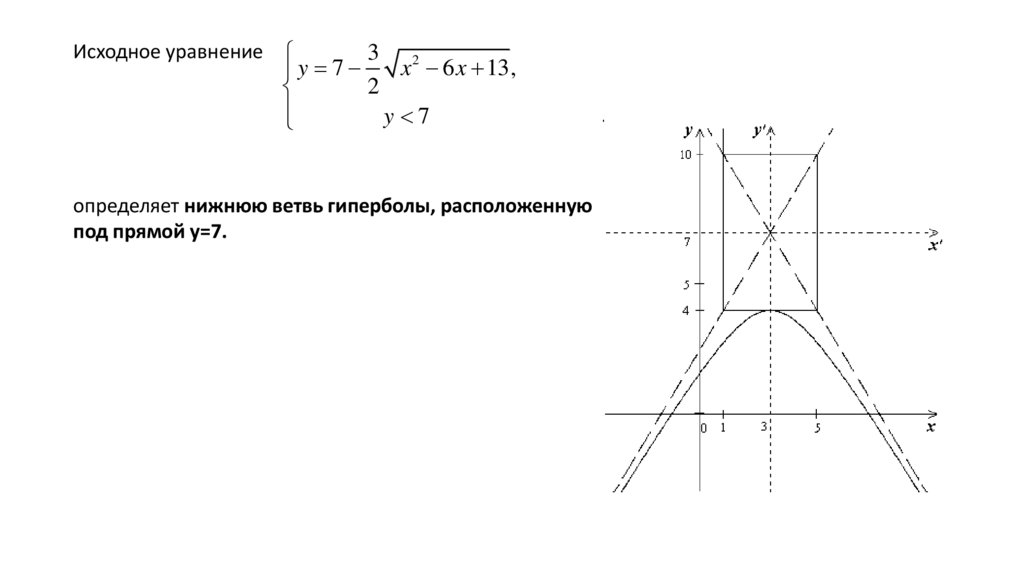
Исходное уравнение
3 2
y
7
x 6 x 13,
2
y 7
определяет нижнюю ветвь гиперболы, расположенную
под прямой y=7.

6. Задача 2.

Установите, какую линию определяет уравнение
Нарисуйте ее график.
Решение.
1 y 1
x 1
,
2
2
8 x 1 2 y 1
Учтем ОДЗ заданного уравнения:
x 1 2 1 y 1 , 8
4 2
или
y 1 8 x 1 2
y 1 0, y 1,
2
x 1
x 1 0
Вывод: исследуемое уравнение задает кривую 2-го порядка –
левая ветвь параболы с вершиной в точке (1, -1).
1
x 1
2
y 1
.
2

7. Задача 3.

Установите, какую линию определяет уравнение y 2 9 x 2 8 x .
Нарисуйте ее график.
Решение. y 2 9 x 2 8 x ,
Выделим полный квадрат:
Тогда
Искомая линия –
нижняя часть окружности:
y -2, x [-1, 9].
2
y 2 2 9 x 2 8 x
x 2 8 x x 2 2 4 x 42 42 x 2 2 4 x 42 42 x 4 2 42.
y 2 2 9 x 4 2 16
(y + 2)2 + (x – 4)2 = 52,
2
y 2 9 x 8x ,
2
или
y 2 2 x 4 2 9 16

8. КРИВЫЕ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ

РЕШЕНИЕ задач на построение

9.

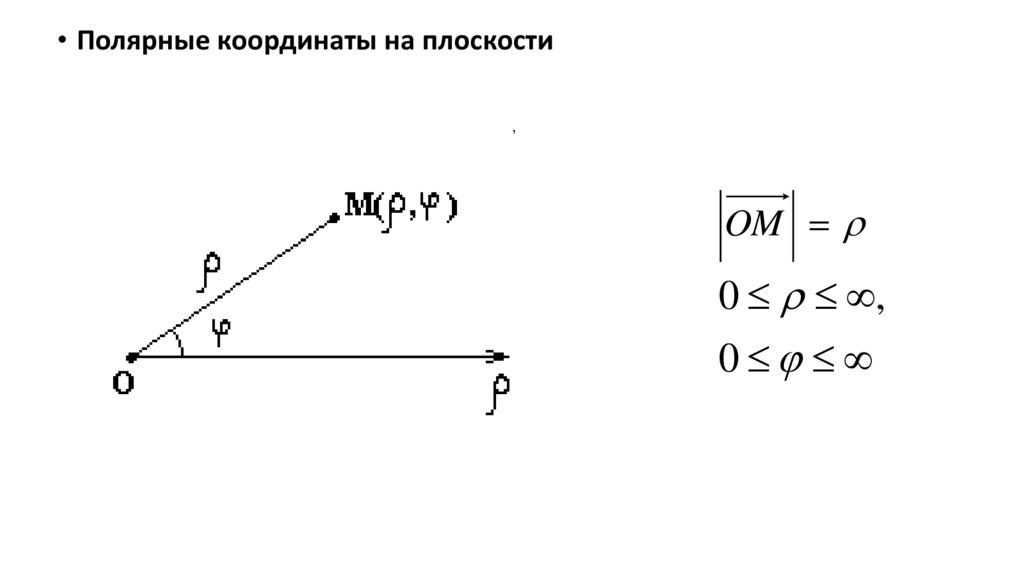
• Полярные координаты на плоскости
,
OM
0 ,
0

10.

Связь полярных координат с декартовыми
x cos ,
y sin ,
x2 y 2 ,
y
tg .
x

11.

• как построить линию в полярной системе координат?
• – Сначала необходимо отметить полюс, изобразить полярную ось и
указать масштаб. Кроме того, на первоначальном этапе желательно найти
область определения функции, чтобы сразу же исключить из
рассмотрения лишние угловые значения.
• – В большинстве случаев потребуется найти несколько точек,
принадлежащих линии. Но иногда можно обойтись только схематическим
чертежом.
• – На следующем шаге следует прочертить угловые направления и
отметить найденные значения точек.
• – Отложенные точки соединить плавной линией.
• Рассмотрим несколько типовых задачах:

12. Задача 1.

x cos ,
y sin ,
Задача 1.
x2 y 2 ,
y
tg .
x
Постройте в полярной системе координат
линию = 2a sin , a > 0.
Решение. Найдем уравнение данной линии в прямоугольной системе координат. Воспользуемся
уравнениями перехода из полярной системы координат в декартову прямоугольную (формулы
расположены в правом верхнем углу слайда). Подставим их в исходное уравнение:
x 2 y 2 2a
y
x2 y2
x2 y2
x2 + y2 – 2ay = 0,
Выделим полный квадрат для слагаемых с переменной y:
x2 + (y – a)2 = a2.
- окружность со смещенным центром.
Рисунок – в правом нижнем углу.

13. Задача 2.

• Постройте в полярной системе координат линию = 2 + cos .
Решение. 1) Найдём область определения. Поскольку полярный радиус неотрицателен, то и
правая часть уравнения линии должна подчиняться неравенству:
2 + cos 0 или cos -2, откуда - любое действительное число.
2) Найдем координаты нескольких точек и занесем их в таблицу. Например,
0
3
при =0, = 2 + cos0=2+1=3.
/2
2
Желательно составить таблицу точек с шагом для угла в /8 радиан.
1
3) Начертить «заготовку», на которой изображены радиусы при разных значениях угла
(рисунок на следующем слайде).
4) Отметить на «заготовке» найденные точки и аккуратно соединить их линией.

14.

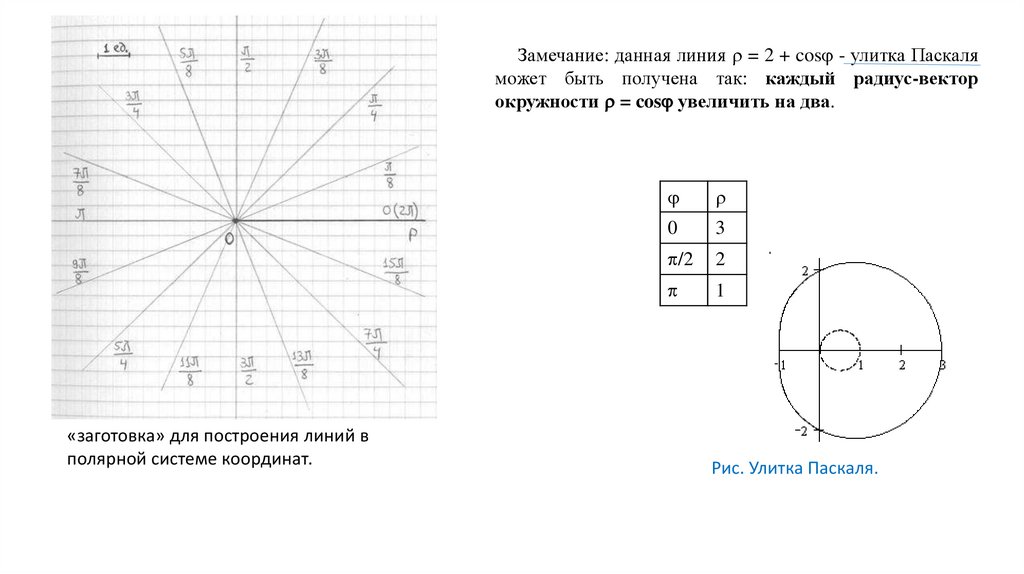
Замечание: данная линия = 2 + cos - улитка Паскаля
может быть получена так: каждый радиус-вектор
окружности = cos увеличить на два.
«заготовка» для построения линий в
полярной системе координат.
0
3
/2
2
1
Рис. Улитка Паскаля.

15. задача 3.

• Постройте в полярной системе координат линию
a sin 2 , a>0; 0 2 , 0 a
.
• Решение. 1) составим таблицу пар точек, принадлежащих данной
линии.
0
10
20
30
40
45
50
60
70
80
90
0
0,3
0,6
0,86
0,99
1
0,99
0,86
0,6
0,3
0
• 2) Для нахождения вида кривой обратимся к графику функции для
[0; 2 )

16.

= sin
/2
0
/4
3 /2 2
5 /4
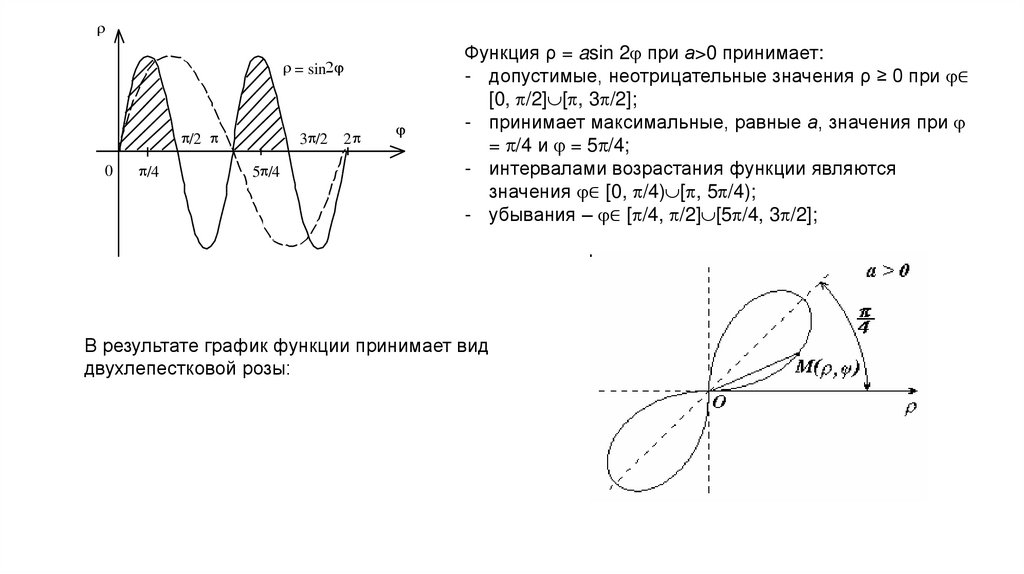
Функция ρ = asin 2 при а>0 принимает:
- допустимые, неотрицательные значения ρ ≥ 0 при ∈
[0, /2] [ , 3 /2];
- принимает максимальные, равные а, значения при
= /4 и = 5 /4;
- интервалами возрастания функции являются
значения ∈ [0, /4) [ , 5 /4);
- убывания – ∈ [ /4, /2] [5 /4, 3 /2];
В результате график функции принимает вид
двухлепестковой розы:

17. Задача 4.

• Постройте в полярной системе координат линию
9
4 5cos
Решение:
Исходя из области определения переменной , найдем пределы изменения аргумента . Очевидно,
что знаменатель дроби должен быть строго положительным:
4 – 5 cos > 0, или cos < 4/5, откуда (arccos(4/5), 2 – arccos(4/5)).
По условию (4 - 5 cos ) = 9. Воспользуемся формулами, связывающими полярные и
прямоугольные координаты.

18.

x
x2 y 2 4 5
9,
2
2
x y
4 x 2 y 2 5 x 9,
16 x 2 y 2 5 x 9 ,
2
16x2 + 16y2 = 25x2 + 90x + 81,
9x2 + 90x – 16y2 +81 = 0,
9(x + 5)2 – 16y2 = 144
( x 5)2 y 2
2 1
2
4
3
– правая ветвь гиперболы при указанных .
(Кривую можно было построить по точкам,
например, при = : = 9/1 и так далее)

19. Задача 5.

2 sin2 линию
= а2.
• Постройте в полярной системе координат
Решение: sin 2 0,
a
sin 2
0, 2 , 3 2 .
.
2
2 xy
,
Перейдем к декартовым координатам, учтем, что sin 2 2cos sin 2 2
2
x y
Отсюда, кривая принимает вид гиперболы:
(рисунок справа)
a2
y 2
x