Похожие презентации:
Продолжительность плавления термически массивных тел
1. Лекция №16
Продолжительность плавления термически массивных телПостановка задачи: в рабочем пространстве нагревается тело
правильной формы массой M0 , с характерным размером R0; в момент времени
τ = 0 температура поверхности тела стала равной tпл .
Определить время τпл , в течение которого тело полностью расплавится,
если:
нагрев симметричный и плотность теплового потока qр.м. одинакова по всей F;
плотность результирующего теплового потока qр.м. = const
физические свойства тела известны и не зависят от температуры;
в начальный момент времени температурное поле в теле параболическое;
образующийся расплав непрерывно и мгновенно удаляется с поверхности
тела;
коэффициент формы тела – ν
2.
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКАкраевой задачи теплопроводности
2t ( x , τ) 2 ν 1 t ( x , τ)
t ( x , τ)
a
2
τ
x
x
x
– уравнение Фурье.
Геометрические условия: ν = –1/2 (или 0, или +1/2);
или
0 ≤ x ≤ R;
R = R0…0;
0 ≤ x ≤ R;
R = R0…0;
Физические условия: a = const;
= const;
c = const;
= const.
Начальные условия: = 0;
t(R0,0) = tпл;
t(x,0) = tпл - ∆t0(1 – X2).
ω = 1…0.
2
3.
• Граничные условия: при нагревеt x , τ
λ
qр.м const .
x x R
ds
при x → R имеет место разрыв
градиента температуры
t x , τ
x
x
R
tпл
qs
qсм
(q р.м q s ) dτ r пл ρ ds;
ds
q р.м q s r пл ρ ,
dτ
где: ds - слой в пределах которого и происходит изменение
агрегатного состояния
qs - плотность теплового потока на выходе из слоя ds
s – толщина проплавленной части
3
4.
Постулата мгновенного регулярного режима (МРР) :dt ds
dτ
dt ω
dτ
Где: t ds – средняя температура слоя ds;
tω
– средняя температура нерасплавленной части тела.
R0 c
t ( ин) t (0) (1)
Продолжительность инерционного периода : ин
2 2 qсм
qсм R0 K T
t (0) t пл
;
Kq
(2)
qS R0 K T
t ( ин) t пл
;
Kq
(3)
4
5.
RПодставив (2) и (3) в (1) получим:
Заметим, что
qS
qсм
q
R0 c qсм R0
1
S
1
ин 2 2 q
2 4 qсм (2 2)( 2 2)a
см
qS
= (R) = (R0∙ω), где ω = R/R0;
qсм
Дифференциальные уравнения нагрева:
qсм F d рег M ds Qпл M c d t
d рег
Учитывая:
2
0 1
M ds
ds;
F
c 1
;
a
M b R2 2 ;
t пл t
qs R
;
(2 4)
F (2 2) b R
2 1
.
d рег
M ds Qпл d M c (t пл t )
F qсм
F qсм
(4)
q
2
3
S
R
d
qсм
Qпл
(5)
ds
2 1
qсм
(2 2)( 2 4) a R
5
6. Введение
Постулата мгновенного регулярного режима (МРР) : d t ds d td
d
(6)
Используя Cусл, получим: M c d q F d
S
d t F qS (2 2)qS
d
M c
R c
т.к.
qсм qS
(2 2) qS
C усл ds
R c
(7)
Средняя температура слоя ds: d t ds t пл
С учетом (8) получим:
Подставим (9) в (7) :
где:
C усл С
M
R
;
F 2 2
(2qсм qs ) ds
6
Qпл
6Qпл
C
(2qсм qS )ds
t пл t ds
(1 n) 2 8n 2 (1 n)
qS
qсм
2n
c t0
1
N
;
n N ;
(2 2)Qпл
3
(8)
(9)
(10)
t0
qсм R0
.
2
6
7.
qS( ) , найдем:
Используя полученную зависимость
qсм
(2 2) F0ин
1
8
3 N 1 ( N ) 2
3
9 3 N 1 Z (1)
;
2(2 4) N
2(2 4) N
1
(2 2) F0 рег
( N )
1
( N ) ;
2
( 2 4) N
0
Z ( )
2 3 N 2 1 4 2 ln y 2 2 ( N ) 2 (2 1) N ;
4
3
4
1
8
Z ( ) ( N ) 2 ;
3
9
1
y( ) ( Z N ) 6
3
7
8.
ωN=0,1
Из рисунка видно, что при N ≤ 0,3
зависимость ω(F0) линейная и имеет вид:
2ν 2 Foпл
0,3
2,0
1
1 ω
2ν 4 2 N
1,0
(2 2) F0
Продолжительность плавления: Foпл Foин Foрег
При N << 1 можно записать, что
пл
1 1
1
2 ν 2 2 ν 4 2 N
R02
(2 2) Qпл Qпл
R0
(2 2)a
2с t0
qсм
(11)
(12)
8
9. О
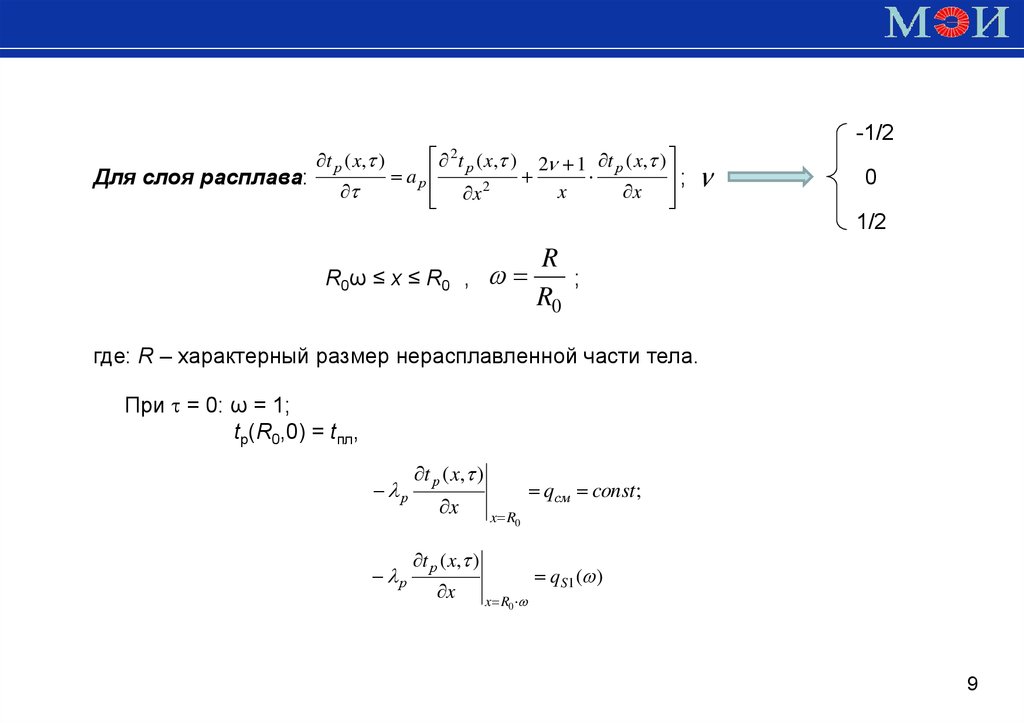
-1/2Для слоя расплава:
t р ( x, )
t р ( x, ) 2 1 t р ( x, )
aр
;
2
x
x
x
2
0
1/2
R0ω ≤ x ≤ R0 ,
R
;
R0
где: R – характерный размер нерасплавленной части тела.
При = 0: ω = 1;
tр(R0,0) = tпл,
р
р
t р ( x, )
x
qсм const ;
x R0
t р ( x, )
x
qS1 ( )
x R0
9
10. О
Для нерасплавленной части тела := -1/2, или 0, или + ½ ;
2tТ ( x, ) 2 1 tТ ( x, )
tТ ( x, )
aТ
;
2
x
x
x
0≤ x ≤ R0ω .
При = 0: ω = 1;
tТ(R0∙ω;0) =tпл;
tТ(X,0) = tпл - ∆t0(1 – X 2):
T
tT ( x, )
qS 2 ;
x
x R0
tT ( R0 , ) t пл .
Для слоя ds можно записать :
qS1 qS 2 Qпл
ds
.
d
10
11.
Эта задача может быть решена методом МРР.Асимптотическое приближение этого решения
(при N ≤ 0,3) имеет вид:
1
1 ω2 2
2 ν 2 Fo
;
2 ν 4 2 2 ν 2 N
2ν 2 Foпл
1
1
.
2ν 4 2 2ν 2 N
11
12.
СПАСИБО ЗА ВНИМАНИЕ!!!12











 Промышленность
Промышленность








