Похожие презентации:
Взаимное расположение графиков линейной функции
1. Взаимное расположение графиков линейных функций
ВЗАИМНОЕ РАСПОЛОЖЕНИЕГРАФИКОВ ЛИНЕЙНЫХ
ФУНКЦИЙ
Алгебра 7 класс
МБОУ СШ №12
Учитель: Шудраков Николай Николаевич
2. Постройте графики функции в одной системе координат
ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИИ В ОДНОЙ СИСТЕМЕКООРДИНАТ
Первый ряд
Второй ряд
Третий ряд
y=x-3
y=x-3
y=2x-1
y=2x-1
y=x+1
y - 2x=-1
3. Проверим. Первый ряд
ПРОВЕРИМ. ПЕРВЫЙ РЯДy
y=x-3
y=x-3
x
y
0
-3
2
-1
1
1
0
y=2x-1
x
y
0
-1
1
1
y=2x-1
A
x
4. Проверим. Второй ряд
ПРОВЕРИМ. ВТОРОЙ РЯДy
y=x-3
y=x-3
x
y
0
-3
2
-1
1
1
y=x+1
y=x+1
x
y
0
1
1
2
0
x
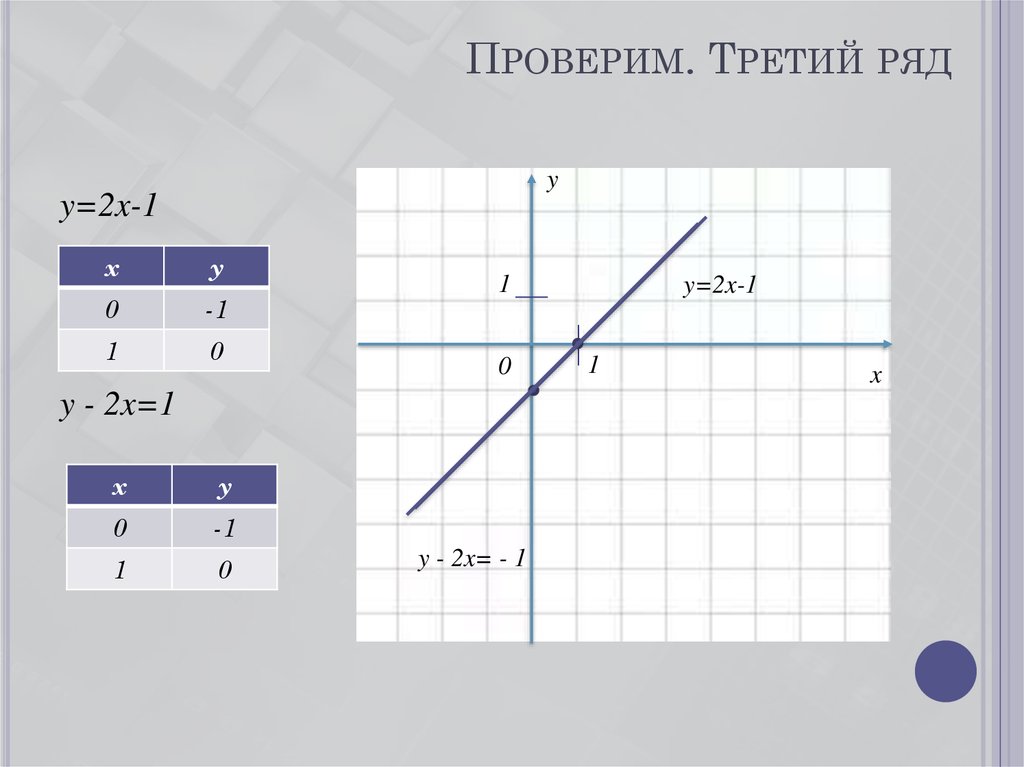
5. Проверим. Третий ряд
ПРОВЕРИМ. ТРЕТИЙ РЯДy
y=2x-1
x
y
0
-1
1
0
1
0
y - 2x=1
x
y
0
-1
1
0
y - 2x= - 1
y=2x-1
1
x
6. Рассмотрим коэффициенты графиков линейных функций
РАССМОТРИМ КОЭФФИЦИЕНТЫ ГРАФИКОВЛИНЕЙНЫХ ФУНКЦИЙ
y = k1 x + m1
y = k2 x + m2
y=x-3
y = 2x - 1
k1= 1 m1= - 3 k2= 2
m2= - 1
k1 ≠ k2
Прямые пересекаются
7. Рассмотрим коэффициенты графиков линейных функций
РАССМОТРИМ КОЭФФИЦИЕНТЫ ГРАФИКОВЛИНЕЙНЫХ ФУНКЦИЙ
y = k1 x + m1
y = k2 x + m2
y=x-3
y=x+1
k1= 1
m1= - 3 k2= 1 m2= 1
k1 = k2
m1≠ m2
Прямые параллельны
8. Рассмотрим коэффициенты графиков линейных функций
РАССМОТРИМ КОЭФФИЦИЕНТЫ ГРАФИКОВЛИНЕЙНЫХ ФУНКЦИЙ
y = k1 x + m1
y = k2 x + m2
y = 2x - 1
y - 2x=-1
y = 2x - 1
k1= 2 m1= - 1 k2= 2
k1 = k2
m1=m2
m2= - 1
Прямые совпадают
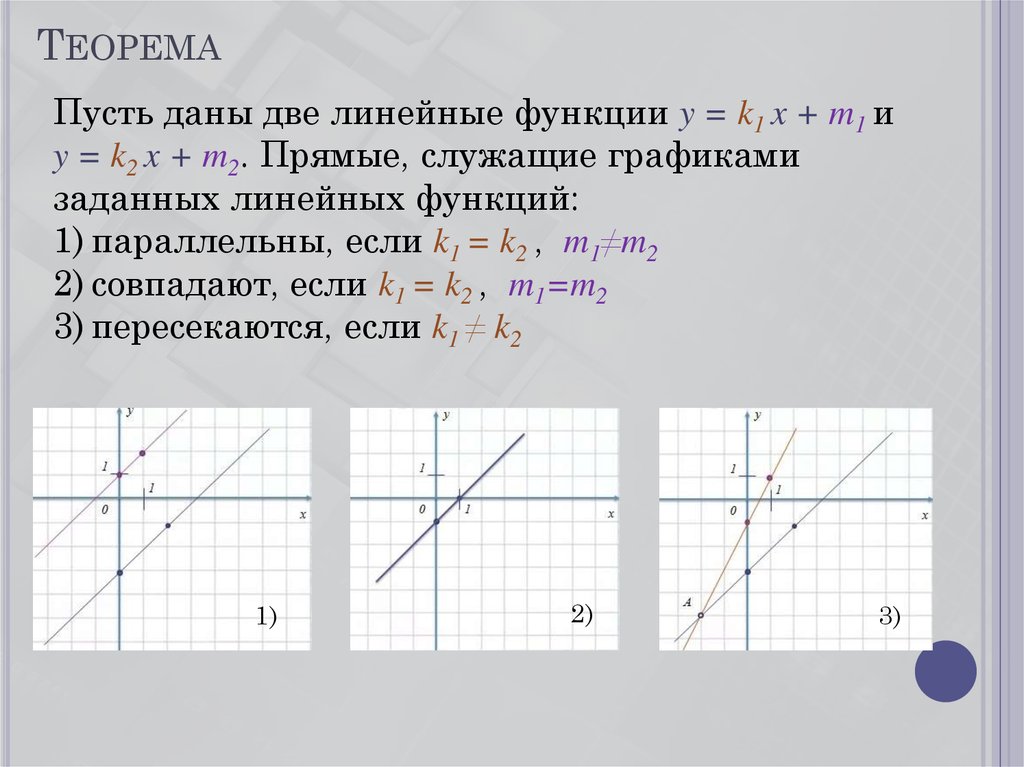
9. Теорема
ТЕОРЕМАПусть даны две линейные функции y = k1 x + m1 и
y = k2 x + m2. Прямые, служащие графиками
заданных линейных функций:
1) параллельны, если k1 = k2 , m1≠m2
2) совпадают, если k1 = k2 , m1=m2
3) пересекаются, если k1 ≠ k2
1)
2)
3)
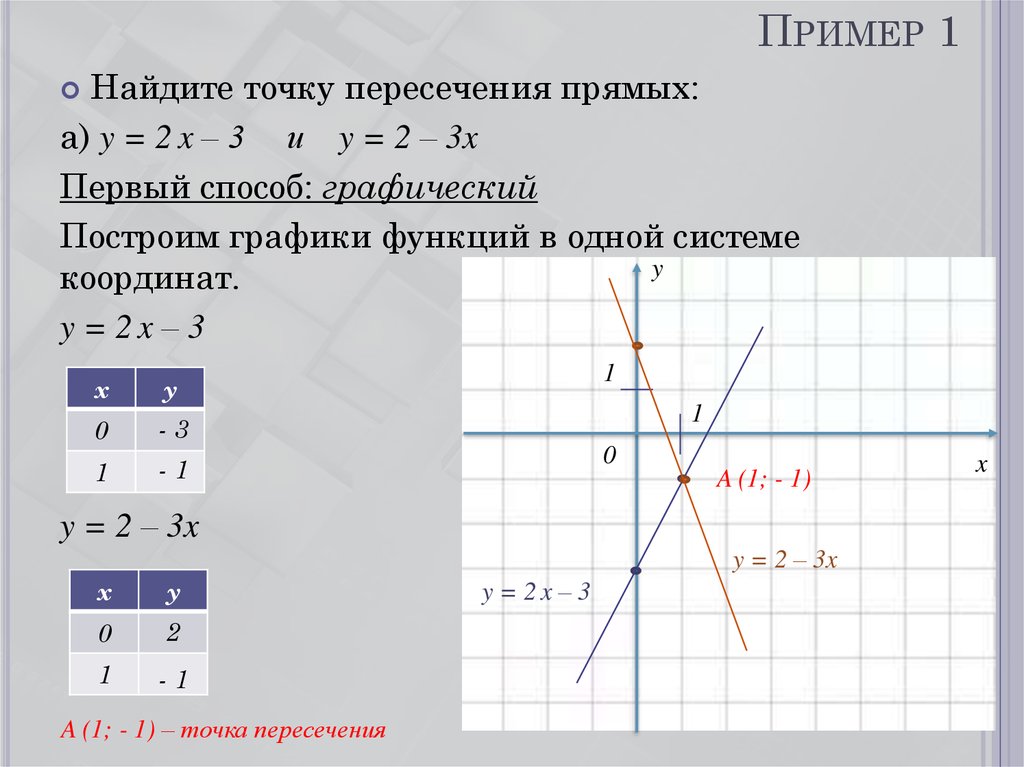
10. Пример 1
ПРИМЕР 1Найдите точку пересечения прямых:
а) y = 2 x – 3 и y = 2 – 3x
Первый способ: графический
Построим графики функций в одной системе
y
координат.
y = 2x – 3
x
y
0
-3
1
-1
1
1
0
A (1; - 1)
y = 2 – 3x
y = 2 – 3x
x
y
0
2
1
-1
A (1; - 1) – точка пересечения
y = 2x – 3
x
11. Пример 1
ПРИМЕР 1Найдите точку пересечения прямых:
а) y = 2 x – 3 и y = 2 – 3x
Второй способ: аналитический
Угловые коэффициенты прямых различны, значит прямые
пересекаются в одной точке. Это общая точка имеет
координату (x0 ; y0). Приравняв правые части и решив
уравнение, мы найдем абсциссу точки пересечения:
2 x0 – 3 = 2 – 3 x0
2 x0 + 3 x0 = 2 + 3
5 x0 = 5
x0 = 5 : 5
x0 = 1
Чтобы найти ординату, подставим полученное значение
аргумента x0 в одну из функций:
y0 = 2 x0 – 3=2·1 – 3 = - 1
A (1; - 1) – точка пересечения
12. Пример 1
ПРИМЕР 1Найдите точку пересечения прямых:
б) y = -3 x – 3 и y = -3x +2
Решение:
Так как линейные функции имеют один и тот же
угловой коэффициент (k = -3), значит прямые
y = -3 x – 3 и y = -3x +2 параллельны, то есть точки
пересечения у них нет.
13. Пример 2
ПРИМЕР 2Найдите точки пересечения прямых y = 4 x + 7 и
y = - 2x + 7.
Решение:
Так как угловые коэффициенты у функций
различны (k1 ≠ k2 , k1 = 4, k2 = - 2), значит прямые
пересекаются в одной точке.
Коэффициент m соответствует ординате точки
пересечения графика с осью Oy. Так как
коэффициенты m1=m2 равны, значит точка
пересечения графиков линейных функций имеет
координату (0 ; 7).
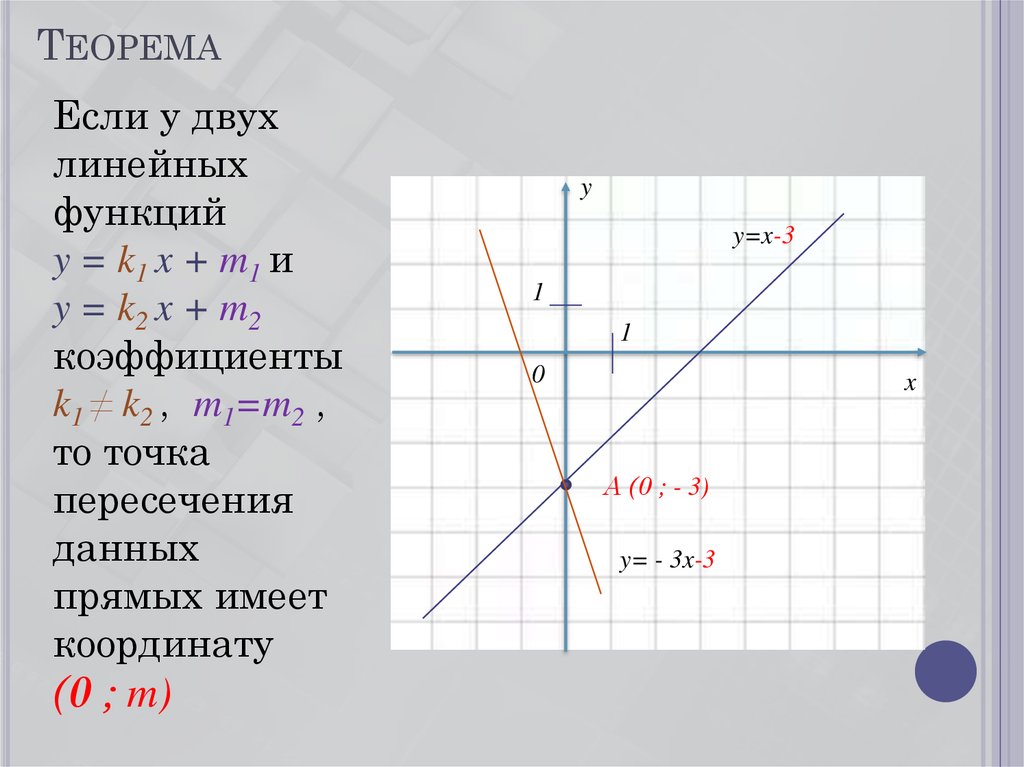
14. Теорема
ТЕОРЕМАЕсли у двух
линейных
функций
y = k1 x + m1 и
y = k2 x + m2
коэффициенты
k1 ≠ k2 , m1=m2 ,
то точка
пересечения
данных
прямых имеет
координату
(0 ; m)
y
y=x-3
1
1
0
x
А (0 ; - 3)
y= - 3x-3
15. В классе
В КЛАССЕРТ №10.3
РТ №10.4
№ 10.1 (вг)
№ 10.2 (вг)
№ 10.3 (вг)
№ 10.10 (вг)
№ 10.11 (вг)
№ 10.12 (вг)
№ 10.13 (вг)
№ 10.16 (вг)
16. Подведем итоги
ПОДВЕДЕМ ИТОГИЗаданы прямые:
y = k1 x + m1
y = k2 x + m 2
Какие варианты расположения графиков
данных функций возможны?
От чего зависит взаимное расположение
данных прямых?
Что вы можете сказать о взаимном
расположении на координатной плоскости
графиков линейных функций: y=2x+3 и y=3x-2;
y=2x+3 и y=2x ?
17. Домашнее задание
ДОМАШНЕЕ ЗАДАНИЕ§10, с.60 – 62, ответить на вопросы
№ 10.1 (аб)
№ 10.2 (аб)
№ 10.3 (аб)
№ 10.10 (аб)
№ 10.11 (аб)
№ 10.12 (аб)
№ 10.13 (аб)
Просмотреть видео-урок:
http://interneturok.ru/algebra/7-klass/glava2-lineynaya-funktsiya/vzaimnoeraspolozhenie-grafikov-lineynyh-funktsiy













 Математика
Математика








