Похожие презентации:
«Греческое» хеджирование. МОФР тема 4
1. 4. «Греческое» хеджирование
1. Дельта-хеджирование.2. Гамма-хеджирование.
3. Коэффициенты тета, ро и вега.
2.
1. Дельта-хеджированиеЕсли финансовый институт продает на
внебиржевом рынке тот или иной опцион, то
он подвергается рыночному риску, так как за
опцион он получает фиксированную сумму
− премию за опцион, а его доход (убыток)
зависит от спот-цены базисных активов на
момент исполнения опциона.
Например, в случае продажи европейского
опциона «колл» прибыль финансового
института на момент исполнения этого
опциона оценивается следующим образом:
r ( T t )
c
e
, если ST K ;
r ( T t )
ce
max{ST K ;0}
r ( T t )
K
S
c
e
, если ST K .
T
2
3.
Продавая опцион, финансовый институт можетпонести очень большие убытки и поэтому
заинтересован в снижении этого рыночного
риска.
Коэффициентом дельта (delta) финансового
инструмента, производного от данных
базисных активов, называется частная
производная стоимости этого инструмента
по спот-цене базисных активов, т. е.
П
.
S
3
4.
Основное свойство коэффициента дельтаЕсли спот-цена базисных активов мгновенно
изменяется на величину S , а все остальные
факторы, влияющие на стоимость
производного финансового инструмента,
останутся неизменными, то приращение
стоимости этого инструмента П можно
приближенно оценить следующим образом:
П ( S ).
4
5.
Имеют место следующие утверждения:1) Коэффициент дельта базисных активов
всегда равен 1.
2) Коэффициент дельта фьючерсного
контракта на активы с постоянной
дивидендной доходностью можно найти по
формуле:
F e
( r q )(T t )
где q — постоянная дивидендная доходность
при непрерывном начислении;
r — безрисковая процентная ставка при
непрерывном начислении;
Т — дата поставки активов.
5
6.
3) Коэффициенты дельта европейскихопционов на активы с постоянной
дивидендной доходностью q определяются
равенствами:
c e q (T t )Ф(d1 );
p e q (T t )Ф( d1 );
S
ln (T t )(r q )
K
2
d
.
где 1
T t
2
6
7.
Пример. Рассмотрим 5-месячный европейскийопцион «пут» на бездивидендную акцию с ценой
исполнения 100 долл., когда текущая спот-цена
акции равна 100 долл., волатильность акции
оценивается в 40%, а безрисковая процентная
ставка при непрерывном начислении равна 8%.
S = 100 долл.; K = 100 долл.; г = 0,08; q = 0; Т - t
= 5/12; = 0,4;
2
100 5
0,4
5
d1 ln
(0,08
) / 0,4
0,26
100 12
2
12
Ф (−0,26) = 0,3974. Следовательно,
p =-0,3974, т.е.
7
8.
если цена базисной акции мгновенно вырастетна 1 долл., то цена опциона «пут» на эту
акцию уменьшится на 0,397 долл.
4) Коэффициенты дельта американских
опционов можно найти приближенно на
основе n-этапной биномиальной модели:
c
c(1) c(0)
S (e
hn
e
hn
)
; p
p(1) p(0)
S (e
hn
e
hn
;
)
T t c(1), p(1) - стоимость в t + hn;
hn
;
c(0), p(0) - стоимость в t + 0hn.
n
8
9.
5) Коэффициент дельта портфеля финансовыхинструментов, производных от одних и тех
же базисных активов, является линейной
комбинацией коэффициентов дельта этих
финансовых инструментов.
9
10.
Пример. Рассмотрим портфель, состоящий изпокупки ₤ 10 000, из короткой позиции по
9-месячному фьючерному контракту на
₤5000 и из длинной позиции по 6месячному европейскому опциону «пут» на
₤2000 с ценой исполнения $1,60. Найдем
коэффициент дельта портфеля, когда
текущий обменный курс— $1,62, за один
фунт, волатильность обменного курса
оценивается в 15%, а безрисковые
процентные ставки при непрерывном
начислении в США и Англии равны 10 и 13%
соответственно.
10
11.
Найдем коэффициент дельта фьючерсногоконтракта на один фунт стерлингов.
9
Так как r 0,10; rf 0,13; T t
, то
12
*
F e
( r r f )(T t )
*
e
9
(0,10 0,13)
12
0,9778
Вычислим коэффициент дельта опциона «пут»
на один фунт стерлингов. Так как
S = 1,62 долл.; K = 1,60 ДОЛЛ.; = 0,15; г =
0,10; Т−t=6/12, то
1,62 6
0,152
S
2
(0,10 0,13
)
ln (T t )(r rf ) ln
2
2 1,60 12
d1 K
0,03
T t
6
0,15
12
11
12.
ТогдаФ( d1 ) Ф( 0,03) 0,4880.
p e
r f (T t )
Ф( d1 ) e
6
0,13
12
0, 4880 0, 4573
Следовательно, коэффициент дельта
рассматриваемого портфеля можно найти
следующим образом:
Δ = 10 000 • 1 - 5000 • 0,9778 + 2000
(-0,4573) = 4196,4.
Это означает, что при падении обменного
курса на $0,01, стоимость всего портфеля
снизится на $41,96.
12
13.
Портфель финансовых инструментов,производных от одних и тех же базисных
активов, называют дельта-нейтральным
(delta-neutral), если коэффициент дельта
этого портфеля равен 0.
Если инвестор занимает некоторую позицию
по производному финансовому инструменту,
то, занимая соответствующую позицию по
какому-то другому финансовому
инструменту на те же базисные активы, он
может образовывать дельта-нейтральный
портфель, т. е. дельта-нейтрализовать свою
первоначальную позицию.
13
14.
Пример . Финансовый институт продал 6месячный европейский опцион «пут» на₤2000 с ценой исполнения $1,60, когда
текущий обменный курс — $1,62, за один
фунт, волатильность обменного курса
оценивается в 15%, а безрисковые
процентные ставки при непрерывном
начислении в США и в Англии равны 10 и
13% соответственно.
Определить, сколько фунтов стерлингов
следует купить (или продать), чтобы дельтанейтрализовать базисную позицию.
14
15.
Коэффициент дельта европейского опциона«пут» равен -0,4573.
Обозначим через х количество фунтов
стерлингов, покупаемых для дельтанейтрализации. Тогда
х − 2000 • (-0,4573) = 0.
Откуда найдем, что х = -914,6.
Таким образом, для дельта-нейтрализации
базисной позиции требуется произвести
продажу 914,6 фунтов стерлингов.
15
16.
Дельта-хеджирование риска, связанного сизменением цены базисных активов на рынке,
сводится к следующему:
выбирается некоторый биржевой инструмент,
производный от тех же базисных активов;
покупая или продавая выбранный инструмент,
базисная позиция дельта-нейтрализуется;
инвестиционный портфель периодически
ребалансируется, т. е. при помощи операций с
выбранным инструментом восстанавливается
дельта-нейтральность этого портфеля,
утрачиваемая из-за изменения цены базисных
активов и течения времени.
16
17.
Пример. Финансовый институт продал 5недельный европейский опцион «колл» на100 000 бездивидендных акций с ценой
исполнения $50, когда текущая цена акции
равна $49, волатильность акции составляет
20%, а безрисковая процентная ставка равна
5%.
Для хеджирования своей позиции финансовый
институт решает использовать операции с
базисной акцией и ребалансировать свою
позицию еженедельно.
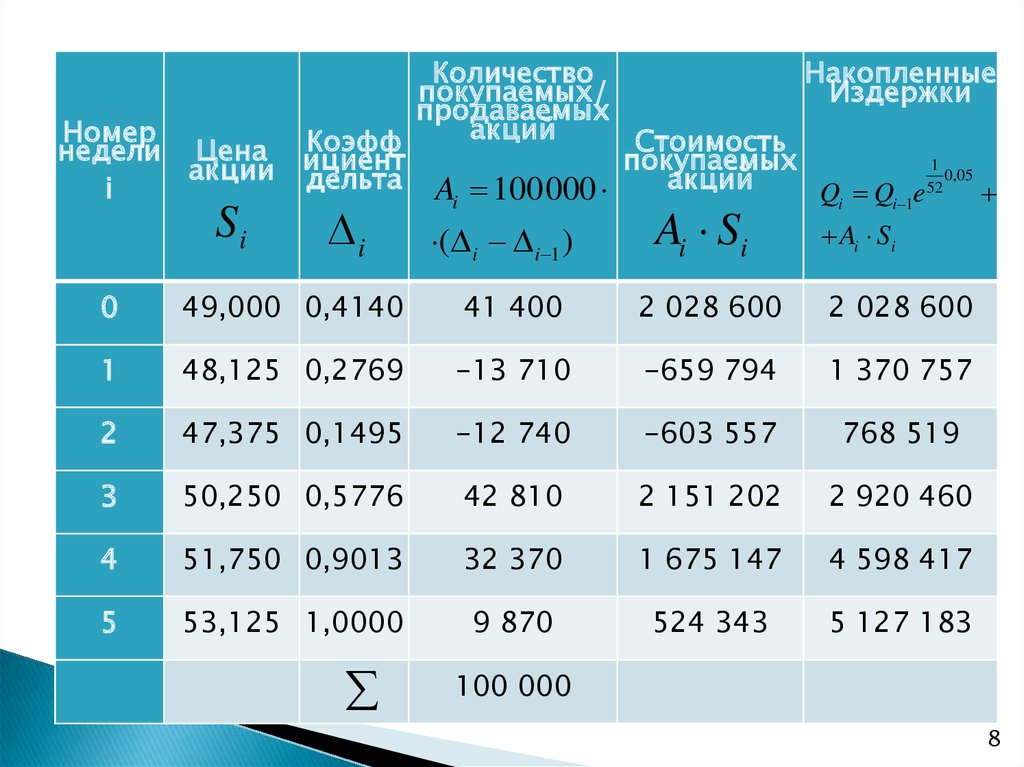
В таблице приведен сценарий изменения цены
базисной акции и расчет издержек
финансового института на дельтахеджирование.
17
18.
КоличествоНакопленные
покупаемых/
Издержки
продаваемых
акций
Номер
Коэфф
Стоимость
недели Цена ициент
покупаемых
1
акции дельта
0,05
акций
52
i
Ai 100000
Qi Qi 1e
Si
i
( i i 1 )
Ai Si
Ai Si
0
49,000 0,4140
41 400
2 028 600
2 028 600
1
48,125 0,2769
-13 710
-659 794
1 370 757
2
47,375 0,1495
-12 740
-603 557
768 519
3
50,250 0,5776
42 810
2 151 202
2 920 460
4
51,750 0,9013
32 370
1 675 147
4 598 417
5
53,125 1,0000
9 870
524 343
5 127 183
100 000
1
8
19.
В момент исполнения опциона финансовыйинститут обязан продать 100 000 акций по
цене исполнения опциона в $50.
Следовательно, чистые затраты финансового
института составят $5 127 183− $5 000 000
= $127 183, а приведенные чистые затраты
равны
5
$127183 e
0,05
52
$126573
Премия за опцион составляет $87 889. Таким
образом, чистые приведенные издержки
финансового института (без учета
комиссионных) равны
$126 573 − $87 889 = $38 684.
19
20.
При отсутствии хеджирования чистыеприведенные издержки составили бы
5 312 500USD e
0,05
5
52
87 889USD 5 199 131 USD
20
21.
2. Гамма-хеджированиеКоэффициентом гамма (gamma) финансового
инструмента, производного от данных
базисных активов, называется частная
производная второго порядка от стоимости
этого инструмента по цене базисных
2
активов, т. е.
S
2
Коэффициент гамма производного
финансового инструмента можно определить
как частную производную от коэффициента
дельта этого инструмента по цене базисных
активов, т. е.
S
21
22.
Основное свойство коэффициента гаммаЕсли спот-цена базисных активов мгновенно
изменится на величину δS, а все остальные
факторы, влияющие на стоимость
производного финансового инструмента,
останутся без изменения, то приращение
стоимости этого инструмента ΔП можно
приближенно оценить следующим образом:
S ( S ) 2
2
22
23.
Имеют место следующие утверждения:Коэффициенты гамма базисных активов и
фьючерсных контрактов на эти активы
всегда равны 0.
Коэффициенты гамма европейских
опционов на активы с постоянной
дивидендной доходностью q определяются
равенством:
d12
c p
d1
1
1
e
q (T t )
e
2 S T t
S
2
ln (T t ) r q
X
2
T t
2
;
.
23
24.
Коэффициенты гамма американскихопционов можно найти приближенно на
основе n-этапной биномиальной модели:
c(2) c(1) c(1) c(0)
2
c 2 2
;
2
2
2
S (un d n ) un 1
dn 1
p(2) p(1) p(1) p(0)
2
p 2 2
;
2
2
2
S (un d n ) un 1
dn 1
un e
hn
, dn e
hn
T t
, hn
n
c(0), p(0) - стоимость в t +0 hn
24
25.
Коэффициент гамма портфеля финансовыхинструментов, производных от одних и тех
же базисных активов, является линейной
комбинацией коэффициентов гамма этих
инструментов.
Портфель финансовых инструментов,
производных от одних и тех же базисных
активов, называется гамма-нейтральным
(gamma-neutral), если коэффициенты дельта
и гамма этого портфеля равны нулю.
25
26.
Если инвестор занимает некоторую позициюпо производному финансовому инструменту,
то, занимая соответствующие позиции по
двум другим финансовым инструментам,
производным от тех же самых базисных
активов, он может образовать гамманейтральный портфель.
Пример. Инвестор приобрел финансовый
инструмент, производный от некоторых
базисных активов, коэффициенты дельта и
гамма которого равны 0,50 и 0,02
соответственно.
26
27.
Как гамма-нейтрализовать данную позицию,используя сами эти активы и биржевые опционы
на них, если коэффициенты дельта и гамма
биржевого опциона 1,5 и 0,01?
Предположим, что для гамма-нейтрализации
позиций инвестора необходимо купить х единиц
базисных активов и у биржевых опционов на эти
активы. Тогда должны выполняться следующие
равенства:
0,50 x 1 y 1,5 0,
0,02 y 0,01 0.
у = −2, х= 2,5. Необходимо купить 2,5 единиц
базисных активов и произвести продажу двух
биржевых опционов на эти активы.
27
28.
Гамма-хеджирование предполагаетследующие действия:
выбираются два биржевых инструмента,
производных от тех же активов, что и
базисный инструмент;
покупая или продавая выбранные
финансовые инструменты, базисная позиция
гамма-нейтрализуется;
инвестиционный портфель периодически
ребалансируется, т. е. на основе операций с
выбранными инструментами
восстанавливается его гамманейтральность.
28
29.
3. Коэффициенты тета, ро и вегаКоэффициентом тета производного
финансового инструмента называют частную
производную стоимости этого инструмента
по времени, т. е.
.
t
Коэффициент тета оценивает скорость
изменения стоимости производного
инструмента при условии, что все остальные
факторы, влияющие на его стоимость,
остаются неизменными.
29
30.
Для финансовых инструментов, производныхот активов с постоянной дивидендной
доходностью, цена которых определяется
геометрическим броуновским движением,
имеет место следующее равенство:
2 2 2
(r q) S
S r .
2
В частности, если портфель финансовых
инструментов, производных от одних и тех
же активов, является гамма-нейтральным, то
равенство принимает вид:
r .
30
31.
Рассмотрим 6-месячный европейский опцион«пут» на 2000 фунтов стерлингов с ценой
1,60 долл., когда текущий обменный курс −
1,62 долл, за один фунт, волатильность
обменного курса оценивается в 15%, а
безрисковые процентные ставки при
непрерывном начислении в США и в Англии
равны 10 и 13% соответственно.
Коэффициент дельта опциона равен 2000
(-0,4573) = -914,6 а его коэффициент гамма
можно найти следующим образом:
2 000
1
2 S T t
e
q (T t )
e
d12
2
31
32.
2 0001
2 1,62 0,15 0,5
e 0,13 0,5 e
0,032
2
4349,35
Стоимость данного опциона можно найти по
формуле
p Ke
r (T t )
( d 2 ) Se
q (T t )
( d1 )
где q rf
d1 0,03; d 2 d1 T t ) 0,03 0,15 0,5 0,076
p 2 000{1,60e 0,10 0,5 ( ( 0,076)) 1,62e 0,13 0,5 ( 0,03)} 4349,35;
Тогда
0,10 147,17 (0,10 0,13) 1,62 ( 914,6)
0,152
1,622 4349,35 158,14.
2
32
33.
Таким образом, за 10 дней стоимость опционаснизится на
10
$158,14
$4,33
365
только за счет фактора времени.
33
34.
Коэффициентом ро (ρ) финансовогоинструмента называется частная производная
стоимости этого инструмента по безрисковой
процентной ставке, т. е.
r
В случае фьючерсного контракта на активы с
постоянной дивидендной доходностью q
коэффициент находится по формуле:
S (T t )e( r q )(T t )
34
35.
Для европейских опционов на активы спостоянной дивидендной доходностью
r (T t )
c K (T t )e
(d 2 ),
r (T t )
p K (T t )e
( d 2 ).
Коэффициент po используется при
хеджировании процентного риска, т. е.
риска, связанного с изменениями
безрисковой процентной ставки, точно так
же, как коэффициент дельта используется
для хеджирования рыночного риска.
35
36.
Кроме того, если на биржевом рынке имеетсянесколько различных финансовых
инструментов, производных от одних и тех
же активов, то с помощью коэффициентов ро
и дельта можно построить хеджирование
одновременно и рыночного, и процентного
рисков. Для этого достаточно сформировать
портфель с нулевыми коэффициентами ро и
дельта и периодически его
ребалансировать.
36
37.
Коэффициентом вега производногофинансового инструмента называется
частная производная стоимости этого
инструмента по волатильности базисных
активов, т. е.
Для европейских опционов на активы с
постоянной дивидендной доходностью
справедливо равенство:
c p S T t
1
2
e
d12
2
e
q (T t )
.
37
38.
Коэффициент вега используется дляхеджирования риска, обусловленного
возможными изменениями волатильности
базисных активов.
Если на биржевом рынке имеется достаточно
много различных финансовых инструментов,
производных от одних и тех же активов, то,
используя коэффициенты дельта, гамма, ро, вега
и др., можно осуществить хеджирование разных
рисков одновременно.
Такое хеджирование потребует большого числа
различных операций с биржевыми
инструментами, что значительно увеличит
транзакционные расходы, которые могут
сделать такое хеджирование заведомо
убыточным.
38





































 Финансы
Финансы








