Похожие презентации:
Простейшие тригонометрические уравнения
1.
Практическая работа на тему:Простейшие тригонометрические
уравнения
Выполнили:
Студенты группы «З-11»
Калашникова Анастасия
Кукин Никита
2016
2. Простейшие тригонометрические уравнения
Решениетригонометрических
уравнение
Простейшие тригонометрические
уравнения
3. X=〖(-1)〗^n arcsina+πn, n∈Z a∈[-1;1] x∈[-π/2;π/2] arcsin(-a)=-arcsina
Уравнение4. Частные виды решения уравнений sinx=a
Частные виды решения уравнений5. Уравнение Cosx=a
Уравнение6. Частные виды решения уравнений Cosx=a
Частные виды решения уравнений7. Уравнение tgx=a
Уравнение8. Частные виды решения уравнений
=9. Уравнение c
=∈
∈[− ;]
c (− )=− c
10. Частные виды решения уравнений c
=c =0
= , ∈
c =−1
c
+ , ∈
c =1
c
=+
+∈
,
11. Уравнения, сводящиеся к квадратным
2.Пусть Sin x = y ,тогда получим уравнение . Его корни y=1 и y=-
Решение исходного уравнения сводится к решению
простейших уравнений Sin x=1 и Sin x=-2
12. Уравнение вида aSinx+bCosx=0
Поделив уравнение на , получим 2tgx-3=0Решение исходного уравнения сводится к
решению простейшего уравнения
13. Уравнение вида aSinx+bCosx=0
1.. Получаем:
2 + =0
14.
Поделив это уравнение на Обозначаем , получаемуравнение
Его корни и y=
Решение сводится к простейшим уравнениям tg x=1 и tg x=
15. Уравнения, решаемые разложением левой части на множители
Решение сводится к простейшим тригонометрическимуравнениям


![X=〖(-1)〗^n arcsina+πn, n∈Z a∈[-1;1] x∈[-π/2;π/2] arcsin(-a)=-arcsina X=〖(-1)〗^n arcsina+πn, n∈Z a∈[-1;1] x∈[-π/2;π/2] arcsin(-a)=-arcsina](https://cf.ppt-online.org/files/slide/t/tslh9zLHR8aDxiJfWUneMCYK10g3uq45SkmF7y/slide-2.jpg)
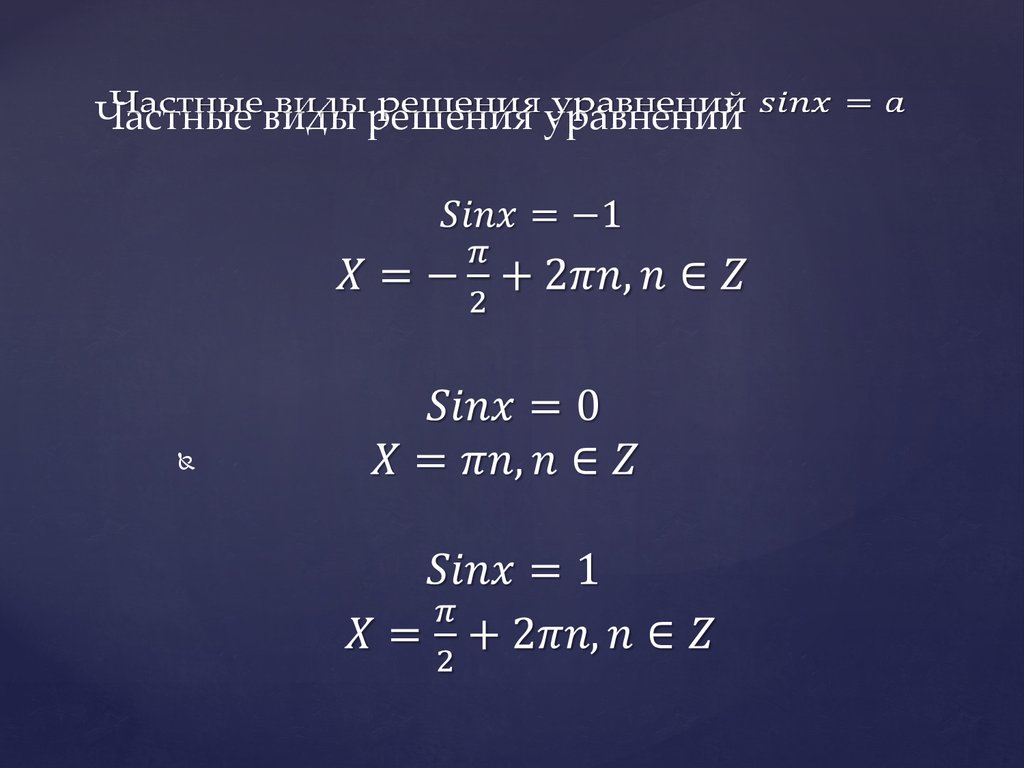
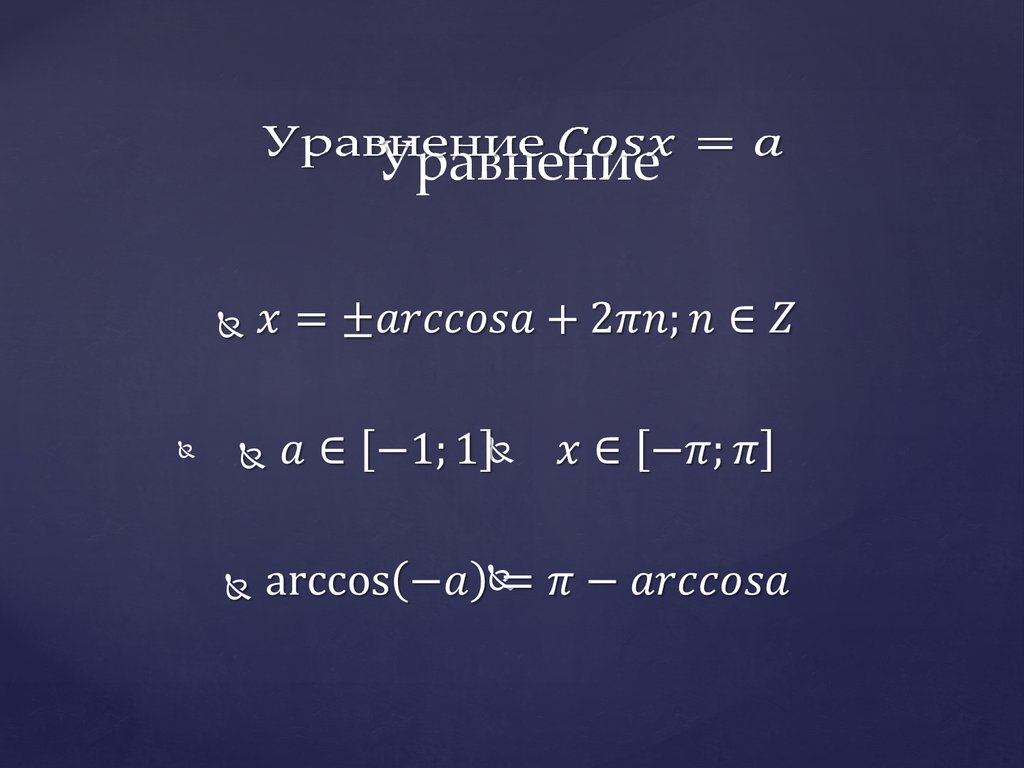
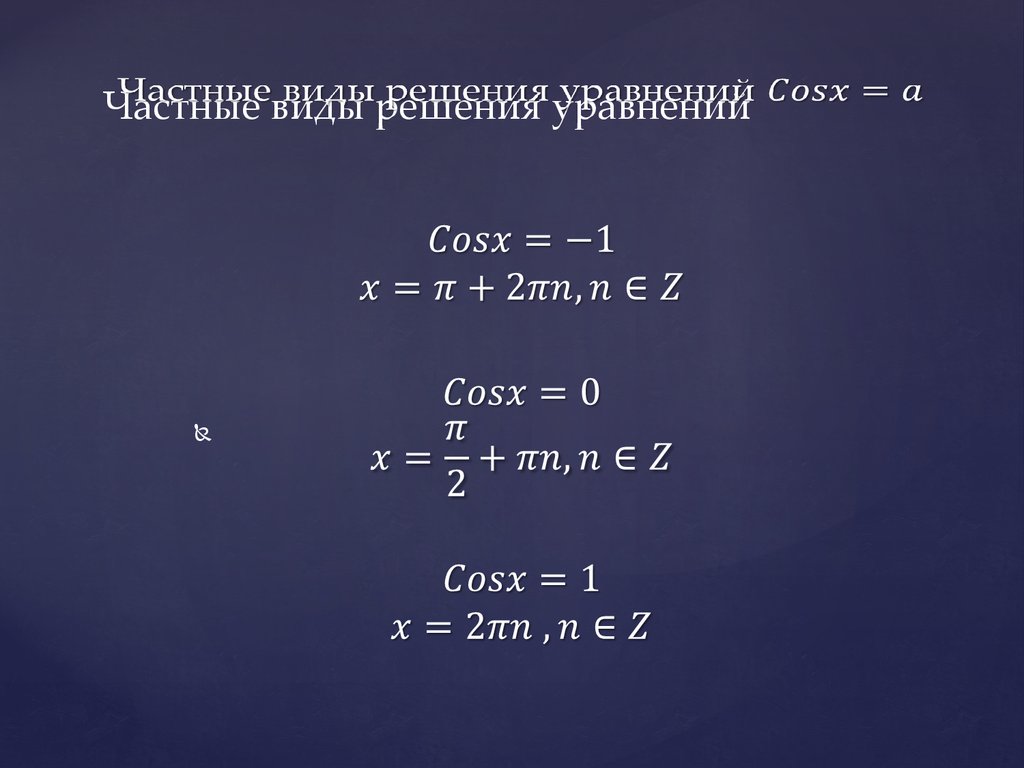
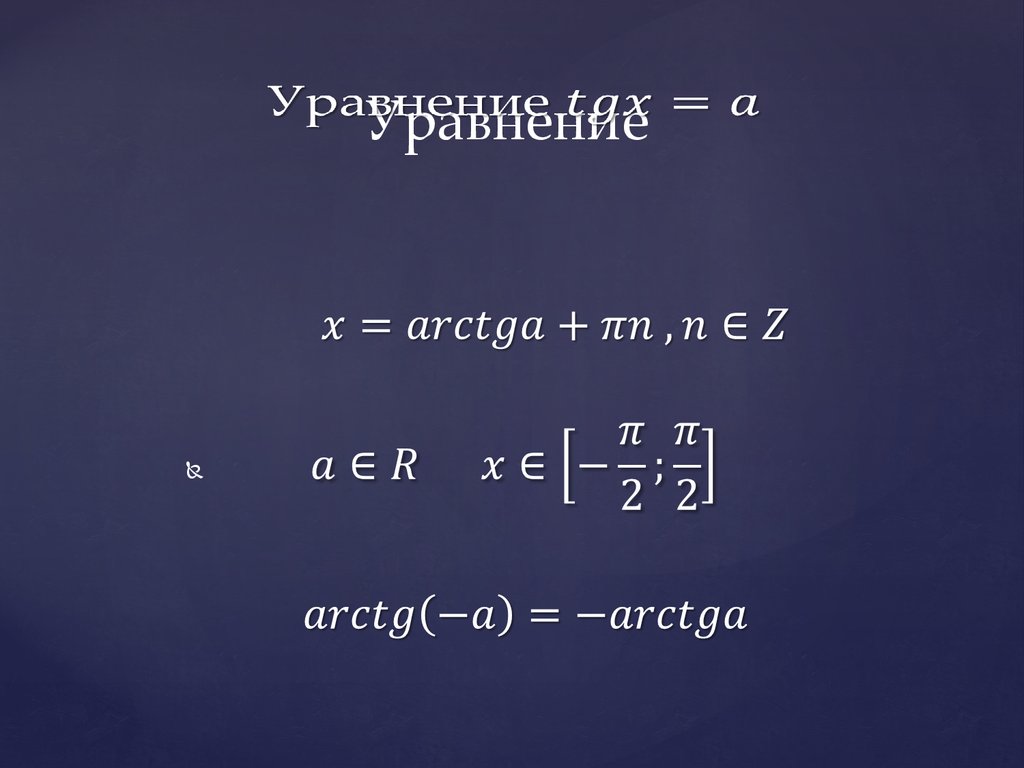









 Математика
Математика








