Деформация растяжения

1. Деформация растяжения

Деформация, при которой в поперечном сечении бруса возникает один
силовой фактор—продольная сила N, называется растяжением (сжатием).
Продольной силой N называется равнодействующая внутренних сил,
распределенных по площади поперечного сечения (нормальных напряжений):
N
dA
A
При равномерном распределении нормальных напряжений :
N A
Правило знаков: растягивающая продольная сила считается положительной,
а сжимающая– отрицательной.
Сущность метода сечений заключается в том, что величина продольной
силы в сечении стержня равна сумме всех внешних продольных сил
приложенных по одну из сторон от выбранного сечения.
y
II
I
F =10 кН, F =15 кН, F =55 кН, F =30 кН;
1
F2
F1
A
x
F4
E
F3
C
B
I
D
F5
K
2
3
Определим продольные силы в
z сечениях I-I и II-II.
II
N1-1= -F1-F2= -10-15= -25 кН,
4
N11-11= -F1-F2+F3= -10-15+55=30 кН.

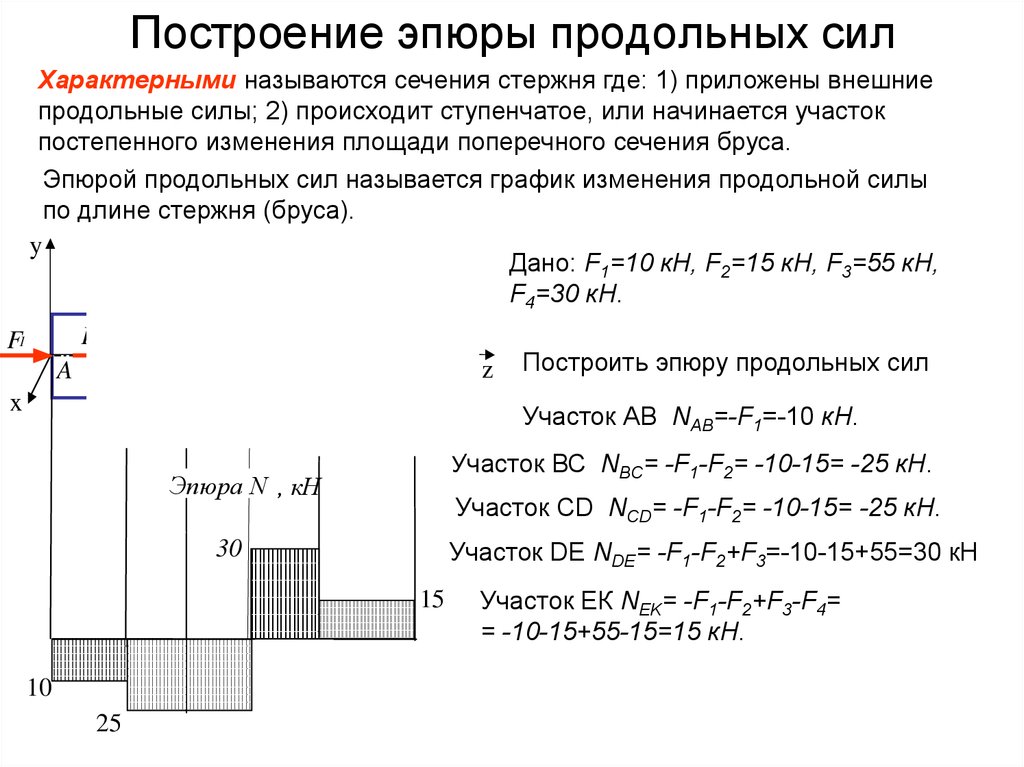
2. Построение эпюры продольных сил

Характерными называются сечения стержня где: 1) приложены внешние
продольные силы; 2) происходит ступенчатое, или начинается участок
постепенного изменения площади поперечного сечения бруса.
Эпюрой продольных сил называется график изменения продольной силы
по длине стержня (бруса).
y
Дано: F1=10 кН, F2=15 кН, F3=55 кН,
F4=30 кН.
F2
F1
A
F3
B
C
F5
F4
D
E
K
x
z
Построить эпюру продольных сил
Участок АВ NАВ=-F1=-10 кН.
Участок ВС NВС= -F1-F2= -10-15= -25 кН.
Эпюра N , кН
Участок CD NCD= -F1-F2= -10-15= -25 кН.
Участок DE NDE= -F1-F2+F3=-10-15+55=30 кН
30
15
10
25
Участок ЕК NEK= -F1-F2+F3-F4=
= -10-15+55-15=15 кН.

3. Построение эпюры продольных сил

Правила контроля эпюры продольных сил
Основные правила контроля правильности построения эпюры
продольных сил можно сформулировать так:
1. В сечении, где приложена сосредоточенная сила F, эпюра
продольных сил делает скачок на величину этой силы и с ее знаком.
2. Изменение площади поперечного сечения стержня влияния на
эпюру продольных сил не оказывает, независимо от характера этого
изменения (ступенчатое или постепенное).
3. На участке, где приложена равномерно распределенная нагрузка
эпюра продольных сил имеет вид прямой наклонной линии.

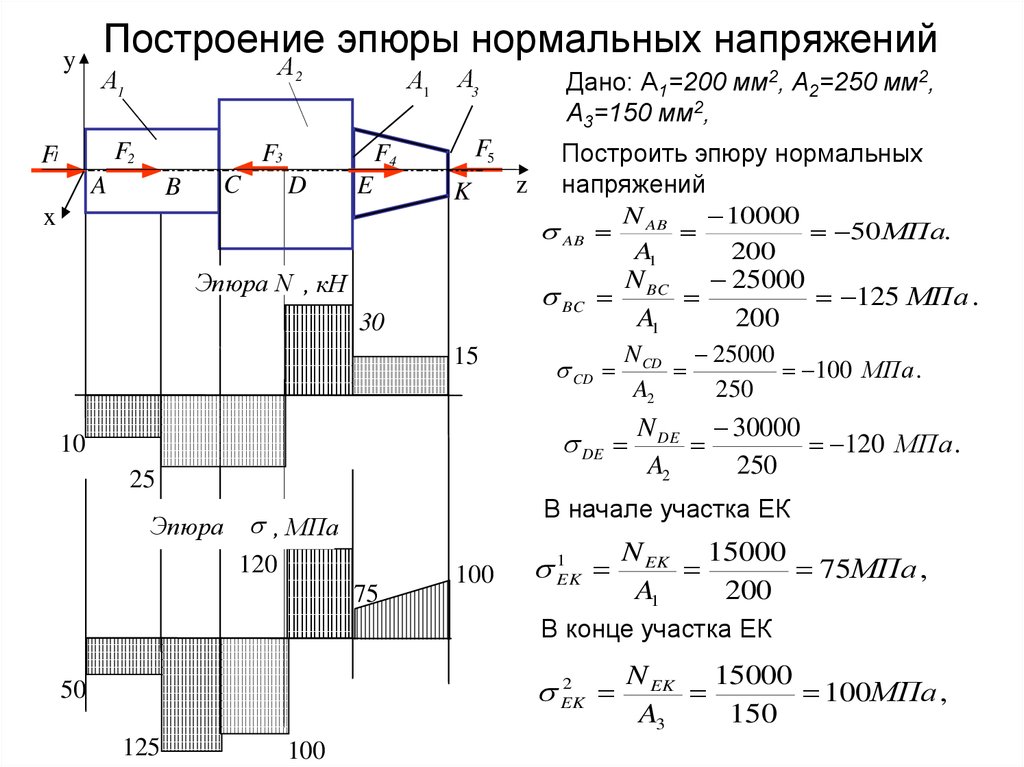
4. Построение эпюры нормальных напряжений

y
Построение эпюры нормальных напряжений
А2
А1
F2
F1
А1
F3
A
B
C
А3
F5
F4
D
E
K
x
Эпюра N , кН
30
15
Дано: А1=200 мм2, А2=250 мм2,
А3=150 мм2,
Построить эпюру нормальных
z напряжений
N
10000
AB AB
50 МПа.
A1
200
N
25000
BC BC
125 МПа .
A1
200
N
25000
CD CD
100 МПа .
A2
250
DE
10
25
N DE 30000
120 МПа .
A2
250
В начале участка ЕК
Эпюра , МПа
120
75
100
1EK
N EK 15000
75МПа ,
A1
200
В конце участка ЕК
2
EK
50
125
100
N EK 15000
100МПа ,
A3
150

5. Деформация растяжения

Правила контроля эпюры нормальных напряжений
Основные правила контроля правильности построения эпюры
нормальных напряжений можно сформулировать так:
1. На участке или в сечении стержня, где происходит изменение
площади поперечного сечения, нормальные напряжения изменяются
обратно пропорционально изменению площади, если площадь
изменяется ступенчато, то на эпюре наблюдается скачок, если
площадь изменяется постепенно, то эпюра имеет вид прямой
наклонной линии
2. В сечении, где приложена сосредоточенная сила эпюра нормальных
напряжений, делает скачок на величину пропорциональную силе и с
ее знаком.
3. На участке, где приложена равномерно распределенная нагрузка
эпюра нормальных напряжений имеет вид прямой наклонной линии

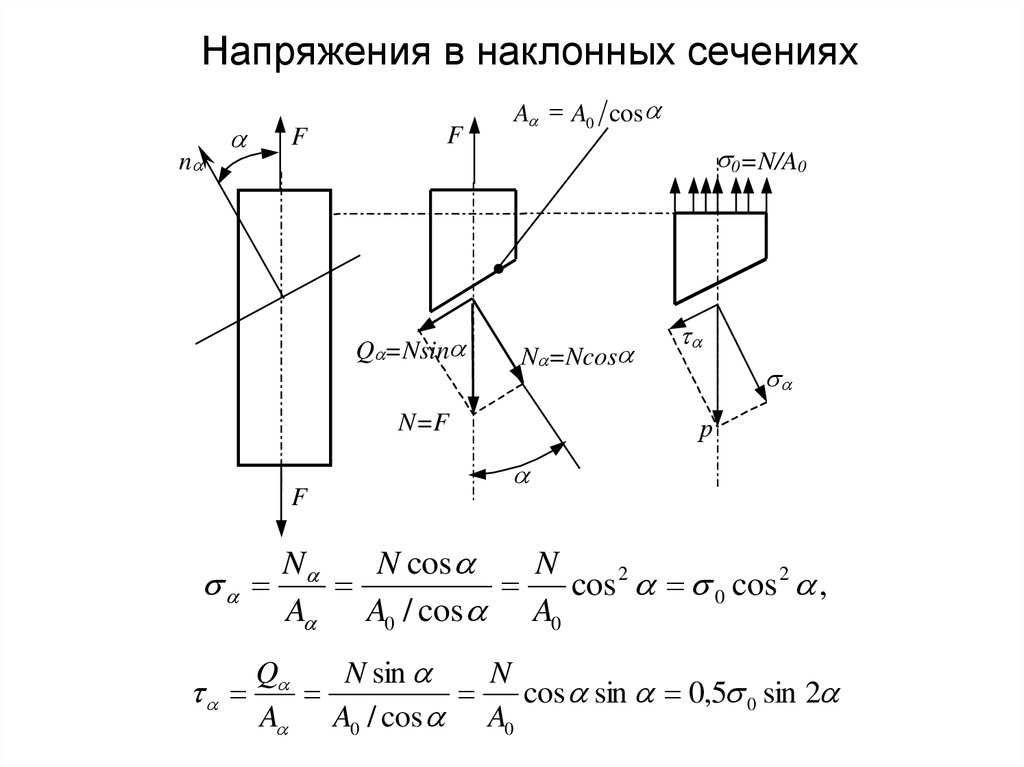
6. Напряжения в наклонных сечениях

n
F
F
Q =Nsin
A A0 cos
0=N/A0
N =Ncos
N=F
F
t
р
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
t
cos sin 0,5 0 sin 2
A A0 / cos A0

7. Напряжения в наклонных сечениях

Знак нормального напряжения определяется знаком продольной силы,
то есть растягивающее напряжение положительно, сжимающее –
отрицательно.
Касательное напряжение считается положительным, если изображающий
его вектор стремится вращать тело относительно любой точки, лежащей
на внутренней нормали к сечению по часовой стрелке.
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
t
cos sin 0,5 0 sin 2
A A0 / cos A0
Наибольшие нормальные напряжения (по абсолютной величине)
действуют в поперечном сечении стержня.
Наибольшие касательные напряжения действуют в сечениях
наклоненных под углом в 45о к оси стержня.
Касательные напряжения в поперечном сечении стержня равны нулю.

8. Закон Гука

Закон Гука имеет два аналитических выражения— через относительные, и
через абсолютные величины
В относительных величинах
В абсолютных величинах
Nl
l
EA
E
Жесткостью поперечного сечения стержня называют произведение площади
поперечного сечения А на модуль продольной упругости материала Е:
Сп.с. АЕ
Способность стержня сопротивляться деформированию оценивают величиной
относительной жесткости стержня, которая равна отношению жесткости
поперечного сечения ЕА к длине стержня l:
С
АЕ
l
Податливость стержня:
l
EA

9. Деформации и перемещения

lк
l0
Деформации и перемещения
l lк l0 ,
Относительной продольной деформацией
называется отношение абсолютной продольной
деформации l к первоначальной длине стержня l0:
l
F
l l0
b
b0
Величина, на которую изменится длина бруса
(или одного из его участков) под действием
продольных сил, называется продольной
деформации
b/2
a
a0
a/2
Величина а ( b), на которую изменится размер
поперечного сечения бруса а0 (b0) под действием
продольной силы, называется поперечной
деформацией.
Отношение абсолютной поперечной деформации, а ( b) к первоначальному
размеру сечения бруса а0 (b0), называется относительной поперечной
деформаций:
а/
a
,
a0
b/
b
b0

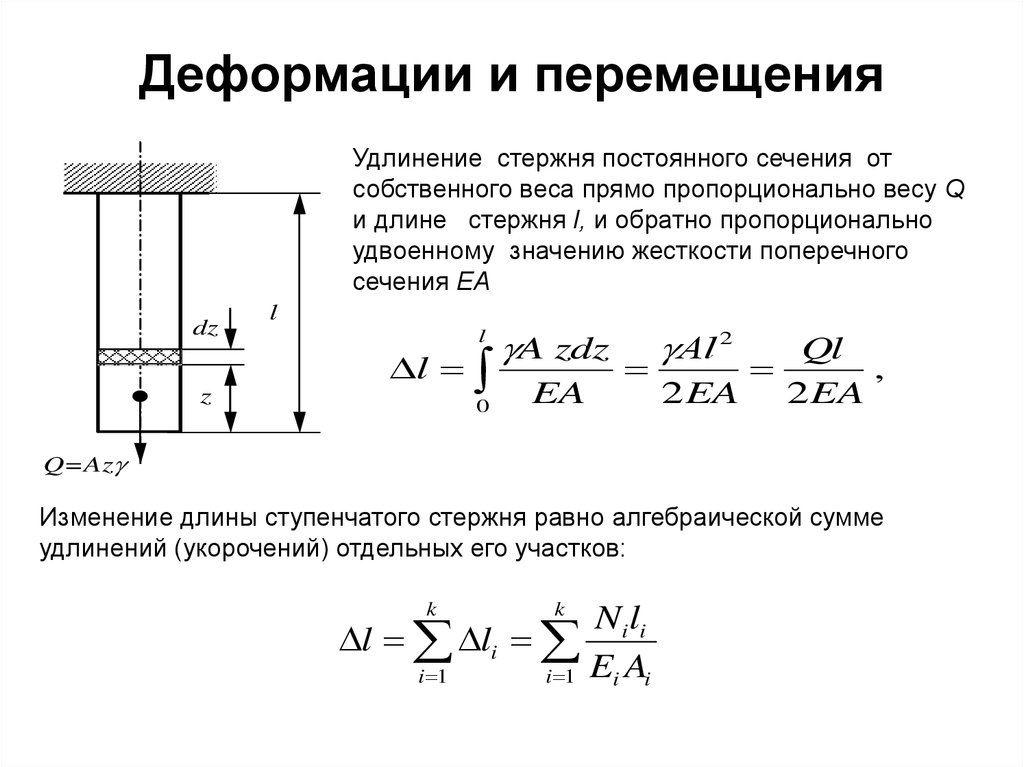
10. Деформации и перемещения

Удлинение стержня постоянного сечения от
собственного веса прямо пропорционально весу Q
и длине стержня l, и обратно пропорционально
удвоенному значению жесткости поперечного
сечения EA
dz
l
l
l
z
0
A zdz
EA
Аl 2
2 EA
Ql
,
2 EA
Q=Az
Изменение длины ступенчатого стержня равно алгебраической сумме
удлинений (укорочений) отдельных его участков:
k
k
N i li
l li
i 1
i 1 Ei Ai

11. Деформации и перемещения

а
a/2
0
b
Длина участков а=1,2 м, b=0,8 м, c=1 м;
Модуль упругости Е=2·105 МПа;
Площадь сечения участков стержня:
А1 =20 см2, А2 =40 см2, А3 =15 см2;
Продольная сила F=50 кН.
Удлинения участков бруса
Fa
50 103 1,2
l1
1,5 10 4 м;
11
4
EA1 2 10 20 10
c
c/2
I
II
F
0
I
II
A1
A2
A3
Fb
50 103 0,8
4
l2
0
,
5
10
м;
11
4
EA2 2 10 40 10
Эпюра l
lI-II
l0-II
l
Fc
50 103 1,0
4
l3
1
,
67
10
м
11
4
EA3 2 10 15 10
Полное удлинение стержня:
l l1 l2 l3 1,5 10 4 0,5 10 4 1,67 10 4 3,67 10 4 м
Перемещение сечения 1I-I1 относительно заделки:
lI II l1 2 l2 l3 2 1,5 10 4 2 0,5 10 4 1,67 10 4 2 2,085 10 4 м
Перемещение сечения II относительно сечения I:
l0 II l1 l2 l3 2 1,5 10 4 0,5 10 4 1,67 10 4 2 2,835 10 4 м

12. Коэффициент Пуассона

Отношение относительной поперечной деформации º / к относительной
продольной деформации º взятое по модулю, называется коэффициентом
Пуассона:
/
Коэффициент Пуассона принимает значения в пределах от 0 до 0,5 и
определяется экспериментально. Меньшее значение коэффициента имеют
бетон – 0,16…0,18, стекло – 0,25, большие значения каучук – 0,48, свинец –
0,42, целлулоид – 0,38. У большинства материалов используемых в
машиностроении =0,24…0,36.
Коэффициентом изменения объёма называется безразмерная величина
представляющая собой отношение величины, на которую изменяется объём
бруса при деформации V=Vк-V0 к его первоначальному объёму V0
/
kV 2 1 2 1 2 .
/
a
/
b
/
Коэффициент изменения объема принимает следующие значения: при
сжатии объём бруса уменьшается и kV<0, при растяжении объём
увеличивается и kV>0. Для материалов с коэффициентом Пуассона
0,5 изменение объёма не происходит и kV 0

13. Допускаемые напряжения

Опасным называется напряжение 0 при котором конструкция становится
не работоспособной.
Для конструкций из пластичных материалов основной причиной потери
работоспособности являются большие пластические деформации и в этом
случае опасное напряжение равно физическому пределу текучести: 0 = т.
Для пластичных не имеющих физического предела текучести, опасное
напряжение приравнивается к условному пределу текучести: 0 = 0,2.
Для конструкций из хрупких материалов основной причиной потери
работоспособности является разрушение, которое происходит, как правило,
без видимых остаточных деформаций. И в качестве опасного напряжения
принимают предел прочности пч или временное сопротивление разрыву вр.
Под коэффициентом запаса прочности понимают величину,
указывающую во сколько раз необходимо уменьшить опасное напряжение
0 , чтобы прочность конструкции или детали, в заданных условиях
эксплуатации, была гарантирована, а максимальные напряжения, в любом
случае, не превышали предела пропорциональности пц .
Величину коэффициента запаса прочности для пластичных материалов
рекомендуется выбирать из интервала SТ = 1,25-2,5.
Коэффициент запаса прочности для хрупких материалов, изменяется в
пределах Sвр = 2,4 – 5,0.

14. Допускаемые напряжения

Допускаемыми называются наибольшие напряжения, которые можно
допустить в рассчитываемой конструкции из условий ее безопасной,
надежной и долговечной работы.
т
sт
0
0 , 2
S
sт
в р
sв р
для пластичных материалов
для пластичных материалов не
имеющих физического предела
текучести
для хрупких материалов
Пластические свойства материалов оцениваются величиной относительного
остаточного удлинения .
Для оценки приняты следующие условия:
•если <5 % материал считается хрупким;
•если 5 % < < 10 % - хрупко—пластичным;
•если > 10 % - пластичным.

15. Расчеты на прочность при растяжении

Расчётными называются напряжения вычисленные по теоретическим или
экспериментальным формулам для конкретной конструкции с учетом величины
приложенных к ней внешних нагрузок, размеров и формы ее элементов.
F
A
Условие прочности формулируется так нормальные расчетные напряжения в
любом сечении растянутого (сжатого) стержня не должны превышать
допускаемого значения:
Из условия прочности при растяжении (сжатии) вытекают следующие задачи:
1. Задача проверочного расчета
2. Задача проектного расчета.
F
A
A
F
3. Задача определения максимальной допускаемой грузоподъемности
F A