Теория игр и принятие решений

1.

Тема «Теория игр и
принятие решений»

2. Учебные вопросы:

1. Предмет и задачи теории игр.
2. Матричные игры. Равновесная ситуация.
3. Смешанные стратегии матричных игр.
4. Игры с природой.

3. 1. Предмет и задачи теории игр.

Построением математических моделей конфликтных ситуаций и разработкой
методов решения возникающих в этих ситуациях задач занимается теория игр.
Методы
и
рекомендации
теории
игр
повторяющимся
конфликтным
ситуациям.
применимы
Если
к
многократно
конфликтная
ситуация
реализуется ограниченное число раз, то рекомендации теории игр теряют смысл.
Игра – это упрощенная математическая модель конфликтной ситуации.
Игра ведется по определенным
правилам. Суть игр состоит в том, что
каждый участник принимает такое решение, которое, как он полагает, обеспечит
ему наилучший исход. Исходом игры называется значение некоторой функции,
называемой функцией выигрыша (платежной функцией), которая может
задаваться в матричном или аналитическом виде.

4. 1. Предмет и задачи теории игр.

Стратегия
–
последовательность
это
совокупность
действий
игрока
правил,
в
однозначно
каждой
определяющих
конкретной
ситуации,
складывающейся в процессе игр.
Оптимальной называется стратегия, которая при многократном повторении
игры обеспечивает данному игроку максимально возможный средний выигрыш.
Количество стратегий у каждого игрока может быть конечным или бесконечным.
В зависимости от этого игры подразделяются на конечные и бесконечные.
Игра состоит из отдельных партий.
Партия – это каждый вариант реализации игры.
В партии игроки совершают ходы.
Ход – это выбор и реализация игроком одного из допустимых вариантов
поведения.

5. 2. Матричные игры:

Пусть в игре участвуют два игрока. Игрок А имеет m
стратегий, а игрок В – n стратегий.
Обозначим стратегии игрока А как А1,А2,…,Аm , а
стратегии игрока В – как В1 ,В2 …,Вn .
Если игрок А выбрал стратегию Ai , а игрок B –
стратегию Bk , то выигрыш игрока A составит аik , а игрока
B – bik , причем
аik = - bik (1)

6. 2. Матричные игры:

Поэтому при анализе такой игры достаточно рассмотреть выигрыш
только одного игрока, например выигрыш аik игрока А. Зная выигрыш
аik по формуле (1) легко определить выигрыш bik .
Матричные игры называются парными играми с нулевой суммой, в
которых выигрыш одного игрока равен проигрышу другого.
Если известны все значения аik для каждой пары стратегий {Ai Bk },
i =1, 2, …, m, k = 1, 2, …, n, то их удобно записать в виде
прямоугольной таблицы, строки которой соответствуют стратегиям
игрока A , а столбцы – стратегиям игрока В (табл. 1).

7. 2. Матричные игры:

:
2. Матричные игры:
Таблица 1.
A1
A2
…
Am
B1
B2
а11
a12
а21
а22
…
…
аm1
аm2
…
…
…
…
…
Bn
а1n
а2n
…
аmn
Чаще эти выигрыши записывают в виде платежной матрицы (матрицы игр)
размера , поэтому такие игры называются матричными играми :
A=
a11
a 21
...
a
m1
a12
a 22
...
am 2
a1n
... a 2 n
... ...
... a mn
...
Чаще
выигр

8. 2. Матричные игры:

Равновесная ситуация
Пусть матричная игра m×n задана платежной матрицей
A=
a11
a21
...
a
m1
a12
a22
...
am 2
a1n
... a2 n
... ...
... amn
...
(2)
Строки этой матрицы соответствуют стратегиям игрока , а
столбцы – стратегиям игрока . В теории игр предполагается,
что оба игрока действуют разумно, т.е. стремятся к
получению максимального выигрыша, считая, что соперник
действует наилучшим для себя образом.

9. 2. Матричные игры:

Определим оптимальные стратегии каждого из игроков.
Начнем с анализа стратегий игрока А . На стратегию Аi игрока
A игрок B ответит такой стратегией Bk, при которой выигрыш
игрока A будет минимальным. Аналогично игрок B будет
отвечать на все m стратегий игрока A . Другими словами,
найдем в каждой строке матрицы минимальный элемент
(минимальные выигрыши игрока A)
i min аik , i 1,2, , n
k
и запишем их в правом столбце табл. 2.

10. 2. Матричные игры:

Минимальные
выигрыши
игрока А
B1
В2
…
Вk
…
Bn
a11
a12
a1k
a1n
a22
a2 k
…
a21
a2 n
1
2
Ai
ai1
ai 2
aik
ain
i
am1
am 2
amk
amn
m
1
2
k
n
A1
A2
…
Am
Максимальные
выигрыши
игрока А
Действуя разумно, игрок остановится на той стратегии , для которой
окажется максимальным. Поэтому среди чисел выбираем максимальное
число
max i max min aik
i
i
k
(3)

11. 2. Матричные игры:

Принцип построения стратегии игрока А, основанный на
максимизации минимальных выигрышей, называется принципом
максимина (maxmin).
Проведем анализ стратегий игрока В. Для этого найдем в каждом
столбце матрицы максимальный элемент (максимальные выигрыши
aik , k 1, 2, , n
игрока А ): k max
i
И запишем их в нижней строке табл. 2. Действуя разумно, игрок B
aik
остановится на той стратегии k , для которой k max
i
выбираем минимальное число
k min k min max aik
k
k
(4)
i
Число β называется верхней ценой игры.

12. 2. Матричные игры:

Принцип построения стратегии игрока B, основанный на минимизации
максимальных выигрышей, называется принципом минимакса (minmax).
Нижняя цена игра α и верхняя цена игра β связаны неравенством
α ≤ β.
(5)
Если аi , opt, k , opt или
max min aik min max aik ai , opt, k , opt '
i
k
то ситуация
k
А
i , opt ,
Bk , opt
i
(6)
оказывается равновесной, и ни один игрок не
заинтересован в том, чтобы ее нарушить. В том случае, когда верхняя цена
игры равна нижней, их называют просто ценой игры.
Если α=β, то такую игру называют также игрой с седловой точкой, а
пара оптимальных стратегий Аi , opt, Вk , opt – седловой точкой матрицы. Цена
игры обозначается буквой v. Тогда . v аi , opt, k , opt

13. 3. Смешанные стратегии матричных игр

Если платежная матрица не имеет седловой точки, т.е.
, то поиск решения игры приводит к применению
сложной стратегии, состоящей в случайном применении
двух и более стратегий с определенными частотами. Такая
сложная стратегия называется смешанной.
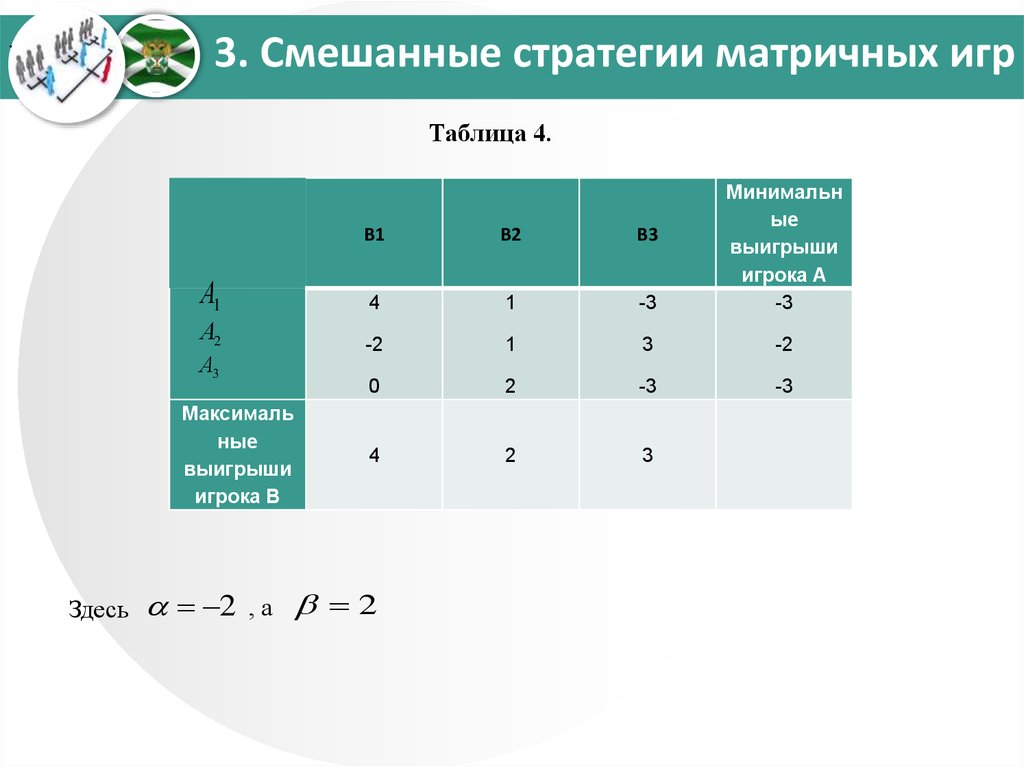
В табл. 4 приведен пример, когда нижняя цена игры
не совпадает с верхней ценой игры .

14. 3. Смешанные стратегии матричных игр

.
Таблица 4.
В1
В2
В3
А1
4
1
-3
Минимальн
ые
выигрыши
игрока А
-3
А2
-2
1
3
-2
0
2
-3
-3
4
2
3
А3
Максималь
ные
выигрыши
игрока В
Здесь
2
,а
2

15. 3. Смешанные стратегии матричных игр

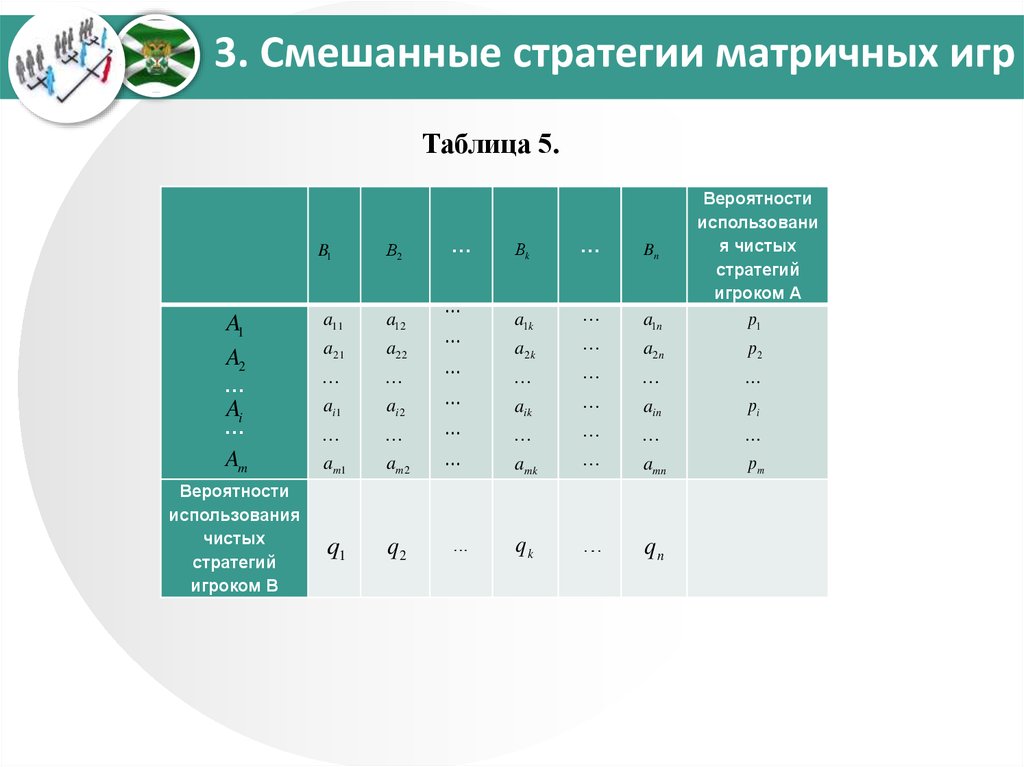
Обратимся к общему случаю матричной игры, представленной
в табл. 2. Обозначим через
вероятности, с которыми
игрок А использует в ходе игры свои чистые стратегии A , A ,..., A
1
2
m
Для этих вероятностей выполняются условия:
m
p
i 1
i
1; p1 0, p 2 0,..., p m 0
(8)
Вектор p p( p1 , p2 ,..., pm ) , проекция которого удовлетворяет
условиям (8), полностью определяет характер игры игрока А и
называется его смешанной стратегией. Механизм случайного
выбора чистых стратегий, которым пользуется игрок А,
обеспечивает
стратегий.
ему
бесконечное
множество
смешанных

16. 3. Смешанные стратегии матричных игр

Аналогично, вектор
q q(q1 , q2 ,..., qm )
, проекция которого
удовлетворяет условиям (9),
n
q
k 1
ki
1; q1 0, q 2 0,..., q n 0
(9)
полностью определяет характер игры игрока В и называется
смешанной стратегией игрока В. Игрок В, как и игрок А,
располагает
стратегий.
бесконечным
множеством
смешанных

17. 3. Смешанные стратегии матричных игр

Пусть игроки А и В применяют и
стратегии
p
смешанные
и q соответственно, т.е. игрок А использует
стратегию Ai с вероятностью p i , а игрок В – стратегию Bk с
вероятностью qk. Поскольку события
вероятность
произведению
появления
и
независимы, то
комбинации ( Ai , Bk )
вероятностей
и
равна
, т.е. . При
использовании смешанных стратегий игра приобретает
случайный характер, случайными становятся и величины
выигрышей игроков.

18. 3. Смешанные стратегии матричных игр

Поэтому выигрыш игрока А (проигрыш игрока В)
определяют
его
математическим
рассчитываемым по формуле
ожиданием,
(10)
Функция (10) называется платежной функцией игры с
матрицей, заданной в табл. 5.
Нижней ценой игры называется число
по формуле:
(11)
Верхней ценой игры называется число
по формуле:
, рассчитываемое
(12)
, рассчитываемое

19. 3. Смешанные стратегии матричных игр

Таблица 5.
B1
В2
…
Вk
…
Bn
Вероятности
использовани
я чистых
стратегий
игроком А
a1k
a1n
p1
a2 k
a2 n
p2
aik
ain
pi
a11
a12
a21
a22
…
Ai
…
ai1
ai 2
Am
am1
am 2
amk
amn
pm
q1
q2
qk
qn
A1
A2
Вероятности
использования
чистых
стратегий
игроком В

20. 3. Смешанные стратегии матричных игр

Оптимальными
смешанными
стратегиями
называются
стратегии,
удовлетворяющие соотношению (сравнить с формулой (6)).
max min E A, p, q min max E A, p, q E A, p opt , q opt . (13)
p
q
q
p
определенную соотношением
Величину
(13), называют ценой игры.
Векторы
p opt
и
q opt
называются
оптимальными
смешанными
стратегиями, если они образуют седловую точку платежной функции игры
E A, p, q
, т.е. удовлетворяют неравенству (сравнить с неравенством (7))
E A, p, q E A, p , q E A, p , q . (14)
opt
opt
opt
opt
Из соотношения (14) следует, что в седловой точке ( p opt , q opt ) платежная
функция E A, p, q достигает максимума по смешанным стратегиям p игрока А
и минимума по смешанным стратегиям q игрока В.

21. 3. Смешанные стратегии матричных игр

Теорема 1. Основная теорема теории матричных игр. (Дж. фон
Нейман).
Для матричной игры с любой матрицей А величины max min E A, p, q и
p
q
min max E A, p, q существуют и равны между собой:
q
p
max min E A, p, q min max E A, p, q .
p
q
q
p
Более того, существует хотя бы одна ситуация в смешанных стратегиях
( p opt , q opt ) , для которой выполняется соотношение
E ( A, p opt , q opt ) max min E A, p, q min max E A, p, q
p
q
q
p
.

22. 3. Смешанные стратегии матричных игр

Пусть
p opt p opt ( p1,opt , p2,opt ,..., pm,opt )
q opt q opt (q1,opt , q2,opt ,..., qn,opt )
,
оптимальные смешанные стратегии и
Оптимальная
смешанная
-
v E ( A, p opt , q opt ) - цена игры.
стратегия
складывается только из тех чистых стратегий
игрока
А
, i 1,2,..., m
(т.е. только те вероятности , могут отличаться от нуля),
n
для которых aik q k ,opt
v
k 1
Аналогично, только те вероятности
отличаться от нуля, для которых a
, k 1,2,..., n
m
i 1
ik
p i ,opt v
могут

23. 3. Смешанные стратегии матричных игр

Графические решения матричных игр
Графический метод применим к тем играм, в которых
хотя бы один игрок имеет две стратегии.
Рассмотрим игру 2×п, представленную в табл. 6. Эта
игра не имеет седловой точки. Согласно теореме имеем
2
v min aik Pi , opt min (a1k Popt a2 k (1 popt ))
1 k n
1 k n
i 1
max min( a
1k
p
p a2k (1 p))
1 k n
(15)

24. 3. Смешанные стратегии матричных игр

Максимум функции
min
(a1k p a2k (1 p))
1 k n
(16) найдем,
построив ее график. Для этого поступаем следующим образом. Построим графики прямых
w k =а 1 k p + a 2 k (1 -p )= ( a 1 k -a 2 k )p + a2k
(17)
для каждого к = 1, 2,..., п в системе координат pOw (рис.1). В
соответствии с требованием (16) на каждой из построенных
прямых определяются и отмечаются наименьшие значения. На
рис. 2 эти значения выделены полужирной ломаной линией. Эта
ломаная огибает снизу все семейство построенных прямых и
называется нижней огибающей семейства.

25. 3. Смешанные стратегии матричных игр

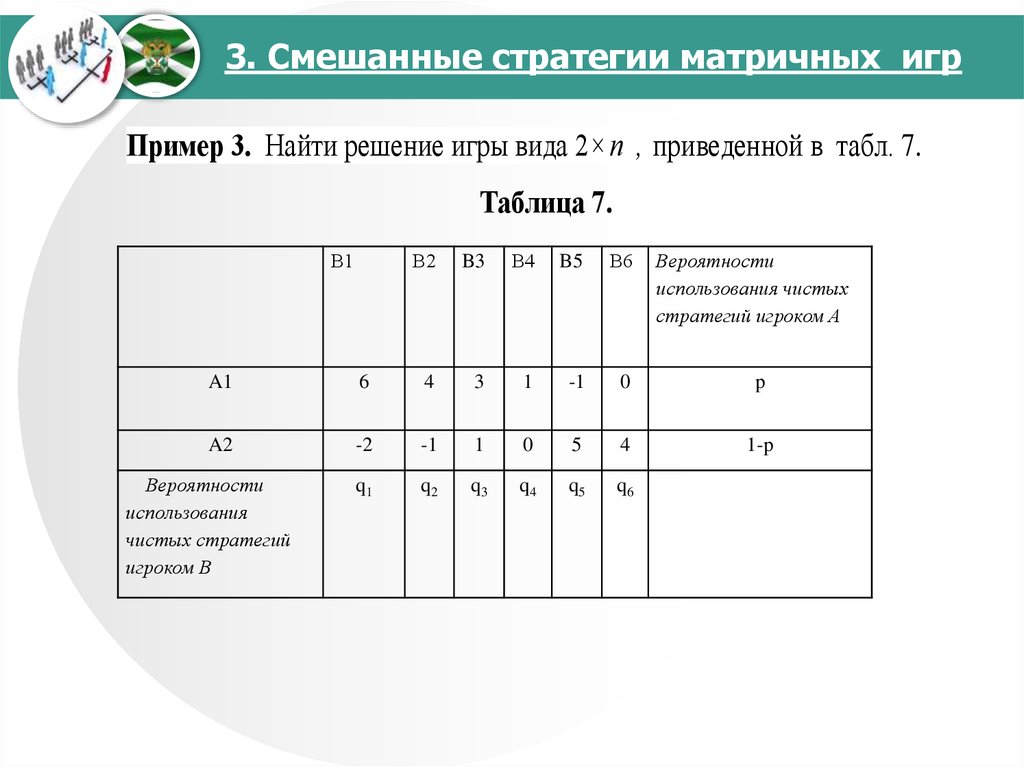
Пример 3. Найти решение игры вида 2×п , приведенной в табл. 7.
Таблица 7.
В1
В2
B3
В4
B5
В6
Вероятности
использования чистых
стратегий игроком А
A1
6
4
3
1
-1
0
p
A2
-2
-1
1
0
5
4
1-p
q1
q2
q3
q4
q5
q6
Вероятности
использования
чистых стратегий
игроком В

26. 3. Смешанные стратегии матричных игр

Р е ш е н и е . Проведем анализ игры на наличие седловой точки.
Нижняя цена игры равна -1, верхняя равна 1. Седловой точки нет. Решение
надо искать в смешанных стратегиях.
Построим график нижней огибающей (16). Предварительно запишем
уравнения прямых (17):
w1 6 p 2(1 p ) 8 p 2;
w2 4 p 1 (1 p ) 5 p 1;
w3 3 p (1 p ) 2 p 1;
w4 p 0 (1 p ) p;
w5 p 5 (1 p ) 6 p 5;
w6 0 p 4(1 p ) 4 p 4.

27. 3. Смешанные стратегии матричных игр

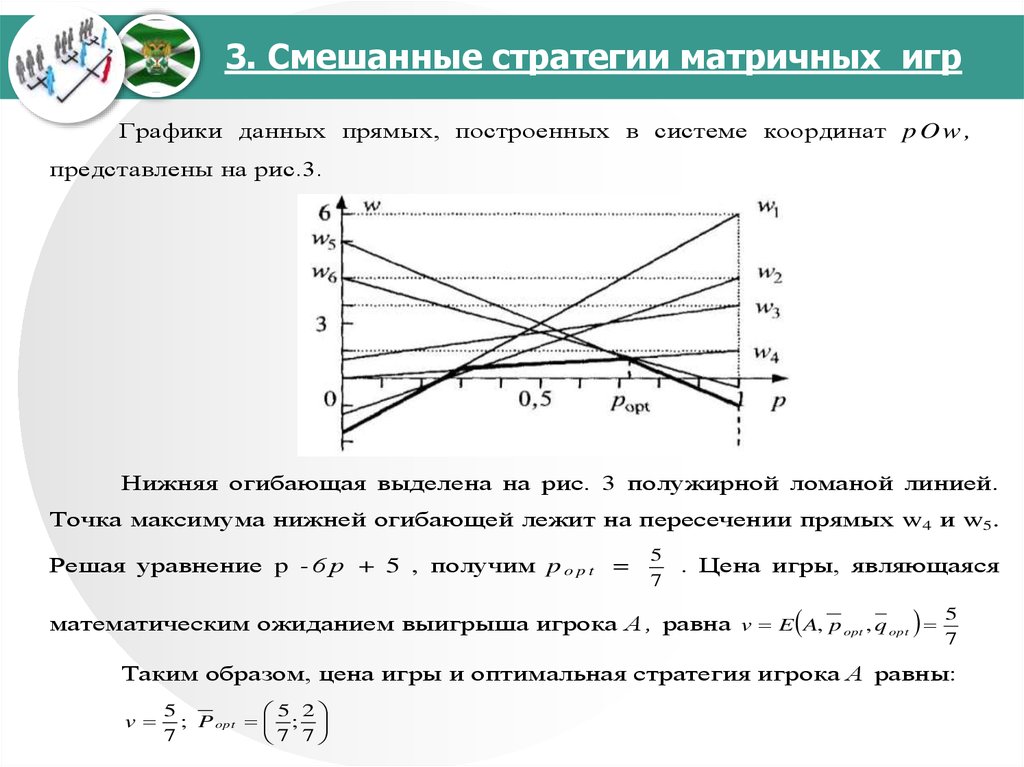
Графики данных прямых, построенных в системе координат p O w ,
представлены на рис.3.
Нижняя огибающая выделена на рис. 3 полужирной ломаной линией.
Точка максимума нижней огибающей лежит на пересечении прямых w4 и w5.
Решая уравнение p - 6 р + 5 , получим p o p t =
5
7
. Цена игры, являющаяся
математическим ожиданием выигрыша игрока А , равна v E A, p opt , q opt
5
7
Таким образом, цена игры и оптимальная стратегия игрока А равны:
v
5
5 2
; P opt ;
7
7 7