Преобразование выражений

1. Дискретная математика

2.

Преобразование выражений
Любую формулу можно
преобразовать к ДНФ.
1) Заменить все знаки функций на знаки
булевых функций (конъюнкция (˄),
дизъюнкция (˅) и отрицание (¬)),
используя тождества.
2) По закону де Моргана и двойного
отрицания опустить отрицание до
переменных.
3) По закону дистрибутивности раскрыть
скобки.

3.

Преобразование выражений
4) Уменьшить число конъюнкций,
пользуясь законами поглощения,
склеивания, уничтожения кратности,
свойствами констант.
5) Уменьшить число элементов в
конъюнциях, пользуясь законом
уничтожения кратности, свойствами
констант.
Получим ДНФ.

4. Приведение к ДНФ

F ( x , y , z ) xy x yz x y
8
xy x yz x y
15
x y x y z x y
5
x y x y z x y

5. Приведение к ДНФ

12
x x x y x z xy yy yz x y
1,3
x y x z xy yz x y
26
x y yz x z xy x y
3
x y yz xy x y

6. Приведение к ДНФ

5
x y yz xy x y
10 ,12
x y x y yz x y xy x y
16 ,17
x y x z 0 0 x y.

7. Переход от ДНФ к КНФ

1) Пусть функция f задана в виде
ДНФ.
F k1 k2 ... kn
Здесь
k1 , k2 , ..., kn
–
элементарные конъюнкции.

8. Переход от ДНФ к КНФ

2) Применим закон двойного
отрицания F F .
3) Приведем к ДНФ
F
.
F k1 k2 ... kn k1 k2 ... kn
d1 d 2 ... d n k1 k2 ... kn
Здесь d1 , d 2 , ..., d n – элементарные
дизъюнкции.

9. Переход от ДНФ к КНФ

4) Возьмем второе отрицание над F.
Во время преобразования не будем
раскрывать скобки – остановимся на
формуле, имеющей вид конъюнкции
элементарных дизъюнкций – КНФ.
F F k1 k2 ... kn
k1 k2 ... kn
d1 d 2 ... d n

10. Правило получения СКНФ из вектор-столбца

1) Выбрать все нулевые наборы значений
аргументов.
2) Каждому нулевому набору поставить в
соответствие элементарную дизъюнкцию
всех переменных так, чтобы в дизъюнкции
переменная была с отрицанием, если в
наборе она равна 1.
3) Соединить полученные элементарные
дизъюнкции знаком конъюнкции.

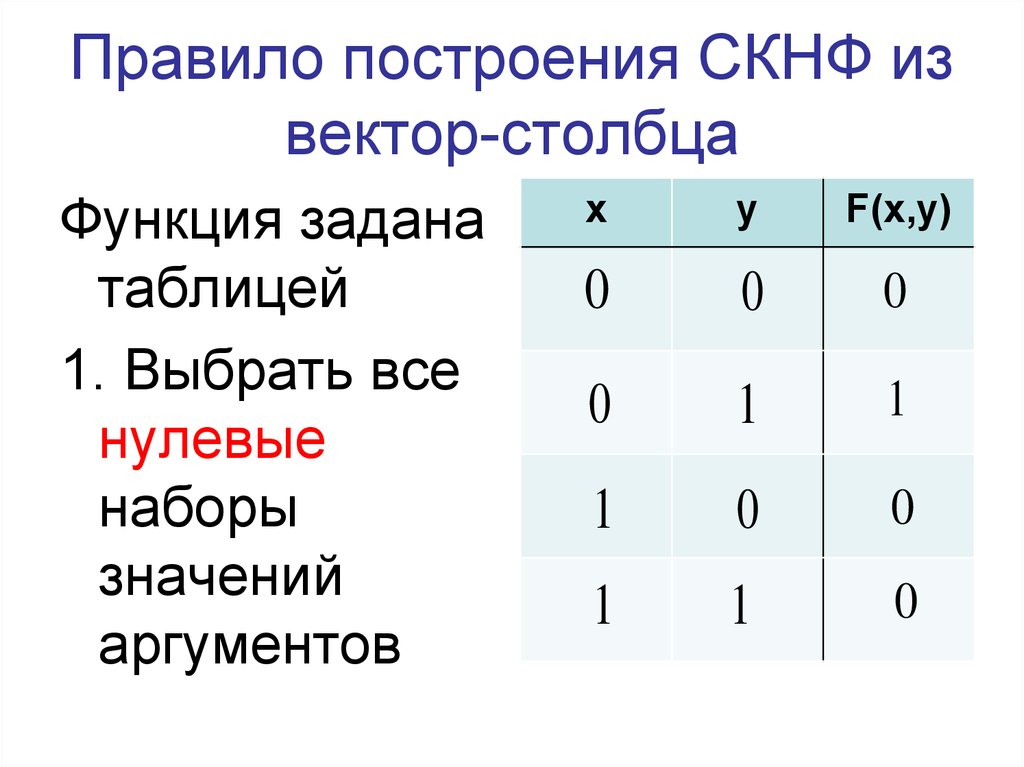
11. Правило построения СКНФ из вектор-столбца

Функция задана
таблицей
1. Выбрать все
нулевые
наборы
значений
аргументов
х
у
F(x,y)
0
0
0
0
1
1
1
0
0
1
1
0

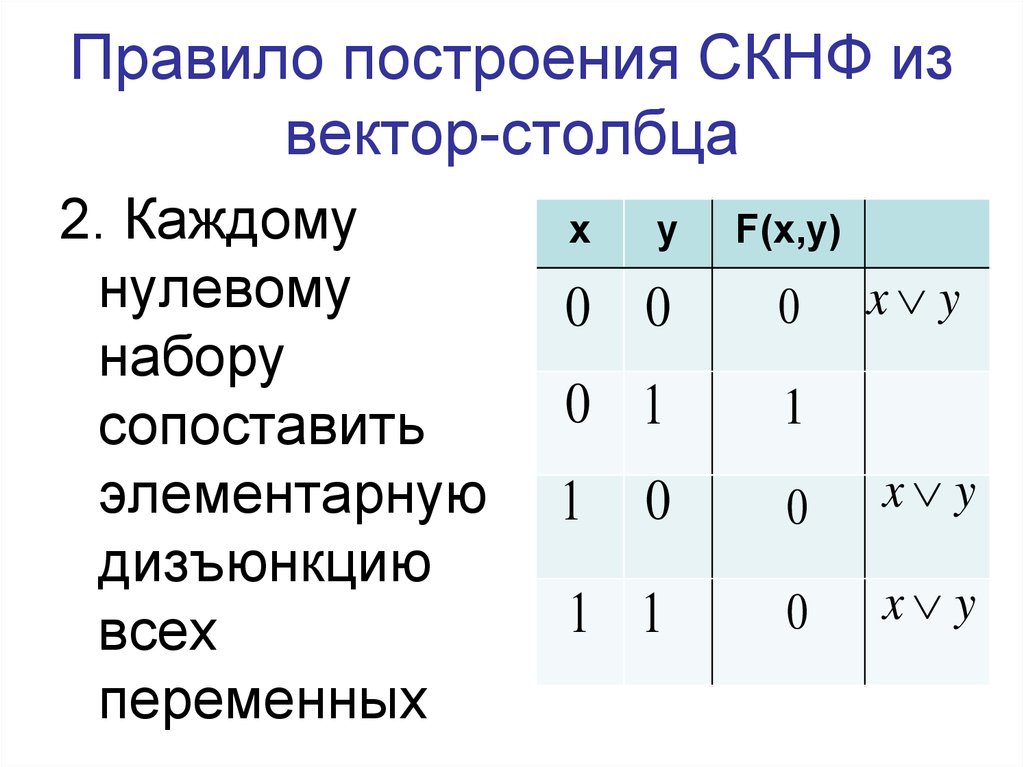
12. Правило построения СКНФ из вектор-столбца

2. Каждому
нулевому
набору
сопоставить
элементарную
дизъюнкцию
всех
переменных
х
у
F(x,y)
x y
0 0
0
0 1
1
0
0
x y
1 1
0
x y
1

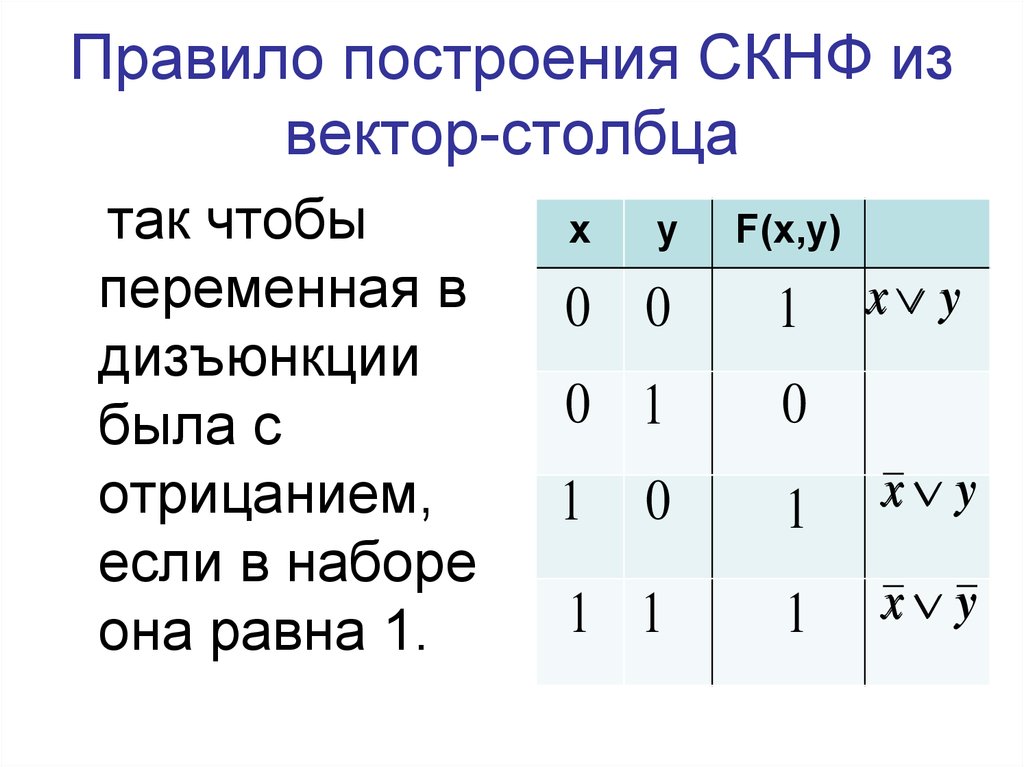
13. Правило построения СКНФ из вектор-столбца

так чтобы
переменная в
дизъюнкции
была с
отрицанием,
если в наборе
она равна 1.
х
у
F(x,y)
0 0
1
0 1
0
x y
0
1
x y
1 1
1
x y
1

14. Правило построения СКНФ из вектор-столбца

3. Соединить полученные
дизъюнкции знаком
конъюнкции
x y x y x y