Похожие презентации:
Лэмбовский сдвиг иона мюонного гелия
1. Лэмбовский сдвиг иона мюонного гелия
<<САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ>>Лэмбовский сдвиг иона
мюонного гелия
Выполнил:
студент 3 курса группы 03.301.50
Физического факультета СамГУ
кафедры общей и теоретической физики
Мухатаев Д.В.
Проверил: Мартыненко А.П.
д.ф.м.н
Самара 2015
2. Содержание
1. Введение2. Эксперимент Лэмба и Резерфорда
3. Нерелятивистская теория
4. Заключение
5. Список литературы
3. Введение
• Развитие техники радиоспектроскопии атомов и молекул привело крезкому увеличению точности измерения тонкой и сверхтонкой
структур в спектрах атомов и молекул. Одной из самых интересных
задач, которую можно было поставить благодаря такому увеличению
точности, была проверка релятивистского волнового уравнения для
одного электрона (уравнения Дирака).
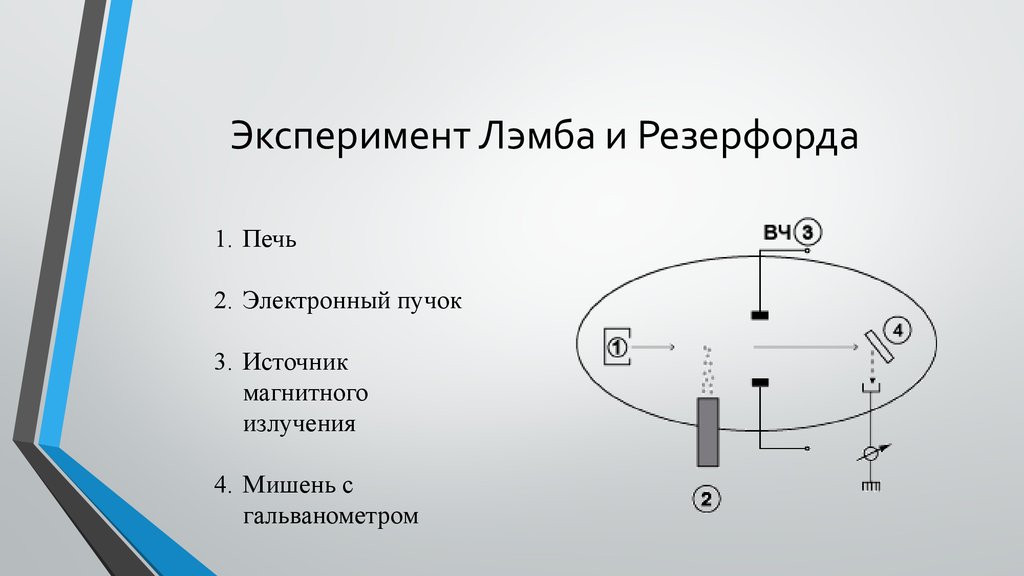
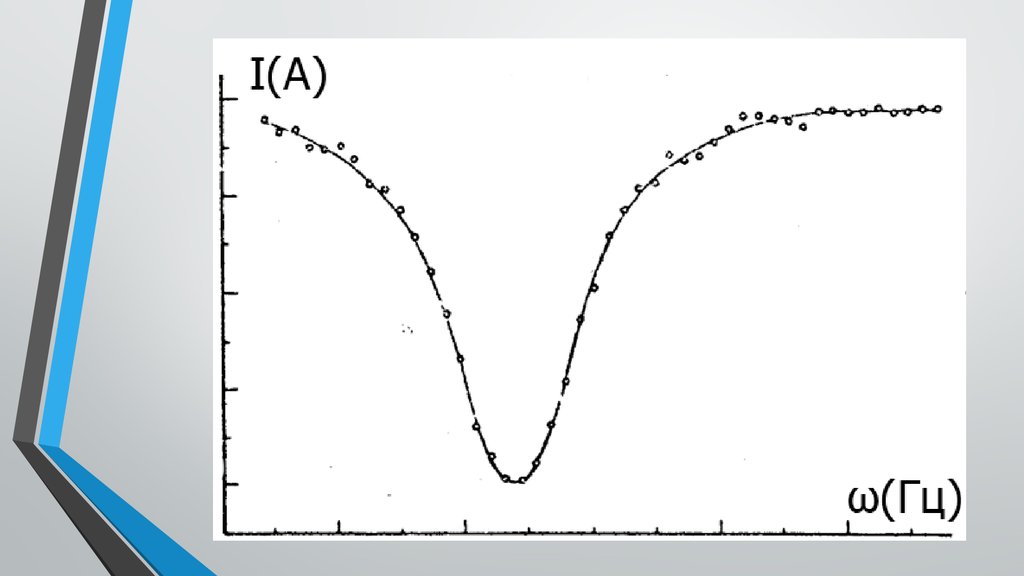
4. Эксперимент Лэмба и Резерфорда
1. Печь2. Электронный пучок
3. Источник
магнитного
излучения
4. Мишень с
гальванометром
5.
6.
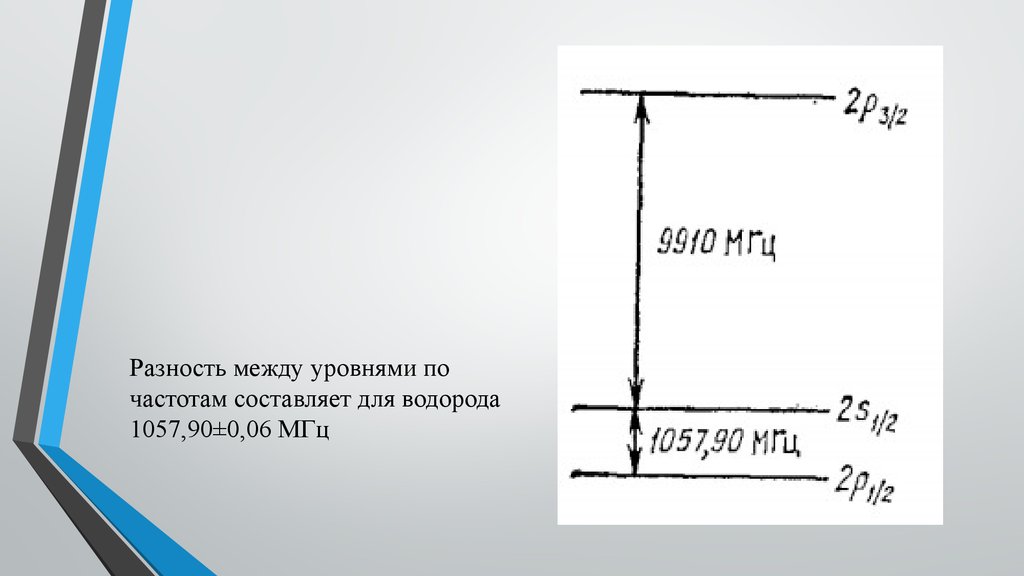
Разность между уровнями почастотам составляет для водорода
1057,90±0,06 МГц
7. Вывод формулы в рамках нерелятивистской квантовой теории
• энергия электрона в водородоподобном атоме
8.
(2)• – потенциал ионизации водорода
• n - главное квантовое число
•• k = j + 1/2, j - квантовое число полного орбитального момента
количества движения
• Z - заряд ядра
• α=
9. Hψ=ħ^2/(2µ) ∆ψ+Uψ=Eψ (3)
(3)• µ -механическая масса
• – волновая функция
10. W=-(2e^3)/(3πħc^3 m^3 ) ∫2_0^k▒〖kdk∑1_n▒|<0|p|n>|^2/(E_n-E_0+k)〗 (4)
• <0 |р | n> - матричный элемент оператора импульса•
и - энергии в начальном и «промежуточном» состояниях
11. W_своб=-(2e^2)/(3πħc^3 m^3 ) ∫2_0^k▒〖<0|p^2 |0>dk (5)〗 W_связ=-(2e^3)/(3πħc^3 m^3 )[∫2_0^k▒〖<0|p^2 |0> dk+〗 ∫2_0^k▒〖dk∑1_n▒〖|<0|p|n>|^2 (k/(E_n-E_0+k)-1)] (6)〗〗
•• Далее выбирая импульсы свободного и связанного электронаодинаковыми и составляя разность
12. W^′=(2e^3)/(3πħc^3 m^3 ) ∫2_0^k▒∑1_n▒〖|<0|p|n>|^2 ((E_n-E_0)/(E_n-E_0+k))dk (7)〗
Пусть k много больше всех возможных разностей энергий13.
•• Заменим ln|| средним14.
(10)(11)
(12)
(13)
15.
- оператор Лапласса(15)
16.
Для смещения уровняводородоподобного атома получаем
(17) ;
17.
(18)(19)
18. W^′=8/3π(e^2/ħс )^3 R Z^4/n^3 ln (mc^3)/(∆E)_ср
• Для численной оценки вклада будем использовать значенияфизических констант определенных для гелия:
Z=2, n=2, , (R=13.5 эВ), ħ=6.582·10-16 эВ·с, π=3.14, е=1.6·10-19 Кл,
с=3·108 м/с2
19. Заключение
Таким образом мы вычислили лэмбовский сдвиг для гелия в рамках
нерелятивистской квантовой механики и полученный результат
удовлетворяет современные экспериментальным значениям.
Лэмбовский сдвиг представляет большой интерес в квантовой
физике, с его помощью обнаружили ошибочность уравнения Дирака.
Мы видим, что уже в нерелятивистской квантовой механике можно
развить теорию, которая даёт результат, достаточно хорошо
совпадающий с опытом, несмотря на то, что по существу задача
является релятивистской.
20. Библиографический список
1. Я. А. Смородинский, Журнал “Успехи физических наук” 1949г.2. У. Паркер, Б. Тэйлор, Д. Лангенберг, Журнал “Успехи физических наук” 1968г.
3. С. Дрелл, Журнал “Успехи физических наук” 1980г.
4. С. Бродский, С. Дрелл, Журнал “Успехи физических наук” 1972г.
5. Peter W. Milonni, The quantum vacuum, Academic press inc. 1994г.
6. Д.В. Сивухин, Атомная и ядерная физика, т.5, издательство “Физико7.
математическая литература” 2006.
Е.Е Салпетер, Журнал “Успехи физических наук” 1953г.





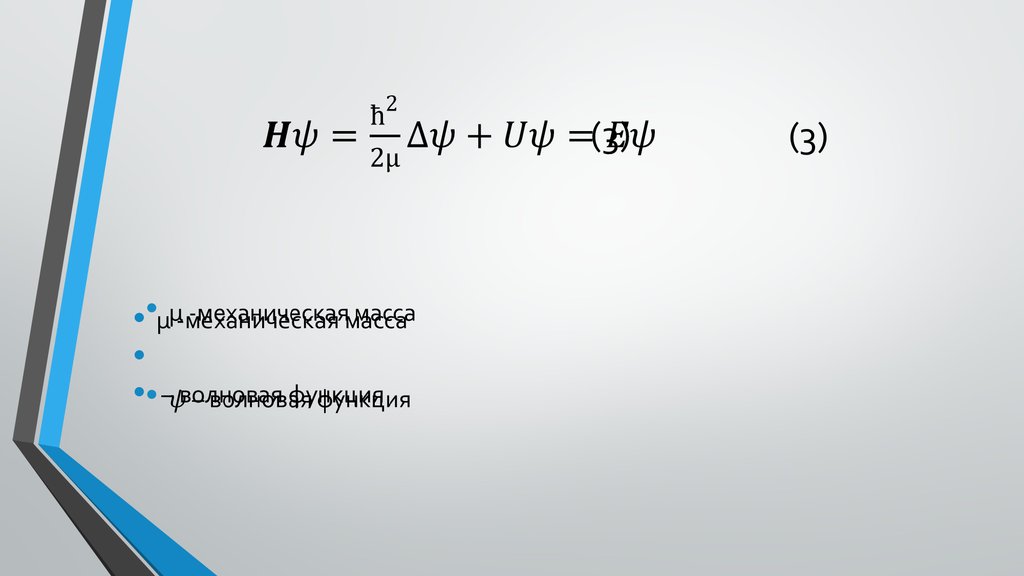

![W_своб=-(2e^2)/(3πħc^3 m^3 ) ∫2_0^k▒〖<0|p^2 |0>dk (5)〗 W_связ=-(2e^3)/(3πħc^3 m^3 )[∫2_0^k▒〖<0|p^2 |0> dk+〗 ∫2_0^k▒〖dk∑1_n▒〖|<0|p|n>|^2 (k/(E_n-E_0+k)-1)] (6)〗〗 W_своб=-(2e^2)/(3πħc^3 m^3 ) ∫2_0^k▒〖<0|p^2 |0>dk (5)〗 W_связ=-(2e^3)/(3πħc^3 m^3 )[∫2_0^k▒〖<0|p^2 |0> dk+〗 ∫2_0^k▒〖dk∑1_n▒〖|<0|p|n>|^2 (k/(E_n-E_0+k)-1)] (6)〗〗](https://cf.ppt-online.org/files/slide/u/Uarc6Ln2wupky5sVAOzEjSFKeXWYlT4gM9DbQB/slide-10.jpg)

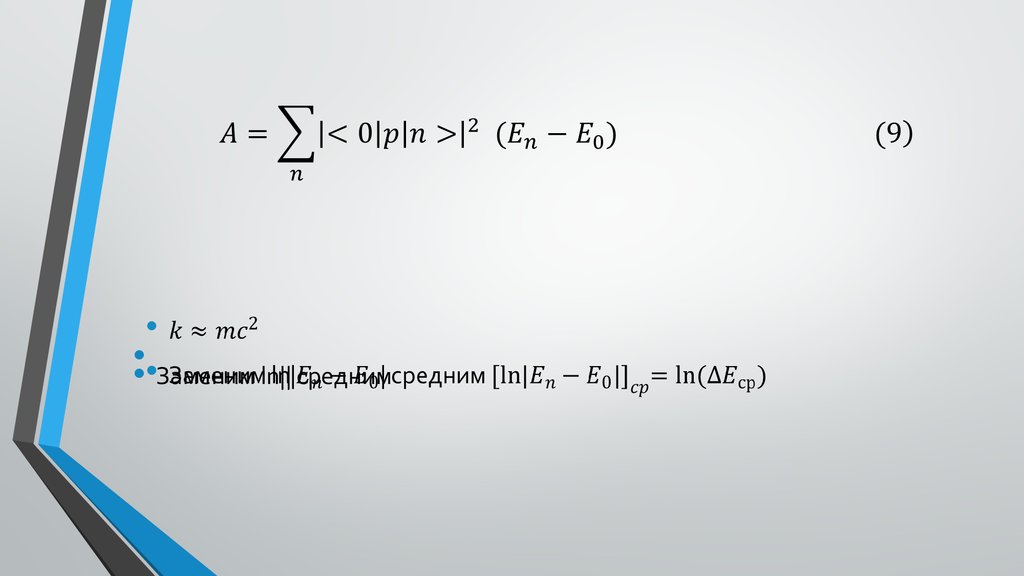
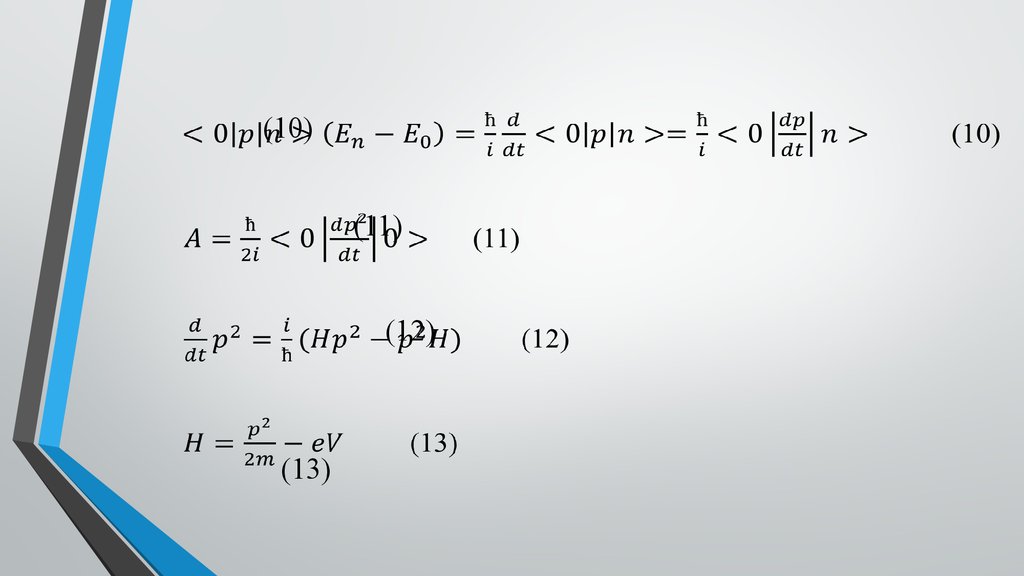
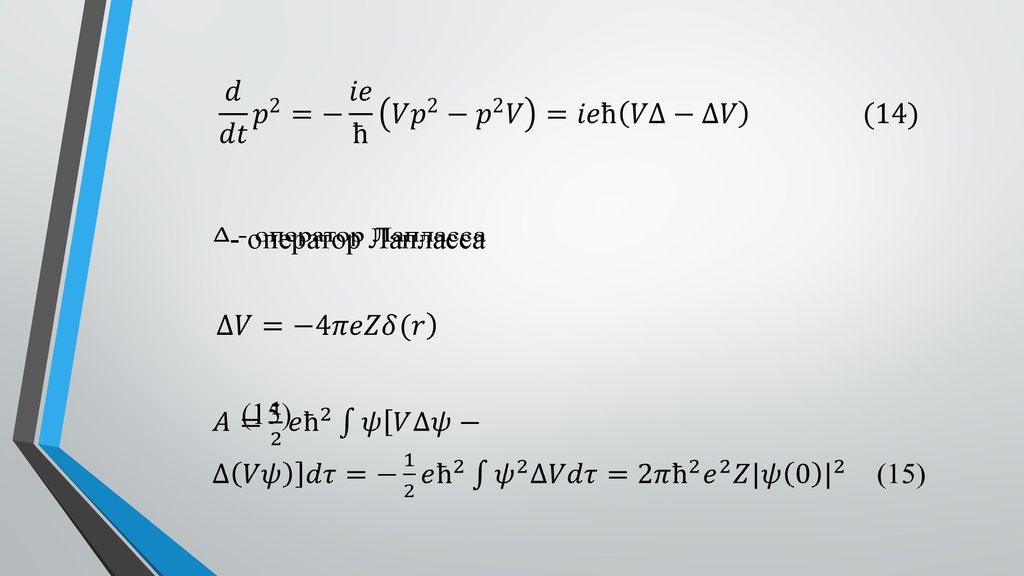

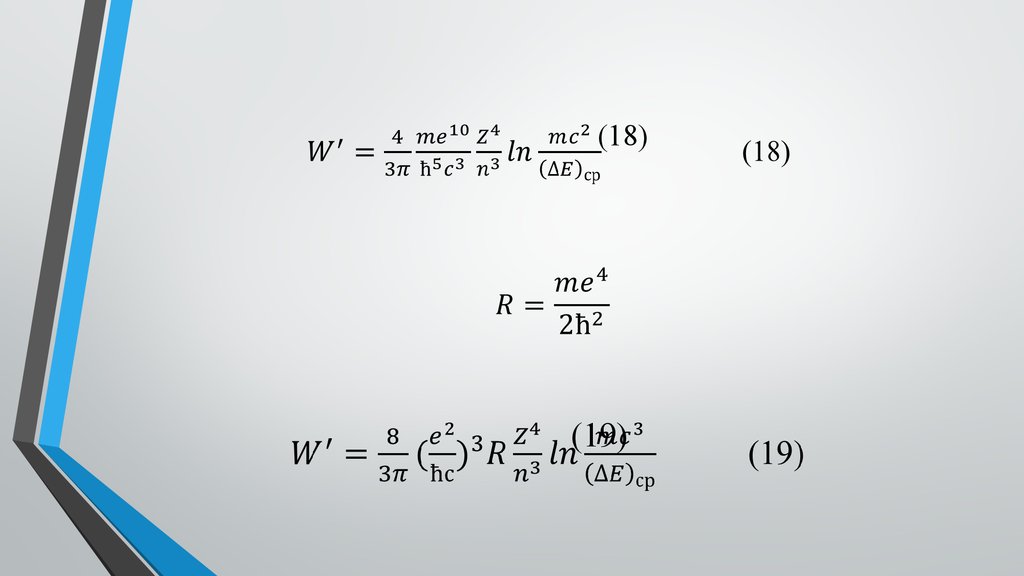




 Физика
Физика








