Похожие презентации:
Атом и центральное поле
1. Атом и центральное поле
Государственное бюджетное образовательное учреждениевысшего профессионального образования Московской области
«Международный университет природы, общества и человека «Дубна»
(Университет «Дубна»)
Факультет естественных и инженерных наук
Кафедра Ядерной физики
Специальный семинар по физике ядра и ядерным реакциям
В.В.Самарин
Атом и центральное поле
Вопросы 5, 6, 7.
2016
1
2. Вопрос 5. Атом водорода.
• Движение в центральном поле.• Атом водорода: волновые функции и
уровни энергии
2
3. Движение в центральном поле
2m2
E U (r ) 0
Собственные значения операторов квадрата и проекции момента импульса,
квадрата орбитального момента и проекции орбитального момента
2
ˆ
M Ylm
Lˆ Ylm
2 2
2
l (l 1)Ylm ; Mˆ zYlm Lˆz mlYlm
3
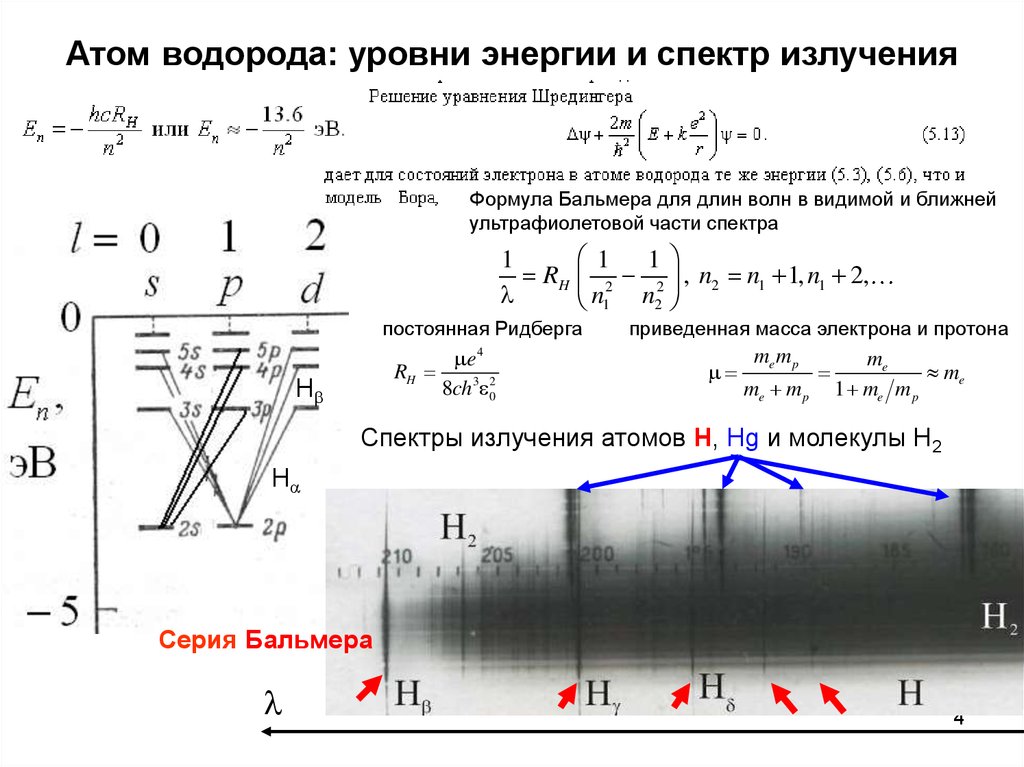
4. Атом водорода: уровни энергии и спектр излучения
Формула Бальмера для длин волн в видимой и ближнейультрафиолетовой части спектра
1
1
1
RH 2 2 , n2 n1 1, n1 2,
n1 n2
постоянная Ридберга
RH
Hb
e
8ch3 02
4
приведенная масса электрона и протона
me m p
me m p
me
me
1 me m p
Спектры излучения атомов H, Hg и молекулы Н2
Ha
Серия Бальмера
4
5. Атом водорода: спектральные серии, уровни энергии и волновые функции
21 e2
E ( n) 2
; aÁ
n 2aÁ
me 2
5
6. Сферические гармоники и полиномы Лежандра: пример расчета в Maple
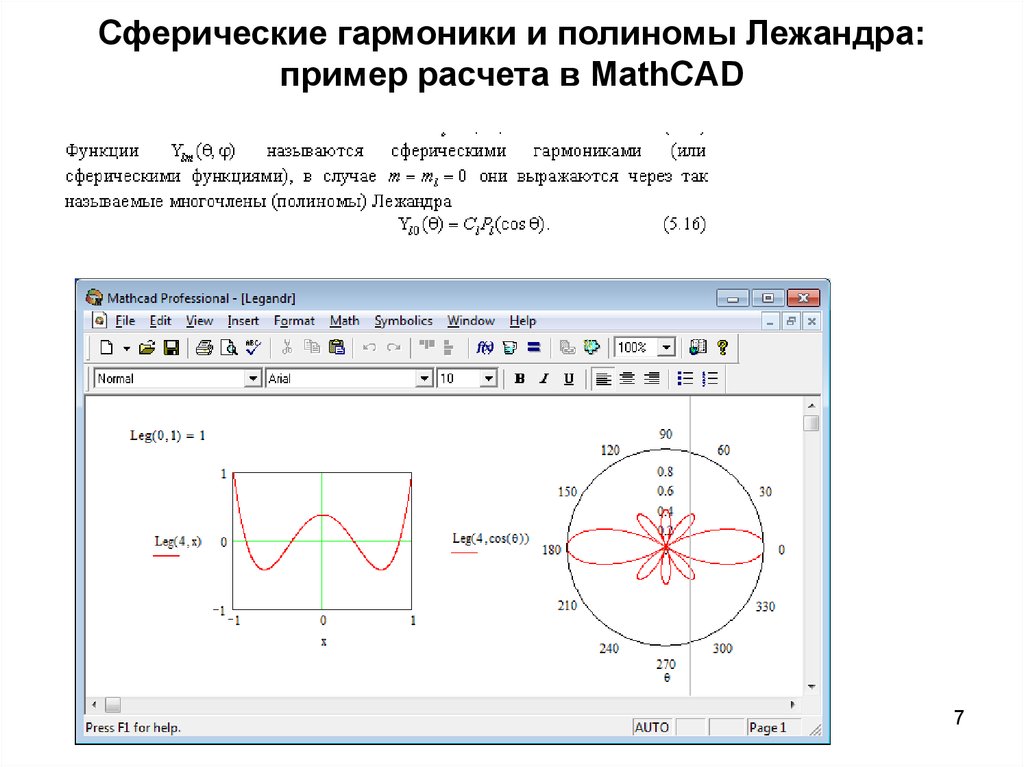
67. Сферические гармоники и полиномы Лежандра: пример расчета в MathCAD
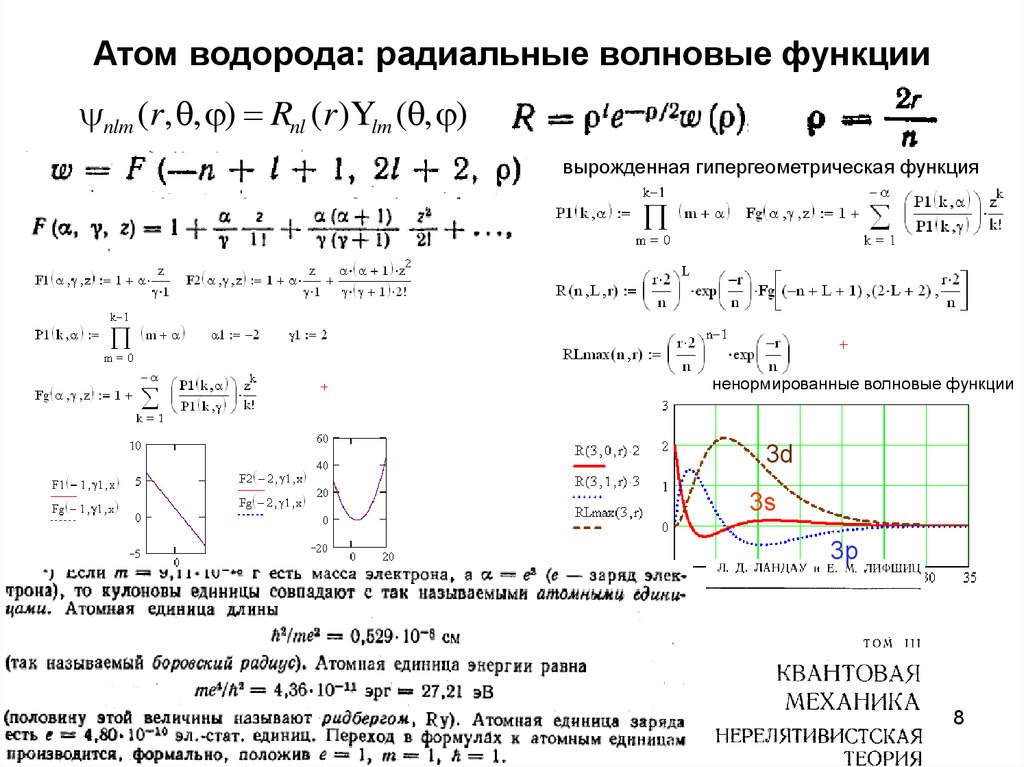
78. Атом водорода: радиальные волновые функции
nlm (r, , ) Rnl (r )Ylm ( , )вырожденная гипергеометрическая функция
ненормированные волновые функции
3d
3s
3p
8
9. Атом водорода: радиальные волновые функции
nlm (r, , ) Rnl (r )Ylm ( , )вырожденная гипергеометрическая функция
3s
3d
3p
ненормированные волновые функции
3s
3d
3p
9
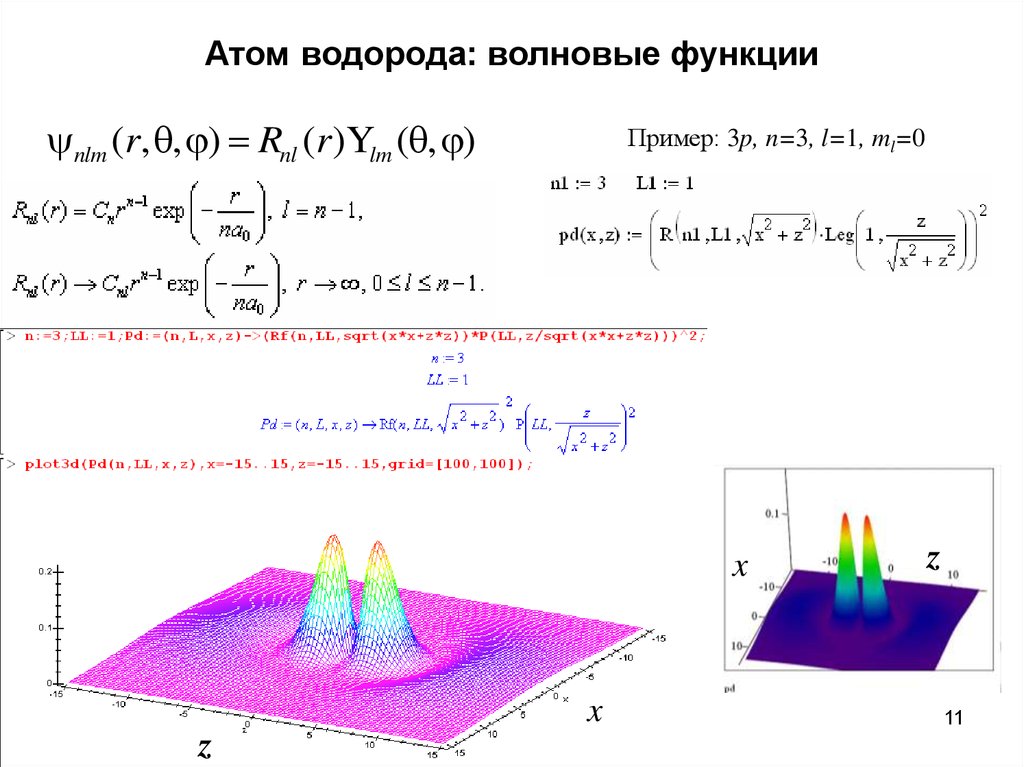
10. Атом водорода: волновые функции
nlm (r, , ) Rnl (r )Ylm ( , )Пример: 3p, n=3, l=1, ml=0
z
x
10
11. Атом водорода: волновые функции
nlm (r, , ) Rnl (r )Ylm ( , )Пример: 3p, n=3, l=1, ml=0
x
x
z
z
11
12. Вопрос 6. Атом в магнитном и электрическом поле: стационарная теория возмущений.
• Стационарная теория возмущений в отсутствиевырождения.
• Стационарная теория возмущений при наличии
вырождения.
• Эффект Зеемана
• Эффект Штарка
12
13. Стационарная теория возмущений в отсутствие вырождения
Hˆ Vˆ Ec V c ; V
Hˆ Hˆ 0 Vˆ ; Hˆ 0 (0) E (0) (0) ;
(0)
E
E
k
cm (0)
m ;
m
0
k
km m
km
Vˆ (0)
m dq
(0)*
k
m
ˆ (0) dq
E En(0) En(1) ; ck kn ck(1) ; äëÿ k n : En(1) Vnn (0)*
V
n
n
для k n : с
(1)
k
Vmn
Vkn
Vmn
(1)
(1)
(0)
(0)
;
с
0;
n
n
m
(0)
(0)
(0)
En Ek
m n En Ek
(0)
n
E
E
(0)
k
(2)
n
; E
m n
Vmn
(0)
n
E
2
E
(0)
k
(2)
0
; E
m n
Vmn
(0)
0
E
2
E
(0)
k
0
13
14. Стационарная теория возмущений при наличии вырождения
(0) (0)ˆ (0) E (0) (0) ,
Hˆ Hˆ 0 Vˆ ; Hˆ 0 (0)
E
;
H
n
n
n
0 n
n
n
cm (0)
m ;
m
(0)
(0)* ˆ (0)
E
E
c
V
c
;
V
k k km m km k V m dq
m
E En(0) En(1) ; cn cn(0) , cn cn(0)
,
En(1) cn Vnn cn(0)
;
n
; для En(0) En(0)
: ck 0, для Ek(0) En(0)
(1)
(0)
(1)
V
E
c
0;
V
E
nn n nn n
nn
n nn 0
n
секулярное уравнение
14
15. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета спина)
22
1
e
1
e
ˆ A U ; A 1 Hr
ˆ
H
p
A
e
;
H
p
2m
c
2m
c
2
2
e
Hˆ H 0
Aa pa
mc a
2mc 2
e
Hˆ Hˆ 0
A ;
2
a
Магнетон Бора
a
ˆ
H ra pˆ a Hˆ 0 B LH; B
2mc a
2mc
e
e
L
M L
cM (0)
M
Поправка к энергии состояния с орбитальным моментом L по формуле для наличия
вырождения по орбитальному магнитному квантовому числу M=-L,…L
* ˆ (0)
(0) * ˆ
(0)
(0) *
(0)
VM M (0)
V
dq
H
L
dq
H
M
LM
LM
B z
LM
z LM
B z
LM
LM dq
B H z M M M
VM M EM(1) M M 0 B H z M M M EM(1) M M 0
Поправка к энергии по формуле для отсутствия вырождения
E En(0) En(1) ; En(1) E B H Lz = B H M L ; M L L,
L 0 : En(1)
L
2
2
2
e2
e
e
2
2
215
0, E
A
H
r
H
r
;
a
a
a
2
2
2
2mc a
8mc a
12mc
a
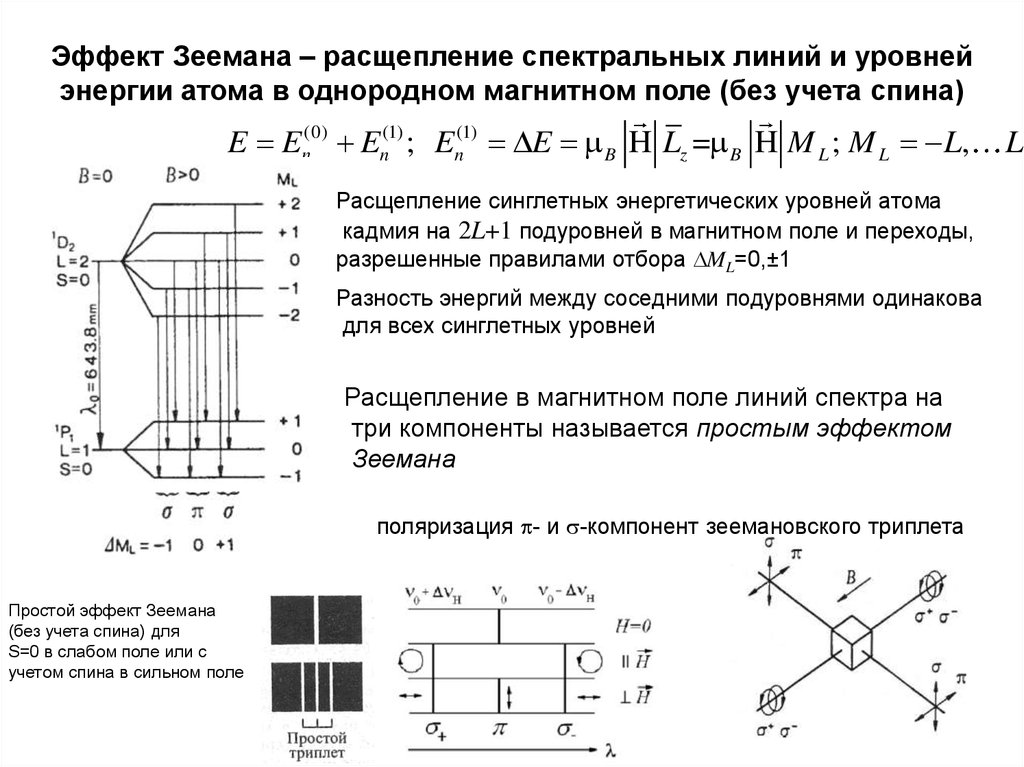
16. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета спина)
E En(0) En(1) ; En(1) E B H Lz = B H M L ; M L L,Расщепление синглетных энергетических уровней атома
кадмия на 2L+1 подуровней в магнитном поле и переходы,
разрешенные правилами отбора ML=0,±1
Разность энергий между соседними подуровнями одинакова
для всех синглетных уровней
Расщепление в магнитном поле линий спектра на
три компоненты называется простым эффектом
Зеемана
поляризация p- и s-компонент зеемановского триплета
Простой эффект Зеемана
(без учета спина) для
S=0 в слабом поле или с
учетом спина в сильном поле
16
L
17. Эффект Зеемана – расщепление красной спектральной линии атома кадмия в однородном магнитном поле (без учета спина)
Изображение интерференционной картинына экране компьютера с без магнитного поля.
Использован интерферометр Фабри-Перо.
Изображение интерференционной картины
на экране компьютера для простого
“поперечного” эффекта Зеемана
Наблюдения спектров излучения чаще всего производят по нормали к направлению магнитного поля
(“поперечный” эффект Зеемана) или по направлению поля (“продольный” эффект Зеемана).
При продольном эффекте Зеемана видны только смещенные s-компоненты зеемановского триплета,
которым соответствует циркулярно поляризованный свет. Двум направлениям круговой поляризации
(по и против часовой стрелки) соответствуют два возможных значения проекции момента импульса
фотона на направление движения и два значения проекции спина фотона. При наблюдении поперек поля
эти линии оказываются линейно поляризованными. Вектор напряженности электрического поля E
колеблется перпендикулярно направлению магнитного поля . Несмещенная p-компонента не видна при
наблюдении вдоль поля, а при наблюдении поперек поля линейно поляризована, причем вектор E 17
колеблется вдоль направления магнитного поля .
18. Эффект Штарка - расщепление спектральных линий и уровней энергии в однородном электрическом поле
V Ed E d z1. Атом водорода: линейный эффект Штарка
En(1) cn Vnn cn(0)
;
n
(1)
(0)
(1)
V
E
c
0;
V
E
nn n nn n
nn
n nn 0
n
2. Сложный атом: квадратичный эффект Штарка
ˆ (0) dq 0
E En(0) En(1) ; ck kn ck(1) ; k n : En(1) Vnn (0)*
V
n
n
Vmn
(0)
n
E
E
(0)
k
(2)
n
; E
m n
Vmn
(0)
n
E
2
E
(0)
k
(2)
0
; E
m n
Vmn
(0)
0
E
2
E
(0)
k
0
Эффект Штарка:
1. Линейный у атома водорода и водородоподобных атомов (в слабых полях), связан с
вырождением уровней энергии по орбитальному квантовому числу в кулоновском поле.
Средний дипольный момент таких атомов не равен нулю. Энергия подуровней зависит от
главного квантового числа, орбитального квантового числа и модуля магнитного
орбитального квантового числа. Например состояние с n =2 расщепляется на 3 подуровня, в
общем случае на 2n -1 подуровень.
2. Квадратичный у атома водорода и водородоподобных атомов в сильных полях, у
многоэлектронных атомов с нулевым средним дипольным моментом.
18
19. Литература
1. Сивухин, Д. В. Общий курс физики. В 5Т. Т 5: Атомная и ядерная физика:
учеб. пособие– М.: Физматлит, 2002
2. Ландау Л.Д. Лифшиц Е.М. Краткий
курс теоретической физики. Т. 2.
Квантовая механика. − М. Наука. 1971.
19
20. Вопрос 7. Релятивистские эффекты в водородоподобном атоме.
Уравнение Дирака.
Квазирелятивистское приближение.
Спин-орбитальное взаимодействие.
Тонкая структура спектра атома
водорода.
20
21. Уравнение Дирака
Свободное движениеi
Матрицы Паули
capˆ mc 2b ; ; 1 ; 3 ;
t
2
4
0 s
I 0
0 1
0 i
1 0
a
; b
; s1
; s2
; s3
;
s 0
0 I
1 0
i 0
0 1
Состояния с определенным значением импульса p и энергии
mc 2 csp 0 mc 2
csp
;
0; c p 2 m2 c 2
2
2
csp mc
csp mc 0
положительные и
отрицательные “частоты”
e
Движение в электромагнитном поле pˆ pˆ A; eA0
c
ˆ e
2
cspˆ mc 2
2
ˆ
c
s
p
mc
В центральном поле
Операторы проекций внутреннего
углового момента (спинового момента)
sˆ
2
s
Оператор спина
для электрона е<0
cs p c A eA0 mc
cs pˆ e A eA mc 2
0
c
ˆj lˆ sˆ
1
sˆ s sˆ1 , sˆ2 , sˆ3
2
Для атома водорода
cspˆ mc 2 e2 r
2
2
cspˆ mc e r
Шаровые спиноры – собственные функции
ˆj 2 , lˆ2 , ˆjz2
l m 1 2
l m 1 2
Y
l , m 1 2
f
(
r
)
Y
j ,l , m
l , m 1 2
2l 1
l j 1 2;
2
l
1
1 l l
;
l 1 2, l , m
l m 1 2
l 1 2,l , m
l
2
j
l
;
2
j m 1 2
( 1)
g ( r ) j , l , m
Yl , m 1 2
Yl , m 1 2
2l 1
2l 1
1
f mc 2 1e 2 Q Q
1
2
1
1
2
2
j 1 2 (l 1), j l 1 2;
f
f
mc
e
r
g
0
2
1 2
r
c
g mc e Q1 Q2 0
j 1 2 l , j l 1 2;
1
1
g
g mc 2 e 2 r f 0 2 r ; ( ) m 2 c 2 2 c 2 ; 2 a 2
0,1, 2, , 0, j l 1 2;
r
c
nr
a
1, 2,3, , 0, j l 1 2;
nr
; целое положительное число
21
c ( )
Берестецкий В.Б. Лифшиц Е.М., Питаевский Л.П. Квантовая электродинамика
22. Решения уравнения Дирака для атома водорода: уровни энергии
j 1 2 (l 1), j l 1 2;j 1 2 l , j l 1 2;
0,1, 2,
nr
1, 2,3,
, 0, j l 1 2;
, 0, j l 1 2;
e2
1
a
4p 0 c 137
СИ
e2
1
a
c 137
Гауссова система единиц
точное выражение
mc 2
1
n
r
mc 2 E (nr , j )
a2
a
2
2
2
приближенное выражение
2
1 e2 a 2 1
3
E (n, j ) 2
; aB 2
1
n 2aÁ
n j 1 2 4n
me
22
23. Решение уравнения Дирака для атома водорода: энергии
j 1 2 (l 1), j l 1 2;j 1 2 l , j l 1 2;
1
E (nr , j ) mc 2 mc 2 (
1
точное
выражение
a
nr a
1
n
r
a
2
2
a 2 (2 )
2
1
a
n
r
2
2
1 2 a
2
(2 ( nr )
a
1)
2
nr 1 a
2
2
1
1) mc 2 (
1
mc 2 (
1
2
e2
1
a
c 137
1
1) mc 2 (
2
2
1
mc 2 (
, 0, j l 1 2;
e2
1
a
, 0, j l 1 2;
4p 0 c 137
0,1, 2,
nr
1, 2,3,
1
a
n
r
2
приближенные
выражения
1)
2
1 a 2 (2 (nr )
2
2
1)
2
2
2
a
1 2
a
2
2
2
mc
1
2
a
(2
(
n
)
1
2
a
(2
(
n
)
r
r
2 n 2
3 4 nr 2
r
1
mc 2 a 2
a2
3
1
me 4
2 2
1
; nr n; j ; mc a 2
2
2
4 nr
2 nr nr
2
1 e2 a 2 1
3
E (n, j ) 2
; aB 2
1
n 2aB
n j 1 2 4n
me
приближенное выражение
23
24. Решение уравнения Дирака для водородоподобного атома : энергия основного состояния
2cspˆ mc 2 Z e2 r
2
2
cspˆ mc Z e r
Ze 2
Z
Za
4p 0 c 137
СИ
Гауссова система
единиц
e2
1
a
c 137
n0 0, 0 1
mc
0
1
Z a
2
n
0
2
Z a
2
0
2
2
2
1
mc 2 E (nr 0, j ) mc 2 1 1
2
0
mc 2
Чисто кулоново поле можно рассматривать в теории Дирака
лишь при Za<1, т.е. Z<137.
Zmax=137
24
25.
Решение уравнения Дирака для водородоподобного атома с ядромконечного размера: энергия основного состояния
25
26. Квазирелятивистское приближение.
22
Нерелятивистское движение в слабом электромагнитном поле E mc ; E eA0 mc
e
2
cs p c A eA0 mc
cs p e A eA mc 2
0
c
2
e
e
1
sH
p A eA0
2
m
c
2
mc
Для электрона е<0
E ; H rotA;
Уравнение Паули
e
e
e
e
sH H 2 0 s H; 0
;
s
s 2 0 s
2mc
2mc
2mc
2mc
Магнетон Бора
Движение в слабом центральном электростатическом поле eA0=V(r)
с точностью до членов порядка v2/c2
E g E ( gH g 1 ) g H
1 2
p V (r ) W1 W2 W3 E
2m
W1
2
8m2 c 2
V
E V
2
W2
W3
2mc 2
2 2
4m c
Оператор
контактного
взаимодействия
pˆ 2
g 1
4m 2 c 2
В кулоновском поле V(r)= e2Z/r
12
pˆ 2
1
2 2
8m c
W1
2
2 2
8m c
V
2
2 2
8m c
4pZe 2 (r )
Поправка к оператору кинетической энергии,
из-за изменения массы частицы при
изменении ее скорости
s V p
1 V ˆ ˆ
sL
2 2
r
r
2m c
Оператор спин-орбитального взаимодействия
26
27. Спин-орбитальное взаимодействие.
Спин-орбитальное взаимодействие.
резкая серия
главная серия
Схема образования дублетных линий
главной и резкой серий натрия
27
28. Спин-орбитальное взаимодействие.
Спин-орбитальное взаимодействие.
резкая серия
главная серия
Водород E=4*10-5 эВ
28
Схема образования дублетных линий
главной и резкой серий натрия
29. Тонкая структура спектра атома водорода.
21 e2 a 2 1
3
E (n, j ) 2
; aB 2
1
n 2aB
n j 1 2 4n
me
Лэмбовский сдвиг уровней
Сверхтонкая структура
E=4*10-5 эВ
29
























 Физика
Физика








