Угловой момент, центральное поле, атомы водорода и гелия

1. Угловой момент, центральное поле, атомы водорода и гелия

Государственный университет «Дубна»
Инженерно-физический институт
Кафедра ядерной физики
Кафедра фундаментальных проблем физики микромира
Специальный семинар по физике ядра и ядерным реакциям
В.В.Самарин
Угловой момент, центральное поле,
атомы водорода и гелия
Вопросы 7, 8, 9, 10, 11.
2019
1

2.

Вопрос 7
• Угловой момент
• Движение в центральном поле.
• Атом водорода: волновые функции и
уровни энергии
2

3. Угловой момент

Оператор момента импульса
e
x
ˆ ˆ
M r p det x
i
x
ey
y
i
y
ez
z
i
z
ex i y i z e y i x i z ez i x i y
z
y
z
x
y
x
ex Mˆ x e y Mˆ y ez Mˆ z ex Lˆx e y Lˆ y ez Lˆz
1 2
1
ˆ
ˆ2
2
2
2 ˆ2
2
2
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
M M x M y M z , L Lx Ly Lz , 2
sin , Lz i
2
sin sin
2
2
2
1 2 1
2 2 2 2
r
,
x y
z
r r r r 2
Собственные значения операторов квадрата и проекции момента импульса,
квадрата орбитального момента и проекции орбитального момента
Mˆ 2Ylm
Lˆ Ylm
2 2
2
l (l 1)Ylm ; Mˆ zYlm Lˆz mlYlm
l=0,1,2,…; ml=0,±1, ±2,…±l
3

4. Сферические гармоники и полиномы Лежандра: пример расчета в Maple

4

5. Сферические гармоники и присоединенные функции Лежандра

Pl
( m)
( x) 1 x
2
m
2
dm
P ( x)
m l
dx
5

6. Сферические гармоники и гипергеометрическая функция

6

7. Сферические гармоники: пример расчета в Maple

7

8. Движение в центральном поле

2m
2
E U (r ) 0
для атома Н
8

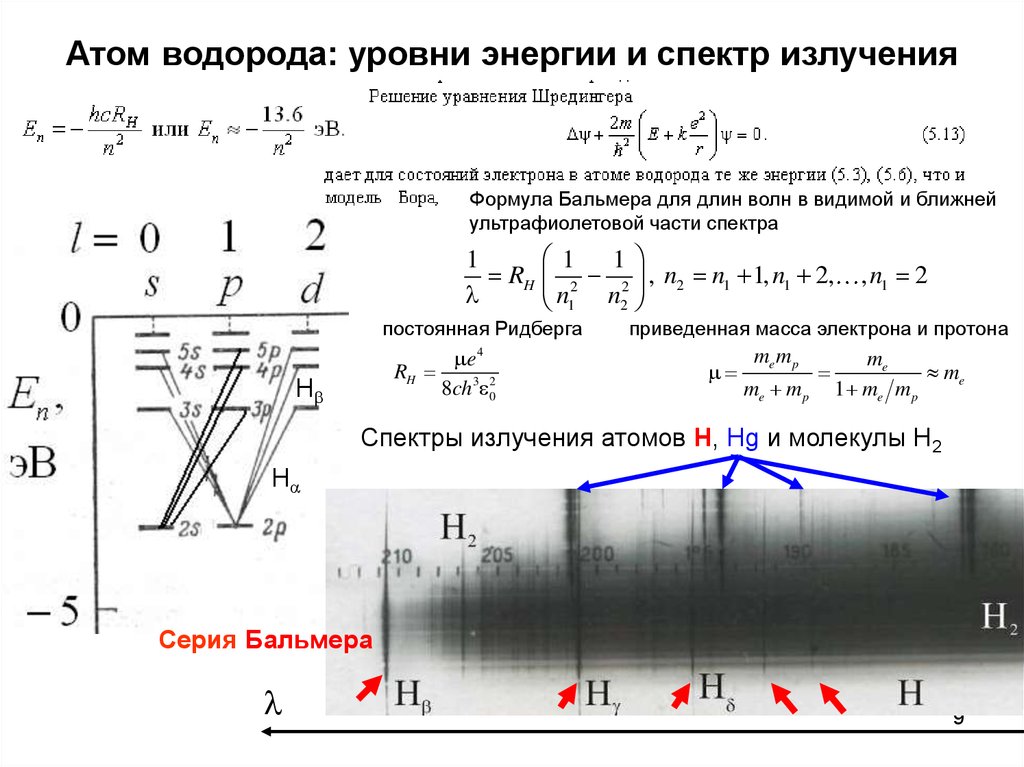
9. Атом водорода: уровни энергии и спектр излучения

Формула Бальмера для длин волн в видимой и ближней
ультрафиолетовой части спектра
1
1
1
RH 2 2 , n2 n1 1, n1 2,
n1 n2
постоянная Ридберга
RH
Hb
e
8ch3 02
4
, n1 2
приведенная масса электрона и протона
me m p
me m p
me
me
1 me m p
Спектры излучения атомов H, Hg и молекулы Н2
Ha
Серия Бальмера
9

10. Атом водорода: спектральные серии, уровни энергии и волновые функции

Атом водорода: спектральные серии, уровни энергии и волновые
2
функции
1 e2
E ( n)
n 2 2aÁ
; aÁ
me 2
, n 1, 2,
n главное квантовое число
l орбитальное квантовое число
l 0,1, 2,
n 1
Правила отбора при
испускании и
поглощении света
l = ± 1
10

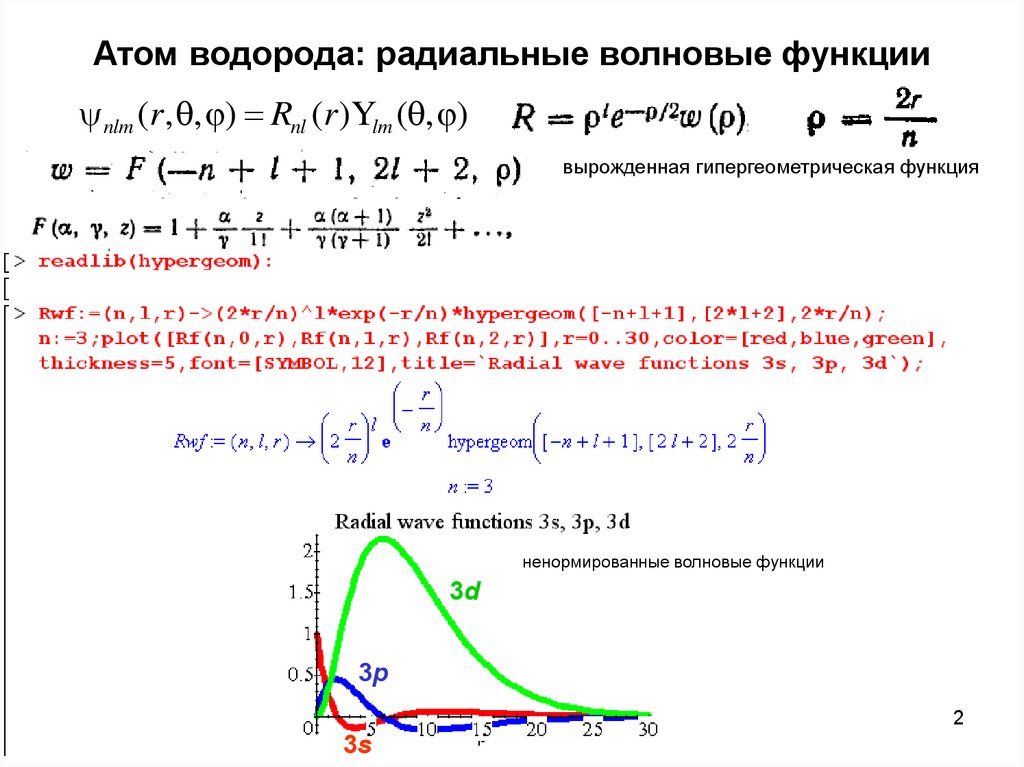
11. Атом водорода: радиальные волновые функции

nlm (r, , ) Rnl (r )Ylm ( , )
вырожденная гипергеометрическая функция
ненормированная волновая функция
11

12. Атом водорода: радиальные волновые функции

nlm (r, , ) Rnl (r )Ylm ( , )
вырожденная гипергеометрическая функция
ненормированные волновые функции
3d
3p
12
3s

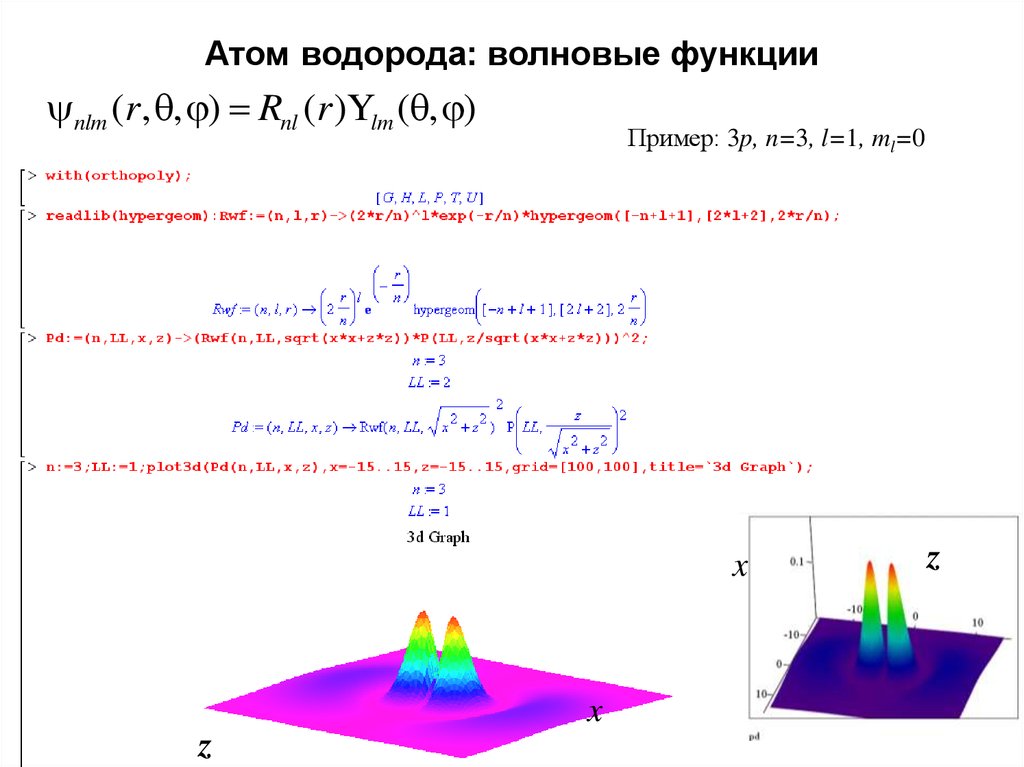
13. Атом водорода: волновые функции

nlm (r, , ) Rnl (r )Ylm ( , )
Пример: 3p, n=3, l=1, ml=0
x
x
z
z
13

14. Вопрос 8.

1. Теория упругого рассеяния:
дифференциальное сечение рассеяния,
волновая функция и амплитуда
рассеяния
2. Борновское приближение.
3. Парциальное разложение амплитуды
рассеяния.
4. Оптическая модель.
14

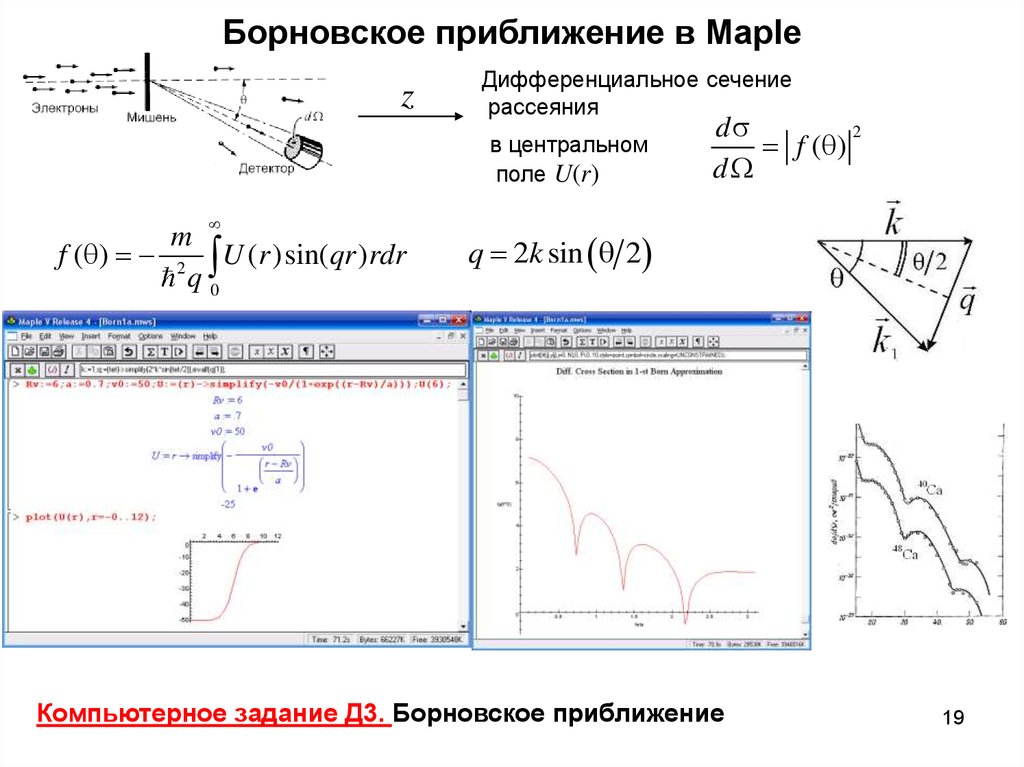
15. Дифференциальное сечение рассеяния

Типичный эксперимент по рассеянию частиц:
упругое рассеяние быстрых электронов на атомных ядрах
I( )
ds 1
1
I ( ), d s I ( )d W
dW j
j
Рис. 1.
Рис. 2.
Зависимости от угла дифференциальных сечений рассеяния
электронов с энергией 750 МэВ на ядрах кальция. Значения
сечений рассеяния на ядрах 40Ca увеличены в 10 раз,
а на ядрах 48Ca уменьшены в 10 раз.
Основным источником сведений о распределении электрического заряда в атомном ядре
явилось исследование рассеяния быстрых электронов на ядрах, начатое Р. Хофштадтером
с 1956 г. (Нобелевская премия по физике за 1961 г.). Схема опыта была аналогична схеме
опыта Резерфорда с заменой альфа-частиц от радиоактивного препарата на ускоренные
электроны. В типичных экспериментах (см. рис. 1) интенсивный пучок релятивистских
электронов с энергией от 150 МэВ до нескольких ГэВ направлялся из ускорителя в камеру с
мишенью в виде тонкой плёнки. Измерялась интенсивность I( ) [1/c] потока электронов,
рассеянных в элемент телесного угла dW [ ]. Отношение величины I( ) /dW [1/(ср с)] к плотности
потока налетающих частиц j [1/(см2 с)] представляет собой дифференциальное сечение
рассеяния ds/dW . Его значения принято записывать в см2/ср., фм2/ср. (1 фм = 10-15 м), б/ср.
(1 бн = 1 барн = 10-24 см2).
15

16. Волновая функция y и амплитуда рассеяния f(q)

Волновая функция и амплитуда рассеяния f( )
U(r) – центральное короткодействующее поле
z
Плоская волна
1
(r ) f ( ) exp(ikr ), r
r
1
Et
(r , t ) f ( ) exp i kr
r
( z ) exp(ikz )
Плотность потока вдоль оси z
i *
*
jz
2m z
z
i
2i Im exp(ikz ) exp( ikz )
2m
z
k
v
m
Отношение I( ) к плотности потока
налетающих частиц представляет
собой дифференциальное сечение
рассеяния ds/dW,
выражается в единицах бн/ср,
1 барн равен: 1 бн = 10-24 см2.
расходящаяся
сферическая волна
Волновая функция на больших расстояниях
к формуле 9
1
exp(ikz ) f ( ) exp(ikr ), r
r
Поток вероятности I( ) через dS=r2dW
I ( ) jr dS
i *
*
dS
2m r
r Детектор
i 1
2
2
2
i
Im
exp(
ikr
)
exp(
ikr
)
r
f
(
)
dW
2
2m r
r
k
2
2
f ( ) d W v f ( ) d W
m
d s 1 I ( )
1
2
2
f ( ) , d s I ( ) f ( ) d W
d W jz d W
jz
16
к формуле 9

17. Борновское приближение

Волновая функция
U(r) – центральное
Борновское приближение
z
(0) exp(ikz )
для свободного движения
короткодействующее поле
1
exp(ikz ) f ( ) exp(ikr )
r
(0) k 2 (0) 0,
для точного уравнения Шредингера
k 2
2m
2
m
f ( ) 2 U (r )sin(qr )rdr
q0
U 0
приближение для волновой функции:
q 2k sin 2
(0) (1) , (1) (0) .
Для приближенного уравнения
k
(1)
2
(1)
2m
2
U (0)
приближенное решение
на больших расстояниях:
формулы 10
Дифференциальное сечение
рассеяния
расходящаяся
сферическая
волна
1 exp(ikr ) 2m
(1)
U (r ) exp( iqr )dV
2
4
r
1
(1) f ( ) exp(ikr )
r
m
f ( )
U (r ) exp( iqr )dV
2
2
ds
2
f ( )
dW
Условия применимости
при больших скоростях
U
2
ma 2
ka
формулы 10
v
, ka 1
a
при малых скоростях
U
2
ma
2
, ka 1
17

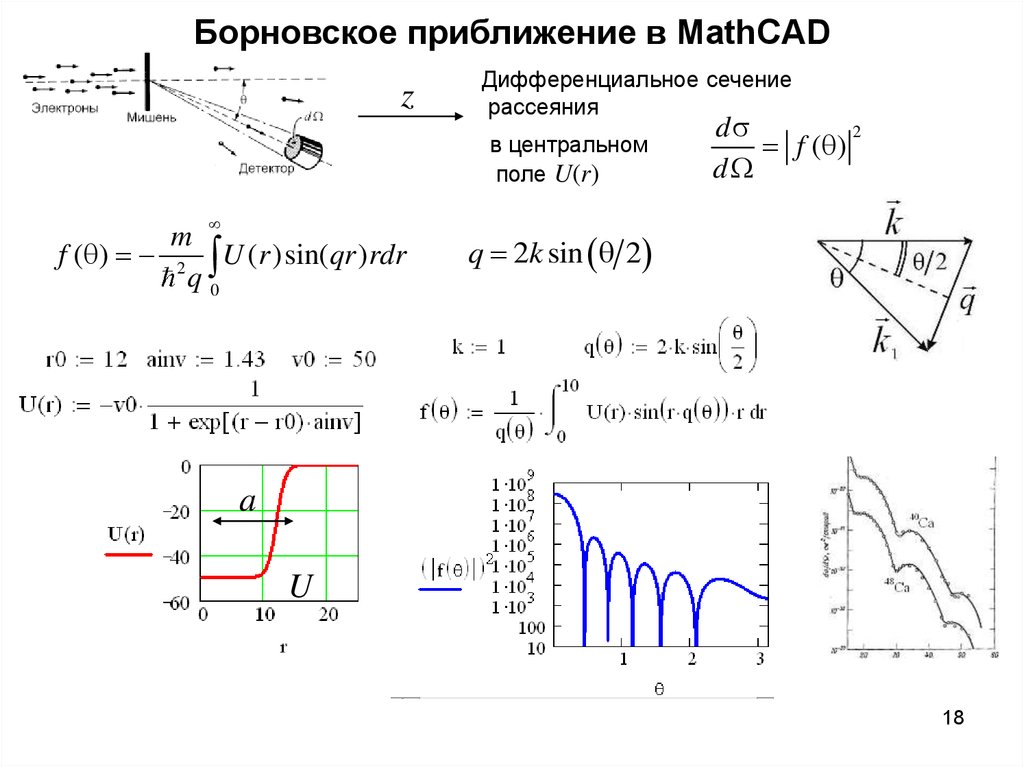
18. Борновское приближение в MathCAD

z
Дифференциальное сечение
рассеяния
в центральном
поле U(r)
m
f ( ) 2 U (r )sin(qr )rdr
q0
ds
2
f ( )
dW
q 2k sin 2
a
U
18

19. Борновское приближение в Maple

z
Дифференциальное сечение
рассеяния
в центральном
поле U(r)
m
f ( ) 2 U (r )sin(qr )rdr
q0
ds
2
f ( )
dW
q 2k sin 2
Компьютерное задание Д3. Борновское приближение
19

20. Борновское приближение в Maple

z
m
f ( ) 2 U (r )sin(qr )rdr
q0
Дифференциальное сечение
рассеяния
в центральном
поле U(r)
ds
2
f ( )
dW
q 2k sin 2
Компьютерное задание Д3.
Борновское приближение
20

21. Парциальное разложение амплитуды рассеяния: волновая функция частицы в центральном поле

Стационарное уравнение
Шредингера
2
2m
E U (r ) 0
2
Hˆ E ,
U (r ) E ,
2m
21

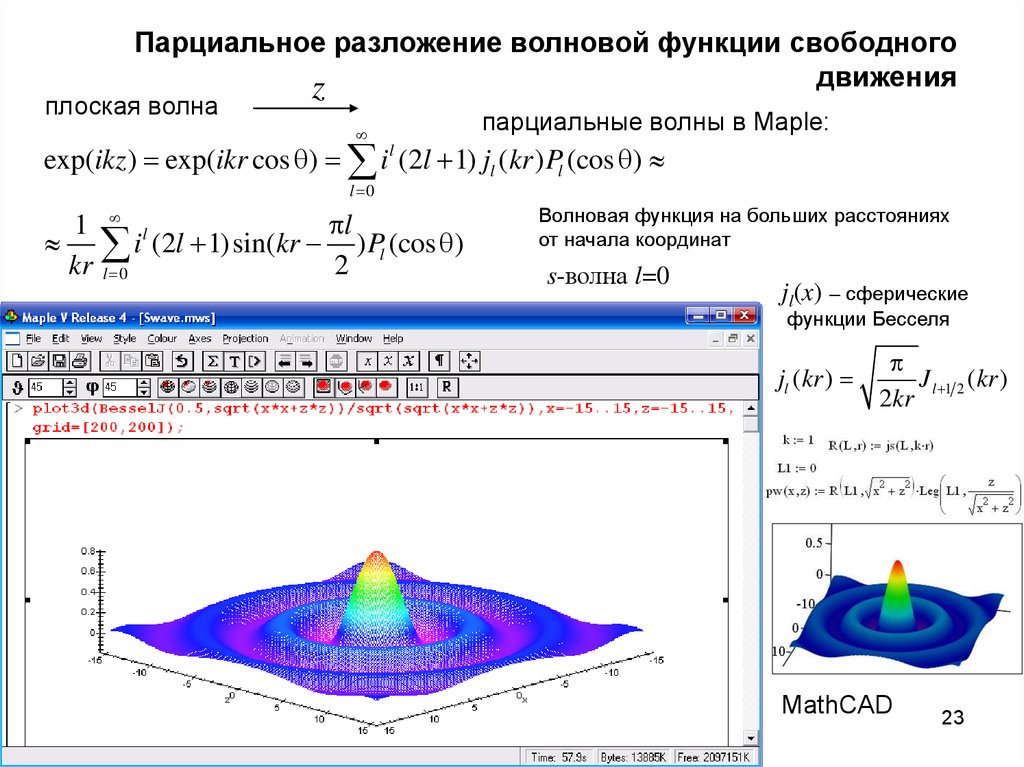
22. Парциальное разложение волновой функции свободного движения

плоская волна
z
jl(x) – сферические функции Бесселя
exp(ikz ) exp(ikr cos ) i l (2l 1) jl (kr ) Pl (cos )
l 0
1 l
l
i (2l 1) sin(kr ) Pl (cos )
kr l 0
2
Волновая функция на больших расстояниях
от начала координат
парциальные волны в MathCAD:
p-волна l=1
d-волна l=2
s-волна l=0
22

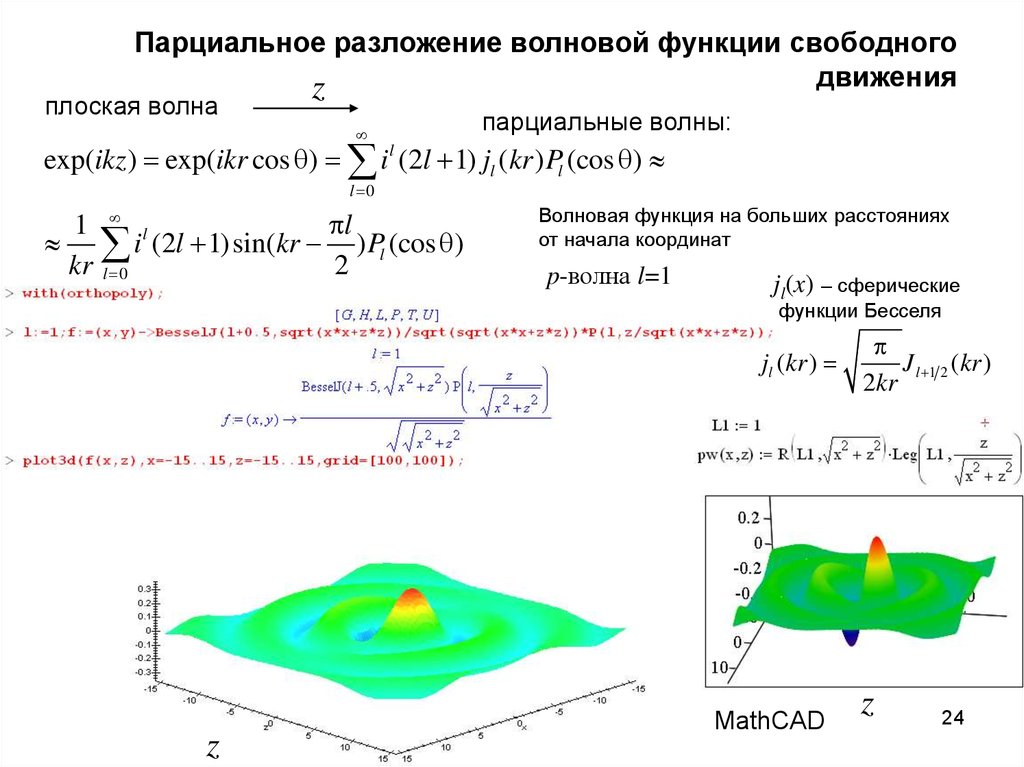
23. Парциальное разложение волновой функции свободного движения

z
плоская волна
парциальные волны в Maple:
exp(ikz ) exp(ikr cos ) i l (2l 1) jl (kr ) Pl (cos )
l 0
1 l
l
i (2l 1) sin(kr ) Pl (cos )
kr l 0
2
Волновая функция на больших расстояниях
от начала координат
s-волна l=0
jl(x) – сферические
функции Бесселя
jl (kr )
J l 1 2 (kr )
2kr
MathCAD
23

24. Парциальное разложение волновой функции свободного движения

z
плоская волна
парциальные волны:
exp(ikz ) exp(ikr cos ) i l (2l 1) jl (kr ) Pl (cos )
l 0
1 l
l
i (2l 1) sin(kr ) Pl (cos )
kr l 0
2
Волновая функция на больших расстояниях
от начала координат
p-волна l=1
jl(x) – сферические
функции Бесселя
jl (kr )
z
MathCAD
J l 1 2 (kr )
2kr
z
24

25. Парциальное разложение волновой функции свободного движения

z
плоская волна
парциальные волны:
exp(ikz ) exp(ikr cos ) i l (2l 1) jl (kr ) Pl (cos )
l 0
1 l
l
i (2l 1) sin(kr ) Pl (cos )
kr l 0
2
Волновая функция на больших расстояниях
от начала координат
d-волна l=2
jl(x) – сферические
функции Бесселя
jl (kr )
MathCAD
J l 1 2 (kr )
2kr
25

26. Парциальное разложение волновой функции и амплитуды рассеяния

Парциальное разложение волновой функции и
U(r) – центральное короткодействующее поле
амплитуды рассеяния
z Волновая функция
на больших расстояниях
от рассеивающего центра
Плоская волна
exp(ikz ) exp(ikr cos )
21
l
a
sin(
kr
) Pl (cos )
l
r l 0
2
1
l
l
i
(2
l
1)sin(
kr
) Pl (cos )
kr l 0
2
1
exp(ikz ) f ( ) exp(ikr )
r
Al (2l 1) Rkl ( r ) Pl (cos )
радиальная часть
парциальной волны
при свободном движении
Амплитуда рассеяния
дифференциальное
сечение рассеяния
l 0
1
l
A
(2
l
1)sin(
kr
l ) Pl (cos )
l
2 kr l 0
2
радиальная часть парциальной волны при рассеянии
1
(2l 1) ( 1)l exp( ikr ) exp(2i l ikr ) Pl (cos )
2kr l 0
сходящаяся сферическая волна расходящаяся сферическая волна
i
f ( )
(2l 1) [1 exp(2i l ) ] Pl (cos )
2k l 0 Диагональный элемент матрицы рассеяния S exp 2i
L
L
ds
2
dW
f ( )
полное сечение рассеяния равно
сумме парциальных сечений
l –парциальные фазы рассеяния
4
s 2 f ( ) sin d 2 (2l 1) sin 2 l
k l 0
0
2
формулы 11
26

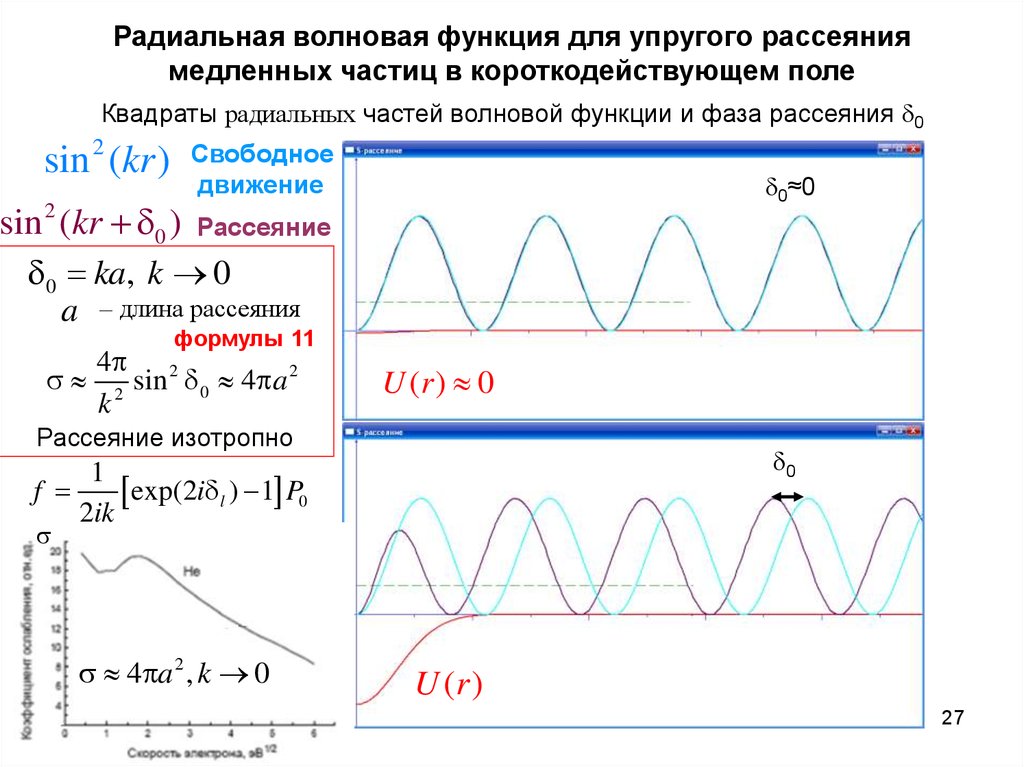
27. Радиальная волновая функция для упругого рассеяния медленных частиц в короткодействующем поле

Квадраты радиальных частей волновой функции и фаза рассеяния 0
sin 2 (kr )
sin 2 (kr 0 )
Свободное
движение
0≈0
Рассеяние
0 ka, k 0
a – длина рассеяния
формулы 11
s
4 2
2
sin
4
a
0
k2
U (r ) 0
Рассеяние изотропно
0
1
f
[exp(2i l ) 1] P0
2ik
s
s 4 a 2 , k 0
U (r )
27

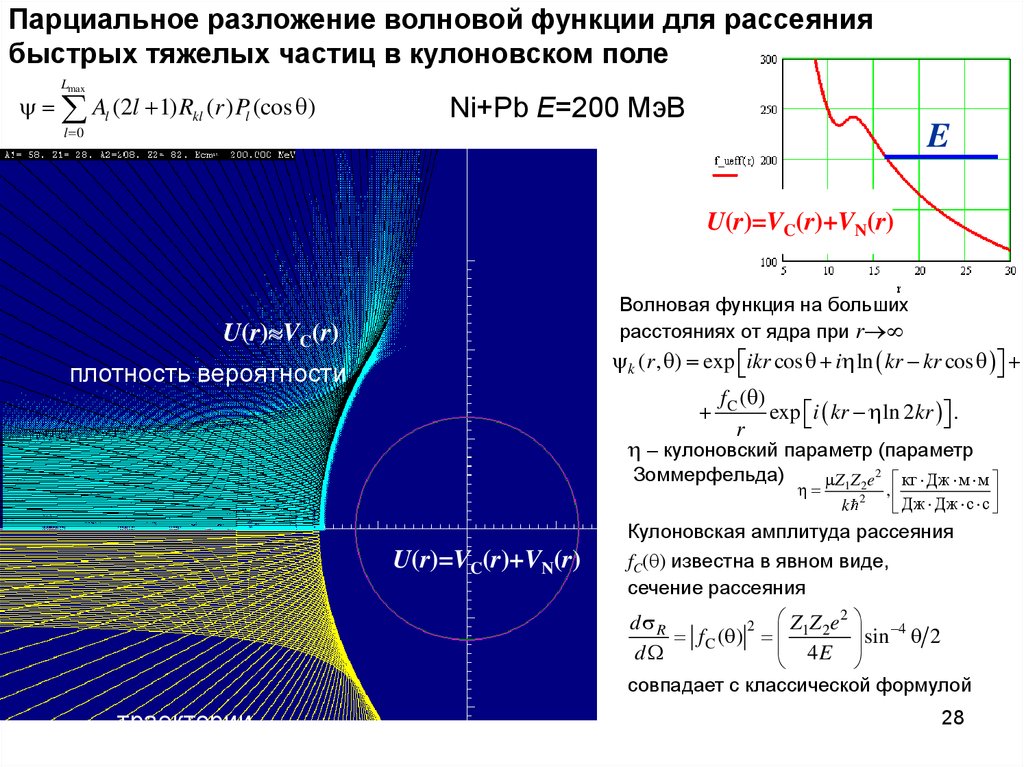
28. Парциальное разложение волновой функции для рассеяния быстрых тяжелых частиц в кулоновском поле

Lmax
Al (2l 1) Rkl (r ) Pl (cos )
Ni+Pb E=200 МэВ
E
l 0
U(r)=VC(r)+VN(r)
Волновая функция на больших
расстояниях от ядра при r
U(r) VC(r)
k (r , ) exp ikr cos i ln kr kr cos
плотность вероятности
+
f C ( )
exp i kr ln 2kr .
r
– кулоновский параметр (параметр
Зоммерфельда)
U(r)=VC(r)+VN(r)
Z1Z 2e 2 кг Дж м м
,
k 2
Дж Дж с с
Кулоновская амплитуда рассеяния
fC( ) известна в явном виде,
сечение рассеяния
Z1Z 2e 2 4
d sR
2
f C ( )
sin 2
dW
4
E
совпадает с классической формулой
траектории
28

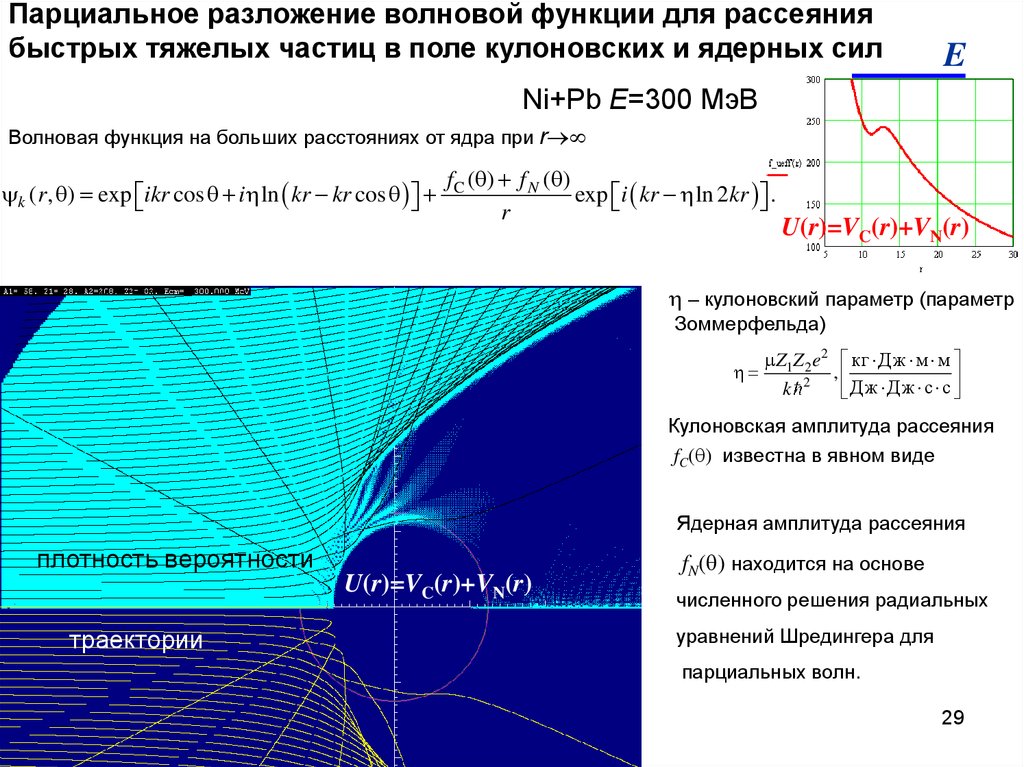
29. Парциальное разложение волновой функции для рассеяния быстрых тяжелых частиц в поле кулоновских и ядерных сил

E
Ni+Pb E=300 МэВ
Волновая функция на больших расстояниях от ядра при r
k (r , ) exp ikr cos i ln kr kr cos
f C ( ) f N ( )
exp i kr ln 2kr .
r
U(r)=VC(r)+VN(r)
– кулоновский параметр (параметр
Зоммерфельда)
Z1Z 2e 2 кг Дж м м
,
k 2
Дж Дж с с
Кулоновская амплитуда рассеяния
fC( ) известна в явном виде
Ядерная амплитуда рассеяния
плотность вероятности
U(r)=VC(r)+VN(r)
траектории
fN( ) находится на основе
численного решения радиальных
уравнений Шредингера для
парциальных волн.
29

30. Оптическая модель упругого рассеяния

Различные состояния, образующиеся после столкновения частиц, называют каналами реакции. Например,
при столкновении протона с ядром А возможны следующие каналы реакции:
p+A p+A (упругое рассеяние)
p+A* (неупругое рассеяние
с возбуждением ядра-мишени)
n+A (выбивание нейтрона)
А1+A2 (деление ядра)
другие каналы
При энергиях, превышающих порог неупругих
процессов, частица-снаряд может выйти из упругого
канала. При этом число упруго рассеянных частиц
всегда меньше, чем число частиц налетающих на
ядро-мишень.
В нерелятивистской квантовой механике уменьшение потока частиц может быть смоделировано
добавлением отрицательной мнимой части iW(r), W(r)<0, к потенциалу взаимодействия ядер V(r).
Нестационарное уравнение Шредингера
Уравнение непрерывности, описывающее
поглощение частиц
d
2
divj W (r ) 0
dt t
2
i
V (r ) iW (r ) (r , t )
t 2m
вектор плотности потока вероятности
плотность вероятности
(r , t ) *
Фешбах, 1954 г.
j (r , t )
m Im
2im
*
*
*
V (r ) VC (r ) VN (r ) W0 V0
W (r )
W0
объемное
r RW поглощение
1 exp
aW
(r RW ) 2
W (r ) W0 exp
2
b
поверхностное поглощение
NRV
30

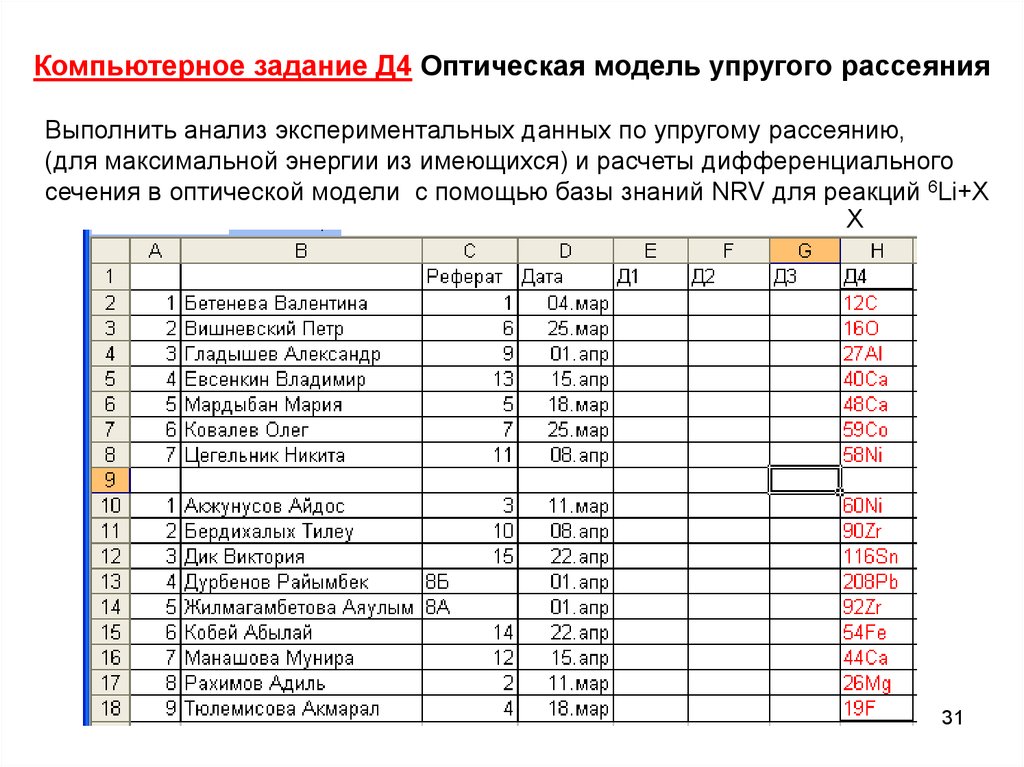
31. Компьютерное задание Д4 Оптическая модель упругого рассеяния

Выполнить анализ экспериментальных данных по упругому рассеянию,
(для максимальной энергии из имеющихся) и расчеты дифференциального
сечения в оптической модели с помощью базы знаний NRV для реакций 6Li+X
X
31

32. Компьютерное задание Д4 Оптическая модель упругого рассеяния

Сетевая база знаний NRV
по ядерной физике низких
энергий. URL: http://nrv.jinr.ru/
ЛЯР им. Г.Н. Флерова ОИЯИ
ОПТИЧЕСКАЯ МОДЕЛЬ УПРУГОГО
РАССЕЯНИЯ В БАЗЕ ЗНАНИЙ
NUCLEAR REACTION VIDEO (NRV)
Методические указания к
практическим и лабораторным
занятиям (на русском языке)
32

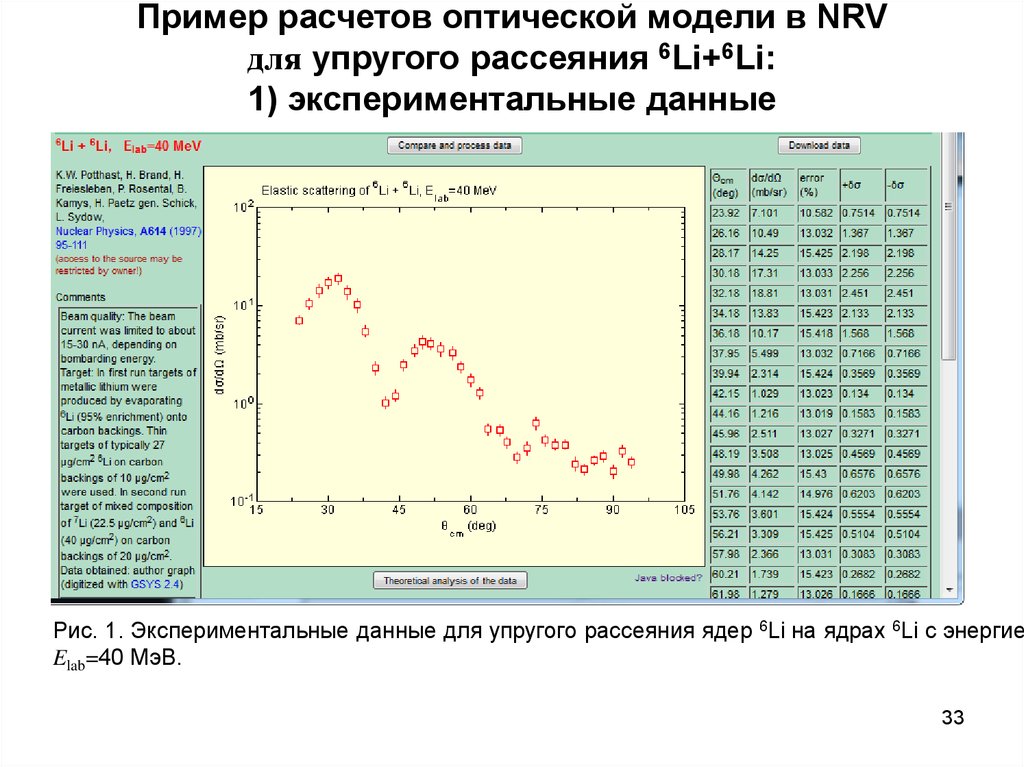
33. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 1) экспериментальные данные

Рис. 1. Экспериментальные данные для упругого рассеяния ядер 6Li на ядрах 6Li с энергие
Elab=40 МэВ.
33

34. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 2) ввод данных

Описание
Рис. 2. Форма для ввода данных для расчетов упругого рассеяния ядер 6Li на ядрах 6Li.
34

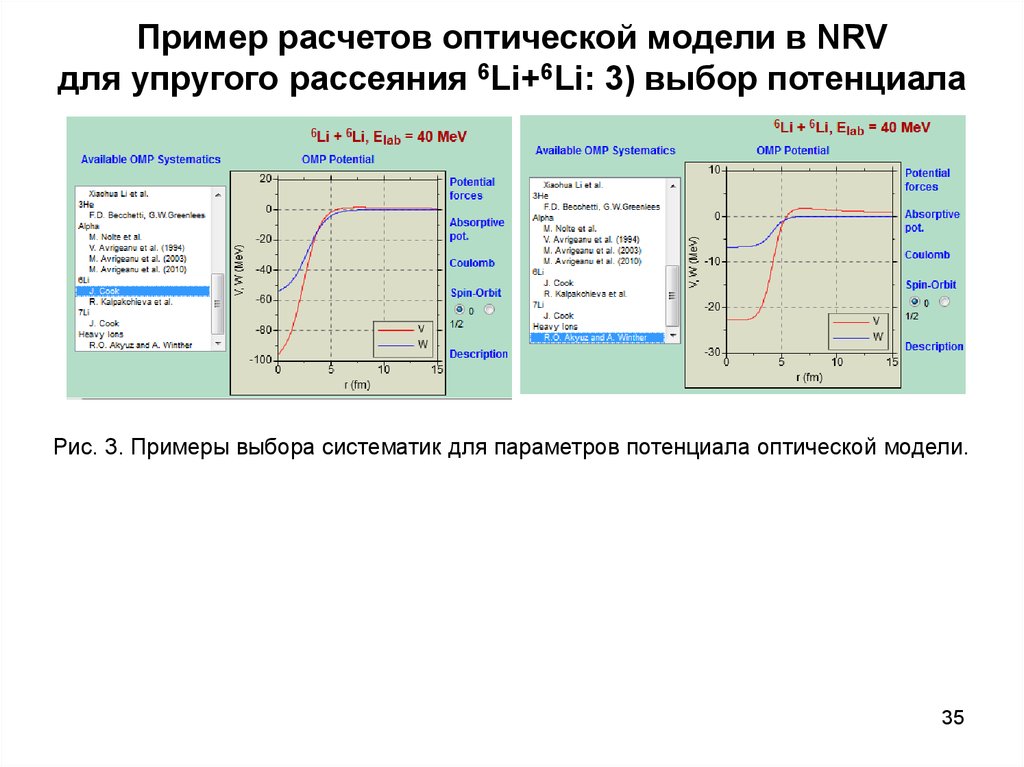
35. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 3) выбор потенциала

Рис. 3. Примеры выбора систематик для параметров потенциала оптической модели.
35

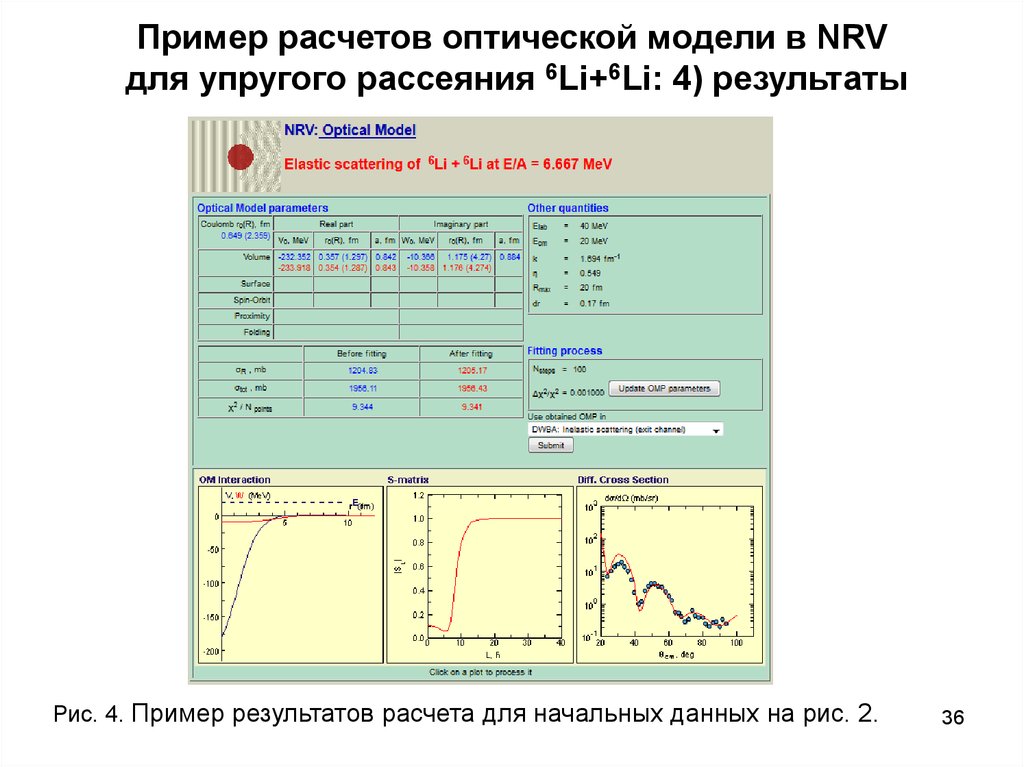
36. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 4) результаты

Рис. 4. Пример результатов расчета для начальных данных на рис. 2.
36

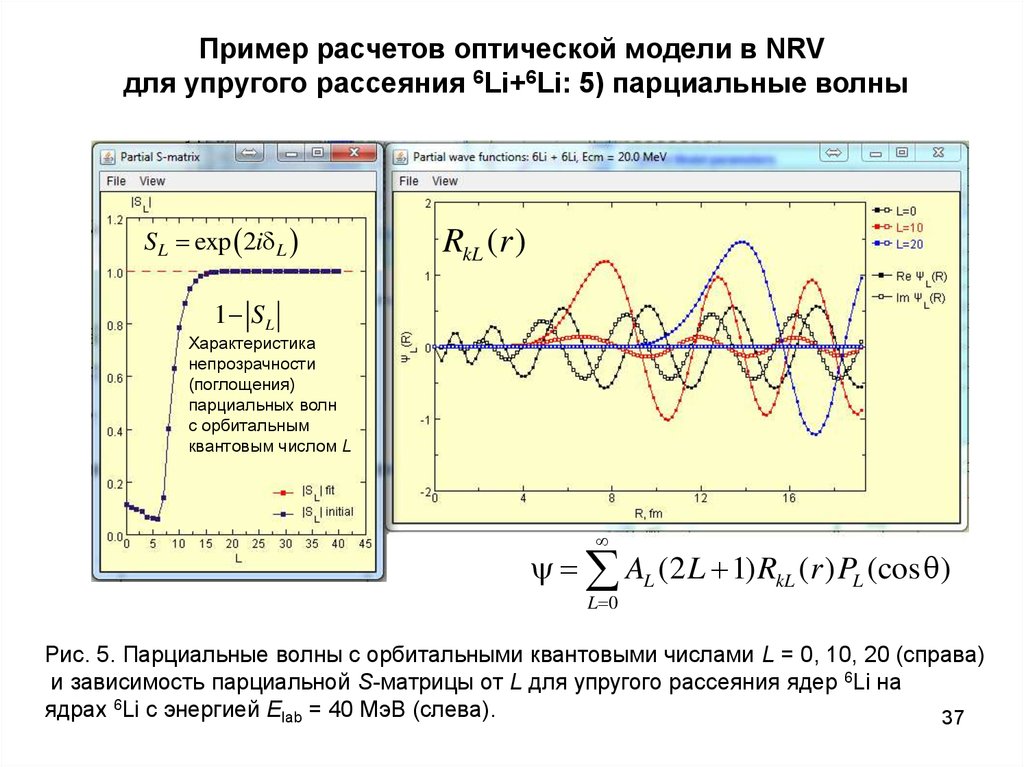
37. Пример расчетов оптической модели в NRV для упругого рассеяния 6Li+6Li: 5) парциальные волны

SL exp 2i L
RkL (r )
1 SL
Характеристика
непрозрачности
(поглощения)
парциальных волн
с орбитальным
квантовым числом L
AL (2 L 1) RkL ( r ) PL (cos )
L 0
Рис. 5. Парциальные волны с орбитальными квантовыми числами L = 0, 10, 20 (справа)
и зависимость парциальной S-матрицы от L для упругого рассеяния ядер 6Li на
ядрах 6Li с энергией Elab = 40 МэВ (слева).
37

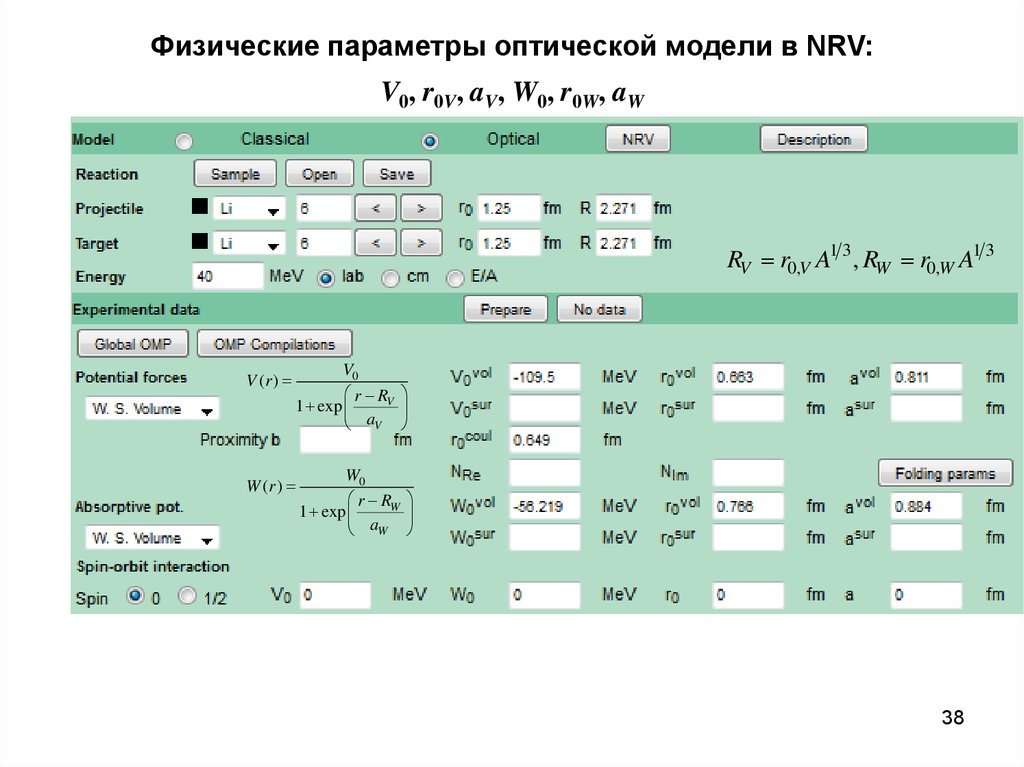
38. Физические параметры оптической модели в NRV: V0, r0V, aV, W0, r0W, aW

RV r0,V A1 3 , RW r0,W A1 3
V (r )
V0
r RV
1 exp
aV
W (r )
W0
r RW
1 exp
aW
38

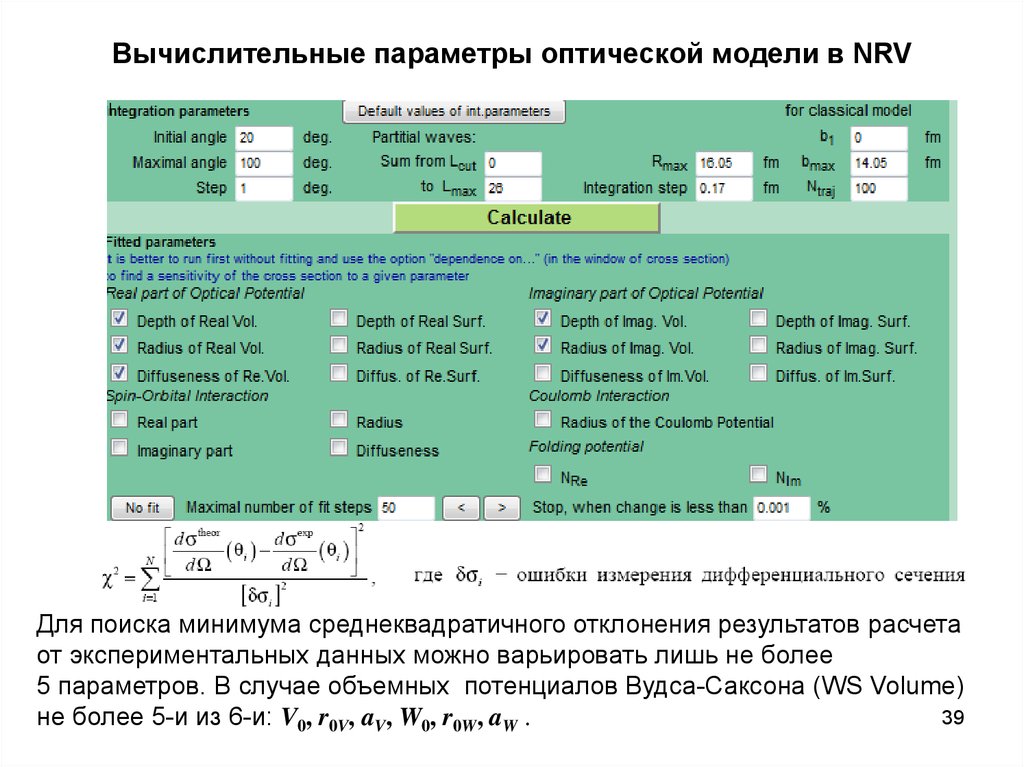
39. Вычислительные параметры оптической модели в NRV

I
Для поиска минимума среднеквадратичного отклонения результатов расчета
от экспериментальных данных можно варьировать лишь не более
5 параметров. В случае объемных потенциалов Вудса-Саксона (WS Volume)
39
не более 5-и из 6-и: V0, r0V, aV, W0, r0W, aW .

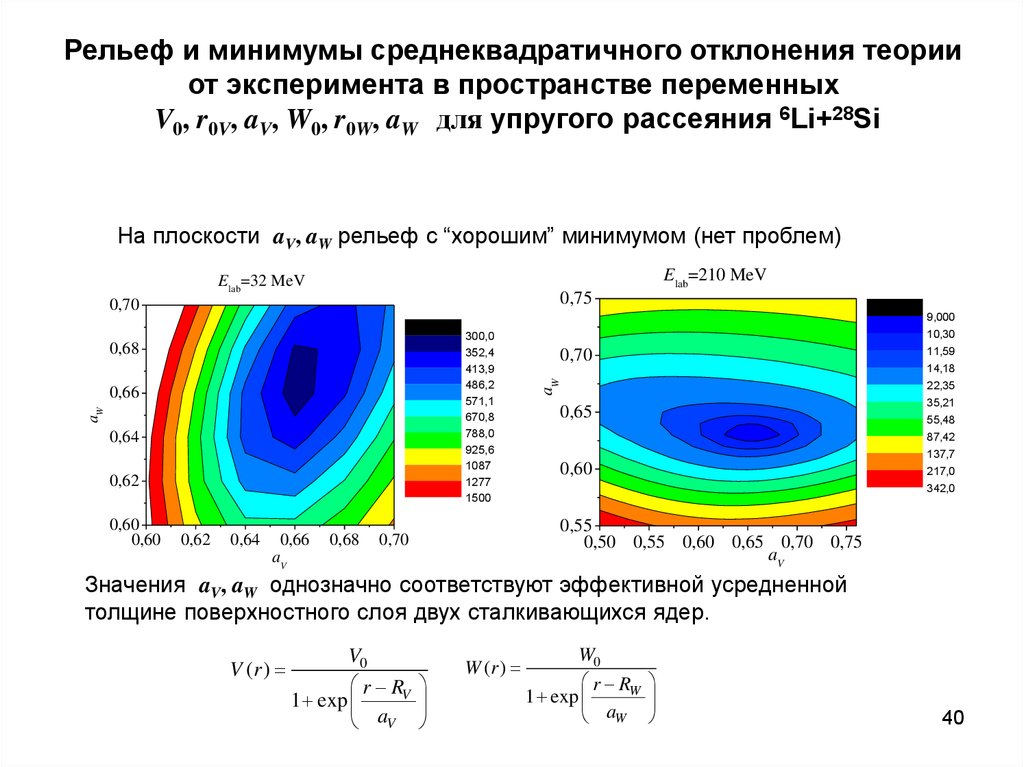
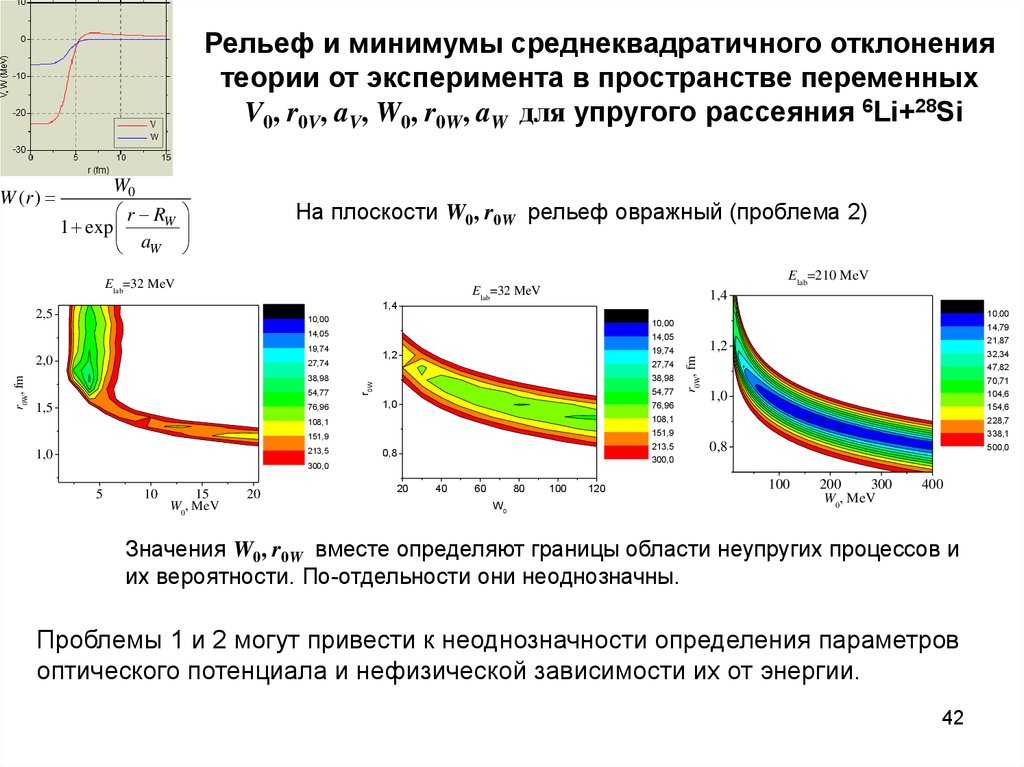
40. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W, aW для

упругого рассеяния 6Li+28Si
На плоскости aV, aW рельеф c “хорошим” минимумом (нет проблем)
Elab=210 MeV
Elab=32 MeV
0,75
0,70
9,000
0,68
aW
0,66
0,64
0,62
0,60
0,60
0,62
0,64
0,66
aV
0,68
10,30
0,70
aW
300,0
352,4
413,9
486,2
571,1
670,8
788,0
925,6
1087
1277
1500
0,65
11,59
14,18
22,35
35,21
55,48
87,42
137,7
0,60
217,0
342,0
0,55
0,50 0,55 0,60 0,65 0,70 0,75
aV
0,70
Значения aV, aW однозначно соответствуют эффективной усредненной
толщине поверхностного слоя двух сталкивающихся ядер.
V (r )
V0
r RV
1 exp
aV
W (r )
W0
r RW
1 exp
aW
40

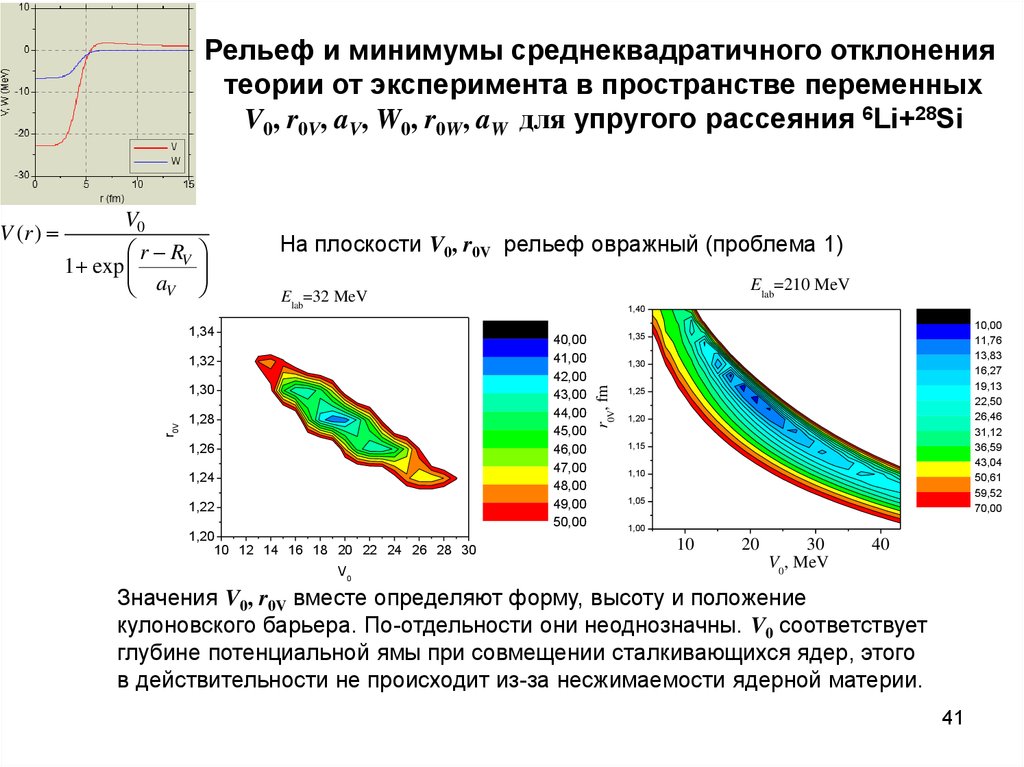
41. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W, aW для

упругого рассеяния 6Li+28Si
На плоскости V0, r0V рельеф овражный (проблема 1)
Elab=210 MeV
Elab=32 MeV
1,34
1,40
40,00
41,00
42,00
43,00
44,00
45,00
46,00
47,00
48,00
49,00
50,00
1,32
1,30
1,28
1,26
1,24
1,22
1,20
10 12 14 16 18 20 22 24 26 28 30
V0
10,00
11,76
13,83
16,27
19,13
22,50
26,46
31,12
36,59
43,04
50,61
59,52
70,00
1,35
1,30
r0V, fm
V0
r RV
1 exp
aV
r0V
V (r )
1,25
1,20
1,15
1,10
1,05
1,00
10
20
30
V0, MeV
40
Значения V0, r0V вместе определяют форму, высоту и положение
кулоновского барьера. По-отдельности они неоднозначны. V0 соответствует
глубине потенциальной ямы при совмещении сталкивающихся ядер, этого
в действительности не происходит из-за несжимаемости ядерной материи.
41

42. Рельеф и минимумы среднеквадратичного отклонения теории от эксперимента в пространстве переменных V0, r0V, aV, W0, r0W, aW для

упругого рассеяния 6Li+28Si
W0
r RW
1 exp
aW
На плоскости W0, r0W рельеф овражный (проблема 2)
Elab=32 MeV
1,4
2,5
14,05
14,05
54,77
76,96
27,74
38,98
54,77
1,0
76,96
108,1
108,1
151,9
151,9
213,5
213,5
0,8
10
15
W0, MeV
20
20
21,87
32,34
47,82
70,71
104,6
1,0
154,6
228,7
338,1
0,8
500,0
300,0
300,0
5
14,79
1,2
19,74
1,2
r0W
r0W, fm
38,98
1,0
10,00
10,00
27,74
1,5
1,4
10,00
19,74
2,0
Elab=210 MeV
Elab=32 MeV
r0W, fm
W (r )
40
60
80
W0
100
120
100
200
300
W0, MeV
400
Значения W0, r0W вместе определяют границы области неупругих процессов и
их вероятности. По-отдельности они неоднозначны.
Проблемы 1 и 2 могут привести к неоднозначности определения параметров
оптического потенциала и нефизической зависимости их от энергии.
42

43. Литература

1.
2.
3.
Ландау Л.Д. Лифшиц Е.М. Краткий курс
теоретической физики. Т. 2. Квантовая механика. −
М. Наука. 1971.
Фрауэнфельдер, Г. Субатомная физика. /Г.
Фрауэнфельдер, Э. Хэнли. – М.: Мир. 1979.
Nuclear Reaction Video. База знаний по
низкоэнергетическим ядерным реакциям.
4.
http://nrv.jinr.ru/nrv/.
5.
Н.Мотт, Г.Месси. Теория атомных столкновений. М.:
Мир, 1969,.
43

44. Вопрос 9.

• Стационарная теория возмущений в
отсутствие вырождения.
• Стационарная теория возмущений при
наличии вырождения.
• Эффект Зеемана.
• Эффект Штарка.
44

45. Стационарная теория возмущений в отсутствие вырождения

Hˆ Vˆ E Формулы 12
c V c ; V Vˆ dq
Hˆ Hˆ 0 Vˆ ; Hˆ 0 (0) E (0) (0) ;
cm (0)
m ;
(0)
E
E
k
m
0
k
km m
(0)*
k
km
(0)
m
m
Поправки к энергии первого порядка в невырожденном случае
(0)
(1)
(1)
n
n
k
kn
k
E E
ˆ (0) dq
E ; c c ; for k n : En(1) Vnn (0)*
V
n
n
Vkn
Vmn
(1)
(1)
(0)
(0)
;
с
0;
n
n
m
(0)
(0)
(0)
En Ek
m n En Ek
for k n : с
(1)
k
Условие применимости поправки к энергии первого порядка
Vmn E
(0)
n
E
(0)
k
(2)
n
; E
m n
Vmn
(0)
n
E
2
E
(0)
k
(2)
0
; E
m n
Vmn
(0)
0
E
2
E
(0)
k
0
45

46. Стационарная теория возмущений при наличии вырождения

(0) (0)
ˆ (0) E (0) (0) ,
Hˆ Hˆ 0 Vˆ ; Hˆ 0 (0)
E
;
H
n
n
n
0 n
n
n
Hˆ
ˆ E
V
0
Формулы 12
cm (0)
m ;
m
(0)
(0)* ˆ (0)
E
E
c
V
c
;
V
k k km m km k V m dq
m
E En(0) En(1) ; cn cn(0) , cn cn(0)
,
En(1) cn Vnn cn(0)
;
n
; для En(0) En(0)
: ck 0, для Ek(0) En(0)
секулярное уравнение
(1)
(0)
(1)
V
E
c
0;
V
E
nn n nn n
nn
n nn 0
n
Поправки к энергии первого порядка в невырожденном и вырожденном случаях
46

47. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета спина)

2
2
1
q
1
q
ˆ A U ; A 1 Hr , q e
ˆ
H
p
A
q
;
H
p
2m
c
2m
c
2
2
e
e
e
2
ˆ Hˆ Lˆ H,
ˆ
Hˆ H 0
A
p
A
H
H
r
p
a a 2mc 2 a a 0 2mc a a a 0 B
mc a
L
Магнетон Бора
e
ˆ
Vˆ B LH= B HLˆz , B
cM (0)
M
2
mc
оператор взаимодействия
Н
M L
z
Поправка к энергии состояния с орбитальным моментом L по формуле для наличия
вырождения по орбитальному магнитному квантовому числу M = –L,…L
* ˆ (0)
(0) * ˆ
(0)
(0) *
(0)
VM M (0)
V
dq
H
L
dq
H
M
LM
LM
B
LM
z LM
B
LM
LM dq
B HM M M
VM M EM(1) M M 0
Формулы 13
Поправка к энергии по формуле для отсутствия вырождения
E En(0) En(1) ; En(1) E B H Lz = B HM L ; M L L,
расщепление уровней в 1 порядке теории возмущений.
L 0 : En(1)
B HM M M EM(1) M M 0
L, B
e
2mc
2
2
2
e2
e
e
2
2
2
0, E
A
H
r
H
r
;
a
a
a
2
2
2
2mc a
8mc a
12mc
a
47

48. Эффект Зеемана – расщепление спектральных линий и уровней энергии атома в однородном магнитном поле (без учета спина)

E En(0) En(1) ; En(1) E B HM L ; M L L,
L
расщепление уровней в 1 порядке теории возмущений.
Расщепление синглетных энергетических уровней атома
кадмия на 2L+1 подуровней в магнитном поле и переходы,
разрешенные правилами отбора ML=0,±1
Разность энергий между соседними подуровнями одинакова
для всех синглетных (с нулевым спином) уровней
Расщепление в магнитном поле линий спектра на
три компоненты называется простым эффектом
Зеемана
Рис. к формулам 13
поляризация - и s-компонент зеемановского триплета
Простой эффект Зеемана
(без учета спина) для
S=0 в слабом поле или с
учетом спина в сильном поле
48

49. Эффект Зеемана – расщепление красной спектральной линии атома кадмия в однородном магнитном поле (без учета спина)

Изображение интерференционной картины
на экране компьютера с без магнитного поля.
Использован интерферометр Фабри-Перо.
Изображение интерференционной картины
на экране компьютера для простого
“поперечного” эффекта Зеемана
Наблюдения спектров излучения чаще всего производят по нормали к направлению магнитного поля
(“поперечный” эффект Зеемана) или по направлению поля (“продольный” эффект Зеемана).
При продольном эффекте Зеемана видны только смещенные s-компоненты зеемановского триплета,
которым соответствует циркулярно поляризованный свет. Двум направлениям круговой поляризации
(по и против часовой стрелки) соответствуют два возможных значения проекции момента импульса
фотона на направление движения и два значения проекции спина фотона. При наблюдении поперек поля
эти линии оказываются линейно поляризованными. Вектор напряженности электрического поля E
колеблется перпендикулярно направлению магнитного поля . Несмещенная -компонента не видна при
наблюдении вдоль поля, а при наблюдении поперек поля линейно поляризована, причем вектор E 49
колеблется вдоль направления магнитного поля .

50. Эффект Штарка - расщепление спектральных линий и уровней энергии в однородном электрическом поле

V Ed E d z
1. Атом водорода: линейный эффект Штарка
En(1) cn Vnn cn(0)
;
n
(1)
(0)
(1)
V
E
c
0;
V
E
nn n nn n
nn
n nn 0
n
2. Сложный атом: квадратичный эффект Штарка
ˆ (0) dq 0
E En(0) En(1) ; ck kn ck(1) ; k n : En(1) Vnn (0)*
V
n
n
Vmn E
(0)
n
E
(0)
k
(2)
n
; E
m n
Vmn
(0)
n
E
2
E
(0)
k
(2)
0
; E
m n
Vmn
(0)
0
E
2
E
(0)
k
0
Эффект Штарка:
1. Линейный у атома водорода и водородоподобных атомов (в слабых полях), связан с
вырождением уровней энергии по орбитальному квантовому числу в кулоновском поле.
Средний дипольный момент таких атомов не равен нулю. Энергия подуровней зависит от
главного квантового числа, орбитального квантового числа и модуля магнитного
орбитального квантового числа. Например состояние с n =2 расщепляется на 3 подуровня, в
общем случае на 2n -1 подуровень.
2. Квадратичный у атома водорода и водородоподобных атомов в сильных полях, у
многоэлектронных атомов с нулевым средним дипольным моментом.
50

51. Литература

1.
2.
Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и
ядерная физика: учеб. пособие– М.: Физматлит, 2002
Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М. Наука. 1971
.
51

52. Вопрос 10

Уравнение Дирака.
Квазирелятивистское приближение.
Спин-орбитальное взаимодействие.
Тонкая структура спектра атома водорода
и атомов щелочных элементов.
52

53. Уравнение Дирака

Формулы 14
для свободного движения
i
Матрицы Паули
capˆ mc 2b ; ; 1 ; 3 ;
t
2
4
0 s
I 0
0 1
0 i
1 0
a
; b
; s1
; s2
; s3
;
s 0
0 I
1 0
i 0
0 1
Состояния с определенным значением импульса p и энергии
mc 2 csp 0 mc 2
csp
;
0; c p 2 m2 c 2
2
2
csp mc
csp mc 0
положительные и
отрицательные “частоты”
q
Движение в электромагнитном поле pˆ pˆ A; qA0
c
ˆ q
2
2
cs p c A qA0 mc
cs pˆ q A qA mc 2
0
c
Оператор полного момента
cspˆ mc
2
ˆ
csp mc
в центральном поле
ˆj lˆ sˆ
Операторы проекций внутреннего
углового момента (спинового момента)
sˆ
2
s
Оператор спина
для электрона
q = –e<0
qA0= –e2/r
1
sˆ s sˆ1 , sˆ2 , sˆ3
2
для атома водорода
cspˆ mc 2 e2 r
2
2
cspˆ mc e r
Шаровые спиноры – собственные функции
ˆj 2 , lˆ2 , ˆjz2
l m 1 2
l m 1 2
Y
l , m 1 2
f
(
r
)
W
Y
j ,l , m
l , m 1 2
2l 1
l j 1 2;
2
l
1
W
1 l l
;
l 1 2, l , m
l m 1 2
Wl 1 2,l , m
l
2
j
l
;
2
j m 1 2
( 1)
g ( r )W j , l , m
Yl , m 1 2
Yl , m 1 2
2l 1
2
l
1
1
f mc 2 1e 2 Q Q
1
2
1
1
2
2
j 1 2 (l 1), j l 1 2;
f
f
mc
e
r
g
0
2
1 2
r
c
g mc e Q1 Q2 0
j 1 2 l , j l 1 2;
1
1
g
g mc 2 e 2 r f 0 2 r ; ( ) m 2 c 2 2 c 2 ; 2 a 2
0,1, 2, , 0, j l 1 2;
r
c
nr
a
1, 2,3, , 0, j l 1 2;
nr
; целое положительное число
53
c ( )
Берестецкий В.Б. Лифшиц Е.М., Питаевский Л.П. Квантовая электродинамика

54. Решения уравнения Дирака для атома водорода: уровни энергии

j 1 2 (l 1), j l 1 2;
j 1 2 l , j l 1 2;
0,1, 2,
nr
1, 2,3,
, 0, j l 1 2;
, 0, j l 1 2;
e2
1
a
4 0 c 137
СИ
e2
1
a
c 137
Гауссова система единиц
точное выражение
mc 2
1
n
r
mc 2 E (nr , j )
a2
a
2
2
2
приближенное выражение
2
1 e2 a 2 1
3
E (n, j ) 2
; aB 2
1
n 2aÁ
n j 1 2 4n
me
54

55. Решение уравнения Дирака для атома водорода: энергии

2
1 (СИ)
e2
1
, 0, j l 1 2; a e
a
4 0 c 137
c 137
, 0, j l 1 2;
0,1, 2,
j 1 2 (l 1), j l 1 2;
nr
j 1 2 l , j l 1 2;
1, 2,3,
1
E (nr , j ) mc 2 mc 2 (
1
точное
выражение
n
r
1
mc 2 (
1
a
a
2
a
2
2
nr a 2 (2 )
2
1
mc 2 (
1
a
n
r
2
2
1
2
1 2 a
2
(2 (nr )
n
r
a
1)
2
1 a
2
2
1
1) mc 2 (
2
1
1) mc 2 (
1
a
(Гауссова)
2
приближенные
выражения
1)
2
nr 1 a 2 (2 (nr )
2
2
1)
2
2
2
a
1
2
a
mc 2
1 2 a 2 (2 (nr )
1 2 a 2 (2 (nr )
2
2
2 n
3 4 nr
r
приближенное выражение
mc a
2
2
2 nr
2
1
a2
3
1
me 4
2 2
; nr n; j ; mc a 2
1
2
nr 4 nr
Энергия уровней атома водорода с учетом тонкой структуры
2
1 e a2 1
3
E (n, j ) 2
; aB 2
1
n 2aB
n j 1 2 4n
me
2
Формулы 15
55

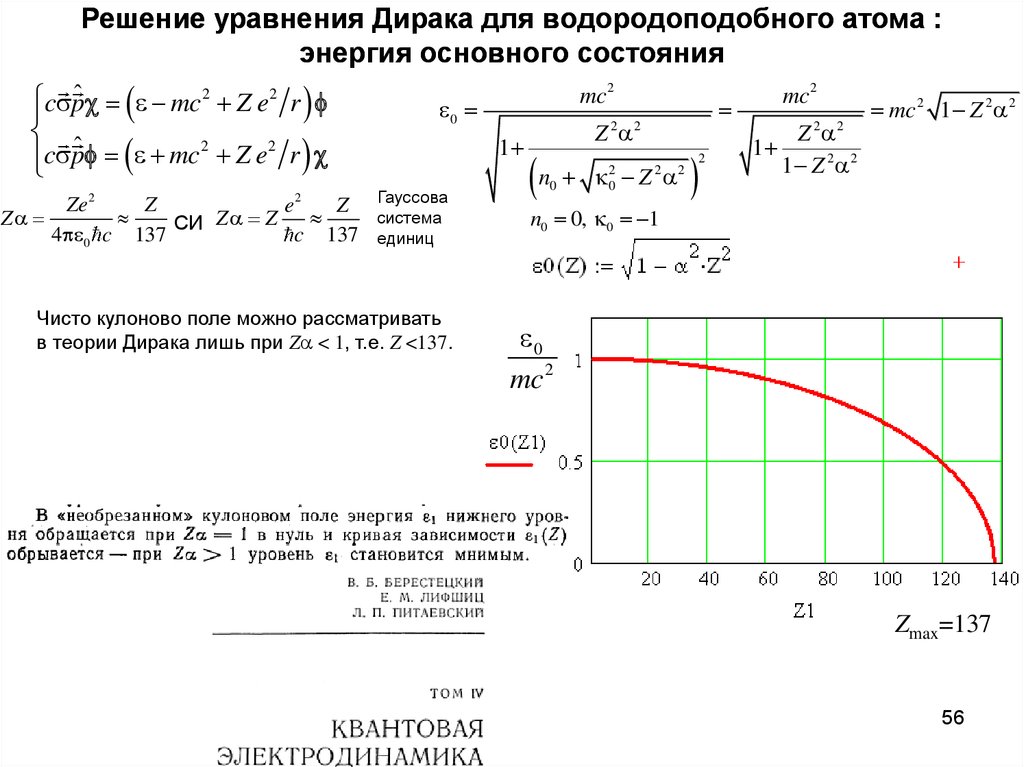
56. Решение уравнения Дирака для водородоподобного атома : энергия основного состояния

cspˆ mc 2 Z e2 r
2
2
cspˆ mc Z e r
Za
2
2
Ze
Z
e
Z
СИ Z a Z
4 0 c 137
c 137
mc 2
0
1
Гауссова
система
единиц
Чисто кулоново поле можно рассматривать
в теории Дирака лишь при Za < 1, т.е. Z <137.
n
0
Z 2a2
Z a
2
0
2
2
2
mc 2
Z 2a2
1
1 Z 2a2
mc 2 1 Z 2 a 2
n0 0, 0 1
0
mc 2
Zmax=137
56

57.

Решение уравнения Дирака для водородоподобного атома с ядром
конечного размера: энергия основного состояния
57

58. Квазирелятивистское приближение.

2
2
Нерелятивистское движение в слабом электромагнитном поле E mc ; E qA0 mc
q
2
cs p c A qA0 mc
cs p q A qA mc 2
0
c
для электрона q = –e<0
qA0=V(r)
2
q
q
1
sH
p A qA0
2
m
c
2
mc
E ; H rotA;
Уравнение Паули
магнетон Бора
q
q
e
1
ˆ e , sˆ 1 s.
sH ˆ H 2 B sˆ H, ˆ
s
2 s 2 B s,
B
2mc
2mc
2mc
2
2mc
2
– оператор спинового магнитного момента, s – оператор спина электрона
Движение в слабом центральном электростатическом поле eA0=V(r)
с точностью до членов порядка v2/c2
1 ˆ2
p V (r ) Wˆ1 Wˆ2 Wˆ3 E
2m
W1
2
8m 2 c 2
V
[ E V ]
2
W2
W3
2mc 2
Оператор
контактного
взаимодействия
E g E ( gH g 1 ) g H
pˆ 2
g 1
4m 2 c 2
В кулоновском поле V(r)= e2Z/r
12
pˆ 2
1
2 2
8m c
W1
2
2 2
8m c
V
2
2 2
8m c
4 Ze 2 (r )
Поправка к оператору кинетической энергии,
из-за изменения массы частицы при
изменении ее скорости
1 V ˆ ˆ Äæ ñ Äæ êã ì
V pˆ
s
sL
,
Äæ
Äæ êã ì ñ
2m2 c 2 r r
4m 2 c 2
Формулы 16
Формулы 16
Оператор спин-орбитального
взаимодействия
58

59. Спин-орбитальное взаимодействие.

Спин-орбитальное взаимодействие
.
Формулы 15
резкая серия
главная серия
Водород E=4*10-5 эВ
59
Схема образования дублетных линий
главной и резкой серий натрия

60. Спин-орбитальное взаимодействие.

Спин-орбитальное взаимодействие
.
резкая серия
главная серия
Схема образования дублетных линий
главной и резкой серий натрия
60

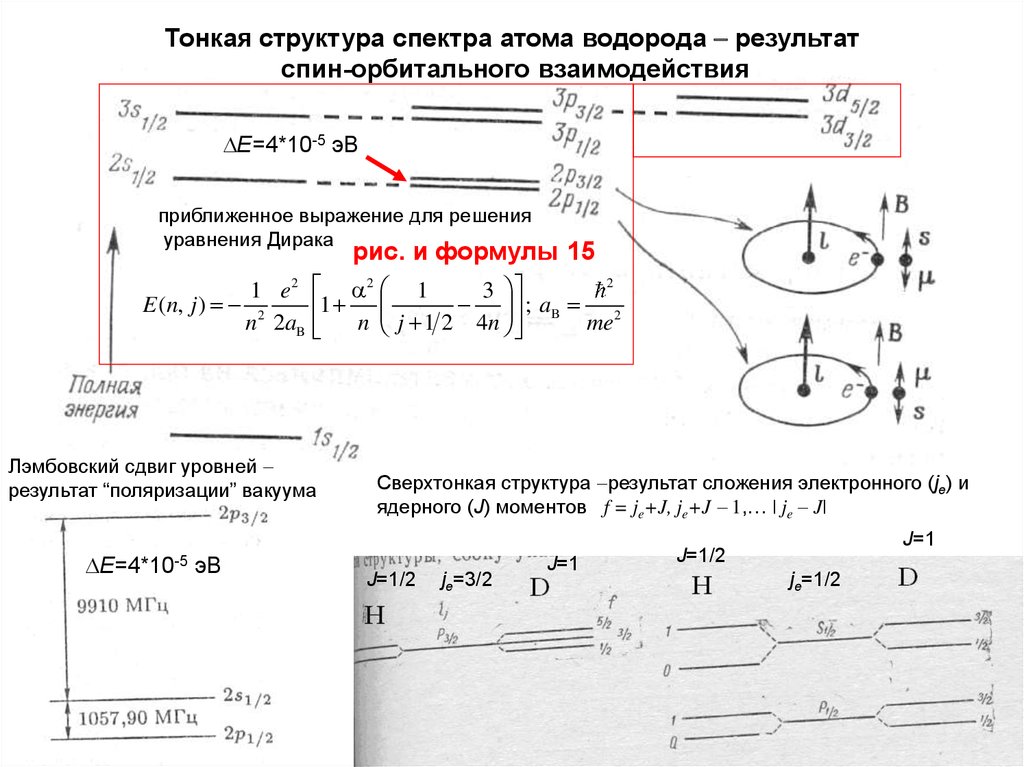
61. Тонкая структура спектра атома водорода  результат спин-орбитального взаимодействия

Тонкая структура спектра атома водорода результат
спин-орбитального взаимодействия
E=4*10-5 эВ
приближенное выражение для решения
уравнения Дирака
рис. и формулы 15
2
1 e2 a 2 1
3
E (n, j ) 2
; aB 2
1
n 2aB
n j 1 2 4n
me
Лэмбовский сдвиг уровней
результат “поляризации” вакуума
E=4*10-5 эВ
Сверхтонкая структура результат сложения электронного (je) и
ядерного (J) моментов f = je+J, je+J 1,… | je J|
J=1/2
je=3/2
J=1
J=1
J=1/2
je=1/2
61

62. Литература

1.
2.
Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и
ядерная физика: учеб. пособие– М.: Физматлит, 2002
Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М.: Наука. 1971
.
3.
Давыдов А.С. Квантовая механика. − М.: Наука. 1971.
4.
Карякин Н.И., Быстров К.Н., Киреев П.С. Краткий справочник
по физике. − М.: Высшая школа. 1969.
62

63. Вопрос 11.

Системы тождественных частиц.
Бозоны и фермионы.
Принцип Паули.
Атом гелия.
63

64. Принцип неразличимости одинаковых частиц в квантовой механике

В силу принципа неопределенности
невозможно проследить за каждой
из одинаковых частиц и различать
их.
антисимметричная
волновая функция
симметричная
волновая функция
Волновая функция системы двух
частиц (x,y) либо антисимметрична
A(x,y) = – A(y,x),
либо симметрична S(x,y) = S (y,x)
в силу того, что | (x,y)|2 = | (y,x)|2,
(x,y) = C (y,x)=C2 (x,y)
и С2=1, С=±1.
y
x
64
x

65. Системы тождественных частиц

Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М. Наука. 1971.
65

66.

Бозоны и фермионы: связь спина со статистикой
О частицах, описывающихся антисимметричными волновыми функциями,
говорят как о подчиняющихся статистике Ферми-Дирака или о фермионах,
а о частицах, описывающихся симметричными функциями – как
подчиняющихся статистике Бозе-Эйнштейна или о бозонах.
В релятивистской квантовой механике естественные физические
требования автоматически приводят к тому, что частицы со спином ½
подчиняются статистике Ферми. Из этого следует и общее утверждение:
все частицы с полуцелым спином являются фермионами,
а частицы с целым спином (в том числе со спином 0) – бозонами.
66

67. Вторичное квантование: спин и статистика

В релятивистской квантовой теории полная энергия сохраняется, масса и полное число частиц
не сохраняются. Релятивистская теория частиц – это теория с бесконечным числом степеней свободы,
подобная теории поля.
Математический аппарат для описания систем с переменным числом частиц – вторичное квантование,
в котором независимыми переменными являются числа заполнения различных состояний частицы.
Оператор квантованной волновой функции ( -оператор) разлагается по полному набору состояний
свободной частицы (плоским волнам) с положительными и отрицательными “частотами”. :
.
операторы рождения
1
ˆ
ˆ
ˆ
ˆ
a p , bp частиц и античастиц,
aˆ p u ( , p) exp i ( t pr ) bp u ( , p) exp i ( t pr )
ˆ
W
1
p
W
aˆ p u * ( , p) exp i ( t pr ) bˆp u * ( , p) exp i ( t pr )
p
В аппарате вторичного квантования гамильтониан системы частиц Н
получается из гамильтониана одной частицы Н(1) как интеграл
aˆ p , bˆp
операторы уничтожения
частиц и античастиц
с импульсами р и
энергиями
ˆ Hˆ (1)
ˆ dV
Hˆ
67
р

68. Бозоны и фермионы: спин и статистика

См. файл спин и статистика.pdf
Формулы 17
Формулы 17
68

69.

Бозоны и фермионы
См. файл частицы.pdf
69

70. Принцип Паули

70

71. Система двух электронов

Полная антисимметричная (по отношению к перестановке электронов) волновая
функция системы двух электронов может быть представлена в виде
произведения спиновой и координатной частей.
Состоянию со спином S=1 отвечает симметричная (по отношению к
перестановке электронов) спиновая волновая функция, следовательно
координатная часть является антисимметричной.
Состоянию со спином S=0 отвечает антисимметричная (по отношению к
перестановке электронов) спиновая волновая функция, следовательно
координатная часть является симметричной.
В состоянии со спином S=1 и антисимметричной координатной волновой
функцией электроны располагаются в среднем дальше друг от друга, чем
в состоянии со спином S=0 и симметричной координатной волновой
функцией. Поэтому при S=1 энергия отталкивания электронов меньше, чем
при S=0.
Значение энергии системы зависит от ее полного спина. На этом основании можно
говорить о некотором своеобразном взаимодействии частиц, приводящем к
этой зависимости. Это взаимодействие называют обменным. Оно представляет
собой чисто квантовый эффект, полностью исчезающий (как и сам спин) при
предельном переходе к классической механике.
Первое правило Хунда: Наименьшей энергией обладает терм с наибольшим
возможным значением S.
71

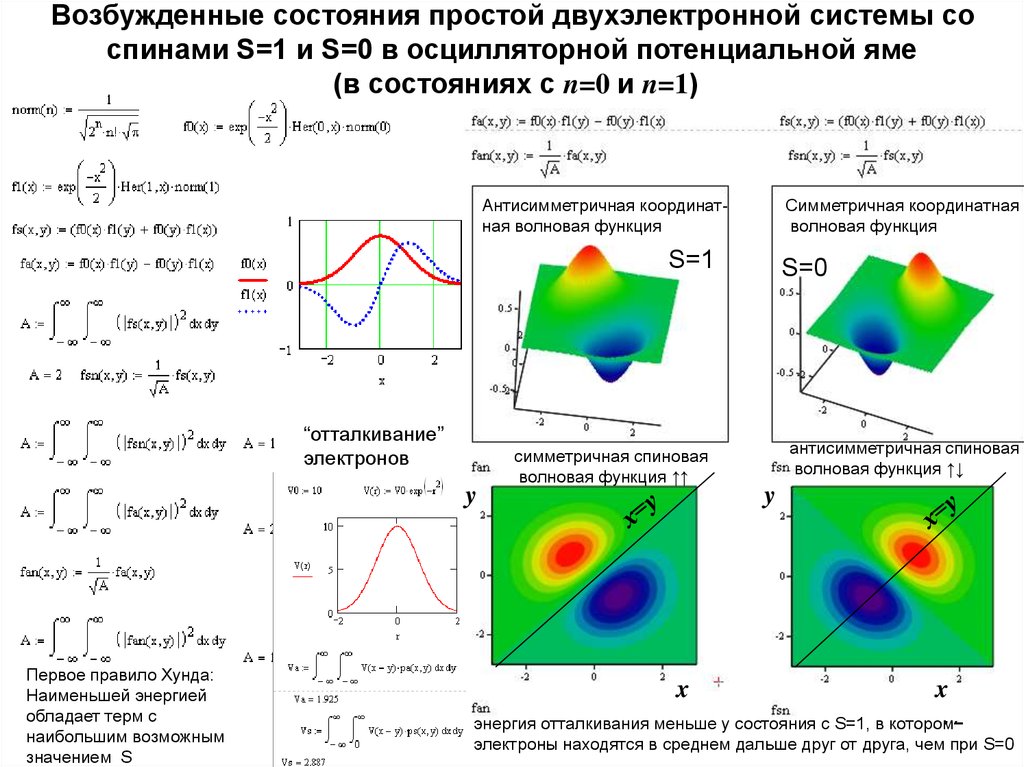
72. Возбужденные состояния простой двухэлектронной системы со спинами S=1 и S=0 в осцилляторной потенциальной яме (в состояниях с

n=0 и n=1)
Антисимметричная координатная волновая функция
Симметричная координатная
волновая функция
S=1
“отталкивание”
электронов
y
Первое правило Хунда:
Наименьшей энергией
обладает терм с
наибольшим возможным
значением S
симметричная спиновая
волновая функция ↑↑
x
S=0
антисимметричная спиновая
волновая функция ↑↓
y
x
72
энергия отталкивания меньше у состояния с S=1, в котором
электроны находятся в среднем дальше друг от друга, чем при S=0

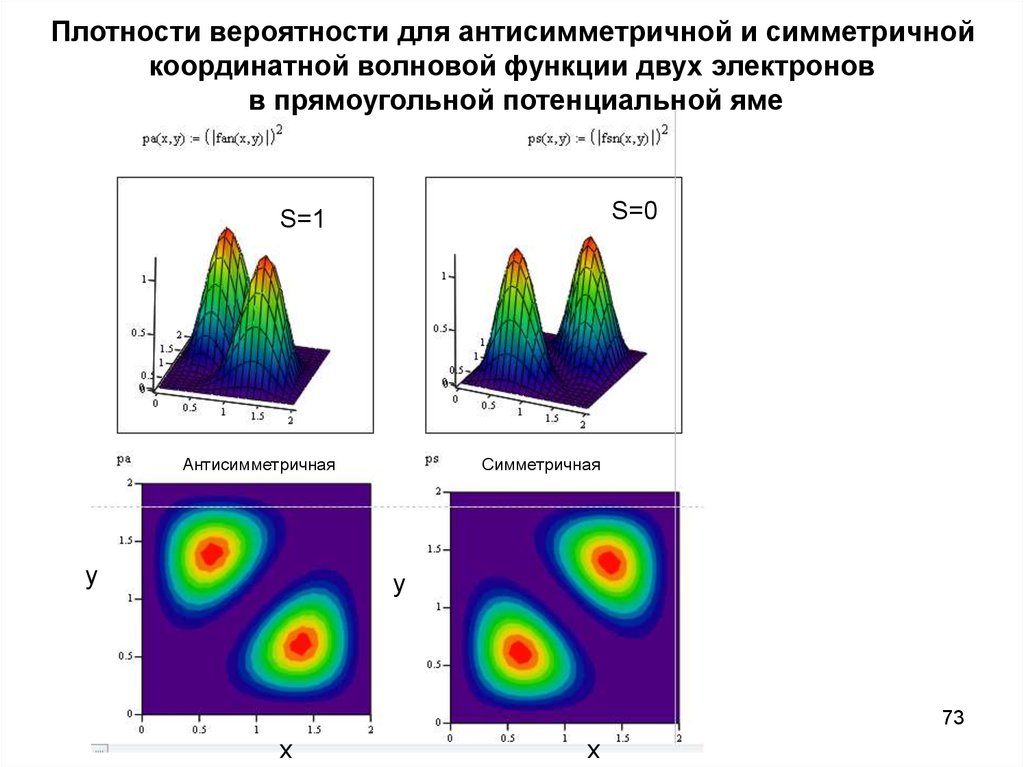
73. Плотности вероятности для антисимметричной и симметричной координатной волновой функции двух электронов в прямоугольной

потенциальной яме
S=0
S=1
Антисимметричная
y
Симметричная
y
73
x
x

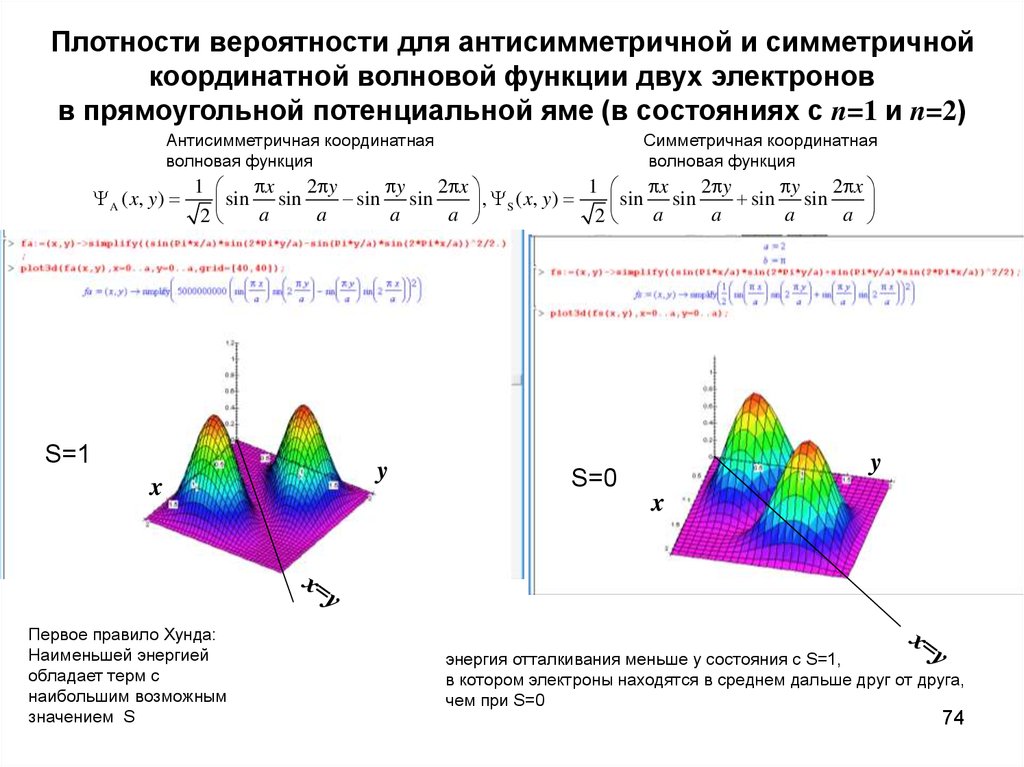
74. Плотности вероятности для антисимметричной и симметричной координатной волновой функции двух электронов в прямоугольной

потенциальной яме (в состояниях с n=1 и n=2)
Антисимметричная координатная
волновая функция
A ( x, y )
Симметричная координатная
волновая функция
1
x
2 y
y
2 x
1
x
2 y
y
2 x
sin sin
sin sin
sin sin
, S ( x, y )
sin sin
a
a
a
a
a
a
a
a
2
2
S=1
x
Первое правило Хунда:
Наименьшей энергией
обладает терм с
наибольшим возможным
значением S
y
y
S=0
x
энергия отталкивания меньше у состояния с S=1,
в котором электроны находятся в среднем дальше друг от друга,
чем при S=0
74

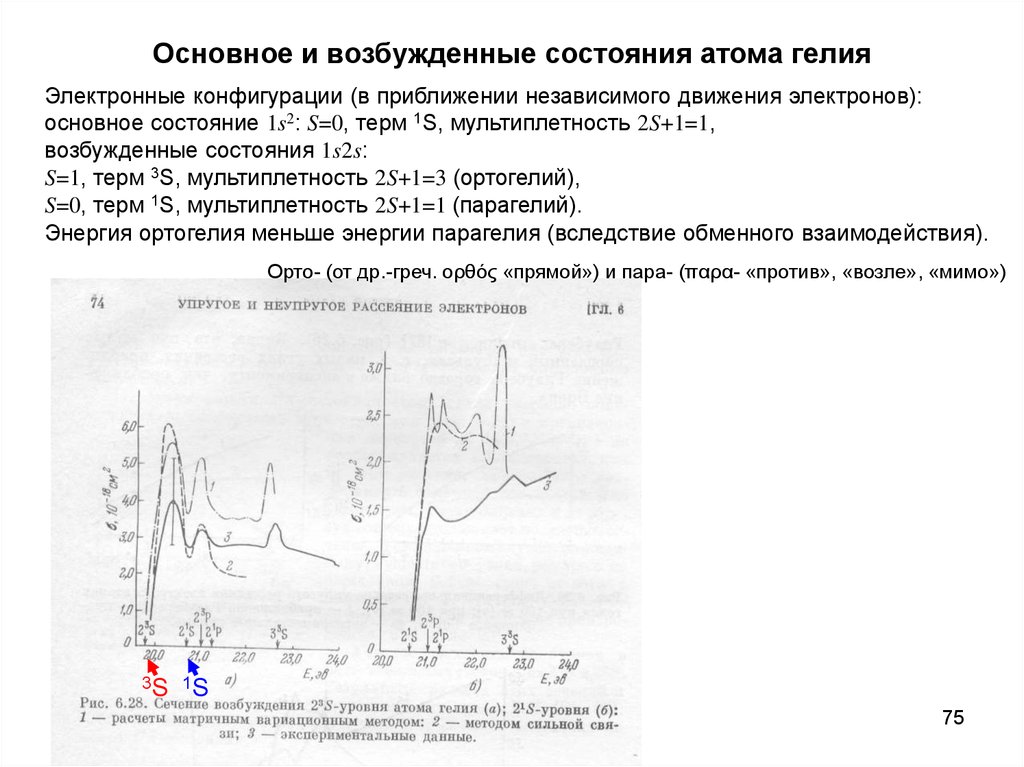
75. Основное и возбужденные состояния атома гелия

Электронные конфигурации (в приближении независимого движения электронов):
основное состояние 1s2: S=0, терм 1S, мультиплетность 2S+1=1,
возбужденные состояния 1s2s:
S=1, терм 3S, мультиплетность 2S+1=3 (ортогелий),
S=0, терм 1S, мультиплетность 2S+1=1 (парагелий).
Энергия ортогелия меньше энергии парагелия (вследствие обменного взаимодействия).
Орто- (от др.-греч. ορθός «прямой») и пара- (παρα- «против», «возле», «мимо»)
3S 1S
75

76. Литература

1.
2.
3.
Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и
ядерная физика: учеб. пособие– М.: Физматлит, 2002
Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М.: Наука. 1971.
Давыдов А.С. Квантовая механика. − М.: Наука. 1971.
76