Похожие презентации:
Призма. Виды призмы. Свойства призмы
1. Многогранник, поверхность которого состоит из двух равных многоугольников расположенных в параллельных плоскостях, и n
параллелограммов называется призмой.Параллелограммы A1 B1 B2 A2 называются боковыми гранями
призмы, многоугольники A1A2A3 …An– ее основаниями,
отрезки A1B1, A2B2,, …Аn Вn называются боковыми ребрами
призмы.
.
2.
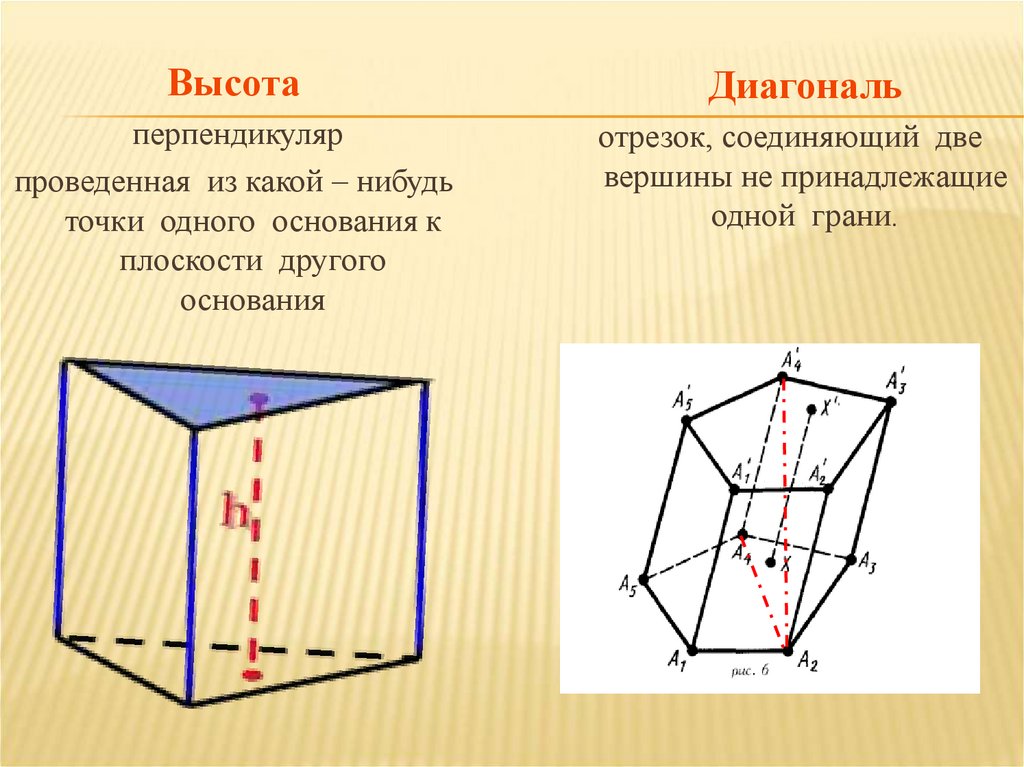
ВысотаДиагональ
перпендикуляр
проведенная из какой – нибудь
точки одного основания к
плоскости другого
основания
отрезок, соединяющий две
вершины не принадлежащие
одной грани.
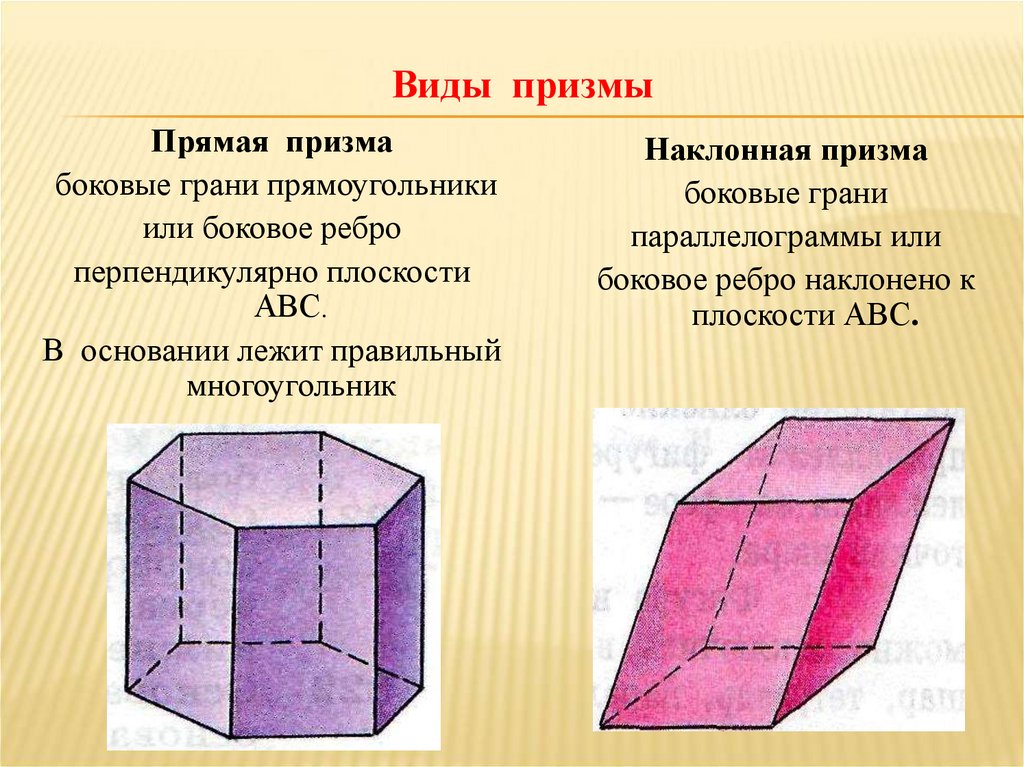
3. Виды призмы
Прямая призмабоковые грани прямоугольники
или боковое ребро
перпендикулярно плоскости
АВС.
В основании лежит правильный
многоугольник
Наклонная призма
боковые грани
параллелограммы или
боковое ребро наклонено к
плоскости АВС.
4. Свойства призмы.
1. Основания призмы являются равными многоугольниками.2. Боковые грани призмы являются параллелограммами.
3. Боковые ребра призмы равны.
4. Противоположные ребра параллельны и равны.
5. Все боковые ребра равны и параллельны.
6. Противоположные боковые грани равны и параллельны.
7. Высота перпендикулярна каждому основанию.
8. Диагонали пересекаются в одной точке и делятся в ней
пополам.
5. Нахождение площади
Площадь боковой поверхности прямой призмы равнапроизведению периметра основания на высоту призмы.
Sбок = Pосн · h
P - периметр
h – высота призмы
Площадь полной поверхности призмы называется сумма
площадей всех ее граней.
Sпол = Sбок + 2S осн
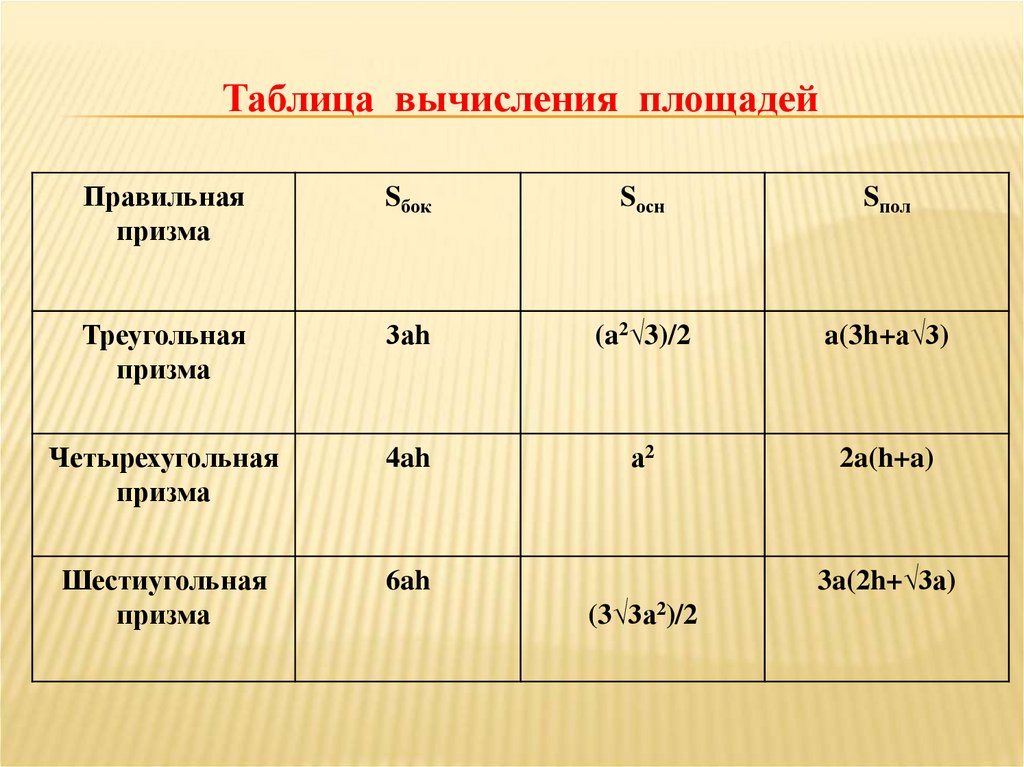
6. Таблица вычисления площадей
Правильнаяпризма
Sбок
Sосн
Sпол
Треугольная
призма
3аh
(a2√3)/2
a(3h+a√3)
Четырехугольная
призма
4ah
а2
2a(h+a)
Шестиугольная
призма
6ah
3a(2h+√3a)
(3√3а2)/2




 Математика
Математика








