Плотность вероятности

1.

Срез знаний
1 вариант
1)Какая
случайная величина называется
дискретной?
2) Как определяется сумма случайных
величин?
3) Вероятность сдачи экзамена первым
студентом равна 0,6, а вторым – 0,9.
Составить ряд распределения с.в. Х –
числа студентов, успешно сдавших экзамен
в случае, когда:
а) экзамены пересдавать нельзя;
б) экзамен можно один раз пересдать.
2 вариант
1) Что называют законом распределения
дискретной случайной величины?
2) Как определяется произведение случайной
величины на число?
3) Два стрелка делают по одному выстрелу в
мишень. Вероятность попадания для
первого стрелка равна 0,6, а для второго –
0,8. Найти и построить функцию
распределения с.в. Х – числа попаданий в
мишень.
3 вариант
1) Основное свойство закона распределения.
2) Что
называется
многоугольником
распределения?
3) Монета бросается 4 раза. Построить
многоугольник распределения с.в. Х – числа
выпадений герба.
4 вариант
1)
2)
3)
Как определяется произведение случайных
величин?
Приведите пример дискретной случайной
величины.
Убедиться, что функция
если x 0,
0,
F ( x)
x
1 e , если x 0
Является функцией распределения некоторой
случайной величины. Найти P{0 x 1}
и построить график F(x).

2.

Непрерывные случайные величины имеют
бесконечное число возможных значений.
Поэтому ввести для них ряд распределения
нельзя.
Вместо вероятности того, что случайная
величина Х примет значение, равное х, т.е.
p(X=x), рассматривают вероятность того, что Х
примет значение, меньшее, чем х, т.е. Р(Х<х), то
есть для непрерывной СВ можно задать
функцию распределения.

3.

Если СВ Х непрерывна, то вероятность того,
что она примет конкретное значение, равное
С, равна нулю: Р(Х=С)=0
Из того, что событие Х=С имеет нулевую
вероятность еще не следует, что это событие
невозможно.
Частота появления события в большой серии
опытов не равна, а только приближается к
вероятности данного события.
Поэтому если вероятность события равна 0, то
при неограниченном повторении опыта это
событие будет появляться сколь угодно
редко.

4.

Рассмотрим непрерывную случайную величину Х с функцией
распределения F(x).
Вычислим вероятность попадания этой случайной величины на
промежуток
[ x; x x)
p{x X x x} F ( x x) F ( x)
F ( x x) F ( x)
x
представляет собой среднюю вероятность, которая приходится
на единицу длины участка [ x; x x) т.е. среднюю
Отношение
плотность распределения вероятности.
Рассмотрим предел
F ( x x) F ( x)
lim
x 0
x
=

5.

По определению производной этот предел
равен производной функции F(x) :
=
F ( x) f ( x)
Функция f(x), равная производной
от функции распределения, называется
плотностью вероятности случайной
величины Х или плотностью
распределения.

6.

Кривая, изображающая плотность
называется кривой распределения.
вероятности,
Плотность вероятности является характеристикой
только непрерывных случайных величин.
P{x X x x}
Из того, что
f ( x) lim
x
p{x X x x} f ( x) x.
x 0
следует, что
Рассмотрим
вероятность
попадания
случайной
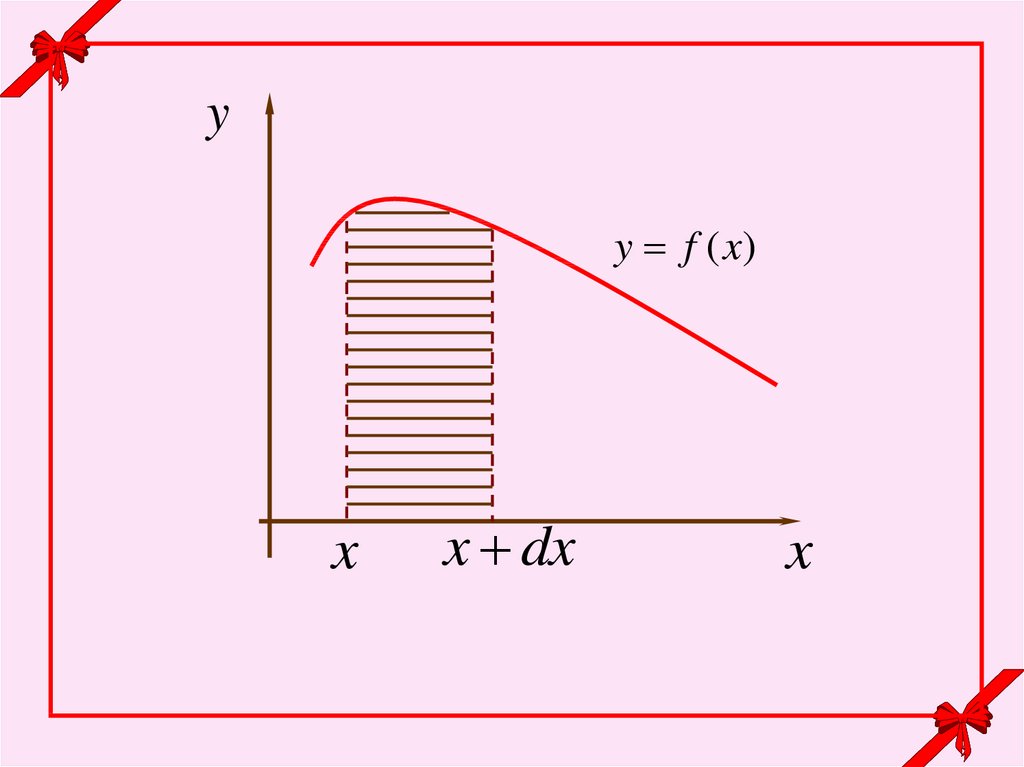
величины Х на элементарный участок dx: f(x)dx.
p{x X x dx} f ( x) dx.
Эта величина называется элементом вероятности и
геометрически означает площадь элементарного
прямоугольника со сторонами f(x) и dx:

7.

y
y f (x)
x
x dx
x

8.

Выразим вероятность попадания на
участок α до β через f(x). Она равна
сумме элементов вероятности на этом
участке, т.е. интегралу:
p( X ) f ( x)dx

9.

Отсюда
можно
распределения
вероятности:
выразить
через
функцию
плотность
x
F ( x) p( X x) p( X x)
f ( x)dx

10.

1
Плотность вероятности является
неотрицательной функцией
(т.к. функция распределения является
неубывающей функцией):
f x F x 0.
Это означает, что график плотности f(x), называемый кривой
распределения, не ниже оси абсцисс.
Плотность может принимать сколько угодно большие значения.

11.

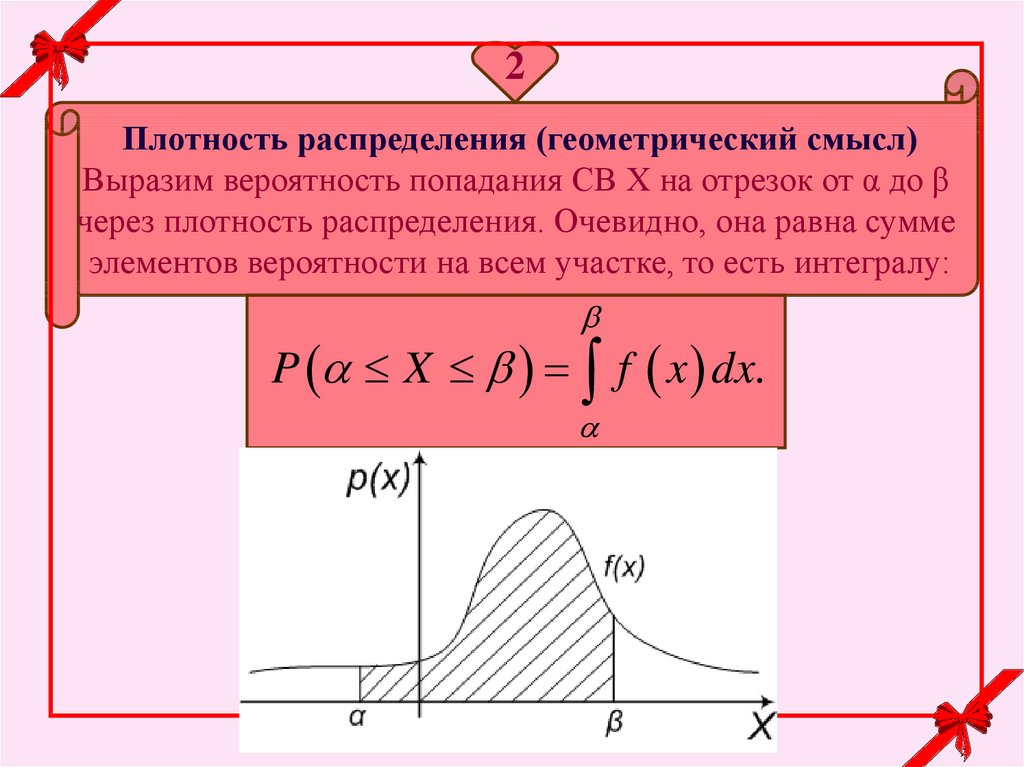
2
Плотность распределения (геометрический смысл)
Выразим вероятность попадания СВ X на отрезок от α до β
через плотность распределения. Очевидно, она равна сумме
элементов вероятности на всем участке, то есть интегралу:
P X f x dx.

12.

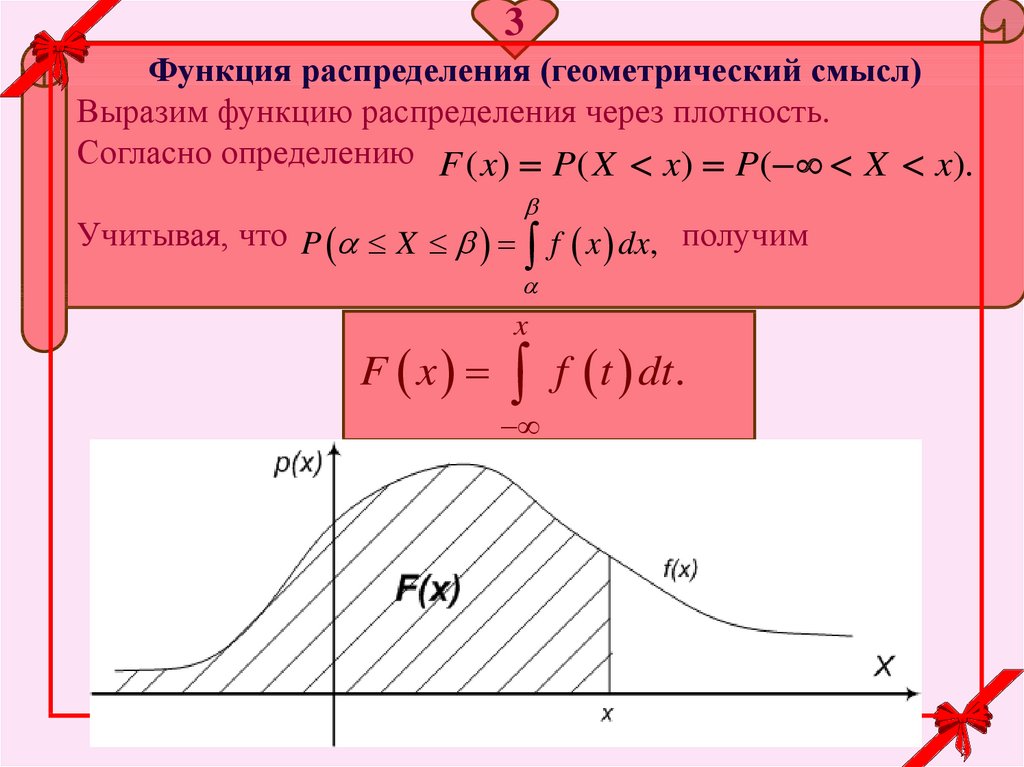
3
Функция распределения (геометрический смысл)
Выразим функцию распределения через плотность.
Согласно определению F ( x) P( X x) P( X x).
Учитывая, что P X f x dx, получим
F x
x
f t dt.

13.

4
Интеграл в бесконечных пределах
от плотности вероятности равен 1:
f ( x ) dx 1
f x dx F F 1.
Это означает, что площадь фигуры под кривой
распределения на бесконечных промежутках
интегрирования равна 1.

14.

Можно дать такое определение случайной величины:
Случайная величина Х называется непрерывной,
если существует неотрицательная функция f(x)
такая, что при любом х функцию распределения
можно представить в виде
x
F ( x)
f (t )dt.
А затем получить F ( x) f ( x).
Отсюда следует, что F ( x) и f ( x) являются
эквивалентными обобщающими характеристиками
с.в. Х.

15.

Докажем, что вероятность события {X=с}, где с – число,
для н.с.в., равна нулю.
Действительно,
c
P{ X c} p{c X c} f ( x)dx 0.
c
Отсюда следует, что
P{a X b} P{a X b} P{a X b} P{a X b}.

16.

ПРИМЕР
Плотность распределения с.в. Х задана функцией
a
f ( x)
.
2
1 x
Найти значение параметра a.

17.

РЕШЕНИЕ
a
Согласно свойству 4˚ плотности, имеем
dx 1,
2
1 x
d
т.е.
dx
a lim
1,
2
d 1 x
c c
т.е.
a lim arctgx c 1
d
d
c
1 и, наконец, получаем a 1,
2 2
или a
т.е.
a
1
.

18.

УПРАЖНЕНИЯ
1. Случайная величина Х задана функцией распределения:
при
x 1,
0,
F ( X ) a ( x 1) 2 , при 1 x 2,
1,
при
x 2.
Найти значение a, построить графики F(x) и f(x).
2. Кривая распределения н.с.в. Х имеет вид, указанный на рисунке.

19.

https://www.youtube.com/watch?v=mjhk2GhGy7s