Похожие презентации:
Непрерывная случайная величина. Функция распределения. Плотность вероятности. Урок № 21
1. Непрерывная случайная величина. Функция распределения. Плотность вероятности
Урок № 212. Основные вопросы темы
Способы задания случайных величинИнтегральная функция распределения
Плотность распределения
3.
Случайные величиныНепрерывные случайные
величины
Дискретные случайные
величины
4. Дать понятие дискретной случайной величины
Случайная величина, которая принимаетизолированные значения, называется
дискретной случайной величиной.
Число её значений – счетное.
Множество значений дискретной
случайной величины может быть как
конечным так и бесконечным.
5. Дать понятие непрерывной случайной величины
Случайная величина, которая принимаетсвои значения из некоторого конечного
или бесконечного интервала называется
непрерывной случайной величиной.
Число значений непрерывной случайной
величины всегда бесконечно.
6. Определить вид случайной величины
Ошибка при практических измеренияхОценка студента за экзамен по теории
вероятностей
Время бесперебойной подачи
электроэнергии на предприятии
Число израсходованных патронов
Количество израсходованного бензина на
поездку
7. Способы задания дискретной случайной величины
Задать значения случайной величины X:x1, x2, x3, x4, …
Указать вероятности значений случайной
величины X:
P(X = x1), P(X = x2), P(X = x3), …
8. Закон распределения дискретной случайной величины
Соотношение между возможнымизначениями случайной величины и их
вероятностями называется законом
распределения дискретной случайной
величины.
9. Способы задания ДСВ
Законраспределения
P X x1 p1 ,
P X x2 p 2 ,
........................
P X xn p n
10. Ряд распределения случайной величины
Таблица соответствия значений случайнойвеличины и их вероятностей называется рядом
распределения.
xi
pi
x1
p1
x2
p2
….
….
xn
pn
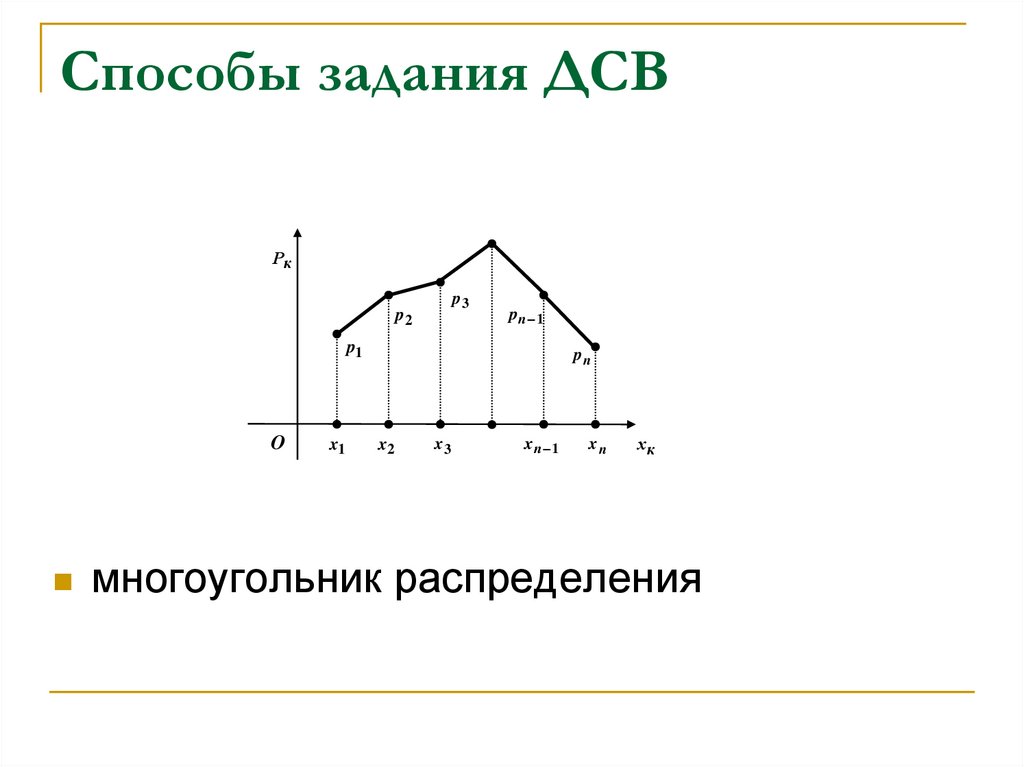
11. Способы задания ДСВ
Ркp3
p2
pn 1
p1
O
x1
pn
x2
x3
x n 1
xn
хк
многоугольник распределения
12. Способы задания ДСВ
Закон распределенияИнтегральная
функция
Ряд распределения
формула
Многоугольник
распределения
график
13. Интегральная функция распределения
Пустьx — действительное число.
Вероятность события, состоящего в том,
что X примет значение меньшее x, т. е.
вероятность события X < x обозначим
через F(x).
Разумеется, если x будет изменяться, то,
вообще говоря, будет изменяться и F(x),
т. е. F(x) есть функция от x.
14. Определение
Интегральной функцией распределенияназывают функцию F(x), определяющую
для каждого значения x вероятность того,
что случайная величина X примет
значение, меньшее x, т. е.
F x P X x
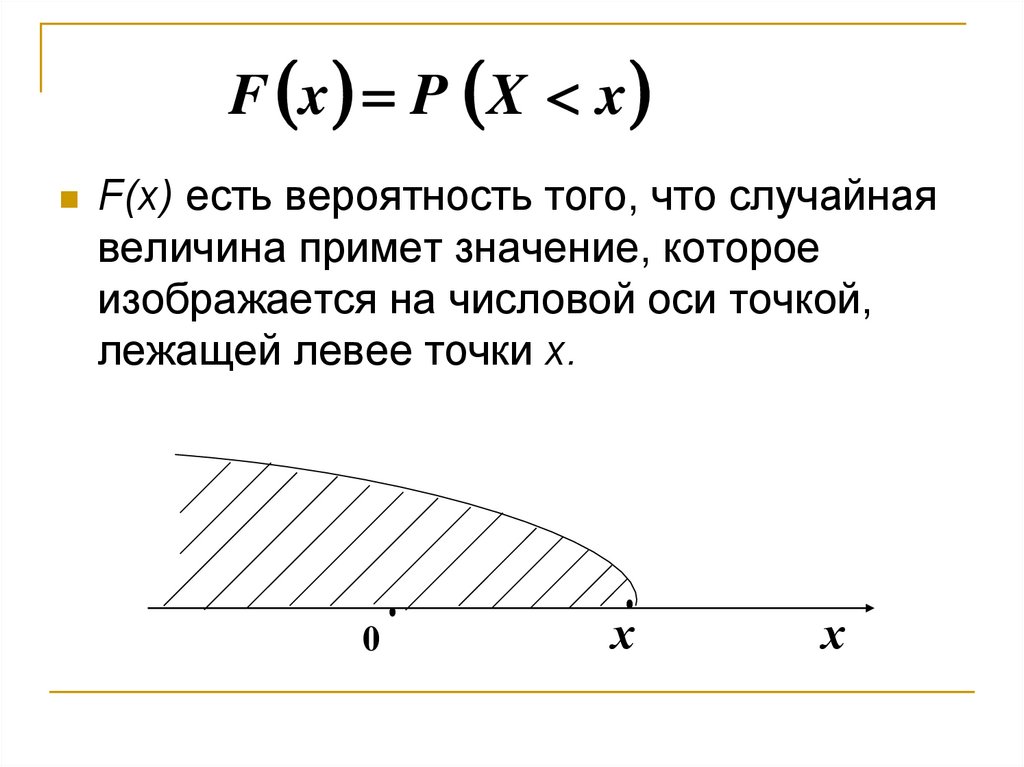
15.
F x P X xF(x) есть вероятность того, что случайная
величина примет значение, которое
изображается на числовой оси точкой,
лежащей левее точки x.
0
х
х
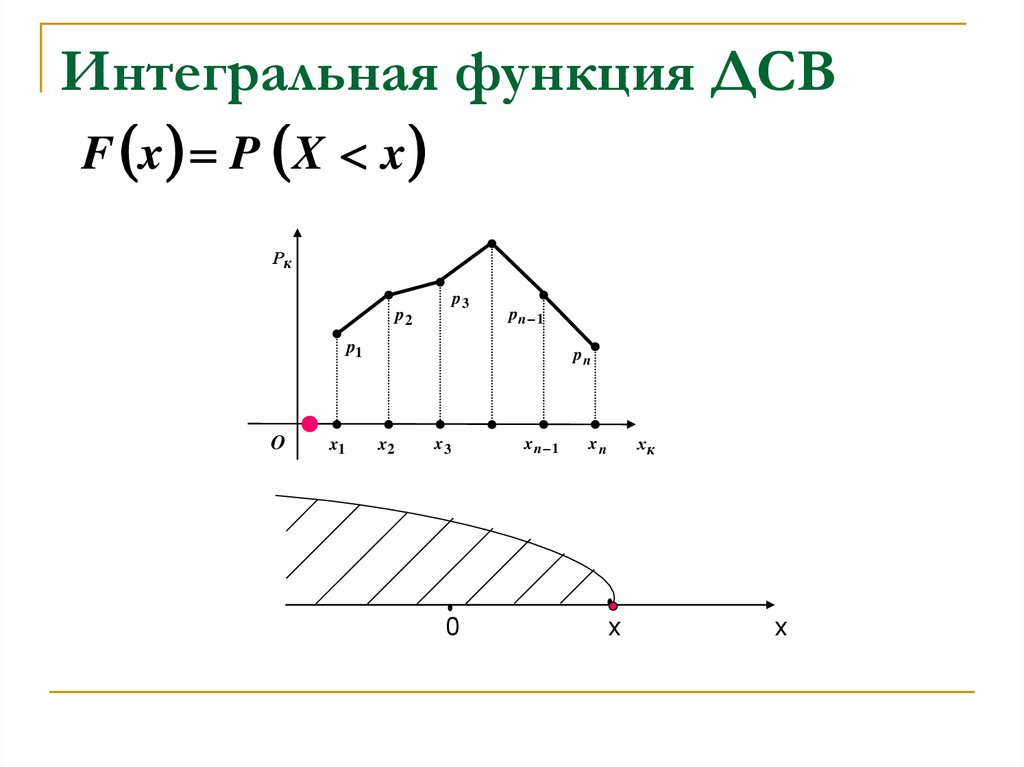
16. Интегральная функция ДСВ
F x P X xРк
p3
p2
pn 1
p1
O
x1
pn
x2
x3
0
x n 1
хк
xn
x
x
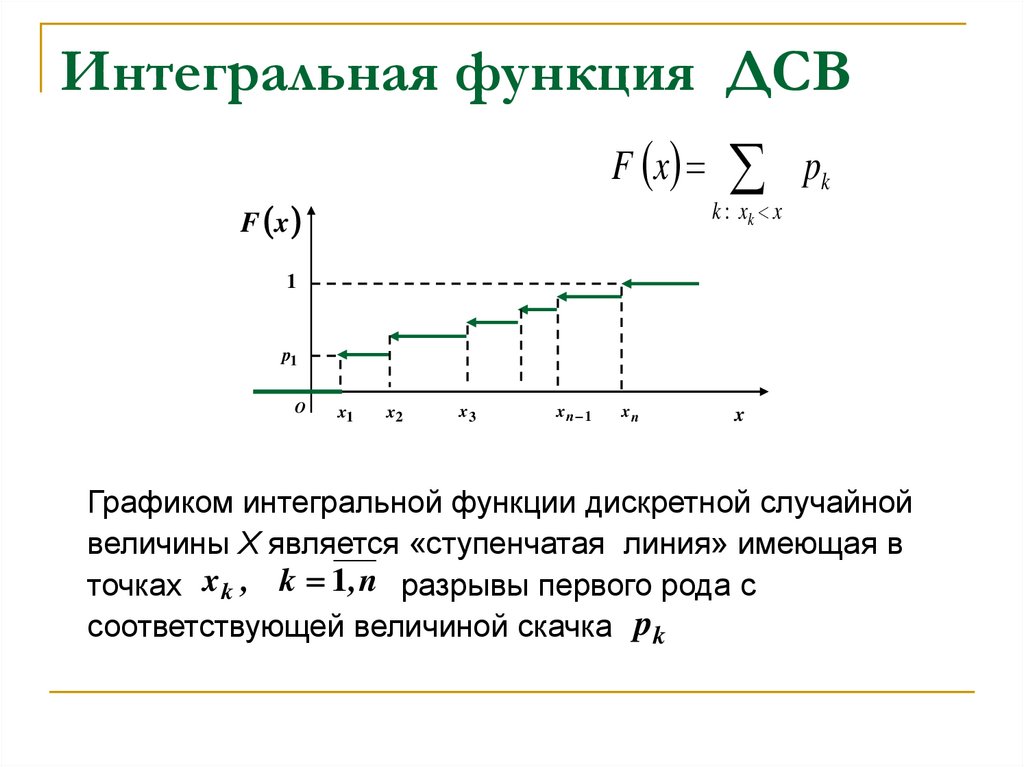
17. Интегральная функция ДСВ
F x pkF x
k : xk x
1
p1
O
x1
x2
x3
x n 1
xn
x
Графиком интегральной функции дискретной случайной
величины X является «ступенчатая линия» имеющая в
точках x k , k 1 , n разрывы первого рода с
соответствующей величиной скачка pk
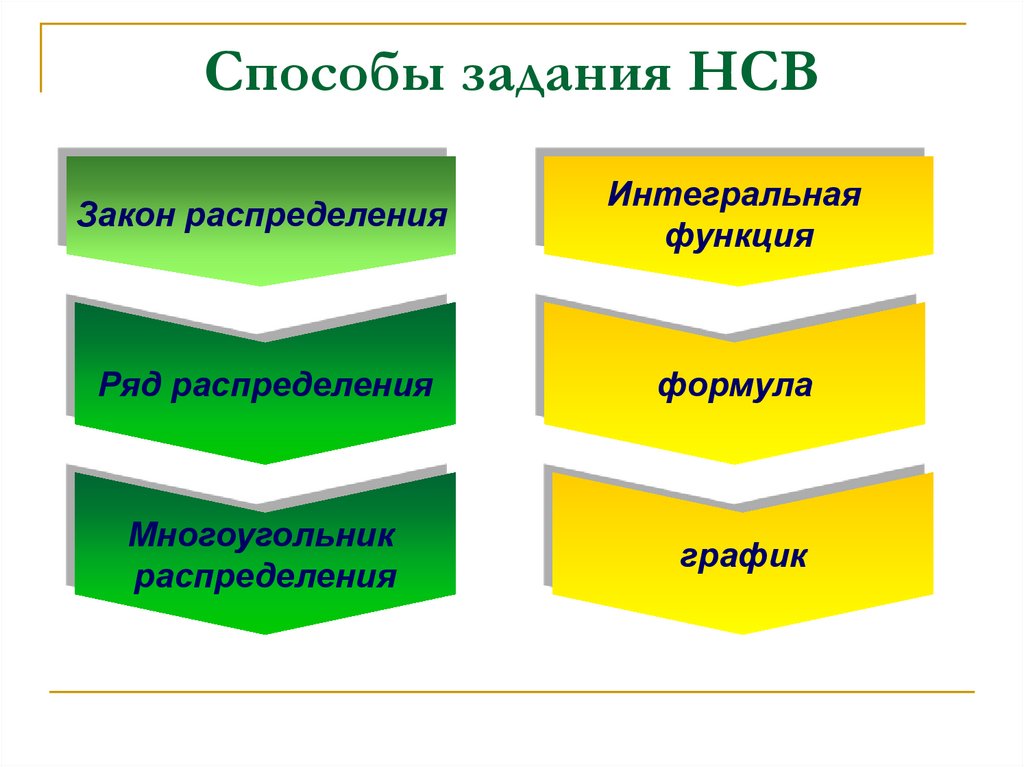
18. Способы задания НСВ
Закон распределенияИнтегральная
функция
Ряд распределения
формула
Многоугольник
распределения
график
19. Свойства интегральной функции распределения
Значения интегральной функциипринадлежат отрезку [0, 1]: т.е.
0 F x 1
что следует из определения интегральной
функции как вероятности, а вероятность –
всегда есть неотрицательное число, не
превышающее единицы.
20. Свойства интегральной функции распределения
Интегральная функция– неубывающая
функция, т.е. при х1 x 2 F x1 F x 2
Следствие 1. Вероятность того, что
случайная величина примет значение,
заключенное в интервале (a, b), равна
приращению интегральной функции на
этом интервале, т.е. P a X b F b F a
21. Свойства интегральной функции распределения
Если возможные значения случайнойвеличины принадлежат интервалу (a, b), то
1) F x 0 при x a 2) F x 1 при x b
Следствие 2. Если возможные значения
непрерывной случайной величины
расположены на всей оси , то справедливы
следующие предельные соотношения:
lim F x 0; lim F x 1.
x
x
22. Свойства интегральной функции распределения
Вероятность того, что непрерывнаяслучайная величина примет одно
определенное значение, равна нулю.
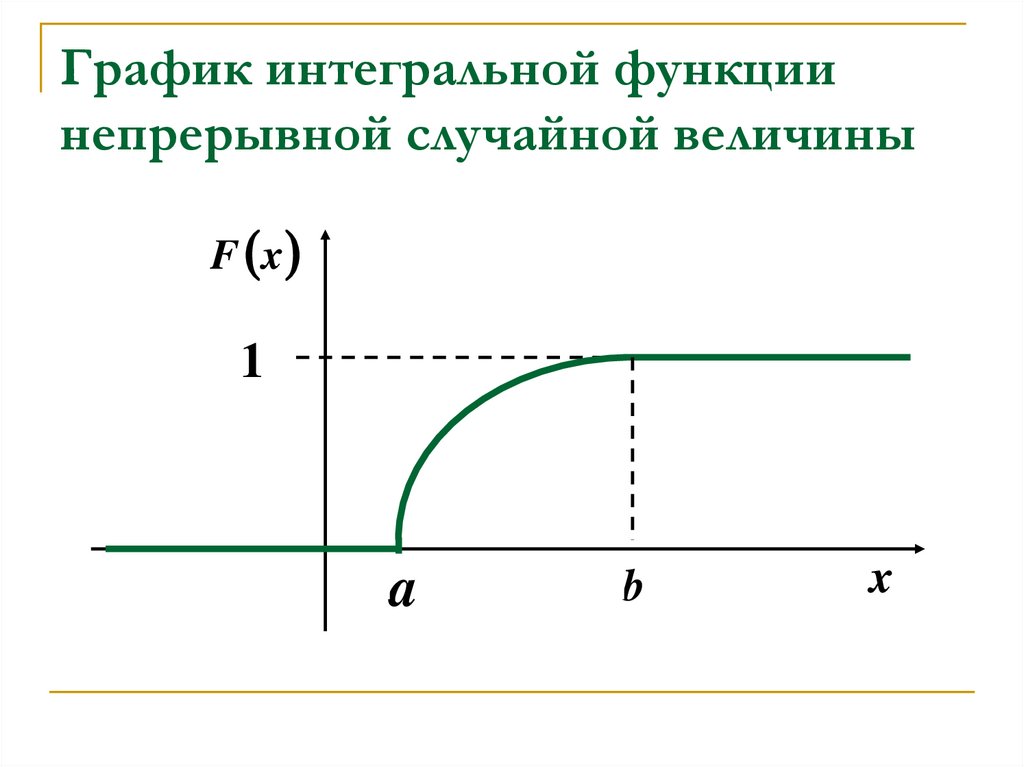
23. График интегральной функции непрерывной случайной величины
F x1
a
b
x
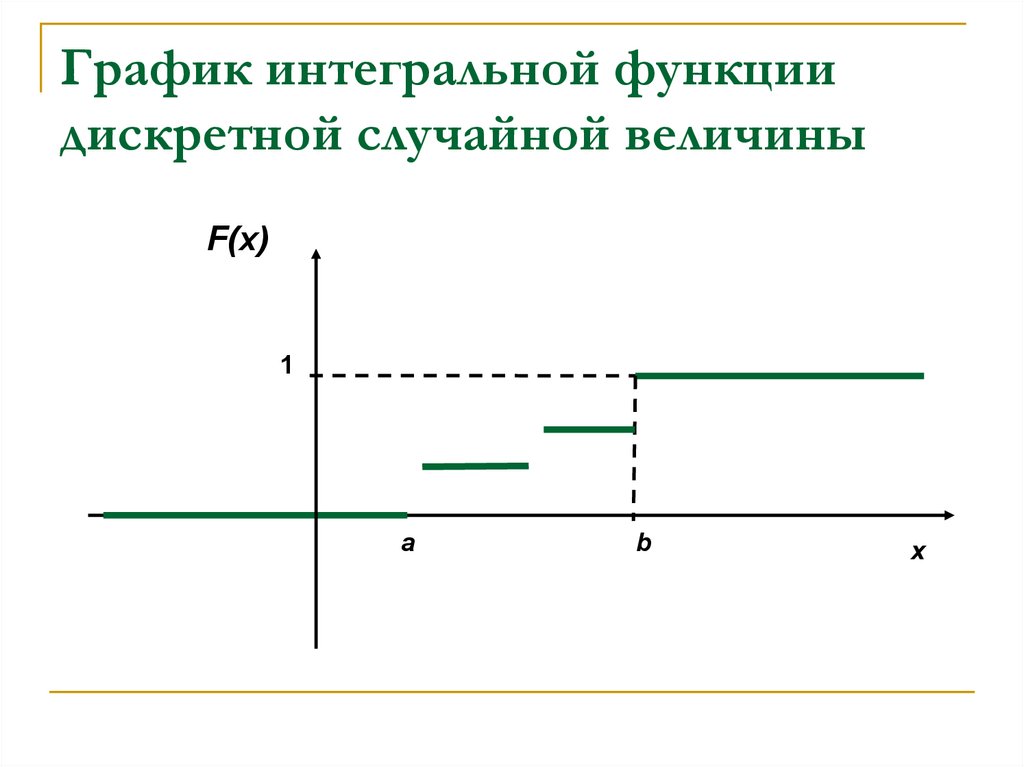
24. График интегральной функции дискретной случайной величины
F(x)1
a
b
x
25. Дифференциальная функция распределения и ее свойства
Дифференциальной функциейраспределения вероятностей или
плотностью распределения называется
первая производная интегральной
функции распределения непрерывной
случайной величины, т.е.
f x F x
26. Плотность распределения
F x x F x P x X x xf x F x lim
x 0
x
x
При малом
x функция имеет смысл
плотности вероятности, т.к. она равна
отношению вероятности попадания
случайной величины внутрь интервала
x , x x к длине этого интервала.
27. Плотность распределения
Вероятность того, что непрерывнаяслучайная величина примет значения,
принадлежащие интервалу (а, b), равна
определенному интегралу на этом
промежутке от ее дифференциальной
функции распределения, т.е.
b
P a X b f x dx
a
28. Доказательство
bb
a
a
P a X b F b F a F x dx f x dx
т.е. вероятность попадания в интервал
(а, b), равна площади криволинейной
трапеции, ограниченной сверху
дифференциальной функцией
распределения.
29. Свойства дифференциальной функции распределения
f x 0 – неотрицательная.Действительно, т.к.
F x – неубывающая
функция, то ее производная
положительна, следовательно, и
F x f x 0
30. Свойства дифференциальной функции распределения
f x dx 1Действительно, т.к. событие
– X
достоверное, то
f x dx P X 1
31. Свойства дифференциальной функции распределения
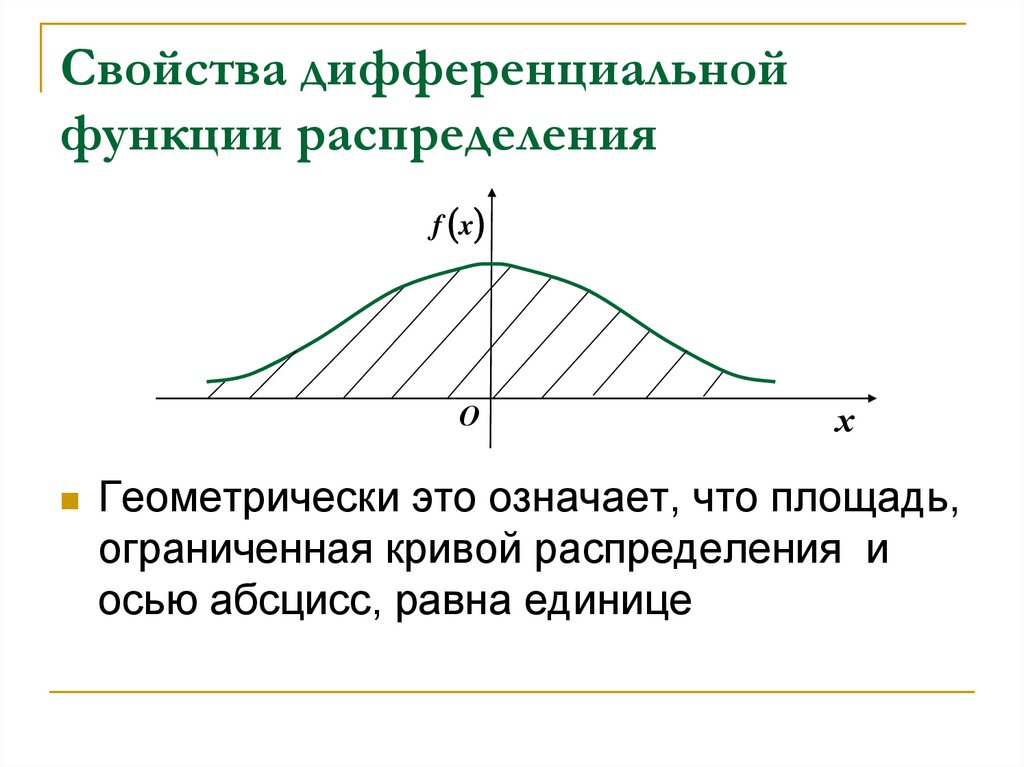
f xО
х
Геометрически это означает, что площадь,
ограниченная кривой распределения и
осью абсцисс, равна единице
32. Свойства дифференциальной функции распределения
Если все возможные значениянепрерывной случайной величины
заполняют промежуток (a, b), то
b
f
x
dx
1
a
33. Свойства дифференциальной функции распределения
Связь между интегральной идифференциальной функциями
распределения:
если известна интегральная функция, то
F x f x
если известна дифференциальная
x
функция, то
F x f x dx
34. Свойства дифференциальной функции распределения
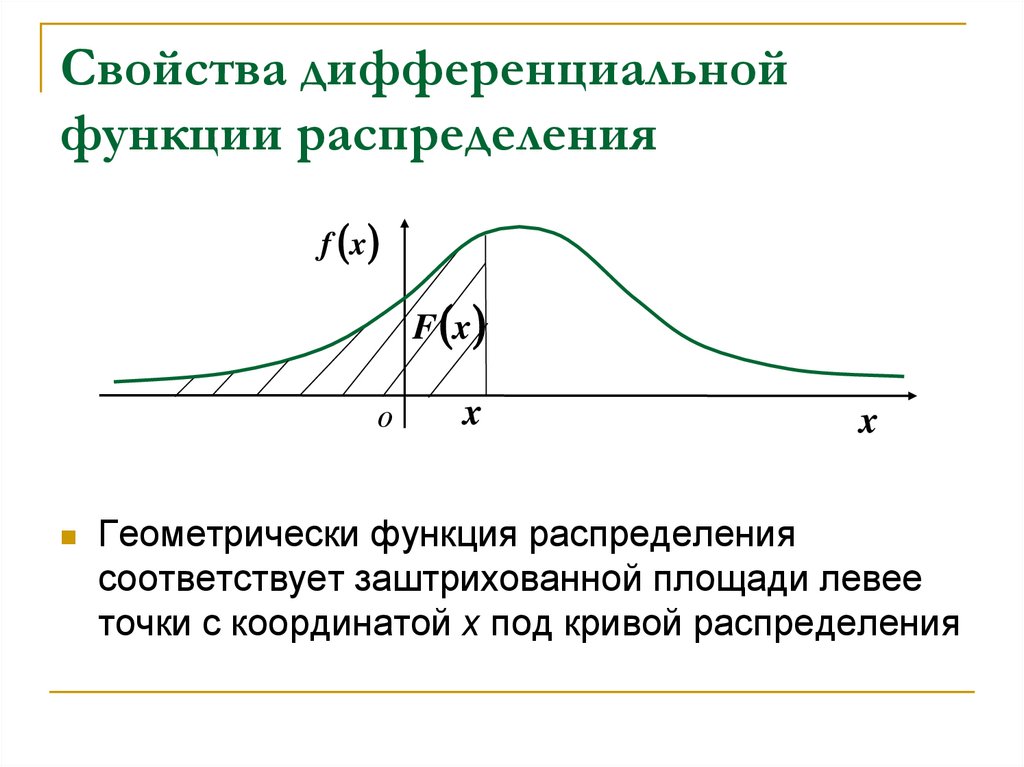
f xF x
О
x
x
Геометрически функция распределения
соответствует заштрихованной площади левее
точки с координатой x под кривой распределения
35. Типы случайных величин?
Дискретнаяслучайная
величина
Непрерывная
случайная
величина
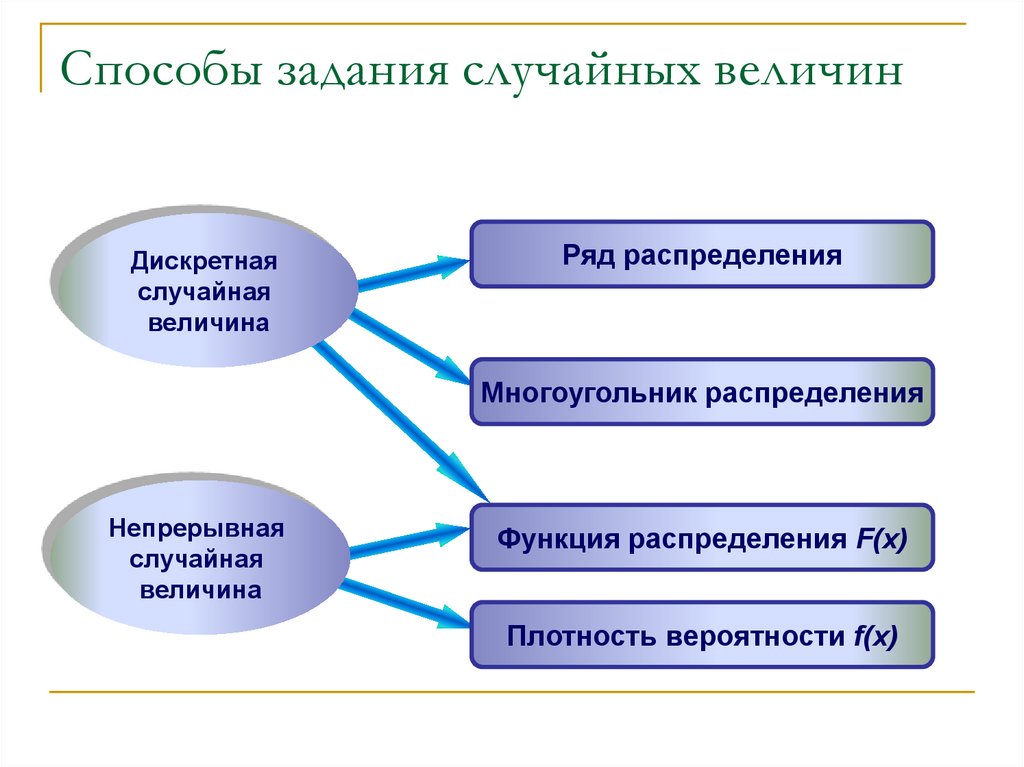
36. Способы задания случайных величин
Дискретнаяслучайная
величина
Ряд распределения
Многоугольник распределения
Непрерывная
случайная
величина
Функция распределения F(x)
Плотность вероятности f(x)
37. Вопросы к теме
1. Можно ли задать непрерывнуюслучайную величину рядом
распределения? Обоснуйте ответ.
2. Вероятность невозможного события
равна нулю. Верно ли обратное
утверждение: если вероятность равна
нулю то событие - невозможное?
38. Вопросы к теме
3. Можно ли задать дискретную случайнуювеличину дифференциальной функцией
распределения? Обоснуйте ответ.
4. В чем заключается связь между
дифференциальной и интегральной
функциями распределения?
5. Какой способ является универсальным
для задания дискретной и непрерывной
случайной величины?
39. Задание 1
Дана дискретная случайная величина X.P(X = -1) = 0,3
P(X = 2) = 0,5
P(X = 4) = 0,2
Задать ее:
рядом распределения,
многоугольником распределения,
интегральной функцией
40. Задание 2
Непрерывная случайная величина заданаинтегральной функцией распределения.
Построить ее график.
Найти P(1< X < 3)
Найти дифференциальную функцию, построить
ее график.
0; x 0
x
F ( x) ; 0 x 2
2
1; x 2
41. Задание 3
Непрерывная случайная величина заданадифференциальной функцией распределения.
Построить ее график.
Найти P(1,5 < X < 3)
Найти интегральную функцию, построить ее
график.
0; x 1
f ( x) 3
x 4 ; x 1
42. Самостоятельно
Непрерывная случайная величина заданаинтегральной функцией распределения.
Построить ее график.
Найти P(1< X < 2)
Найти дифференциальную функцию, построить
ее график.
0; x 0
2
x
F ( x) ; 0 x 2
4
1; x 2
43. Домашнее задание
Калинина § 5.3 стр. 69, задача № 5.2, 5.3Калинина § 5.4 стр. 77, задача № 5.4, 5.5






























 Математика
Математика








