Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления

1.

Выполнила Котомина О.В.
учитель математики
высшей категории
Санкт-Петербург

2. Цилиндр Материал предназначен для учащихся 11класса - определение цилиндра, - развёртка цилиндра, - формулы для вычисления

площади основания,
площади боковой поверхности,
площади полной поверхности цилиндра,
- решение задач,
- задания для самопроверки

3. Этапы урока

Теория
«Пошаговое» решение задачи
Практическая работа по группам
Сечение цилиндра
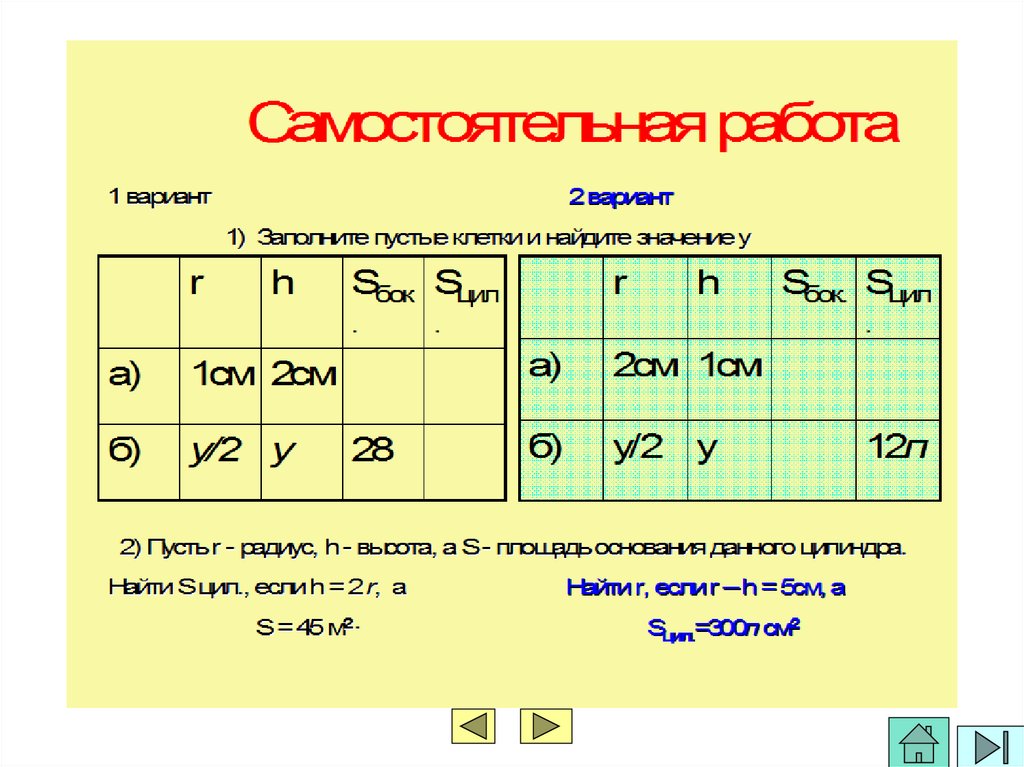
Самостоятельная работа
Слабо? Докажи!

4.

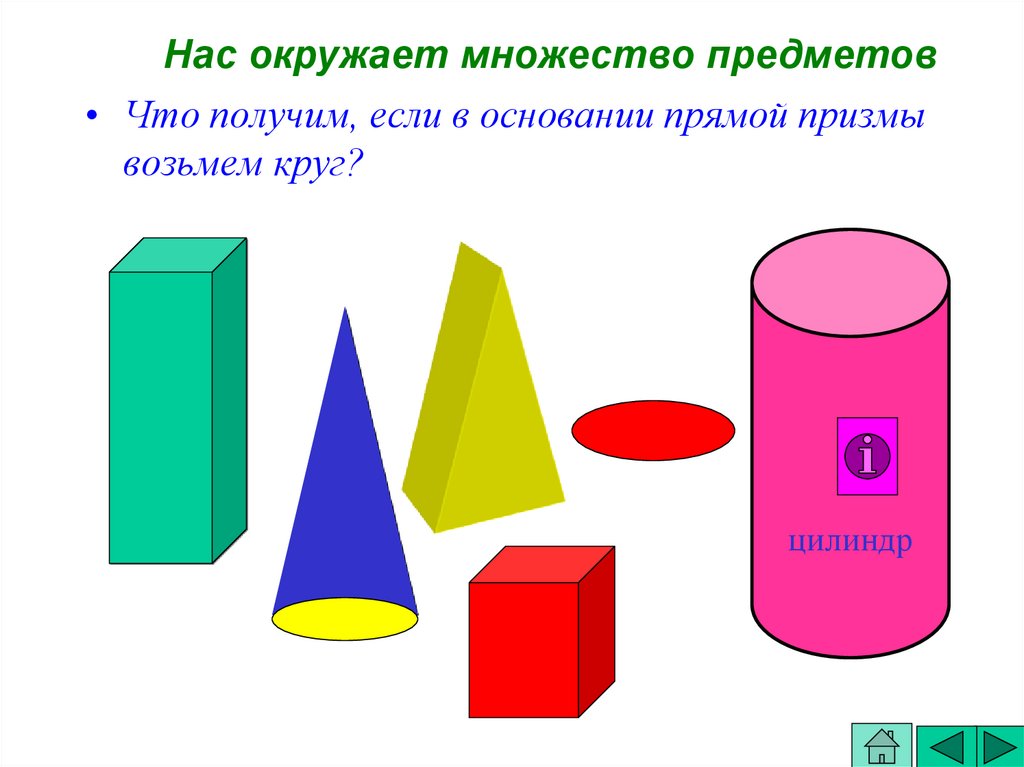
5. Нас окружает множество предметов

• Они отличаются формой, размерами, материалом, из
которого изготовлены, окраской. Разных людей
интересуют разные качества этих предметов.
Математиков интересуют форма предметов и их
размеры. Поэтому вместо предметов они
рассматривают геометрические тела: куб, призма,
пирамида, цилиндр, конус, шар и т.д.
• Названия многих геометрических тел идут из
глубокой древности, причем произошли они от
соответствующих предметов.
Например, из Древней Греции пришёл термин
«цилиндр» (килиндрос - валик).

6.

Нас окружает множество предметов
• Что получим, если в основании прямой призмы
возьмем круг?
цилиндр

7. Что такое цилиндр?

L
L1
Цилиндр – это
тело, ограниченное
цилиндрической
поверхностью и
двумя кругами с
границами (LиL1)

8. Как называется отрезок, соединяющий точки окружностей оснований, перпендикулярный плоскостям оснований?

Образующая цилиндра
Все образующие параллельны оси
вращения и имеют одинаковую
длину, равную высоте цилиндра.
Чему будет равна высота
цилиндра,
если длина образующей
цилиндра 5 см?
5 см

9. Сделайте чертёж цилиндра.

• Проведите 2 образующие.
• Выделите верхнее основание.
• Проведите ось вращения.

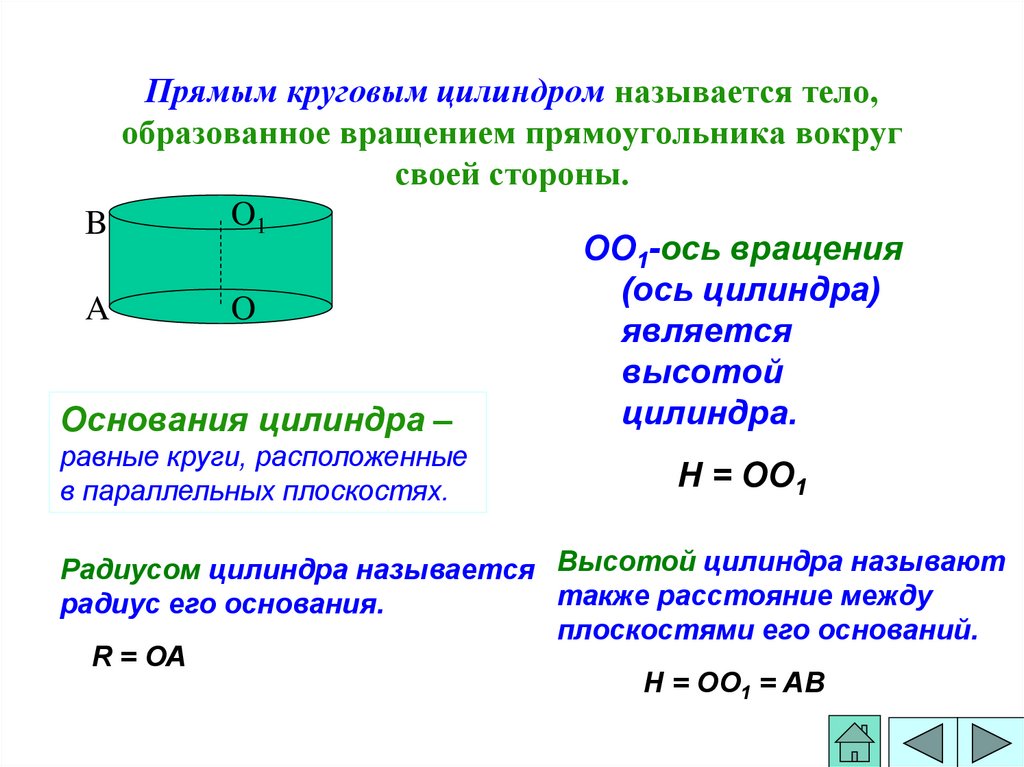
10. Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг своей стороны.

O1
B
ОО1-ось вращения
(ось цилиндра)
A
O
является
высотой
цилиндра.
Основания цилиндра –
равные круги, расположенные
в параллельных плоскостях.
H = ОО1
Радиусом цилиндра называется Высотой цилиндра называют
также расстояние между
радиус его основания.
плоскостями его оснований.
R = ОА
Н = ОО1 = АВ

11. Так выглядит развертка цилиндра. Разверткой боковой поверхности цилиндра является прямоугольник со сторонами Н и С, где Н –

высота цилиндра,
С- длина окружности основания.
Формулы
для вычисления площади боковой
поверхности и площади
полной поверхности цилиндра.
Н
С= r
Sбок.= НС = 2 RН
Sосн.= R2,
Sп.п.ц. =Sбок.+2Sосн.=
= R (R+Н)

12. Решим задачу

• Диагональ развёртки боковой
поверхности цилиндра
составляет угол 30о с
основанием развертки, длина
этой диагонали равна 4 см.
Найти площадь полной
поверхности цилиндра.
4см
300

13.

• 1шаг.Разверткой боковой поверхности является
прямоугольник АА1В1В.
Из прямоугольного треугольника АА1В
A
находим
АА1 = А1В*sin30о = 4 *1/2
=2 см = Н,
АВ =А1В*сos30о = 4 * 3 =
2
2 3 см = С = R
A1
B
B1

14.

• 2шаг. из последнего
следует, что
R = 2 3 см
23 3
R
см
2
3шаг. Далее имеем
Sп.п.= R(R + H) =
3
3 6
3
2
2
2
3
2
4
3
Ответ:
6
4 3см2

15. Практическая работа

• Оборудование.
• Раздаточный материал для
• 1и 3 группы прямоугольник (со сторонами 16х20 см),
• 2группа квадрат( со стороной 15 см ),
• 4группа прямоугольник (со сторонами 12х16 см)

16.

Задание для 1 группы
• Цилиндр получается вращением прямоугольника
вокруг меньшей его стороны. Вычислить площадь
полной поверхности, получившегося цилиндра.
С
В
Д
А
Дано: цилиндр, АВСDпрямоугольник,
Н=АВ=16см, R=АD=20см
Найти: Sп.п.
Решение:
Sп.п. = 2 R(R + Н)=
= 2 20(20+16)=
= 40 *36=1440 см2
Ответ: 1440 см2

17. Задание для 2группы

Цилиндр получается вращением квадрата вокруг его
стороны. Вычислите площадь полной поверхности,
получившегося цилиндра.
С
Д
В
А
Дано: цилиндр, АВСD-прямоугольник
R=АВ= 16 см,
Н=АD= 20 см
Найти: Sп.п.
Решение:
Sп.п. = R(R+Н) = 2 *16(20+16) =
= 32 *36 = 1152 см2
Ответ: 1152 см2

18.

Задание для 3 группы
• Цилиндр получается вращением прямоугольника
вокруг большей его стороны. Вычислите
площадь полной поверхности, получившегося
цилиндра.
С
Д
В
А
Дано: цилиндр, АВСDпрямоугольник
R=АВ= 16 см,
Н=АD= 20 см
Найти: Sп.п.
Решение:
Sпп= R(R+Н) =
2 *16(20+16) =
= 32 *36 = 1152 см2
Ответ: 1152 см2

19.

Задание для 4 группы
• Трубка, цилиндрической формы получается из
прямоугольника. Вычислите радиус основания
• Дано: цилиндры 1 и 2
прямоугольник 12 х16см
1
2
Найти: R1, R2
Решение:
С = R
C1= R =12, R1= С/2 =12/2 =6
C2 = R =16, R2=С/2 =16/2 =8
Ответ: R1=6 см, R2=8 cм

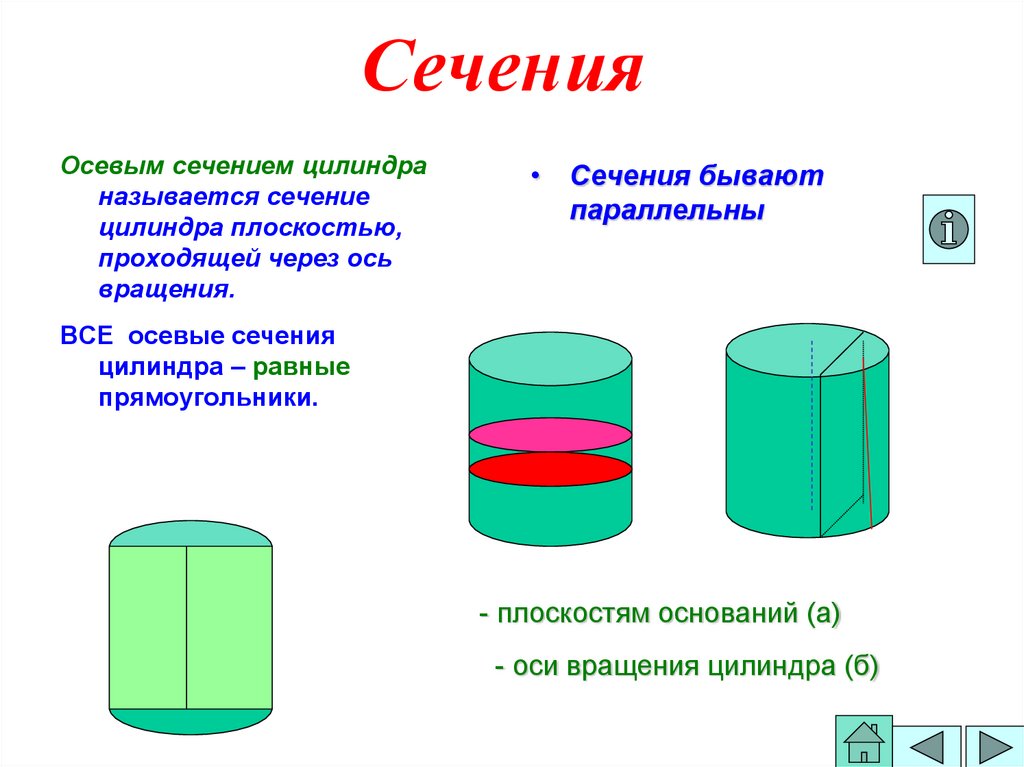
20. Сечения

Осевым сечением цилиндра
называется сечение
цилиндра плоскостью,
проходящей через ось
вращения.
• Сечения бывают
параллельны
ВСЕ осевые сечения
цилиндра – равные
прямоугольники.
- плоскостям оснований (а)
- оси вращения цилиндра (б)

21. Знай, что

- если плоскость сечения параллельна основаниям
цилиндра, то
это круг и он перпендикулярен его оси вращения.
- если плоскость параллельна оси вращения и
проходит на расстоянии от оси, меньшем радиуса
цилиндра, то
это будет прямоугольник и он перпендикулярен
основаниям.

22.

На практике нередко встречаются предметы,
которые имеютформу
более сложных
цилиндров.
образующая
Сечение не параллельно
основанию
парабола

23.

24. Сверь ответ 1вариант

1задание
а) Sбок.= 4П см2,
Sцил.= 6П см2
б) у = 28
П
Sцил.= 42
2задание
Sцил. = 270 м2

25. Сверь ответ 2вариант

1 задание
а) Sбок.= 4П см2,
Sцил.= 12П см2
б) у = 2 2
Sбок.= 8П
2 задание
h = 5см, r = 10 см

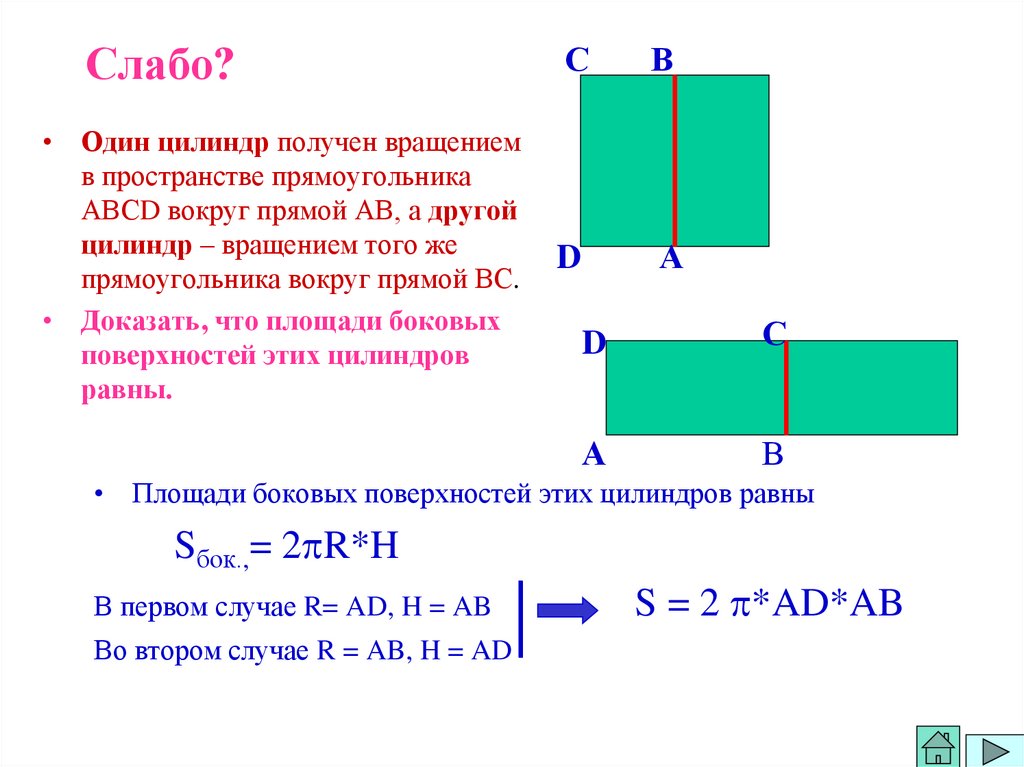
26. Слабо?

• Один цилиндр получен вращением
в пространстве прямоугольника
АВСD вокруг прямой АВ, а другой
цилиндр – вращением того же
прямоугольника вокруг прямой ВС.
• Доказать, что площади боковых
поверхностей этих цилиндров
равны.
С
В
D
А
D
С
А
В
• Площади боковых поверхностей этих цилиндров равны
Sбок.,= 2 R*H
В первом случае R= AD, H = AB
Во втором случае R = AB, H = AD
S = 2 *AD*AB

27. Подведем итог.

- Составьте 5 основных вопросов по теме
«Цилиндр».
- Какое тело получится при
вращении квадрата вокруг его
диагонали?
- Это тема следующих уроков.