Похожие презентации:
Понятие цилиндра
1. Учитель математики МБОУ «Усть-абаканская СОШ» Водянова Л.А.
2.
1.Как можно получить цилиндрЕсли в одной из 2
параллельных
плоскостей взять
окружность, и из каждой
ее точки восстановить
перпендикуляр до
пересечения со второй
плоскостью, то получится
тело, ограниченное
двумя кругами и
поверхностью,
образованной из
перпендикуляров, это
тело называется
Круги,
лежащие в параллельных
плоскостях, называются
цилиндром.
основаниями цилиндра, а
отрезки, соединяющие
соответствующие точки
окружностей оснований –
3.
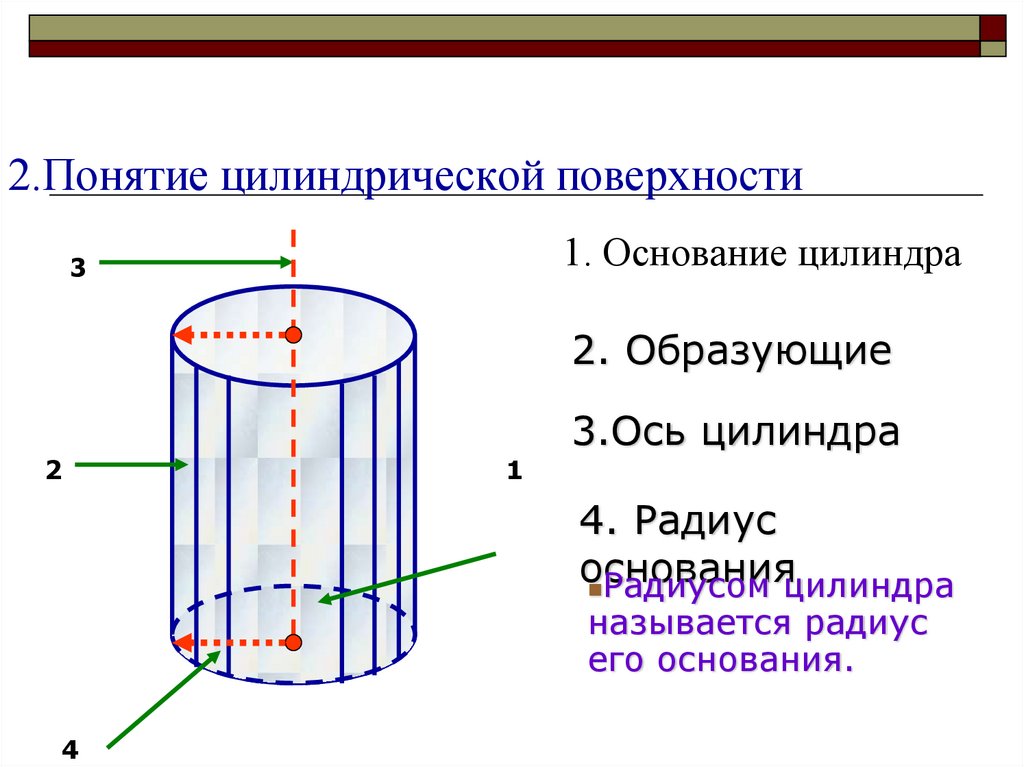
2.Понятие цилиндрической поверхности1. Основание цилиндра
3
4
2. Образующие
3.Ось цилиндра
2
1
4. Радиус
основания
Радиусом цилиндра
называется радиус
его основания.
4
4.
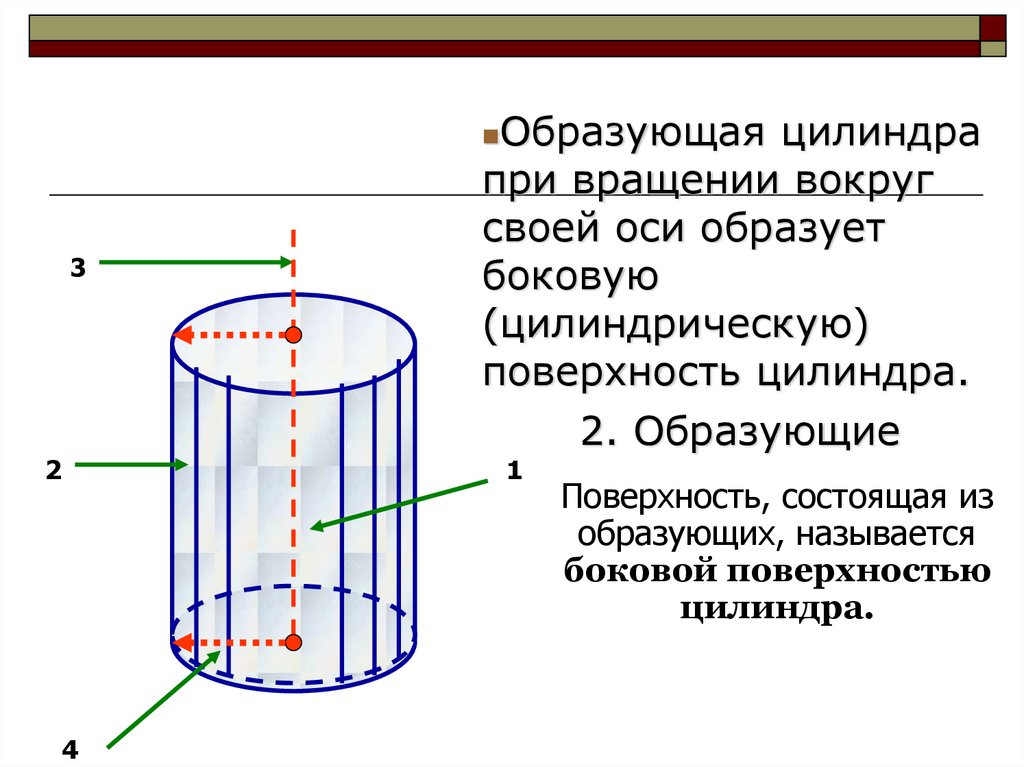
Образующая цилиндрапри вращении вокруг
своей оси образует
боковую
(цилиндрическую)
поверхность цилиндра.
2. Образующие
3
4
2
4
1
Поверхность, состоящая из
образующих, называется
боковой поверхностью
цилиндра.
5. Основные понятия
Образующая цилиндра – это отрезок,соединяющий соответствующие точки
окружностей кругов.
У цилиндра множество образующих.
6. Основные понятия
Радиус цилиндра – это радиус его основания.ОБОЗНАЧАЕТСЯ:
R
7. Основные понятия
Высота цилиндра – это расстояние междуплоскостями его оснований, т.е. отрезок
оси между центрами его оснований.
ОБОЗНАЧАЕТСЯ: H
Длина высоты прямого цилиндра равна длине
образующей
8.
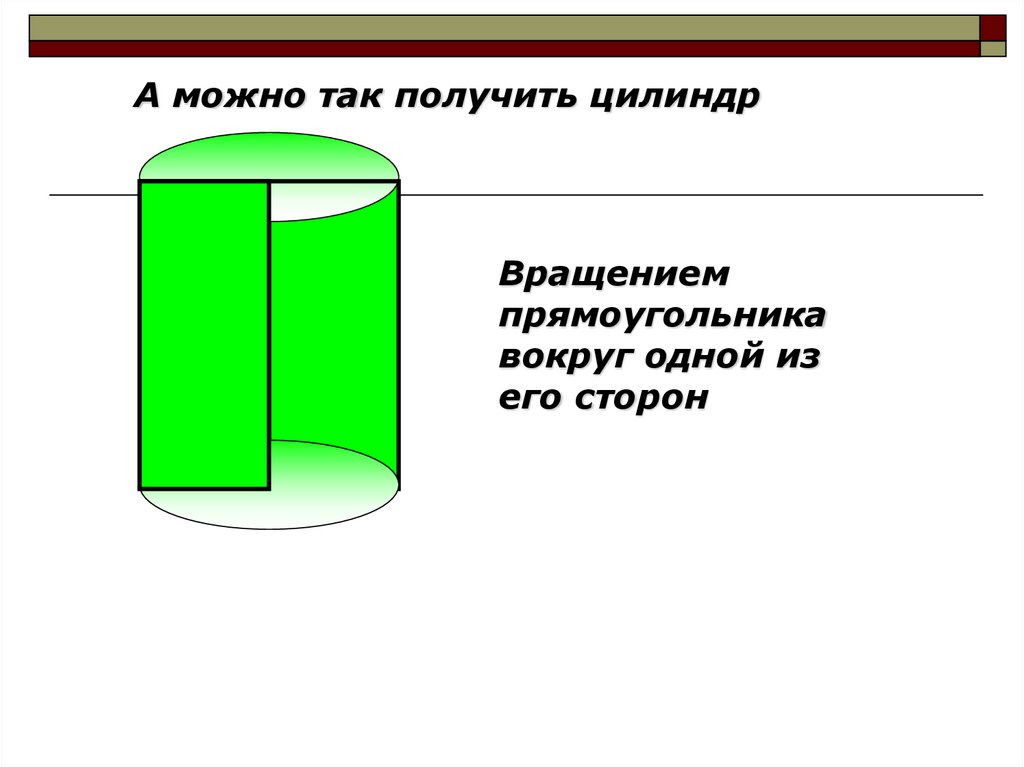
А можно так получить цилиндрВращением
прямоугольника
вокруг одной из
его сторон
9. Цилиндр – это тело, полученное вращением прямоугольника вокруг прямой, содержащей его сторону.
10.
Прямая, вокруг которой вращаетсяпрямоугольник называется осью цилиндра
11.
Прямой круговой цилиндроснование
О1
боковая
поверхность
образующая
О
ось цилиндра
12.
Наклонный круговой цилиндркруг
Н
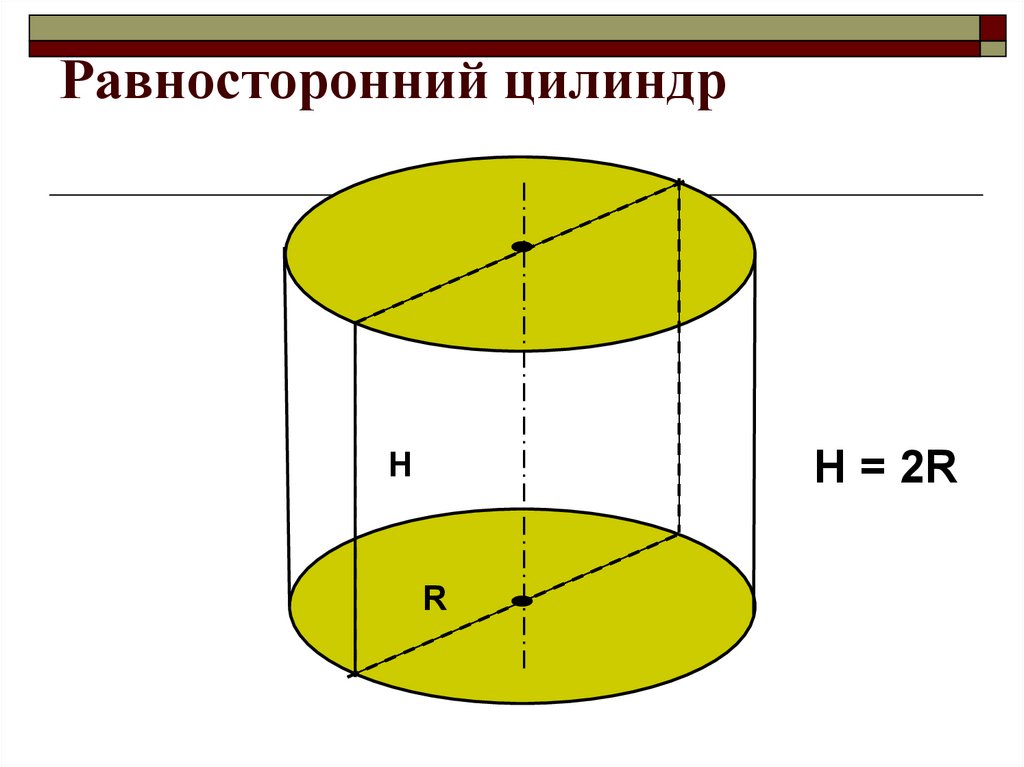
13. Равносторонний цилиндр
H = 2RH
R
14.
С 2 RR
О1
О1
H
So R
2
Sб 2 R H
О
S п 2 R H 2 R 2 R ( H R)
2
О
R
15.
16.
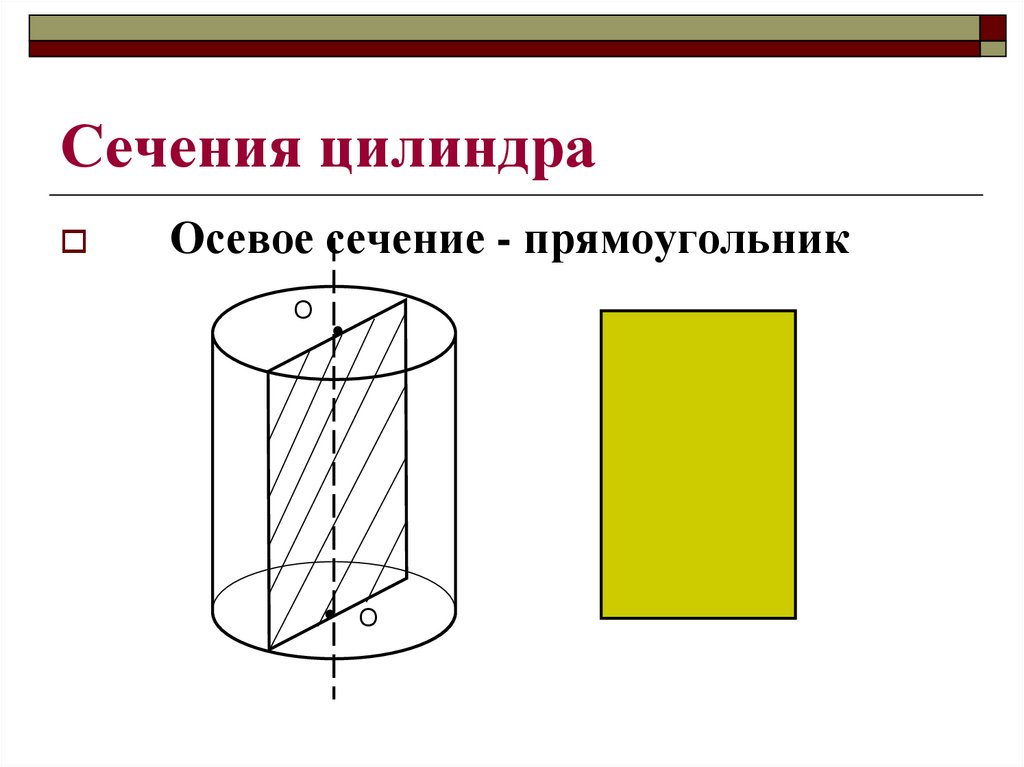
Если секущаяплоскость
проходит через ось
цилиндра, то сечение
является
прямоугольником.
Такое сечение носит
название осевого
сечения.
17. Сечения цилиндра
Осевое сечение - прямоугольникО
О
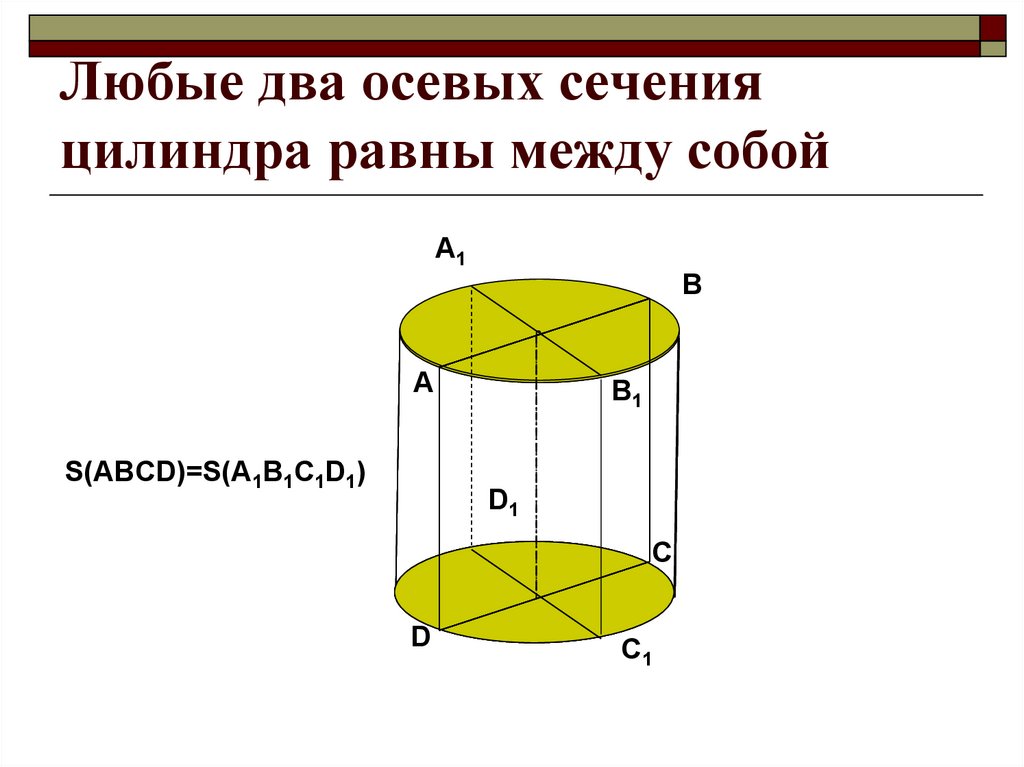
18. Любые два осевых сечения цилиндра равны между собой
A1B
A
S(ABCD)=S(A1B1C1D1)
B1
D1
C
D
C1
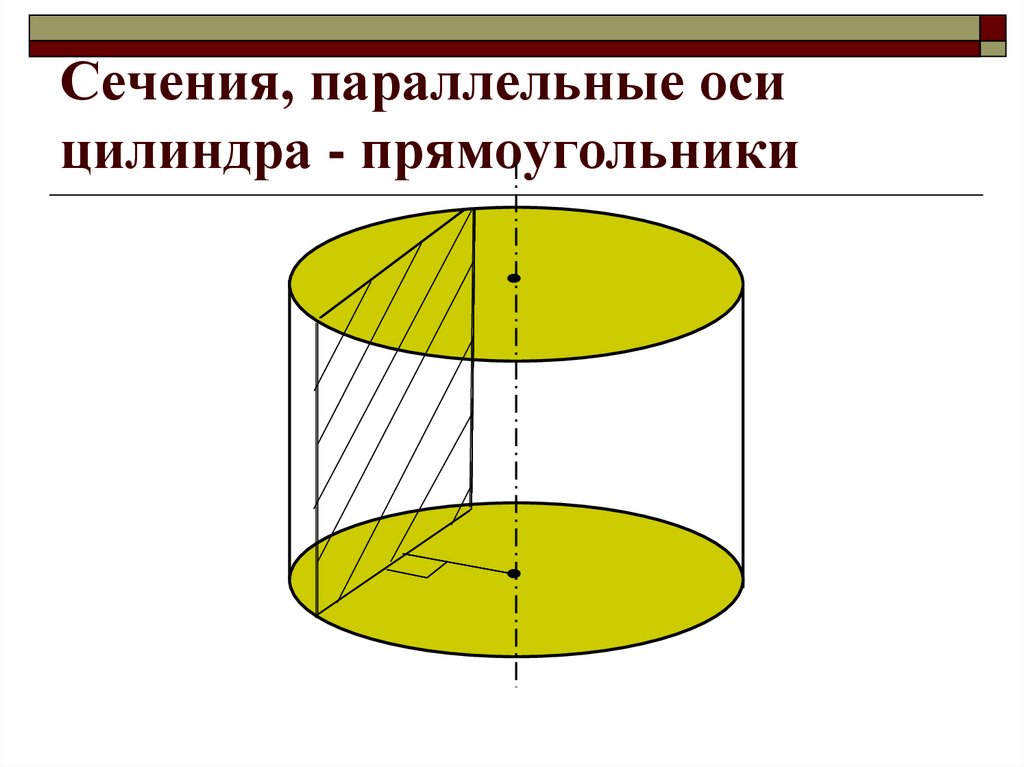
19. Сечения, параллельные оси цилиндра - прямоугольники
20.
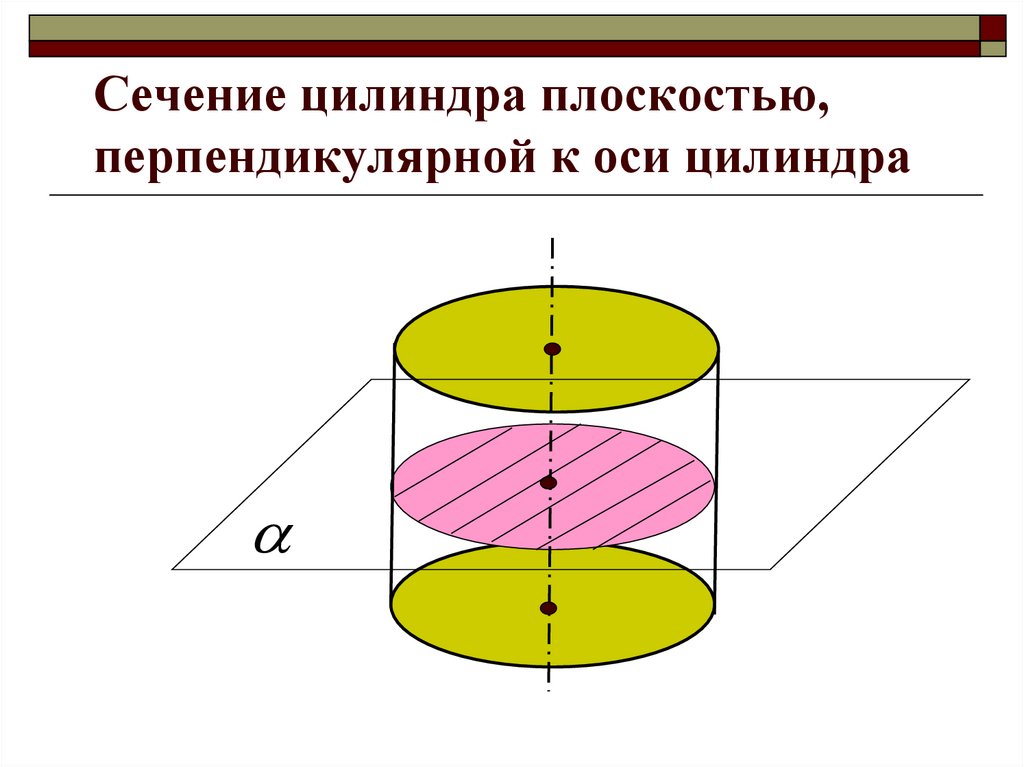
Если секущаяплоскость
перпендикулярна к
оси
цилиндра, то сечение
является кругом.
21. Сечение цилиндра плоскостью, перпендикулярной к оси цилиндра
22.
Сечение ,параллельное оси
цилиндрапрямоугольник
о1
Сечение плоскостью,
перпендикулярной к
оси или
параллельное
основаниям, является
кругом.
α
γ
β
о
Если сечение проходит через
ось цилиндра, то оно имеет
форму прямоугольника и
называется «осевым»
β
23. Сечение- Эллипс
Бывает и так24.
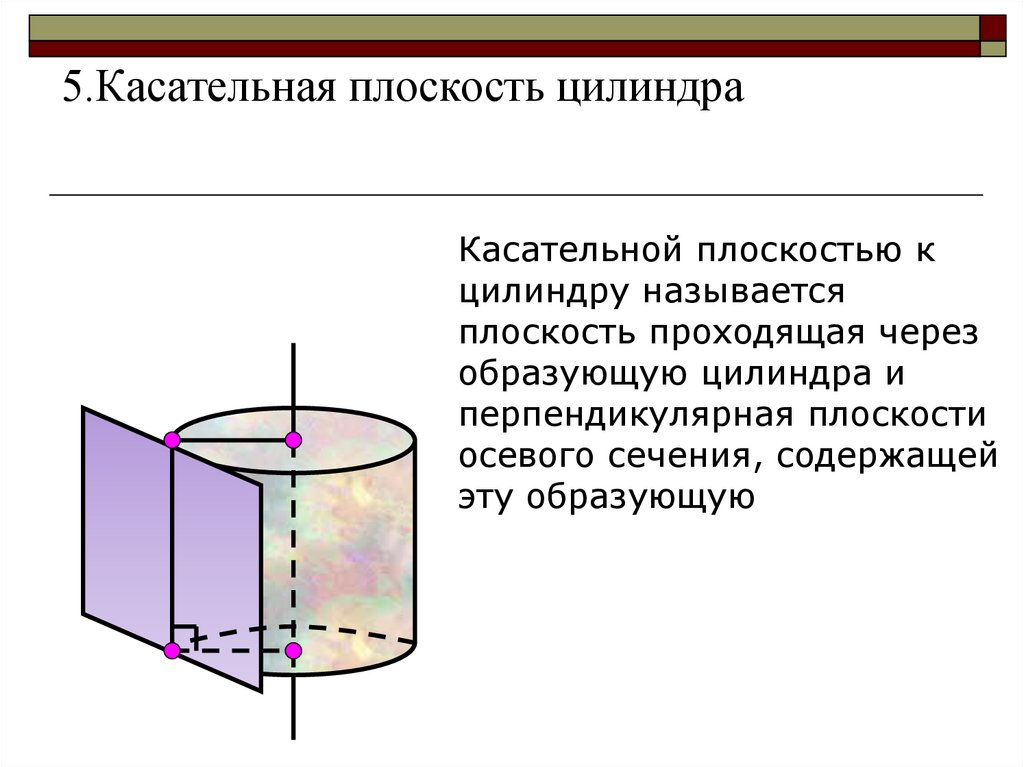
5.Касательная плоскость цилиндраКасательной плоскостью к
цилиндру называется
плоскость проходящая через
образующую цилиндра и
перпендикулярная плоскости
осевого сечения, содержащей
эту образующую
25.
26. Найти площадь полной поверхности цилиндра
В5
А
45º
r
С
АВС
- прямоугольный
АВС
- равнобедренный
ВС=АС=5
r=2,5
S=2πr(h+r)
S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5π
27.
№523Осевое сечение цилиндра – квадрат,
диагональ которого равна 20 см. Найдите:
а) высоту цилиндра; б) So цилиндра
Решение.
B
C
1. Проведем диагональ АС
сечения АВСD.
2. ADC – равнобедренный,
прямоугольный, АD=DC, h = 2r,
45
20
CAD = ACD=45 , тогда
2
h AC cos 45 20
10 2 .
2
3. Найдем радиус основания
45
A
D
4. Найдем площадь основания
Ответ: а )10 2 ;
б )50 .
h 10 2
r
5 2.
2
2
2
So r 5 2 50 .
2
28.
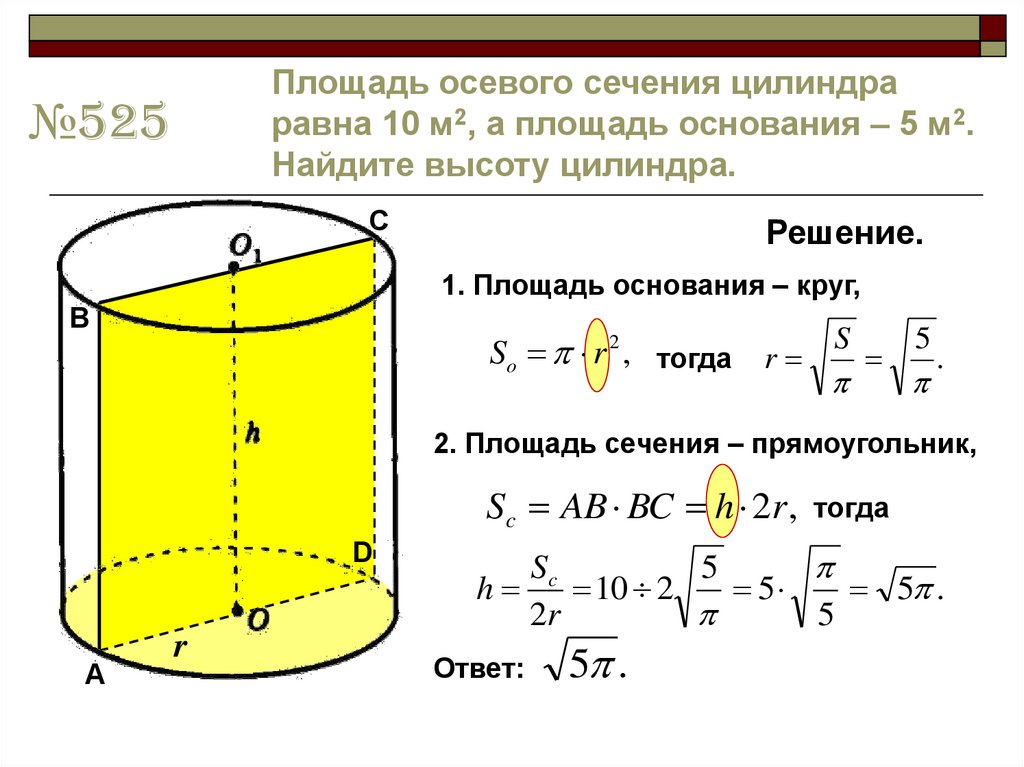
Площадь осевого сечения цилиндраравна 10 м2, а площадь основания – 5 м2.
Найдите высоту цилиндра.
№525
C
Решение.
1. Площадь основания – круг,
B
So r 2 , тогда r S 5 .
2. Площадь сечения – прямоугольник,
Sc AB BC h 2r ,
D
A
r
тогда
Sc
5
h
10 2
5
5 .
2r
5
Ответ:
5 .
29.
№527В
Концы отрезка АВ лежат на разных основаниях цилиндра.
Радиус цилиндра равен r, его высота – h, расстояние между
прямой АВ и осью цилиндра равно d. Найдите: a) высоту,
если r = 10, d = 8, AB = 13.
1. Построим отрезок АВ.
Решение.
2. Проведем радиус АО.
3. Построим отрезок d.
4. Отрезок ОК – искомое расстояние.
5. Из прямоугольного АОК находим:
a
AK r 2 d 2 100 64 6,
С
К
А
значит АС = 12.
6. Из прямоугольного АВС находим:
d r
ВС АВ 2 АС 2 169 144 5.
r
Итак, h = 5.
Ответ: 5.
30.
№529 Высота цилиндра равна 8 см, радиусравен 5 см. Найдите площадь сечения
цилиндра плоскостью, параллельной его оси,
если расстояние между этой плоскостью и
C
осью цилиндра
равно 3 см.
O1
B
ABCD- прямоугольник
SABCD= AB·AD, H=AB=8 см.
OK- расстояние от О до AD
H
K
R
A
D
OK AD, AK=KD, AK=4 см
AD=8 см
O
SABCD=8·8=64 (см2)
31.
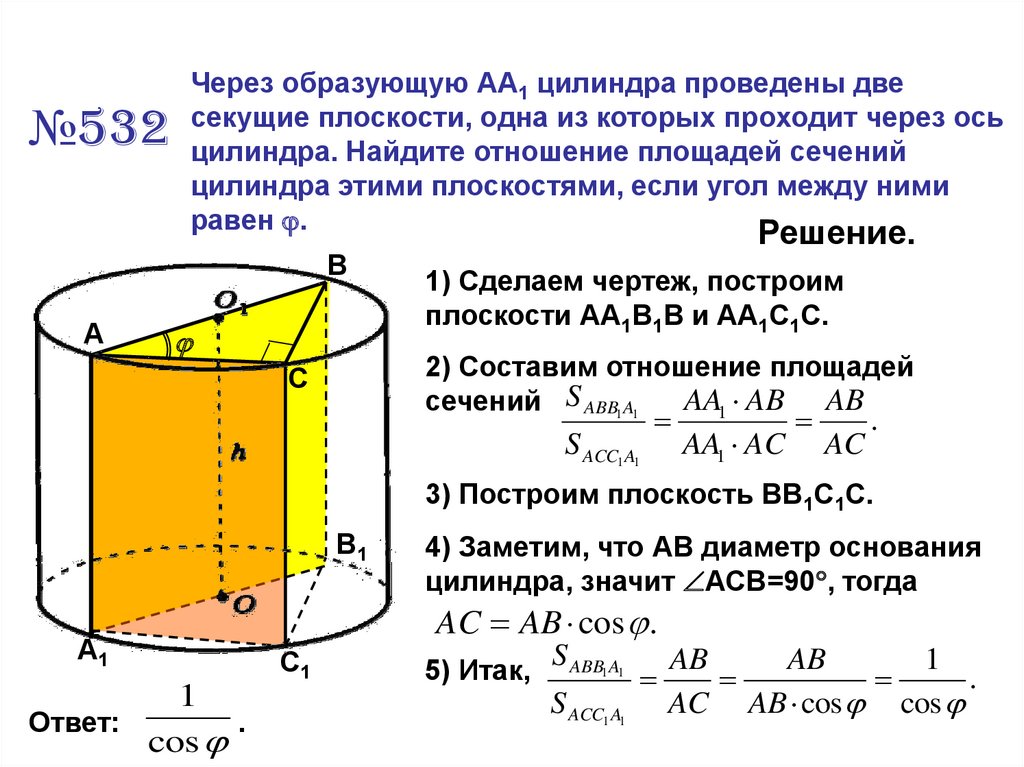
№532Через образующую АА1 цилиндра проведены две
секущие плоскости, одна из которых проходит через ось
цилиндра. Найдите отношение площадей сечений
цилиндра этими плоскостями, если угол между ними
равен .
Решение.
В
A
1) Сделаем чертеж, построим
плоскости АА1В1В и АА1С1С.
2) Составим отношение площадей
AA1 AB AB
сечений S ABB1 A1
C
S ACC1 A1
AA1 AC
AC
.
3) Построим плоскость ВВ1С1С.
В1
А1
1
Ответ:
.
cos
4) Заметим, что АВ диаметр основания
цилиндра, значит АСВ=90 , тогда
AC AB cos .
C1
5) Итак,
S ABB1 A1
S ACC1 A1
AB
AB
1
.
AC AB cos cos
32.
Реши задачуЗАДАЧА
Радиус основания цилиндра
равен 2м, высота 3м. Найдите
площадь осевого сечения.
Ответ: 12 м.кв.
33. ЗАДАЧА
Плоскость , параллельная осицилиндра, отсекает от окружности
основания дугу AmD с градусной
мерой . Радиус цилиндра равен a,
высота равна h, расстояние между
осью цилиндра ОО1 и плоскостью
равно d.
1) Докажите, что сечение
цилиндра плоскостью
есть прямоугольник.
1) Составьте план
вычисления площади
сечения по данным , h, d.
2) Найдите AD, если
a = 10 см, = 60 .
2) Найдите AD, если
a = 8 см, = 120 .
Ответ: 10
Ответ:
8 3
34.
Домашнее заданиеПовторить стр.130-132, гл. 1, п.59-60,
№530, № 537.























 Математика
Математика








