Множества и операции над ними

1. Множества и операции над ними

2.

«Множество есть
многое, мыслимое
нами как единое».
Основоположник
теории множеств,
немецкий математик
Георг Кантор
(1845-1918)

3.

Понятие множества принадлежит к числу основных,
неопределяемых понятий математики.
Множество – совокупность объектов, объединенных
по определенному признаку.
Примеры множеств:
- множество студентов в данной аудитории;
- множество людей, живущих на нашей планете в данный момент
времени;
- множество точек данной геометрической фигуры;
- множество чётных чисел;
- множество корней уравнения 5х+6=0.

4.

Назовите множества, изображенные на рисунках
Множество букв – это…
АЛФАВИТ
Множество кораблей – это…
ФЛОТ
Множество коров – это…
СТАДО
Множество деревьев – это…
ЛЕС

5. Объекты, составляющие данное множество, называют его элементами.

Множество обычно обозначают большими латинскими
буквами (A, B, C, …), а элементы множества − малыми
латинскими буквам (a, b, c, …).
Если элемент, а принадлежит множеству А, то пишут:
а ∈ А
Если а не принадлежит А, то пишут:
а ∉ А

6.

В математике часто исследуются так называемые числовые
множества, т.е. множества, элементами которых являются
числа.
Для самых основных числовых множеств
утвердились следующие обозначения:
N - множество всех натуральных чисел;
Z - множество всех целых чисел;
Q - множество всех рациональных чисел;
R - множество всех действительных чисел.

7.

Прочитать следующие высказывания
и указать среди них истинные:
100 N
8 Z
102 R
0 Z
2 Q
R
3 N
3
R
7
1
3 N
2
5 ,36 Q
4 , 3 Q
0 ,2531 Z

8. Поставьте вместо звездочки знак так, чтобы получить правильное утверждение: 1) 5 * N; 2) –5 * Q; 3) 3,14 * Q; 4) 2 * R; 5) 0 *

N; 6) − 12 * Z; 7) π * Q

9.

Слово «множество» используется для любого количества
элементов, то есть множество может содержать как
конечное, так и бесконечное число элементов.
Пример:
• Во множестве дней недели 7 элементов;
• Во множестве естественных спутников Земли 1 элемент;
• Во множестве целых чисел бесконечное множество
элементов.
• Во множестве людей на Солнце нет элементов.

10.

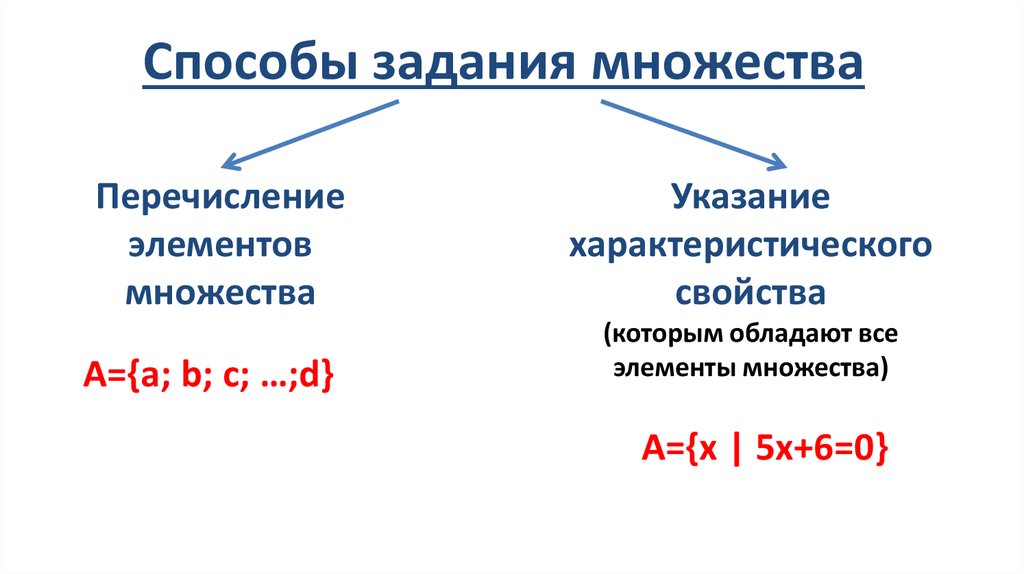
Способы задания множества
Перечисление
элементов
множества
А={a; b; c; …;d}
Указание
характеристического
свойства
(которым обладают все
элементы множества)
А={х | 5х+6=0}

11. Определение: Характеристическим свойством называется свойство, которым обладает каждый элемент, принадлежащий множеству, и не

обладает ни один объект,
не принадлежащий этому множеству.
Обозначение: Р(х) характеристическое свойство элементов
данного множества А, то есть
А х / Р( х ) « А множество всех х, таких что Р(х)».

12. Задайте перечислением элементов множество: 1) A = {x | x N, 2x – 1 = 0}; 2) B = {x | x Z, | x | < 3}; 3) C = {x | x N, x ≤ 15,

Задайте перечислением элементов
множество:
1) A = {x | x N, 2x – 1 = 0};
2) B = {x | x Z, | x | < 3};
3) C = {x | x N, x ≤ 15, x = 7k, k Z}.

13. Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В.