Решение тригонометрических уравнений и неравенств

1. Решение тригонометрических уравнений и неравенств

2. 1. Имеет ли смысл выражение:

a2
а) arcsin 2
;
a 1
да
да
a 1
б) arccos
;
2
a
2
нет
в) arcsin ( 2 -1)2;
a2 1
г) arctg
.
a2
, при а≠0

3. 2. Решить уравнения:

а) sin x = - 1;
х
2
2 ,
1
б) cos х = ;
2
х
в) sin х = 0;
х ,
г) tg x = 1;
х
4
3
2 ,
,

4. 3. Решить неравенства:

1
а) cos t < ;
2
решение
б) sin t > - 1,3;
решение
в) cos t ≥ 0;
решение
г) tg t ≤ 1;
решение

5. 3. Решить неравенства:

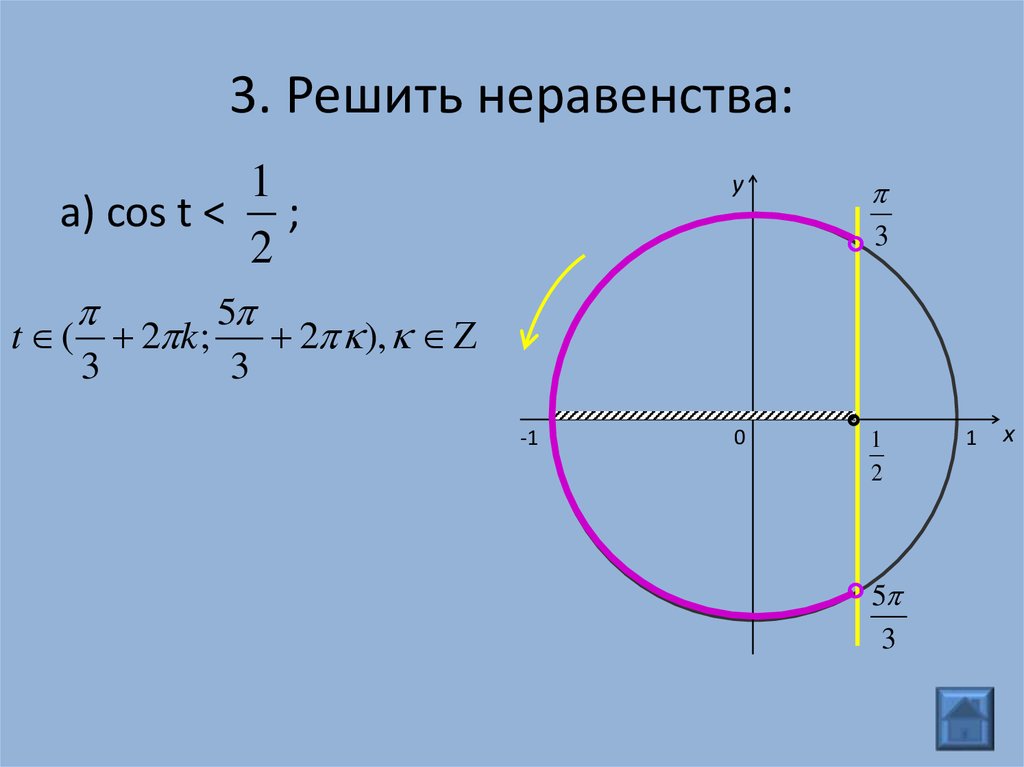
1
а) cos t < ;
2
y
3
0
1
2
5
t ( 2 k ;
2 ),
3
3
-1
5
3
1
x

6. 3. Решить неравенства:

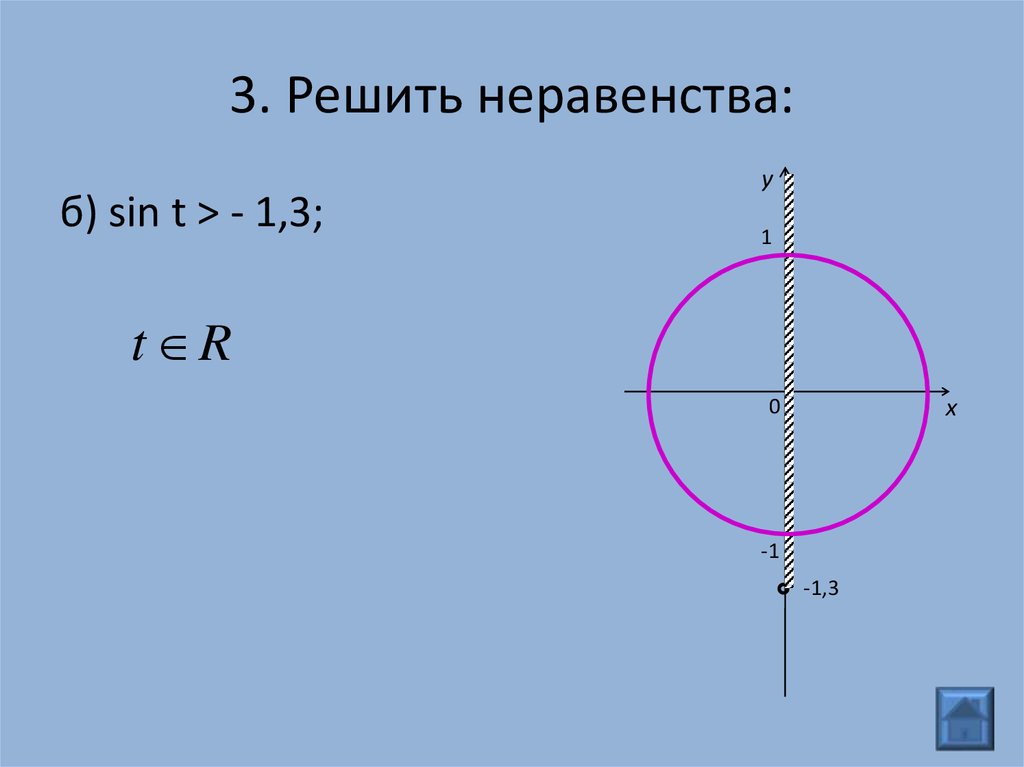
б) sin t > - 1,3;
y
1
t R
0
x
-1
-1,3

7. 3. Решить неравенства:

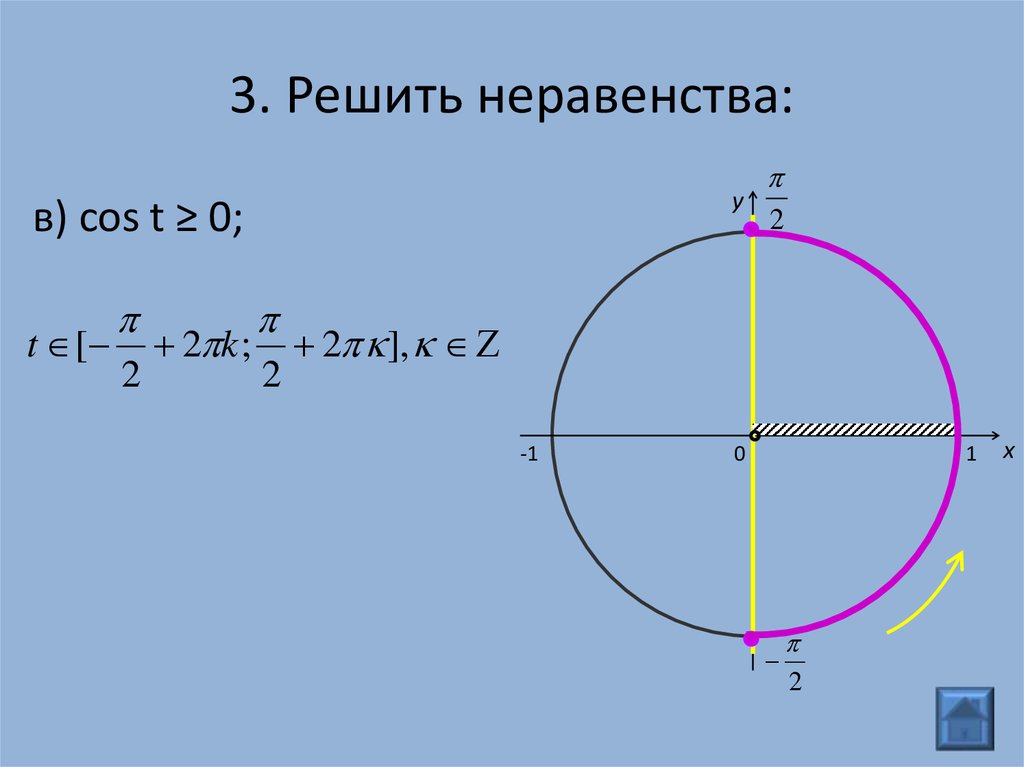
y
в) cos t ≥ 0;
t [
2
2 k ;
2
2
2 ],
-1
0
1
2
x

8. 3. Решить неравенства:

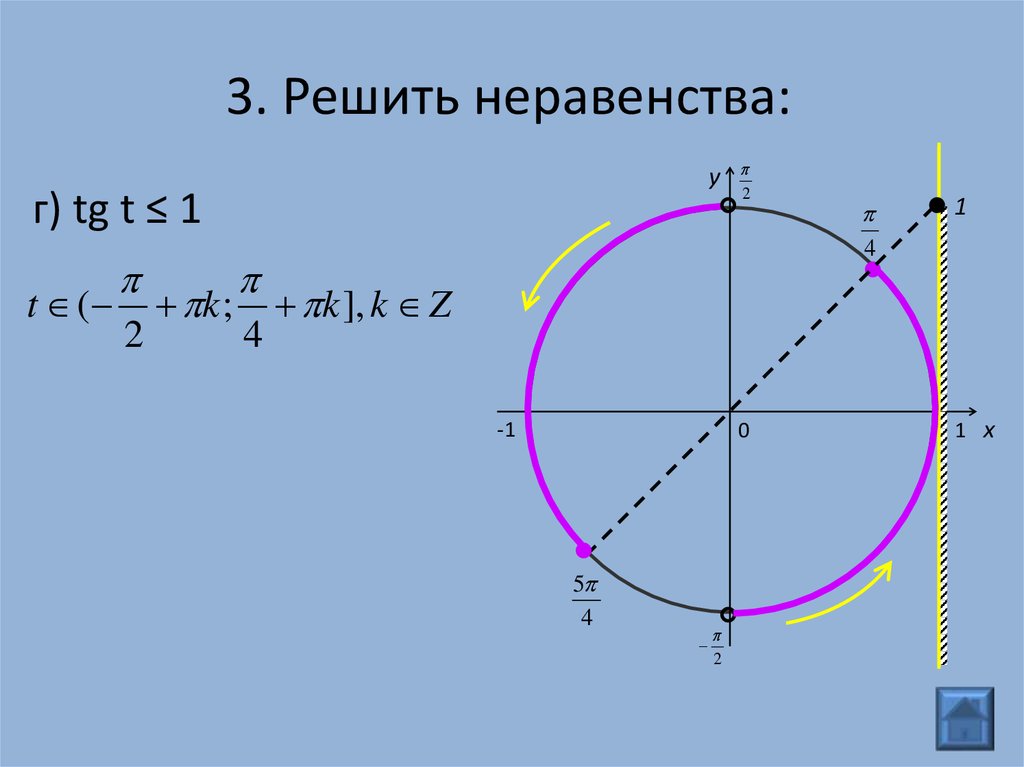
y
г) tg t ≤ 1
t (
2
k ;
4
2
4
1
k ], k Z
-1
0
5
4
2
1 x

9. 1. Назовите основные методы решения тригонометрических уравнений

• Введение новой переменной.
• Разложение на множители.
• Деление обеих частей уравнения на
cos(mx) для однородных уравнений
первой степени.
• Деление обеих частей уравнения на
cos2(mx) для однородных уравнений
второй степени.

10. №2. Решите уравнение

а) sin2x + 4cos x = 2,75;
решение
б) tg x + 3ctg x = 4;
решение
в) 2 sin х · cos х - cos2x = 0;
решение
г) 5 sin2x + sin х · cos х – 2 cos2x = 2.
решение

11.

а) sin2x + 4cos x = 2,75;
1 – cos2x + 4cos x = 2,75;
Пусть cos x = t, │t│≤ 1, тогда
t2 – 4t + 1,75 = 0;
D = 16 - 4·1,75 = 16 – 7 = 9;
( 4) 3
t
2
1
t 2 ,
t 3,5;
1
t
2
Вернёмся к исходной переменной:
1
cos x
2
x
3
2 k , k Z
Ответ : {
3
2 k / k Z }

12.

б) tg x + 3ctg x = 4;
3
tgx
4;
tgx
Пусть tg x = t, тогда
t2 – 4t + 3 = 0;
По свойству коэффициентов квадратного уравнения (a+b+c = 0):
t 1,
t 3;
Вернёмся к исходной переменной:
tgx 1,
tgx 3;
x 4 k , k Z ,
x arctg 3 n, n Z ;
Ответ : { k ,
4
arctg 3 n / k , n Z }

13.

в) 2 sin х · cos х - cos2x = 0;
cos х(2sinx – cosx) = 0;
cos x 0,
2 sin x cos x 0;
x 2 k , k Z ,
2tgx 1 0;
x 2 k , k Z ,
tgx 1 ;
2
/ : cos x 0
x 2 k , k Z ,
x arctg 1 n, n Z .
2
1
Ответ : { k , arctg n / k , n Z }
2
2

14.

г) 5 sin2x + sin х · cos х – 2 cos2x = 2;
5 sin2x + sin х · cos х – 2 cos2x = 2 cos2x + 2 sin2x;
3 sin2x + sin х · cos х – 4 cos2x = 0; / : cos 2 x 0
3tg2x + tg х – 4 = 0;
Пусть tg x = t, тогда
3t2 + t – 4 = 0;
По свойству коэффициентов
квадратного уравнения (a+b+c = 0):
t 1,
t 4 ;
3
Вернёмся к исходной переменной:
tgx 1,
tgx 4 ;
3
x 4 k , k Z ,
x arctg 4 n, n Z .
3
Ответ : { k ,
4
4
arctg n / k , n Z }
3

15. №3. Решите неравенство

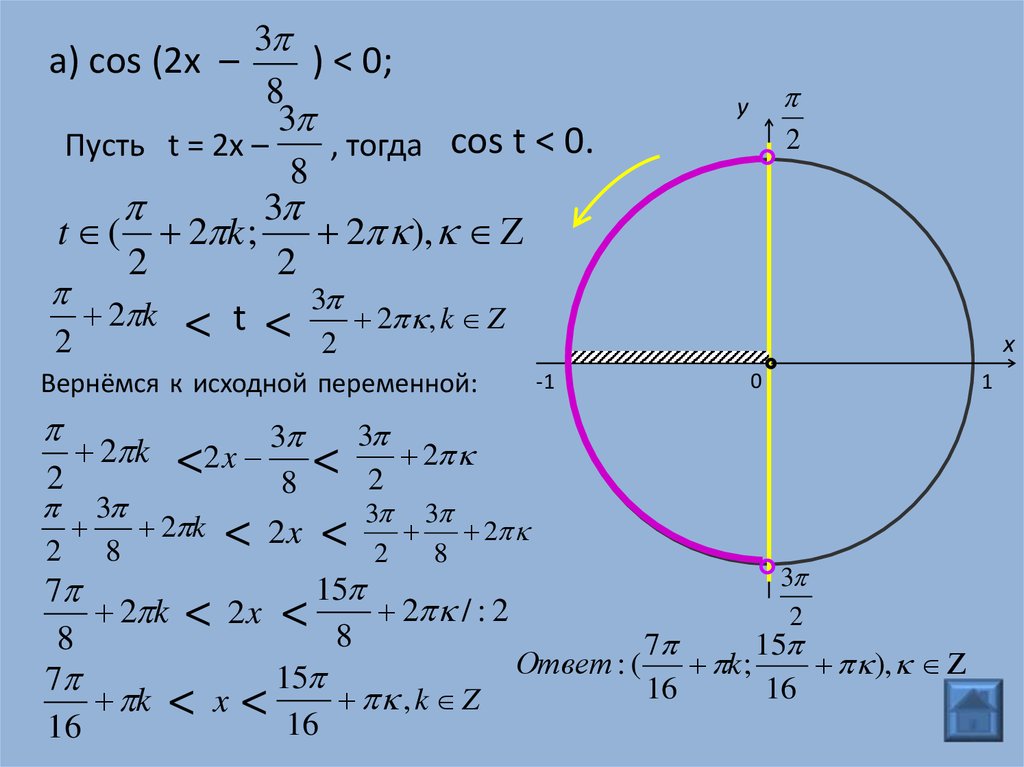
3
а) cos (2x ) < 0;
8
решение
1
б) sin x · cos3x + cos x ·sinx > ;
2
решение
в) sin x ≥ cos x;
решение
г) tg2 x ≤ 3.
решение

16.

3
а) cos (2x –
) < 0;
8
3
Пусть t = 2х –
, тогда cos t < 0.
8
3
t ( 2 k ;
2 ),
2
2
2 k < t < 3 2 , k Z
2
2
Вернёмся к исходной переменной:
3
<2 x 8
2
3
2 k < 2x
2
2
y
2 k
8
<
<
-1
x
0
3
2
2
3 3
2
2
8
3
15
7
2 / : 2
2 k < 2x <
2
8
8
7
15
Ответ : (
k ;
),
15
7
16
16
, k Z
k < x <
16
16
1

17.

1
б) sin x · cos3x + cos x ·sin3x > ;
2
1
sin(x + 3x) > ;
2
1
5
sin4x > ;
6
2
1
Пусть t = 4х, тогда sint > ;
2
5
t ( 2 k ;
2 ),
6
2 k
6
6
< t <
y
1
6
1
2
x
0
5
2 , k Z
6
Вернёмся к исходной переменной:
2 k
6
k
24 2
< 4x <
<x <
5
2 / : 4
6
5 k
24 2
-1
Ответ : (
24
k 5
;
2 24
k
2
),

18.

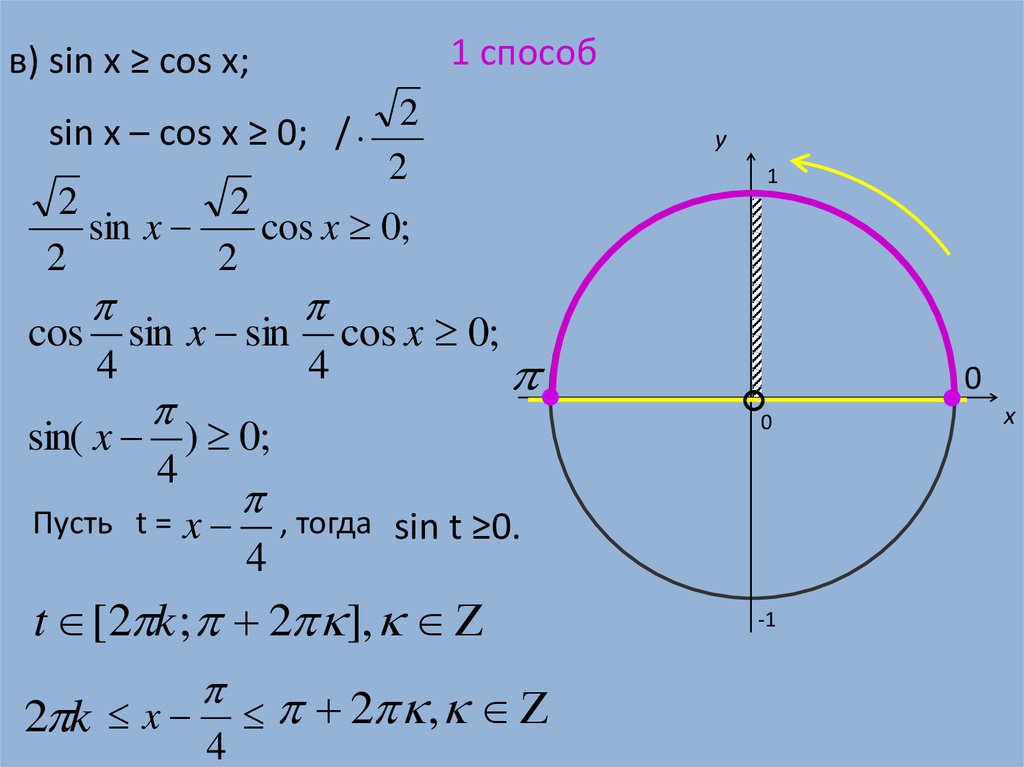
1 способ
в) sin x ≥ cos x;
sin x – cos x ≥ 0; /
2
2
y
1
2
2
sin x
cos x 0;
2
2
cos
4
sin x sin
4
cos x 0;
sin( x ) 0;
4
Пусть t = x , тогда sin t ≥0.
4
t [2 k ; 2 ],
2 k x
4
2 ,
0
0
-1
x

19.

2 k x
4
4
2
k
;
/
2 k x
4
4
2 k ;
5
2 k x
2 k ;
4
4
5
Ответ : [ 2 k ;
2 ],
4
4

20.

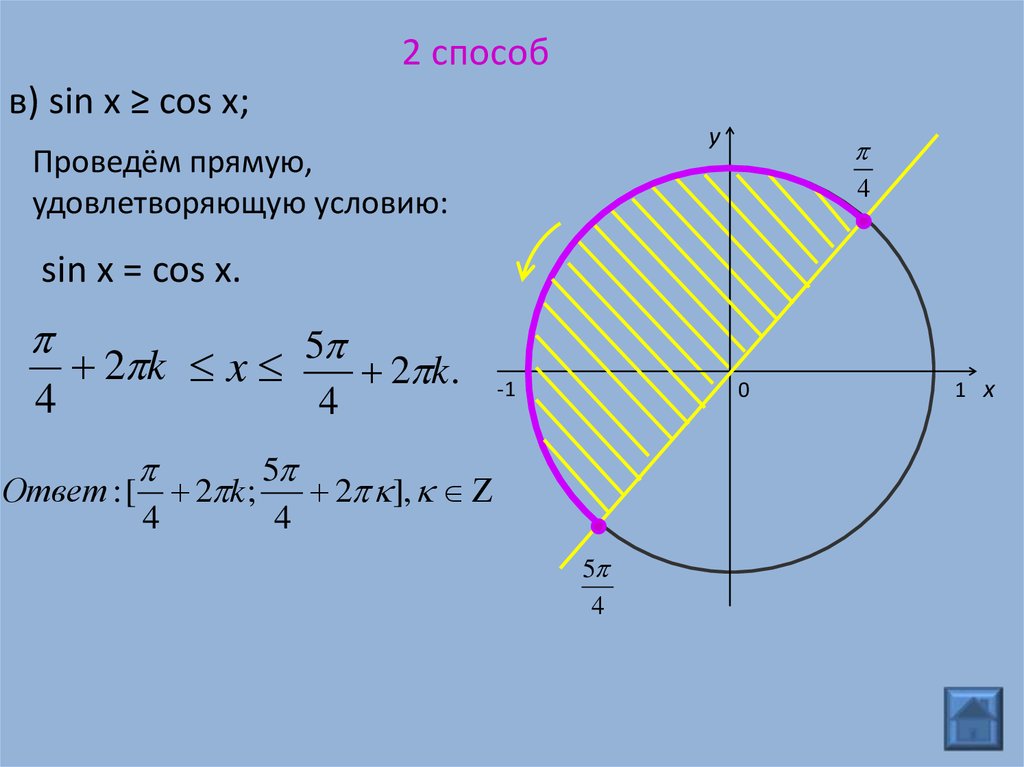
2 способ
в) sin x ≥ cos x;
y
Проведём прямую,
удовлетворяющую условию:
4
sin x = cos x.
5
2 k x
2 k .
4
4
-1
0
5
Ответ : [ 2 k ;
2 ],
4
4
5
4
1 x

21.

3
г) tg2 x ≤ 3;
2
3
tgx 3;
3
y
3 tgx 3;
x [
3
k ;
3
],
-1
Ответ : [
3
k ;
3
1 x
0
],
4
3
3
3