Похожие презентации:
Конус. Элементы конуса
1. Конус
Подготовила:учитель математики
МОУ сош №30 имени А.И.Колдунова
Кутоманова Е.М.
2010-2011 учебный год
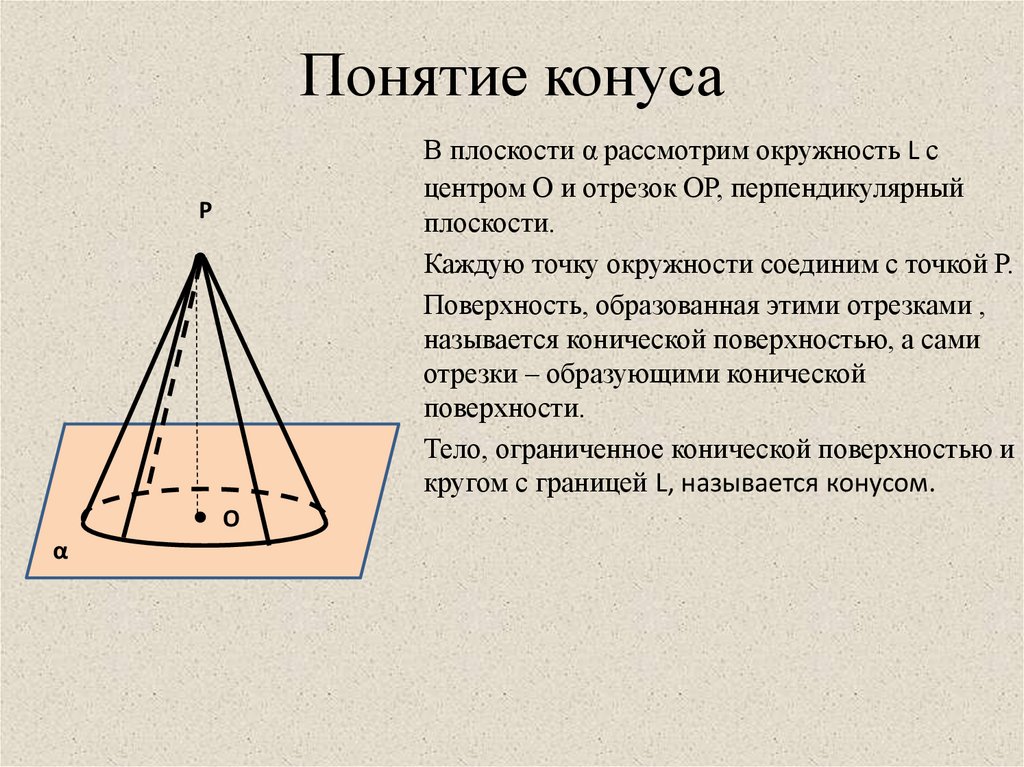
2. Понятие конуса
В плоскости α рассмотрим окружность L сцентром О и отрезок ОР, перпендикулярный
плоскости.
Каждую точку окружности соединим с точкой Р.
Поверхность, образованная этими отрезками ,
называется конической поверхностью, а сами
отрезки – образующими конической
поверхности.
Тело, ограниченное конической поверхностью и
кругом с границей L, называется конусом.
Р
О
α
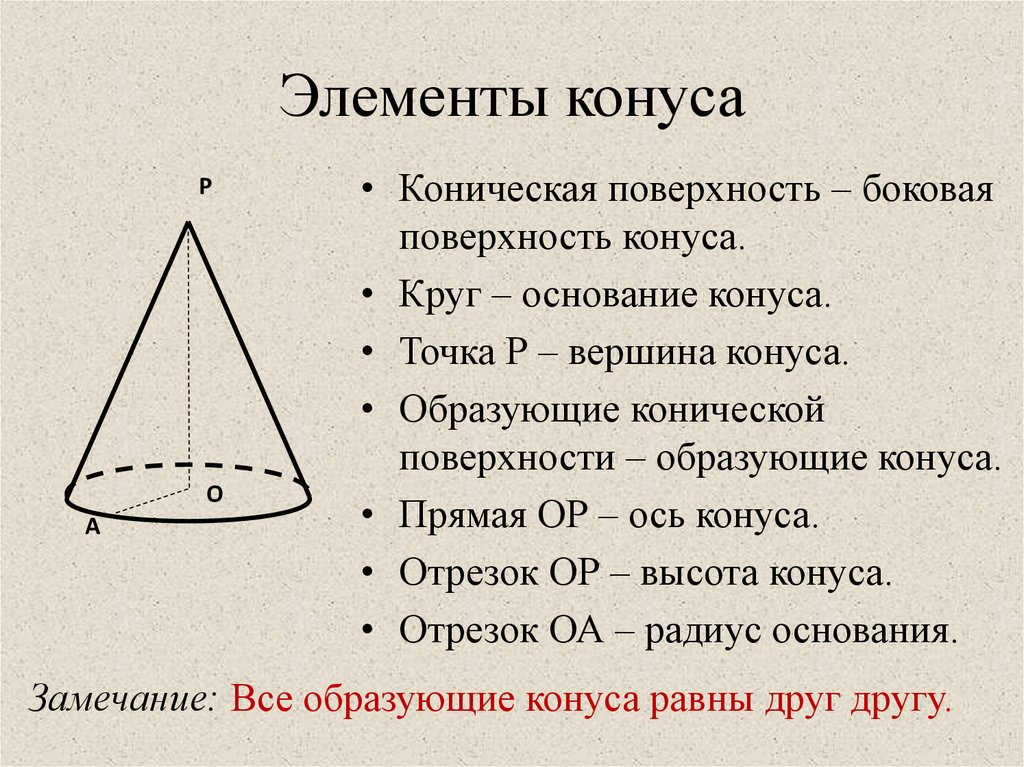
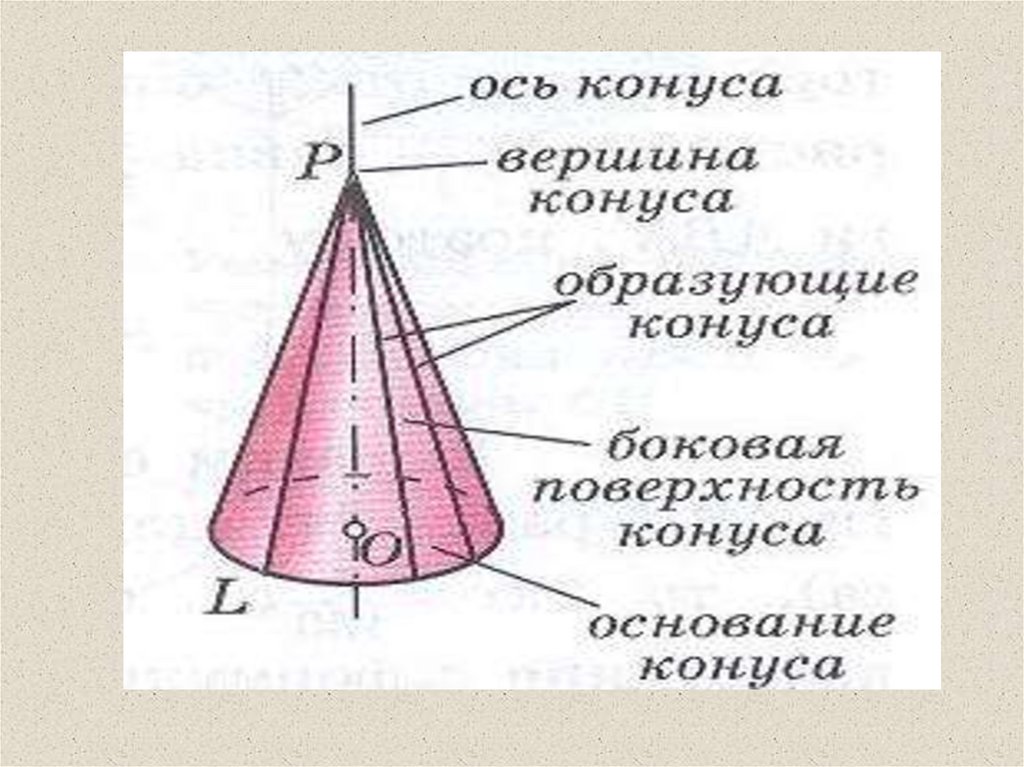
3. Элементы конуса
РО
А
• Коническая поверхность – боковая
поверхность конуса.
• Круг – основание конуса.
• Точка Р – вершина конуса.
• Образующие конической
поверхности – образующие конуса.
• Прямая ОР – ось конуса.
• Отрезок ОР – высота конуса.
• Отрезок ОА – радиус основания.
Замечание: Все образующие конуса равны друг другу.
4.
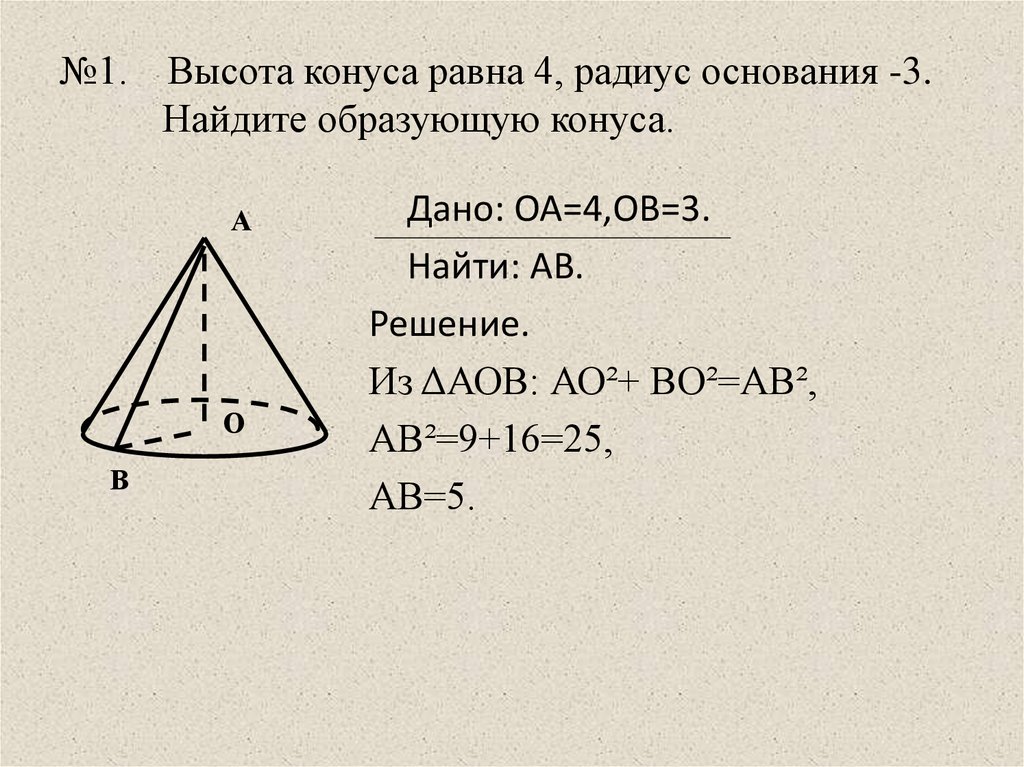
5. №1. Высота конуса равна 4, радиус основания -3. Найдите образующую конуса.
АО
В
Дано: ОА=4,ОВ=3.
Найти: АВ.
Решение.
Из ΔАОВ: АО²+ ВО²=АВ²,
АВ²=9+16=25,
АВ=5.
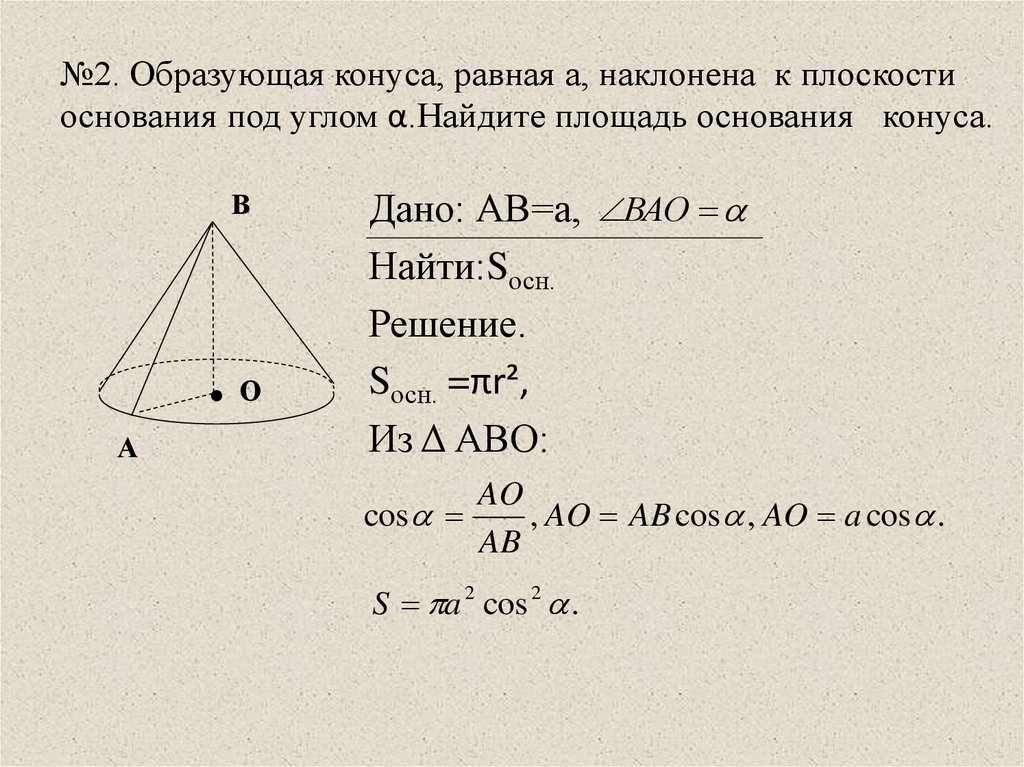
6. №2. Образующая конуса, равная а, наклонена к плоскости основания под углом α.Найдите площадь основания конуса.
ВО
А
Дано: АВ=а, ВАО
Найти:Sосн.
Решение.
Sосн. =πr²,
Из Δ АВО:
AO
cos
, AO AB cos , AO a cos .
AB
S a 2 cos 2 .
7. Конус – тело вращения…
АКонус можно получить путем
вращения прямоугольного
треугольника вокруг одного из
его катетов
С
8. Площадь боковой поверхности конуса
Площадь боковой поверхности конуса равнаплощади её развёртки – кругового сектора:
S
2
360
,
где - образующая конуса, α- градусная мера
дуги АВА´.
Длина дуги АВА´ равна длине окружности
основания конуса, т.е.
360r
2 360r
2 r
,
,S
r .
180
360
Sбок. = πrl
Площадь боковой поверхности конуса равна
произведению половины длины окружности
основания на образующую.
9. №3.Развёрткой боковой поверхности конуса является сектор с дугой α. Найдите α, если высота конуса равна 12, радиус основания 5.
Дано:h=12, r=5.
Найти:α.
360r
r 2 h 2 25 144 169 13,
360 5 1800
.
13
13
10.
Площадь полной поверхности конуса называетсясумма площадей боковой поверхности и основания.
Sпол. = πrl+ πr²= πr (r + l)
Sпол. = πr (r + l)
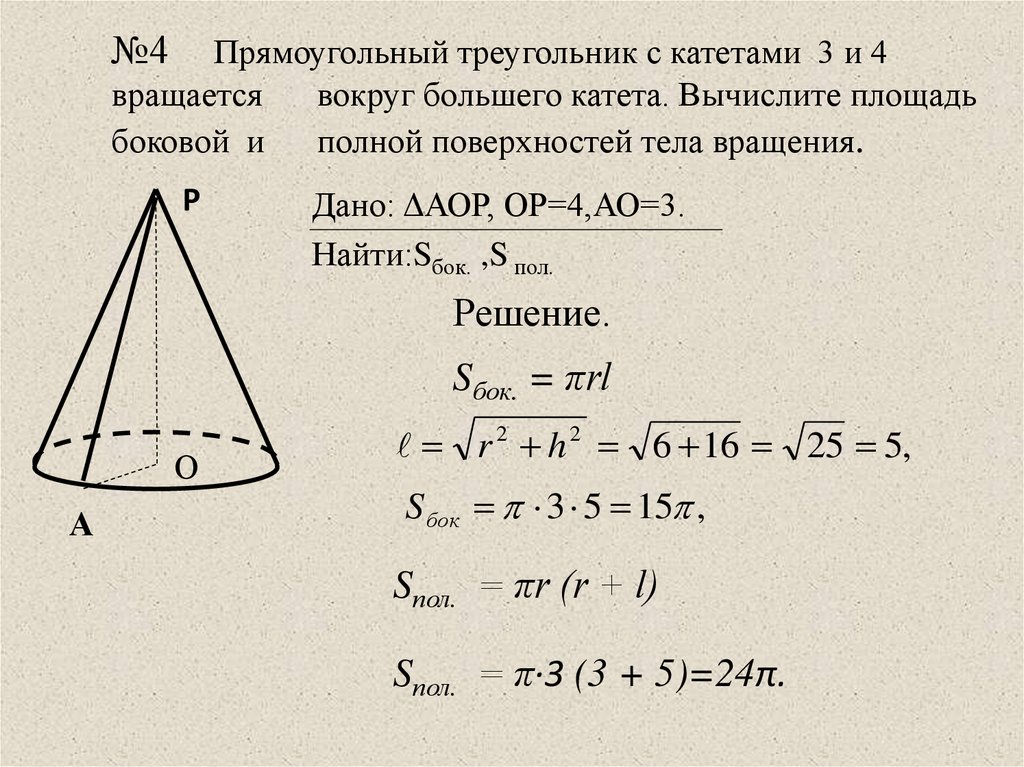
11. №4 Прямоугольный треугольник с катетами 3 и 4 вращается вокруг большего катета. Вычислите площадь боковой и полной поверхностей
тела вращения.Р
Дано: ΔАОР, ОР=4,АО=3.
Найти:Sбок. ,S пол.
Решение.
Sбок. = πrl
О
А
r 2 h 2 6 16 25 5,
S бок 3 5 15 ,
Sпол. = πr (r + l)
Sпол. = π·3 (3 + 5)=24π.
12. Сечение конуса различными плоскостями.
а)б)
в)
а) секущая плоскость проходит через ось конуса, осевое сечение
равнобедренный треугольник.
б) секущая плоскость проходит перпендикулярно к оси конуса, сечением
является круг.
в) сечение, пересекающее только одну часть кругового конуса и не
параллельное ни одной его образующей – эллипс.
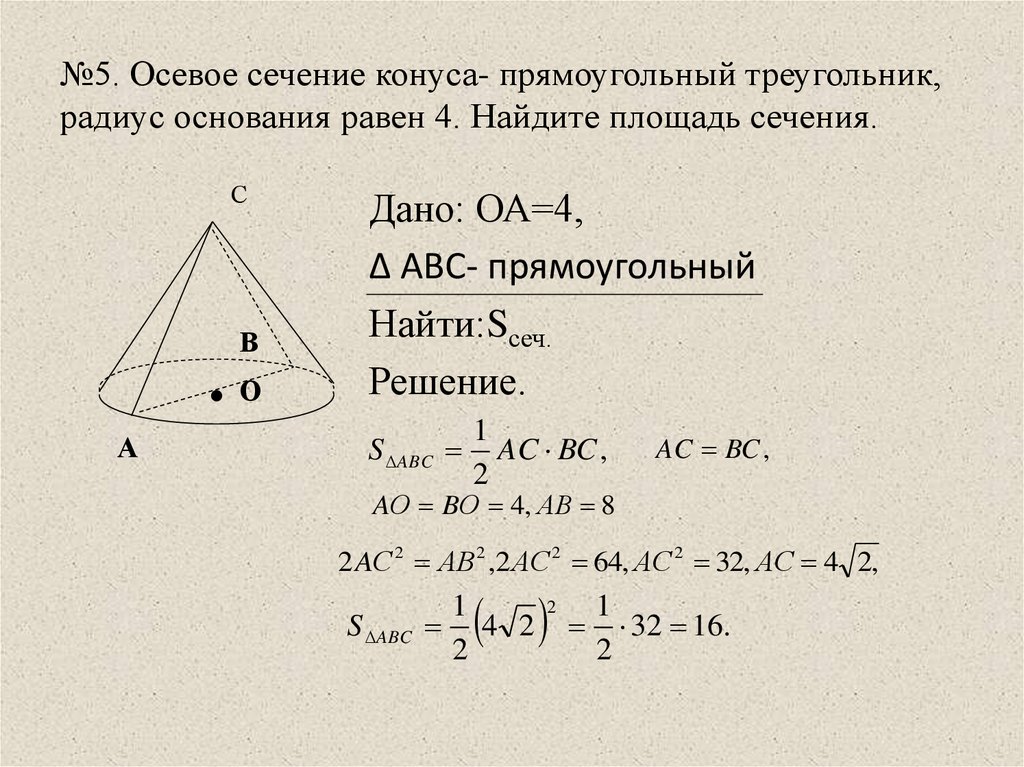
13. №5. Осевое сечение конуса- прямоугольный треугольник, радиус основания равен 4. Найдите площадь сечения.
СВ
О
А
Дано: ОА=4,
Δ АВС- прямоугольный
Найти:Sсеч.
Решение.
S ABC
1
AC BC ,
2
AC BC ,
AО BО 4, АВ 8
2 AС 2 АВ 2 ,2 АС 2 64, АС 2 32, АС 4 2,
S ABC
1
4 2
2
2
1
32 16.
2
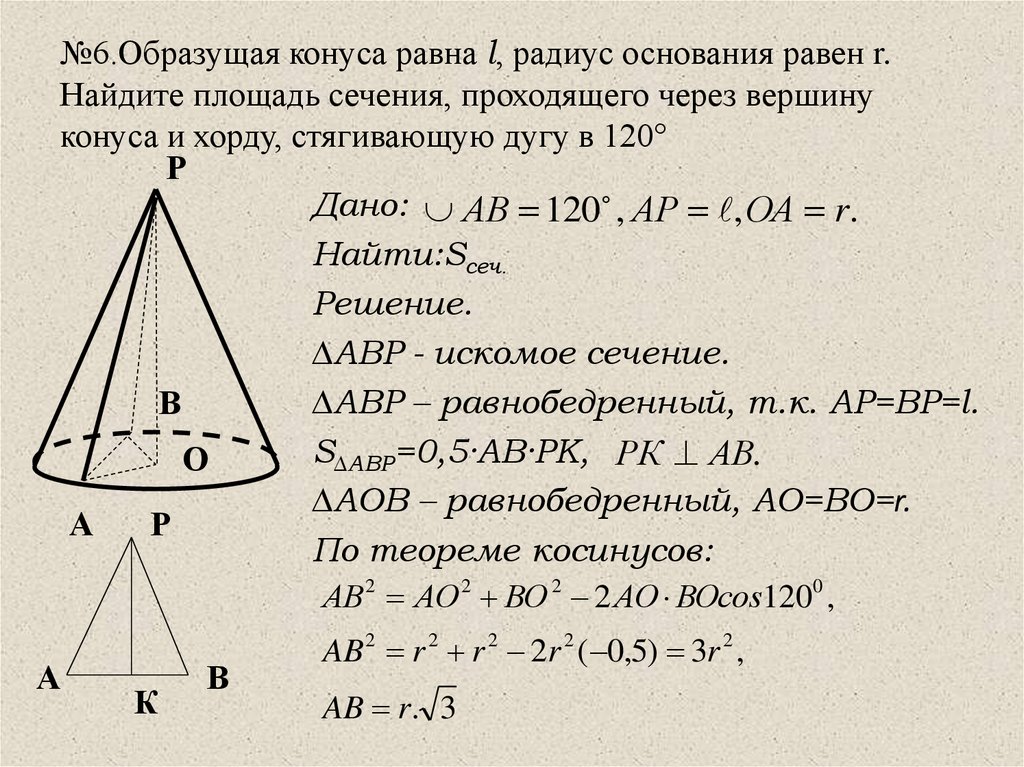
14. №6.Образущая конуса равна l, радиус основания равен r. Найдите площадь сечения, проходящего через вершину конуса и хорду,
стягивающую дугу в 120°Р
Дано: АВ 120 , АР , ОА r.
Найти:Sсеч.
Решение.
∆АВР - искомое сечение.
∆АВР – равнобедренный, т.к. АР=ВР=l.
В
S∆АВР=0,5·АВ·РК, РК АВ.
О
∆АОВ – равнобедренный, АО=ВО=r.
А
Р
По теореме косинусов:
АВ 2 АО 2 ВО 2 2 АО ВОсоs1200 ,
А
К
В
AB 2 r 2 r 2 2r 2 ( 0,5) 3r 2 ,
AB r. 3
15.
РАК
А
В
r 3
,
2
Из ∆АРК: РК²=АР²-АК²,
К
3r 2
РК
4
2
S сеч.
4 2 3r 2
4
4 2 3r 2
2
4 2 3r 2 r 12 2 9r 2
0,5 r 3
.
2
4
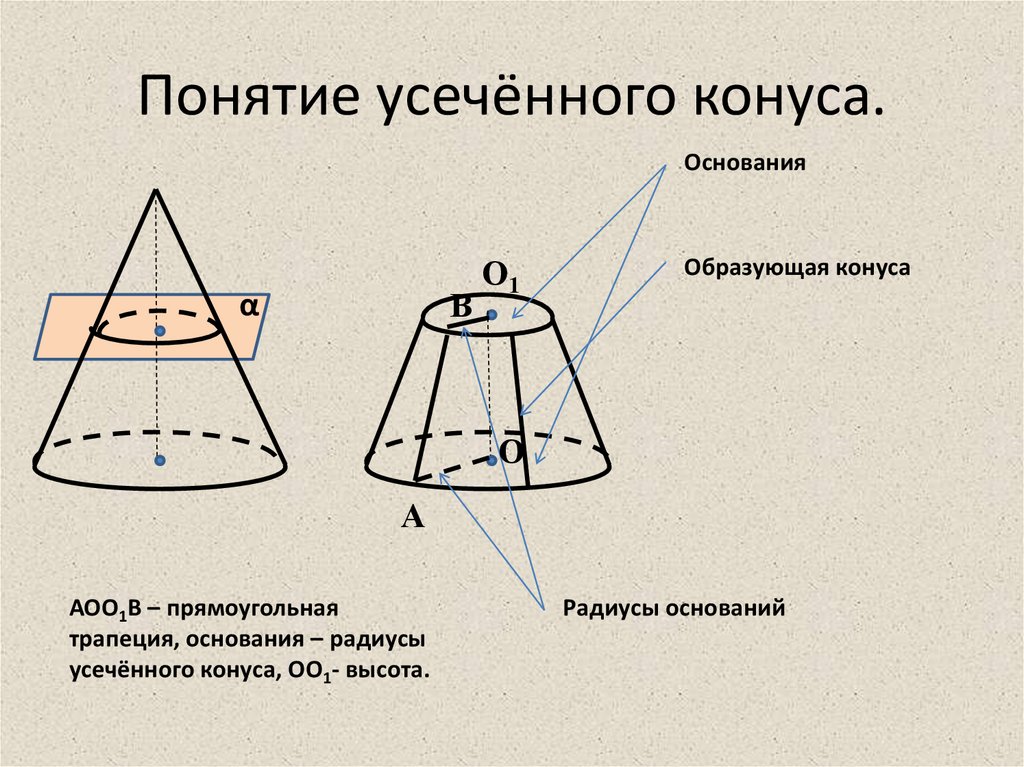
16. Понятие усечённого конуса.
ОснованияВ
α
О1
Образующая конуса
О
А
АОО1В – прямоугольная
трапеция, основания – радиусы
усечённого конуса, ОО1- высота.
Радиусы оснований
17.
Площадь боковой поверхностиусечённого конуса равна
произведению полусуммы длин
окружностей на образующую.
S бок. (r r1 )






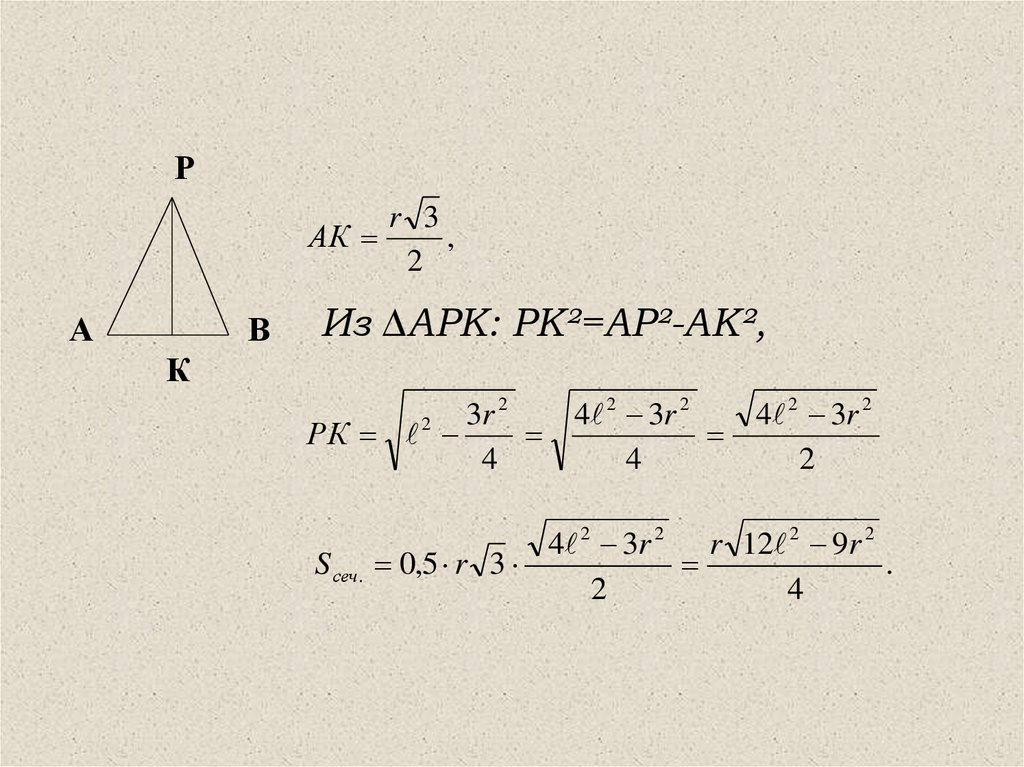

 Математика
Математика








