Похожие презентации:
Конус
1.
Ребята, здравствуйте!Прошу подготовиться к решению задач и
выполнить конспект в в тетради.
2. Повторите материал по теме: «Цилиндр. Площадь его поверхности». Ответьте на вопросы самопроверки.
3. Вопрос №1: Какая фигура является основанием цилиндра?
а) Овалб) Круг
в) Квадрат
4. Вопрос №2: Чему равна площадь основания цилиндра с радиусом 2см?
а) 4πб) 8π
в) 4
5. Вопрос №3: Как называется отрезок отмеченный красным цветом?
диагональ цилиндраб) апофема цилиндра
в)образующая
цилиндра
а)
6. Вопрос №4: По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRhб) 2πR(h+R)
2
в) πR h
7. Вопрос №5: По какой формуле можно вычислить полную поверхность цилиндра?
2а) πR h
б) 2πRh
в) 2πR(h+R)
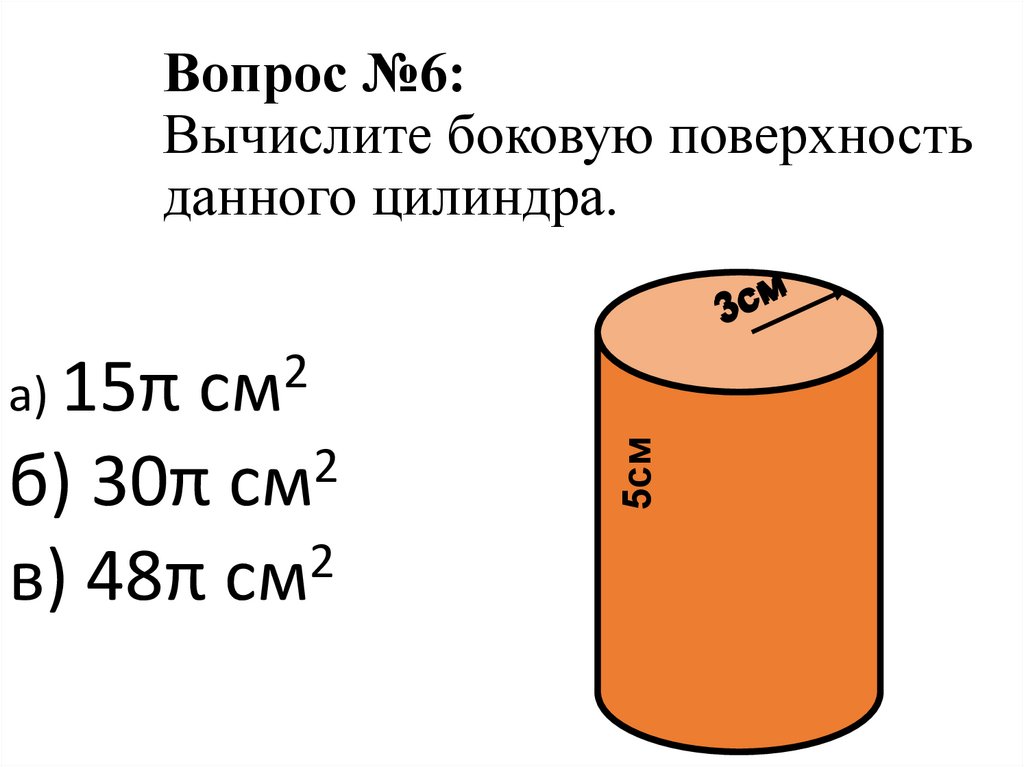
8. Вопрос №6: Вычислите боковую поверхность данного цилиндра.
2б) 30π см
2
в) 48π см
5см
2
а) 15π см
9. Вопрос №7: Вычислите полную поверхность данного цилиндра.
2б) 24π см
2
в) 16π см
6см
2
а) 32π см
10. Вопрос №8: Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей 3см?
2а) 6 см
2
б) 3 см
2
в) 6π см
11. Правильные ответы:
№вопроса
1
2
3
4
5
6
7
8
ответ
б
а
в
а
в
б
а
а
• На оценку «5»-8
правильных ответов.
• На оценку «4»- 6-7
правильных ответов.
• На оценку «3»- 5
правильных ответов.
• На оценку «2»- 4 и
менее правильных
ответов.
12. Тема
13.
Конус в переводе сгреческого «konos»
означает
«сосновая шишка».
14.
Определение:тело,
ограниченное
конической поверхностью и кругом с
границей L, называется конусом.
L
15.
Pвысота конуса (РО)
ось конуса
вершина конуса (Р)
боковая (коническая)
поверхность
образующие
r
B
основание конуса
радиус конуса (r)
16.
Конусообразные дома труллиОградительные
конусы
17. Палатка
18. Конус – тело вращения
Конус получаетсяпри вращении
прямоугольного
треугольника
вокруг катета
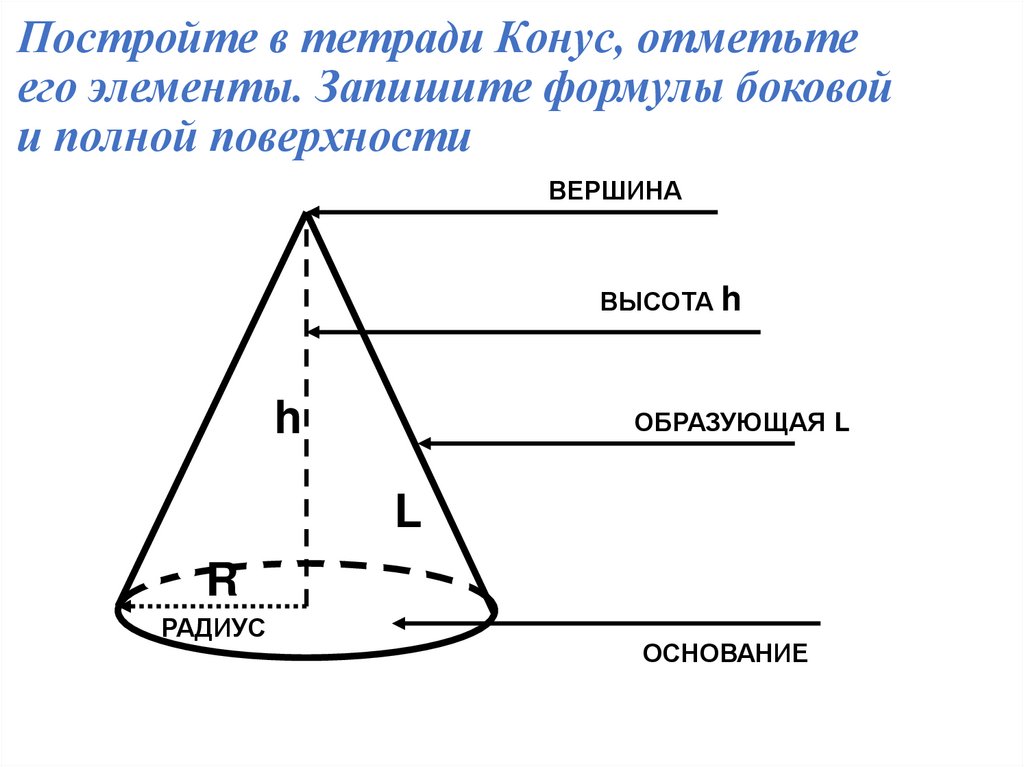
19. Постройте в тетради Конус, отметьте его элементы. Запишите формулы боковой и полной поверхности
ВЕРШИНАВЫСОТА h
h
ОБРАЗУЮЩАЯ L
L
R
РАДИУС
ОСНОВАНИЕ
20. Боковая поверхность конуса
• Если разрезать конус пообразующей, то получим
развертку конуса.
Sбок=πRL
C
L
A
B
21. Полная поверхность конуса
RSполн=Sбок+Sосн
Sбок=πRL
Sосн=πR2
Sполн=πRL+πR2
Sполн=πR(L+R)
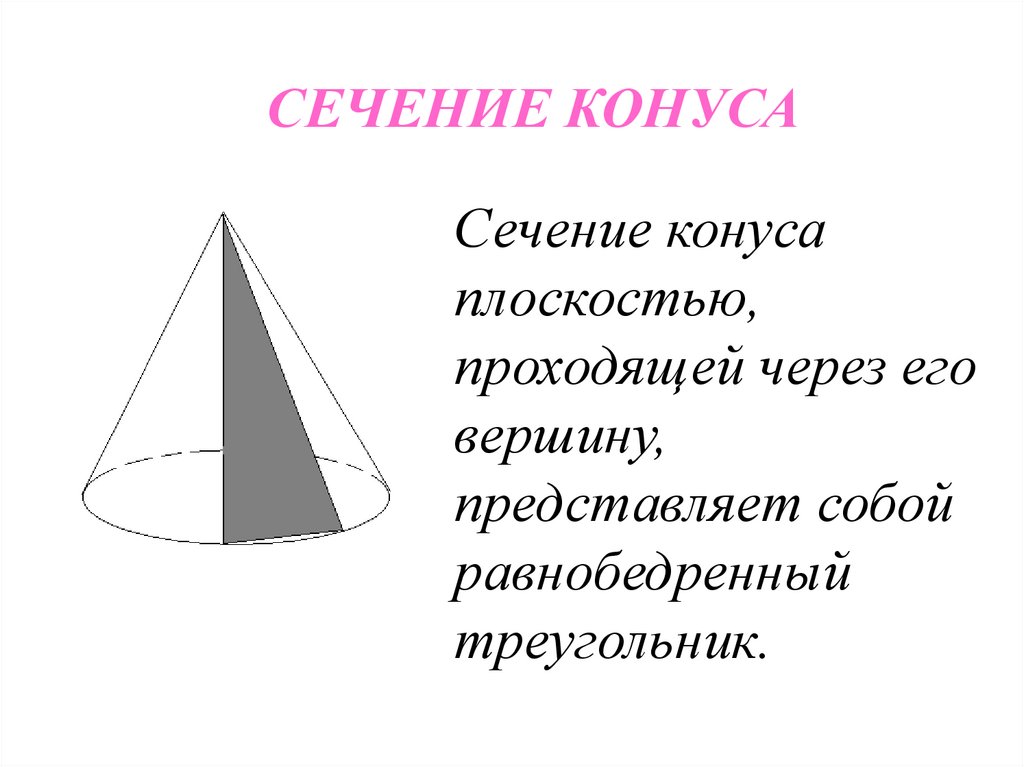
22.
СЕЧЕНИЕ КОНУСАСечение конуса
плоскостью,
проходящей через его
вершину,
представляет собой
равнобедренный
треугольник.
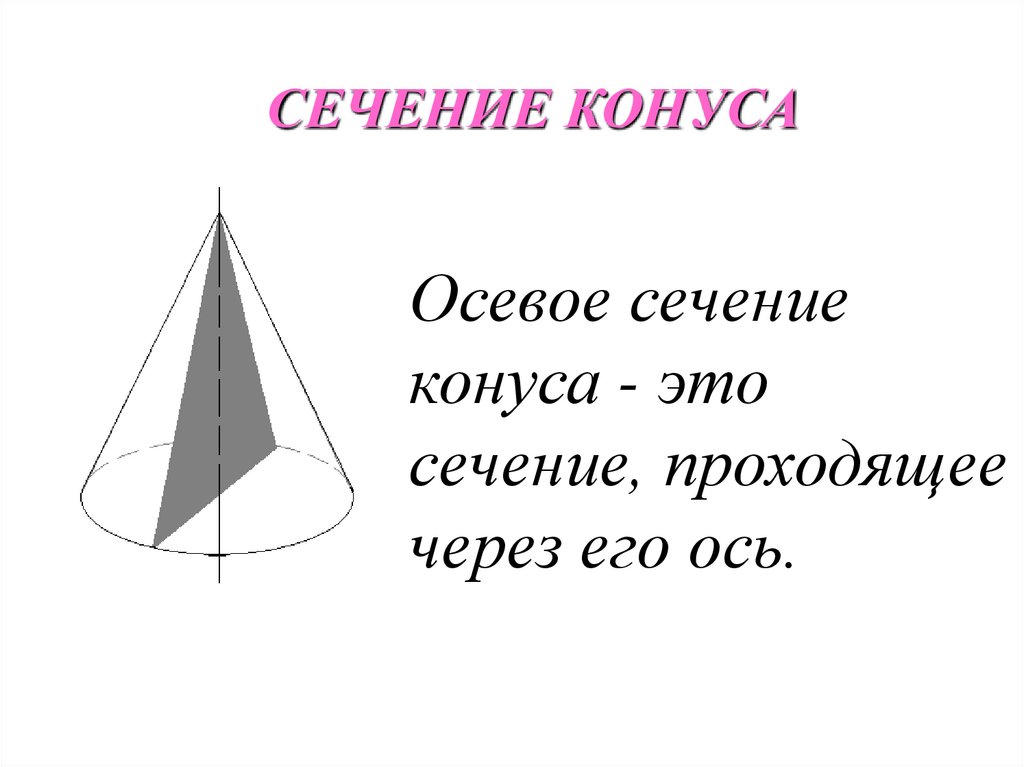
23.
СЕЧЕНИЕ КОНУСАОсевое сечение
конуса - это
сечение, проходящее
через его ось.
24.
СЕЧЕНИЕ КОНУСАСечение конуса
плоскостью,
параллельной его
основанию,
представляет собой
круг с центром на
оси конуса.
25. Домашнее задание
• Выполните опорный конспект в тетради• Ответьте на вопросы:
-Равны ли друг другу углы между
А) образующей конуса и плоскостью основания?
Б) образующей конуса и его осью?
- Что представляет собой сечение конуса плоскостью,
проходящей через вершину?
- Что представляет собой сечение конуса плоскостью,
перпендикулярно оси конуса?
- Чему равна площадь боковой и полной поверхности конуса?
- Где мы встречаемся с конусовидными поверхностями?





















 Математика
Математика








