Похожие презентации:
Сфера. Уравнение сферы
1.
1.2.
3.
Понятие сферы и её элементов
Уравнение сферы в заданной
системе координат
Решение задач по данной теме
2.
Политическая сфера – этосистема политических и
правовых отношений,
возникающих в обществе.
Социальная сфера - это система
социальных отношений, т.е.
отношений между группами
людей, занимающими различное
положение в социальной
структуре общества.
3.
Духовная сфера – этосистема отношений
между людьми,
отражающая духовнонравственную жизнь
общества,
представленную
такими подсистемами,
как культура, наука,
религия, мораль,
идеология, искусство.
4.
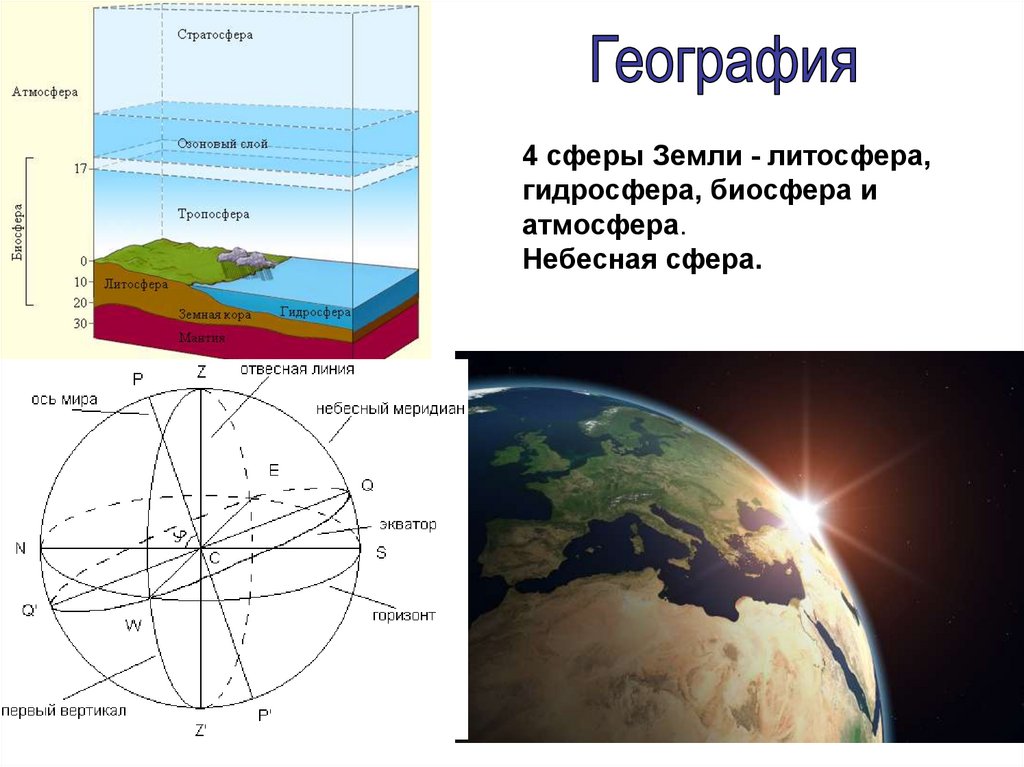
4 сферы Земли - литосфера,гидросфера, биосфера и
атмосфера.
Небесная сфера.
5.
6.
АС
О
Д
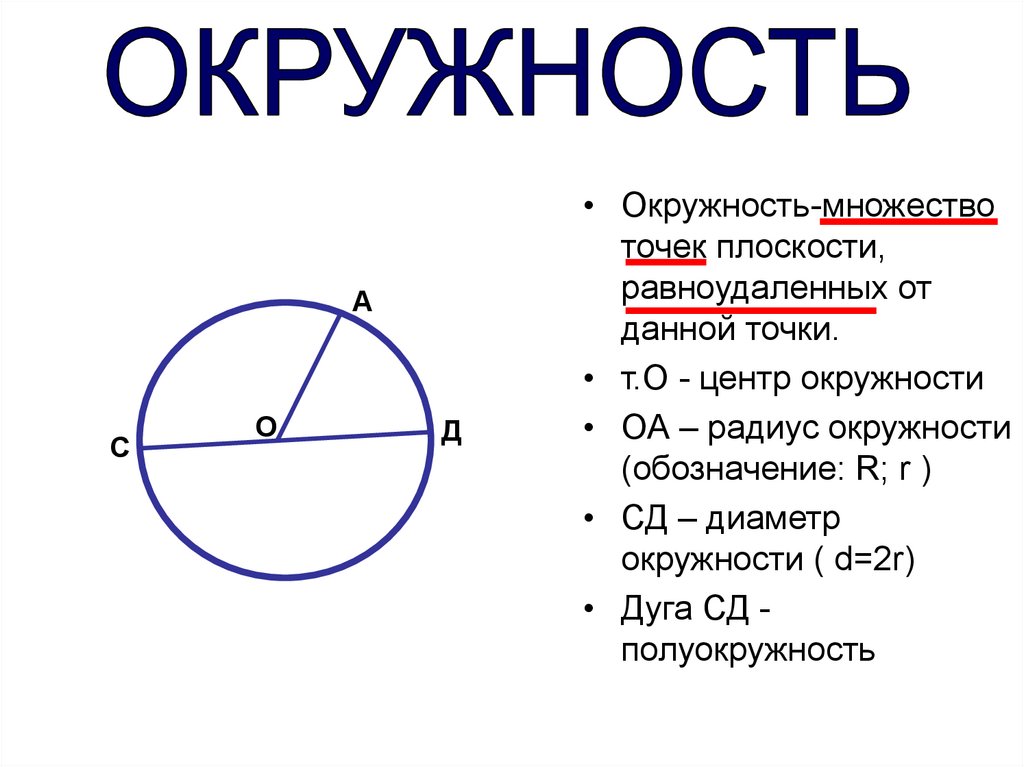
• Окружность-множество
точек плоскости,
равноудаленных от
данной точки.
• т.О - центр окружности
• ОА – радиус окружности
(обозначение: R; r )
• СД – диаметр
окружности ( d=2r)
• Дуга СД полуокружность
7.
8.
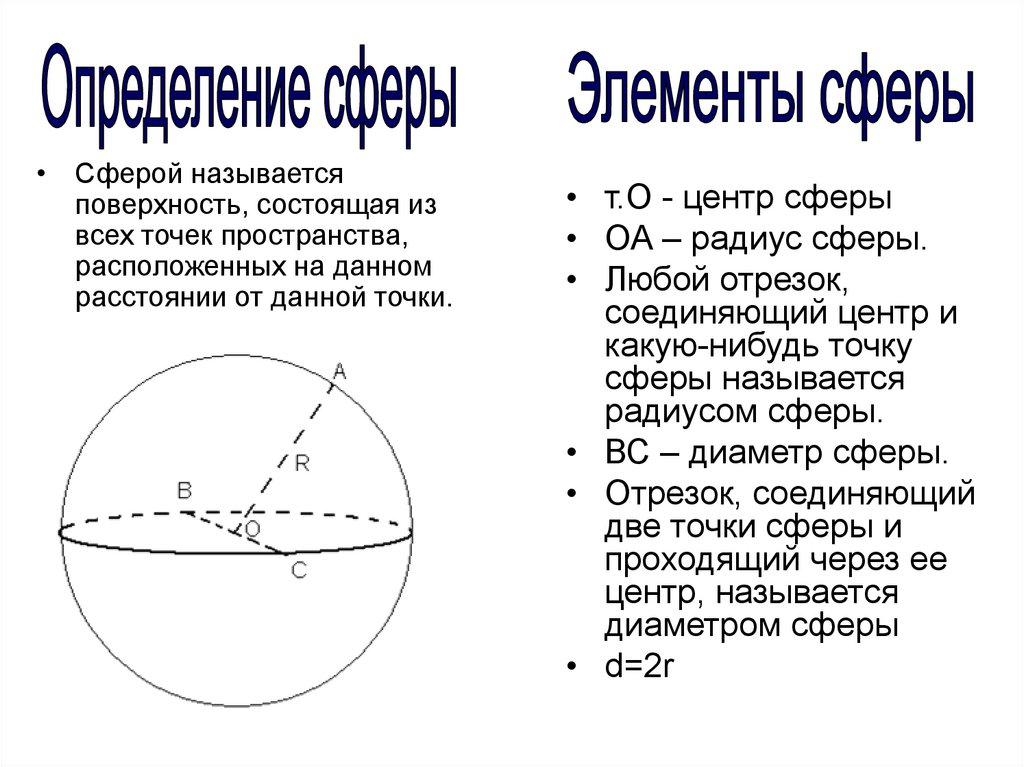
• Сферой называетсяповерхность, состоящая из
всех точек пространства,
расположенных на данном
расстоянии от данной точки.
• т.О - центр сферы
• ОА – радиус сферы.
• Любой отрезок,
соединяющий центр и
какую-нибудь точку
сферы называется
радиусом сферы.
• ВС – диаметр сферы.
• Отрезок, соединяющий
две точки сферы и
проходящий через ее
центр, называется
диаметром сферы
• d=2r
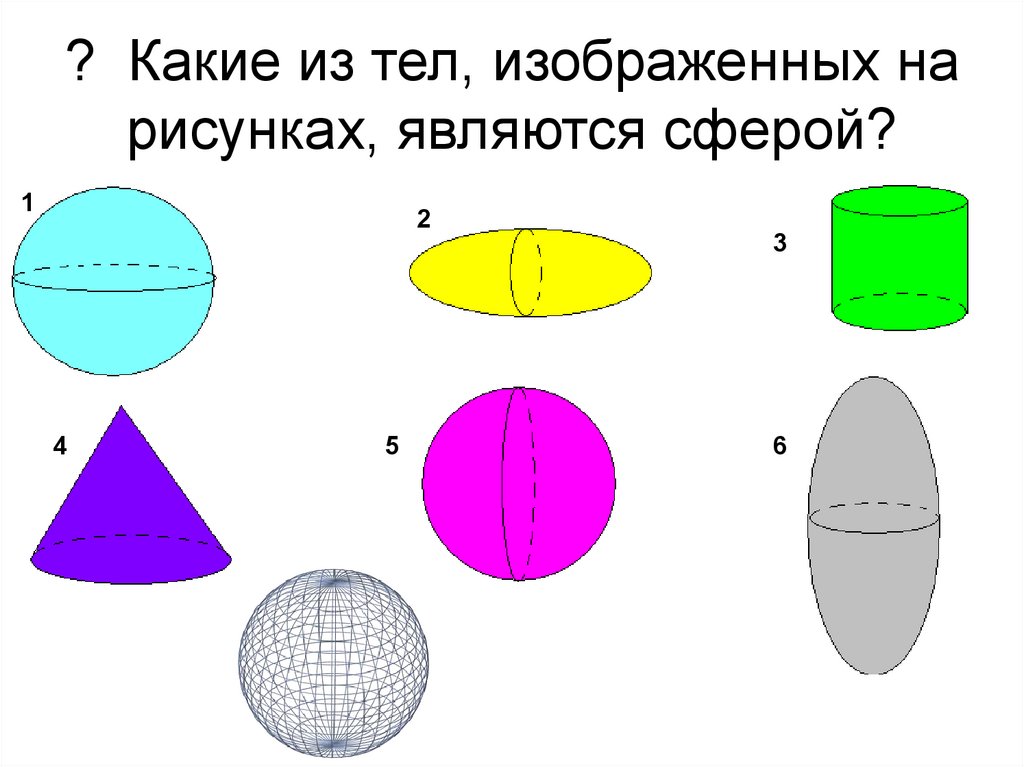
9. ? Какие из тел, изображенных на рисунках, являются сферой?
12
3
4
5
6
10.
11. №573(а)
• Точки А и В лежат на сфере с центромО, не принадлежащем АВ, а точка М
лежит на отрезке АВ. Докажите, что:
а) если М – середина отрезка АВ, то
ОМ ┴ АВ.
12. №574(а)
• Точка М – середина отрезка АВ, концыкоторого лежат на сфере радиуса R с
центром О. Найдите:
• а) ОМ, если R = 50 см, АВ = 40 см
13.
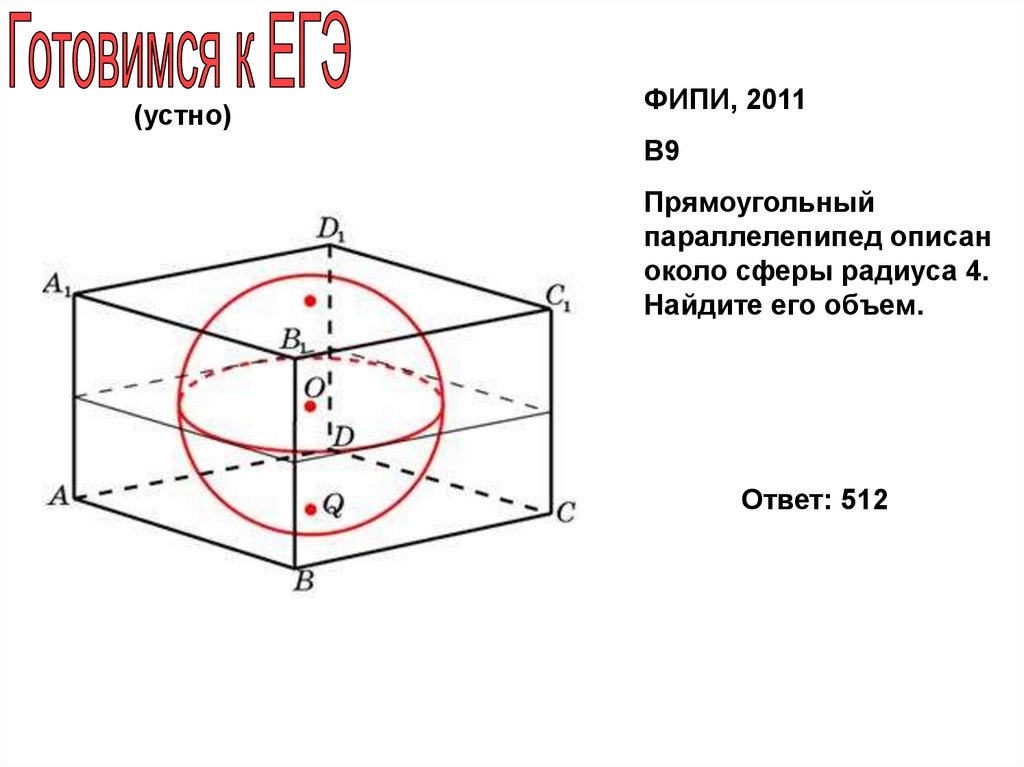
(устно)ФИПИ, 2011
В9
Прямоугольный
параллелепипед описан
около сферы радиуса 4.
Найдите его объем.
Ответ: 512
14.
zу
• М(х;у;z)
М(х;у)
у
L
х
Х
L
Сформулируйте
определение линии L на
плоскости
Сформулируйте
определение уравнения
поверхности в
пространстве
Уравнение с тремя переменными х,у,z
Уравнение с двумя переменными х и у
называется уравнением поверхности,
называется уравнением линии L, если
если этому уравнению удовлетворяют
этому уравнению удовлетворяют
координаты любой точки поверхности
координаты любой точки линии L и не
и не удовлетворяют координаты
удовлетворяют координаты никакой точки, никакой точки, не лежащей на этой
не лежащей на этой линии
поверхности
15.
уz
(х;у;z)
М(х;у)
С
х
х х0 у - у0
2
2
х - х 0 у - у0 r 2
d
2
у
2
х
2
2
2
d х х0 у - у 0 z z0
2
2
2
х - х 0 у - у0 z z0 r 2
16. Частные случаи
• 1.Уравнениеокружности с центром в
т.О(0;0) и радиусом r
х у r
2
2
2
• 1.Уравнение сферы с
центром в т.О(0;0;0) и
радиусом R
х у z R
2
2
2
2
17. Выбрать из предложенных уравнений – уравнение сферы:
1.
2.
3.
4.
5.
6.
7.
8.
( х 1) 2 ( у 2) 2 4
( х 1)2 ( у 5)2 ( z 3)2 22
2х 3у 6
( х 2)2 ( у 4)2 ( z 8) 2 9
2 х 2 5х 3 0
х 2 у 2 z 2 16
( х 2) 2 ( у 4) 2 ( z 7) 2 9
х2 4х у 2 z 2 0
1.Ур-е окружности
2.Ур-е сферы
3.Ур-е прямой
4.Ур-е сферы
5.Ур-е параболы
6.Ур-е сферы
7.Ур-е сферы
8. ?
18. В данных уравнениях определите координаты центра сферы и радиус
• 1.( х 2) ( у 4) z 7 9
• 2.
( х 6) ( у 0,5) z 5
• 3.
х у ( z 1) 6
• 4.
х у z 49
2
2
2
2
2
2
2
2
2
2
2
2
19.
Составьте уравнение сферы последующим данным центра и радиуса
сферы:
1.Дано: С(-2;8;1);
R=11
2.Дано: А(3;-2;0);
R=0,7
3.Дано: О(0;0;0);
R=1
Проверяем ответы:
х 2 у 8 z 1 121
2
2
2
х 3 у 2 z 0,49
2
2
х у z 1
2
2
2
2
20. Задача
• Определить принадлежит ли т.Асфере, заданной уравнением
( х 3) ( у 7) ( z 5) 30
2
2
2
если: а) т.А(5;-2;6)
б) т.А(-5;2;6)
5 3
2
Решение:
2 7 6 5 30
2
2
5 3 2 7 6 5
2
2
2
30
Равенство верное,
следовательно А(5;-2;6)
принадлежит сфере
Равенство неверное,
следовательно А(5;-2;6)
не принадлежит сфере
21. №577
Напишите уравнение сферы сцентром А, проходящей через
точку N, если А(-2;2;0); N(5;0;-1)
22. №579 (а ,г )
• Докажите, что каждое из следующихуравнений является уравнением сферы.
Найдите координаты центра и радиус этой
сферы:
2
2
2
• а) х 4 х у z 0
• г) х 2 х у 2 3 у z 2 2 z 2,5
23. Домашнее задание:
• 1. В тетради «Теория»:• а)Выучить определение сферы и её элементов;
уравнение сферы.
б)Изобразить шар, сформулировать определение шара
и его элементов. (Помощь в учебнике на стр.129 п.58)
• 2. Выполнить упражнения: № 573(б); № 576(в);
577(в)
• Дополнительно (по желанию): найти информацию о
теле вращения – тор.

















 Математика
Математика








