Похожие презентации:
Признаки параллельности прямых. Свойства параллельных прямых. Решение задач
1. «Геометрия – витамин для мозга».
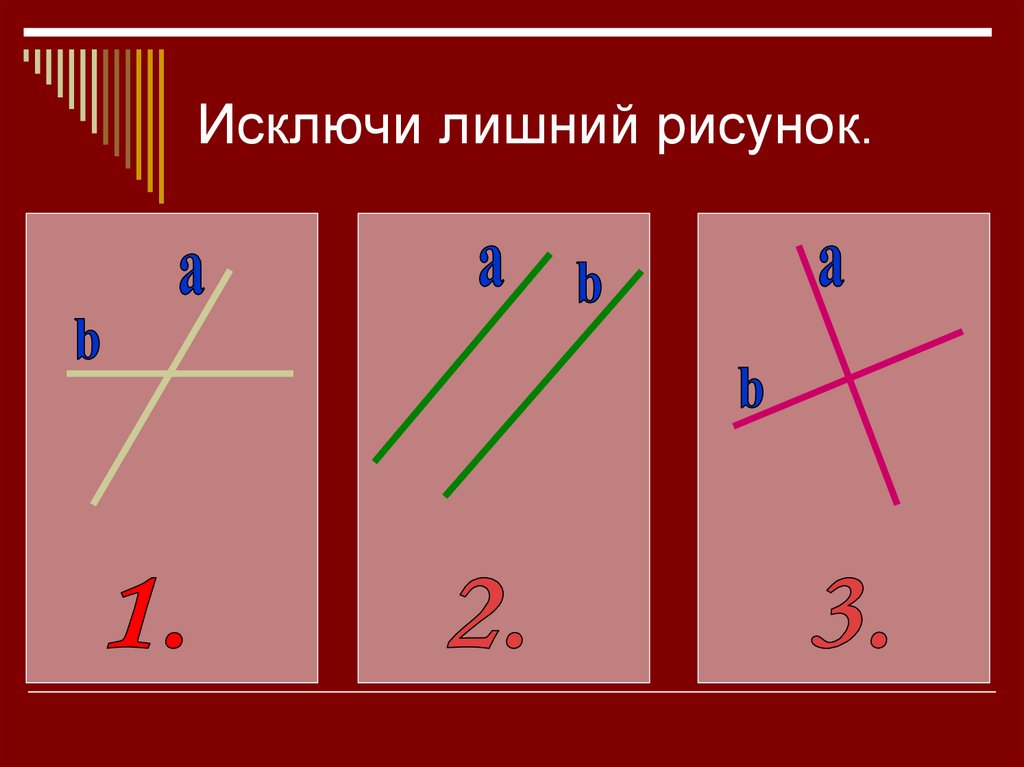
2. Исключи лишний рисунок.
3.
Являются ли параллельными красныегоризонтальные линии ?
4. Признаки параллельности прямых. Свойства параллельных прямых.
Тема урока:Признаки
параллельности
прямых.
Свойства
параллельных
прямых.
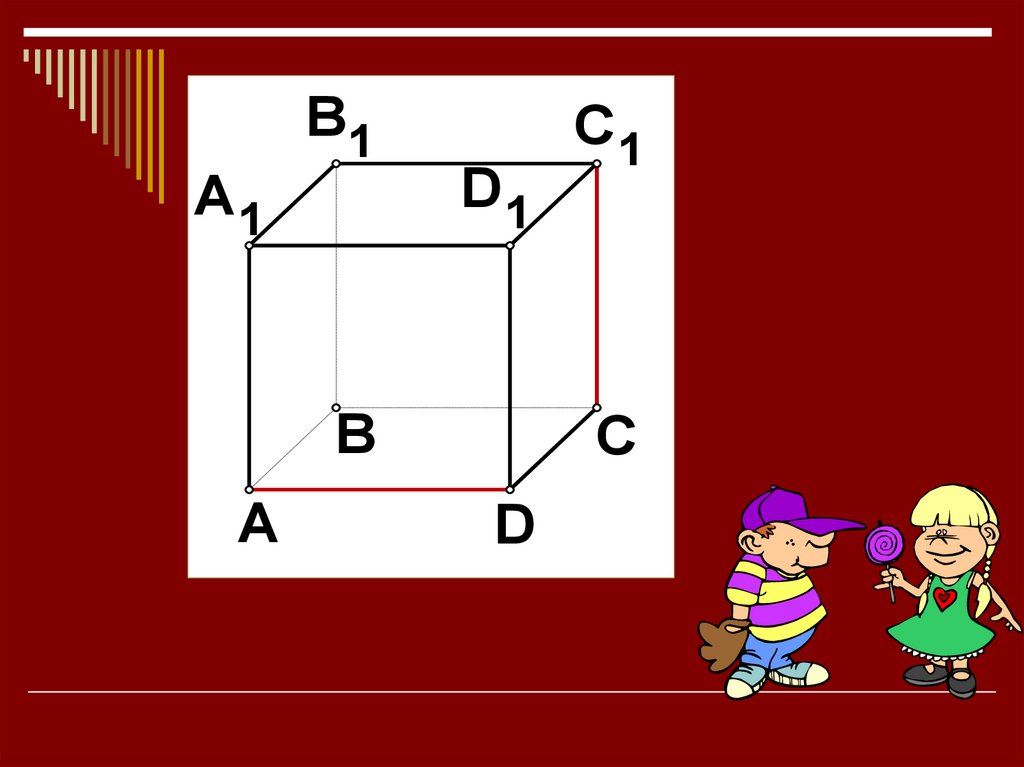
5.
A1B1
D1
B
A
C1
C
D
6. УСТАНОВИТЕ СООТВЕТСТВИЕ:
2и35и7
3и4
1и4
7и3
6и8
накрест лежащие
соответственные
односторонние
вертикальные
смежные
7и4
5и4
4и8
1и3
8и7
2и5
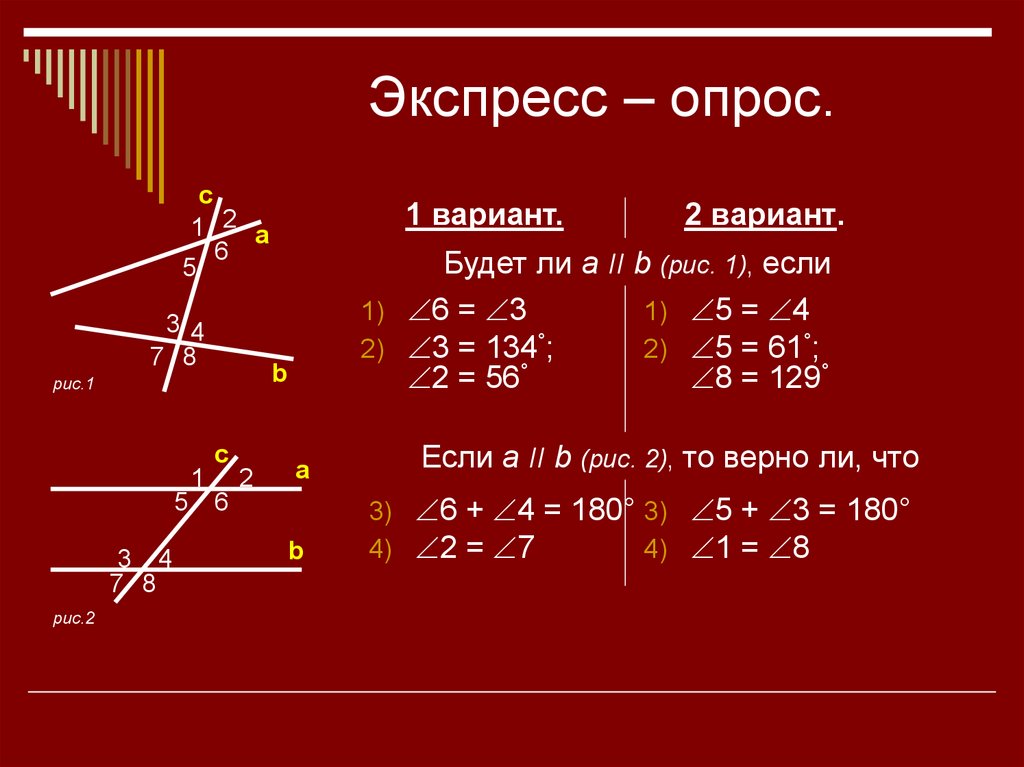
7. Экспресс – опрос.
c1 2 a
6
5
34
7 8
c
1
3 4
7 8
рис.2
2
2 вариант.
Будет ли a ׀׀b (рис. 1), если
1) 6 = 3
1) 5 = 4
2) 3 = 134°;
2) 5 = 61°;
2 = 56°
8 = 129°
b
рис.1
5
1 вариант.
a
6
b
Если a ׀׀b (рис. 2), то верно ли, что
3) 6 + 4 = 180° 3) 5 + 3 = 180°
4) 2 = 7
4) 1 = 8
8. Домашнее исследование.
Пируев ДмитрийСофонова Екатерина
Лаптев Борис
9. Решение задач по теме: «Признаки параллельности прямых. Свойства параллельных прямых.»
Подготовил: ученик 7б классаМОУ СОШ №10 г. Павлово
Пируев Дмитрий
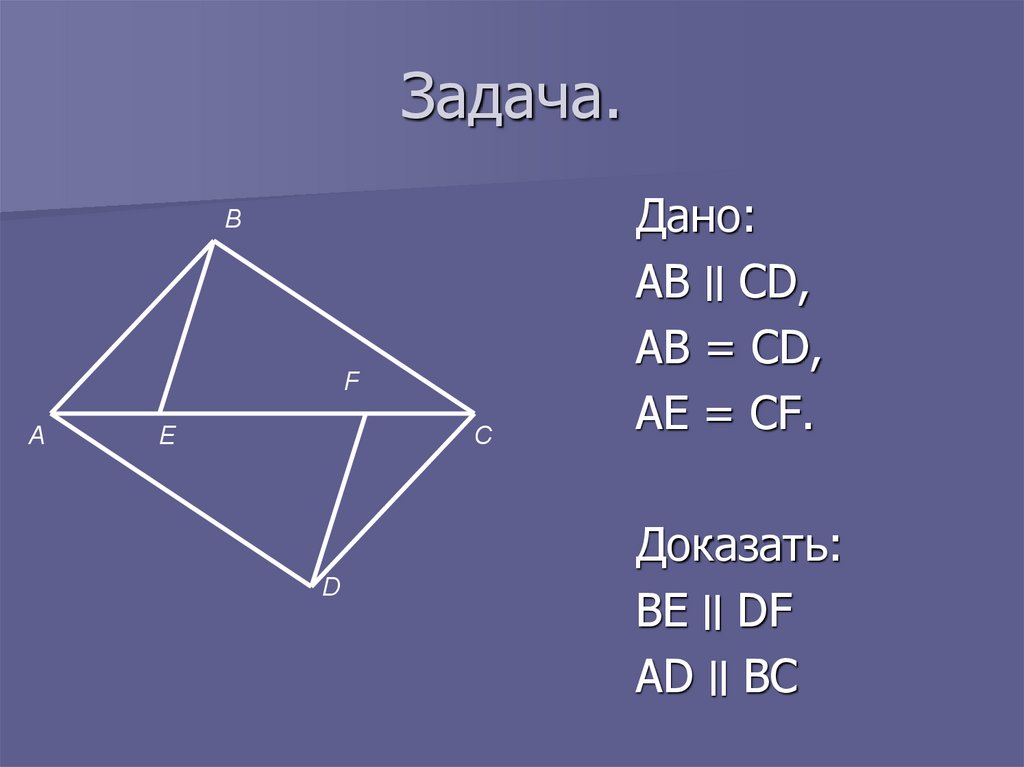
10. Задача.
ВF
А
Е
C
D
Дано:
АВ ׀׀CD,
AB = CD,
AE = CF.
Доказать:
BE ׀׀DF
AD ׀׀BC
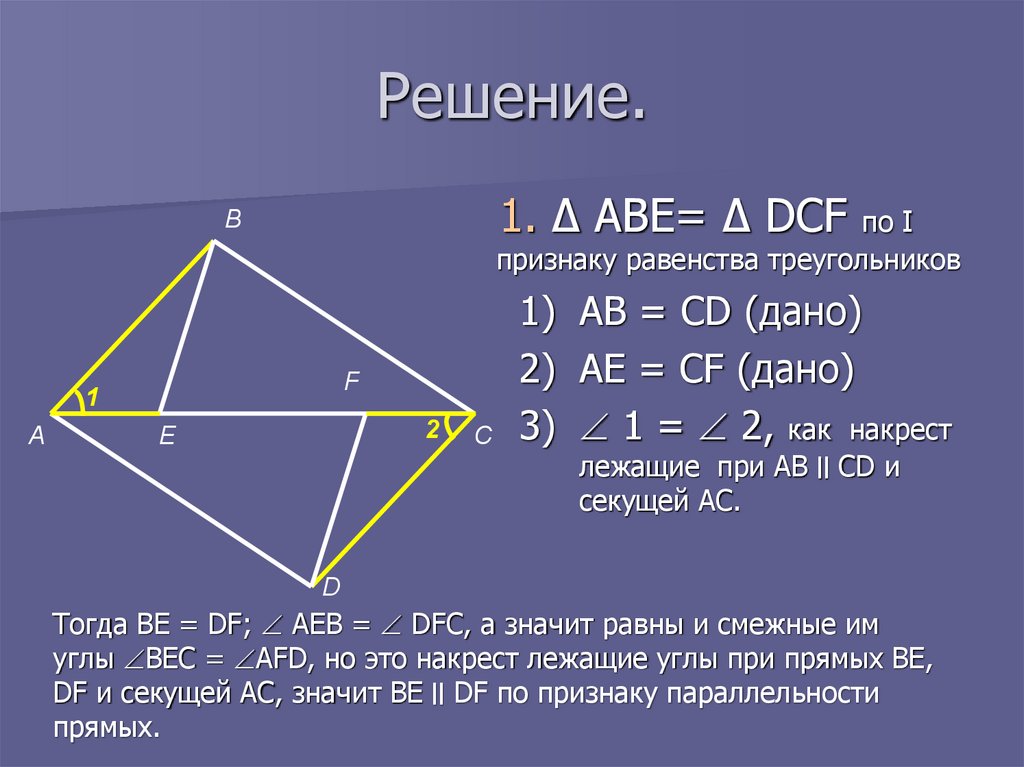
11. Решение.
1. Δ ABE= Δ DCFпо I
признаку равенства треугольников
В
F
1
А
2
Е
C
1) AB = CD (дано)
2) AE = CF (дано)
3) 1 = 2, как накрест
лежащие при AB ׀׀CD и
секущей AC.
D
Тогда BE = DF; AEB = DFC, а значит равны и смежные им
углы BEC = AFD, но это накрест лежащие углы при прямых ВЕ,
DF и секущей АС, значит ВЕ ׀׀DF по признаку параллельности
прямых.
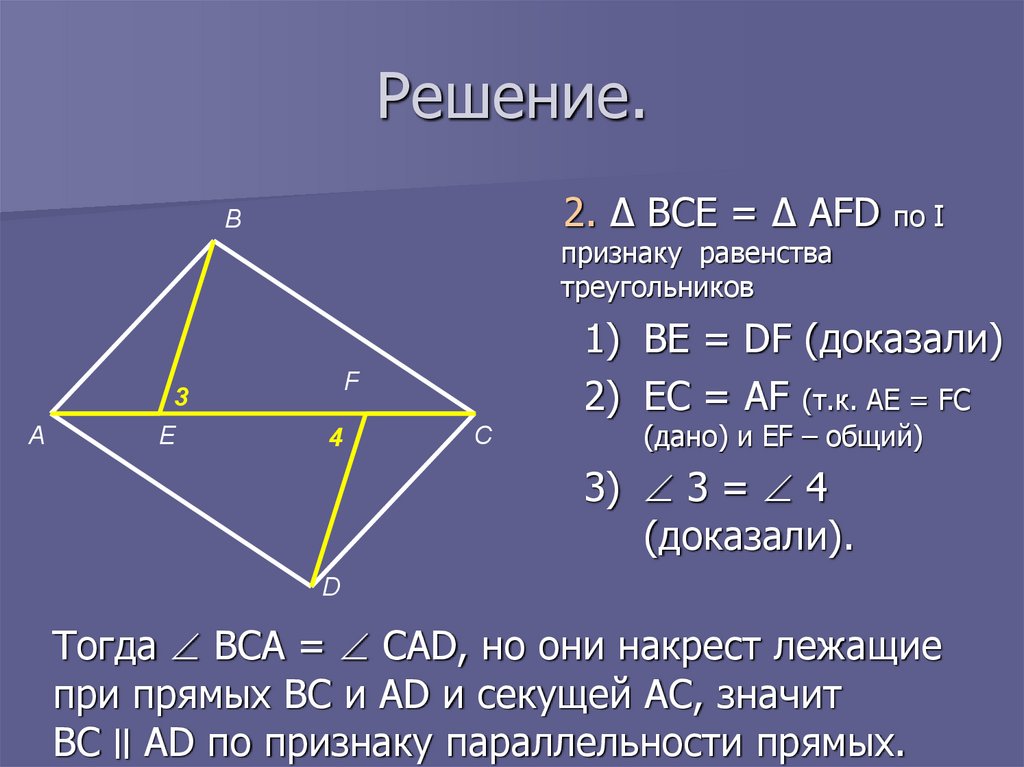
12. Решение.
2. Δ BCE = Δ AFDВ
по I
признаку равенства
треугольников
А
3
Е
1) BE = DF (доказали)
2) EC = AF (т.к. AE = FC
F
4
C
(дано) и ЕF – общий)
3) 3 = 4
(доказали).
D
Тогда BCA = CAD, но они накрест лежащие
при прямых BC и AD и секущей AC, значит
BC ׀׀AD по признаку параллельности прямых.
13. Групповая работа.
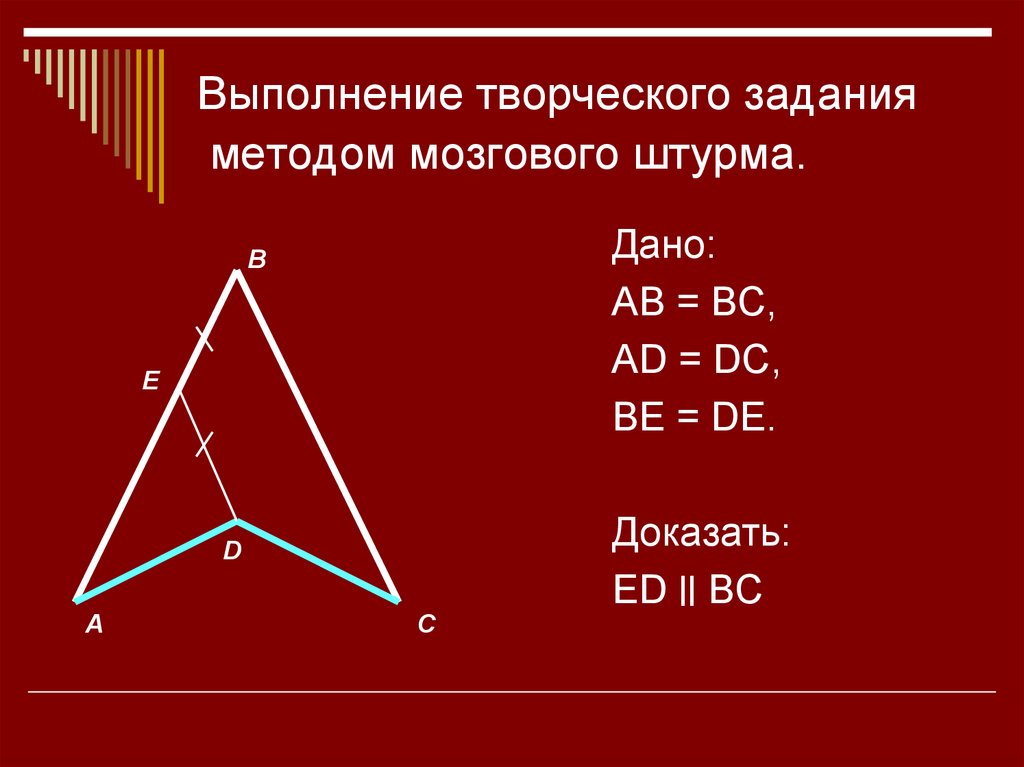
14. Выполнение творческого задания методом мозгового штурма.
Дано:AB = BC,
AD = DC,
BE = DE.
B
E
Доказать:
ED ׀׀BC
D
A
C







 Математика
Математика