Решение задач на применение признаков параллельности прямых

1. Решение задач на применение признаков параллельности прямых

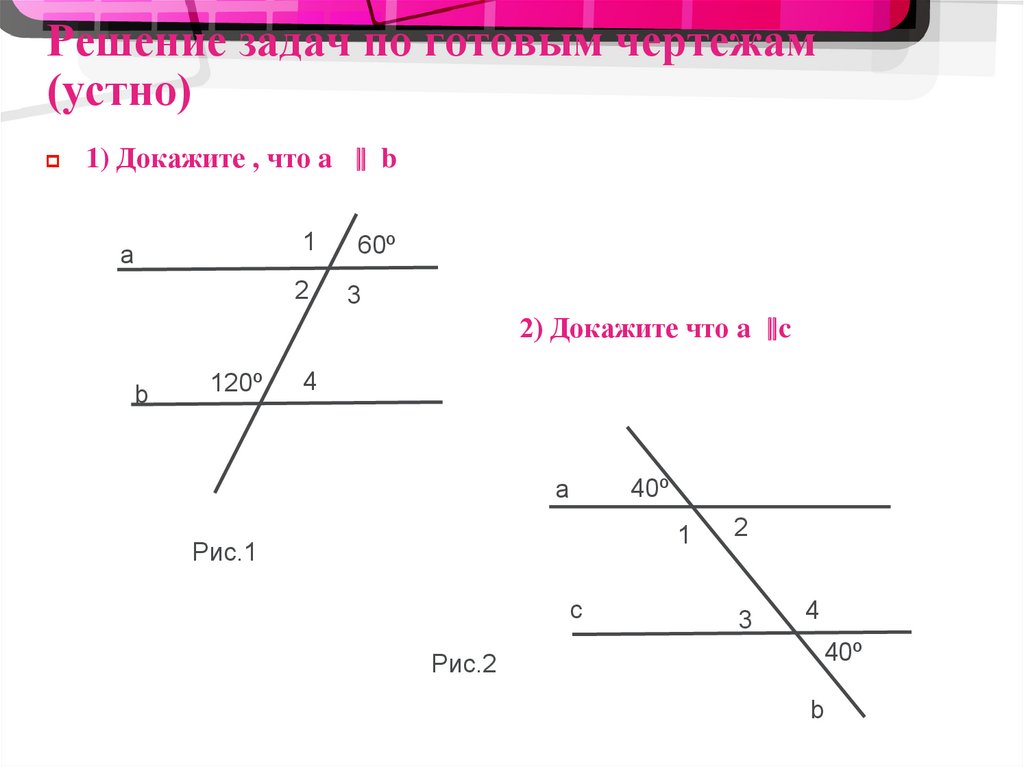
2. Решение задач по готовым чертежам (устно)

1) Докажите , что a ∥ b
1
a
2
60º
3
2) Докажите что a ∥c
b
120º
4
40º
a
1
Рис.1
c
Рис.2
2
3
4
40º
b

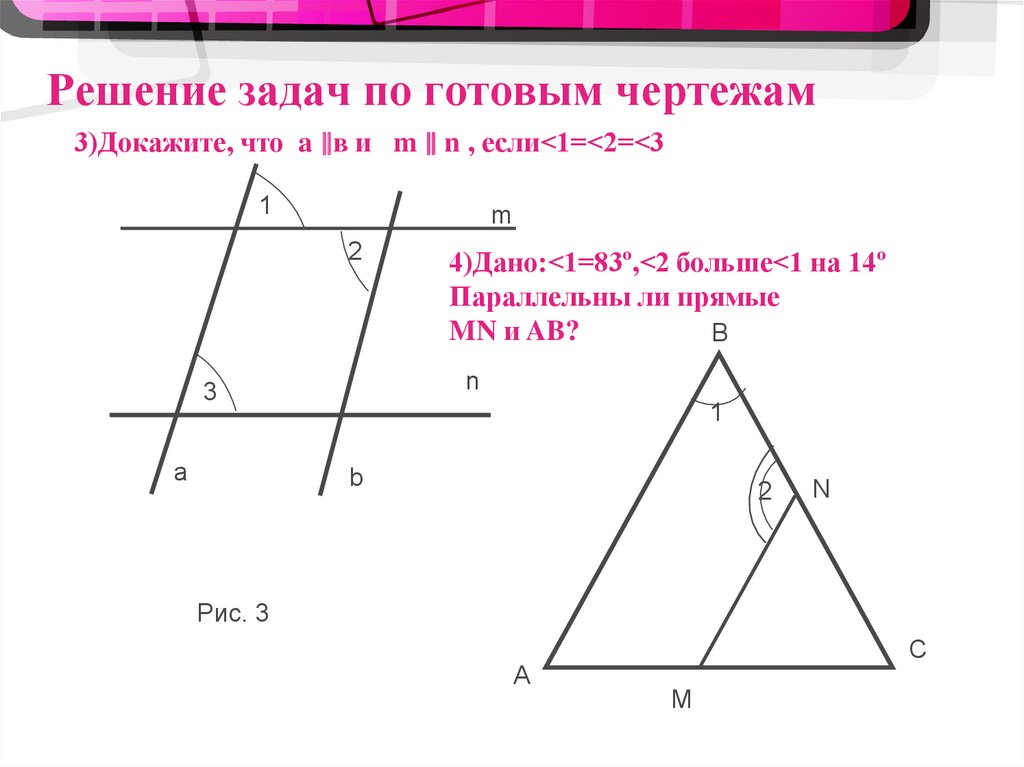
3. Решение задач по готовым чертежам

3)Докажите, что a ∥в и m ∥ n , если<1=<2=<3
1
m
2
n
3
a
4)Дано:<1=83º,<2 больше<1 на 14º
Параллельны ли прямые
MN и AB?
B
1
b
2
N
Рис. 3
C
A
M

4. Решить задачу по рисунку

В
№190
На рисунке 1 АВ=ВС, АD=DE,
<C=70º <EAC=35º.
Докажите, чтоDE∥AC.
D
A
E
35º
Рис .1
70º
C

5. Проверь себя

Дано:AB=BC, AD=DE ,<C=70º ,< EAC=35º
Доказать:DE∥EC
Доказательство:
1)Так какAB=AC, то<A=<C=70º( свойство равнобедренного
треугольника.)
2) Так как<EAC=35º,<A=70º,то<DAE=35º
3)Так как△ADE-равнобедренный, то <DAE=<DEA=35º( по
свойству).
4)<DEA=<EAC=35º <DEA и<EAC -накрест лежащие при
прямых DE и AC и секущей AE. DE∥AC.
Что и требовалось доказать.

6. Решение задач

№213
На рис.2
B
C
CE=ED, BE=EF, KE∥AD.
Докажите, что
KE∥BC
1
K
E
2
A
D
Рис.2
F

7. Проверь себя

Дано: CE=ED,BE=EF,KE∥AD.
Доказать:KE∥BC.
Доказательство:
1) Рассмотрим △BCF и△FDE
BE=EF( по усл.), тогда△BCE=△FDE
(по двум сторонам и углу между ними).<CBE=<DFE( по
определению равных треугольников).
2)<CBE=<DFE- накрест лежащие при прямыхBC иAD и
секущей BF,<CBE=<DFE( по п.1),тогдаBC∥AD по
признаку.
3)KE∥AD( по усл.),BC∥AD( из п.2),тогдаKE∥BC( свойство
параллельных прямых), что и требовалось доказать.

8. Самостоятельная работа

1 вариант
1.Параллельны ли прямые d и e ,
изображенные на рис.1?
2.На рис.2 точкаО-середина отрезков
EL и KF.Докажите,чтоEF∥KL
2 вариант
1.Параллельны ли прямые m иn,
изображенные на рис.3?
2.На рис.4 точкаF-середина отрезков
MO и NP. Докажите,что MN∥PO.

9. Домашнее задание

Повторить материал пунктов 24-26;
Решить задач:и №214,№216
Спасибо за урок!