Похожие презентации:
Решение задач С2 методом координат
1. Решение задач С2 методом координат
Дорофеева Лилия Ильиничнаучитель математики
МБОУ СОШ №6, г.Нижнекамск
Республики Татарстан
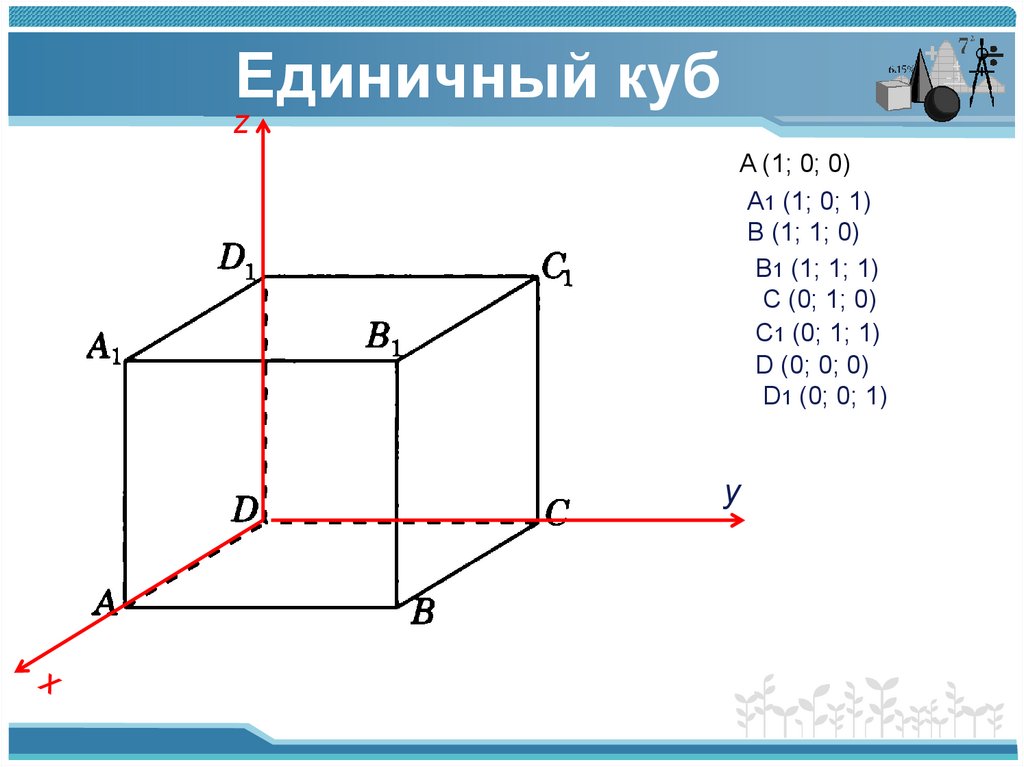
2. Единичный куб
zA (1; 0; 0)
A1 (1; 0; 1)
B (1; 1; 0)
B1 (1; 1; 1)
C (0; 1; 0)
C1 (0; 1; 1)
D (0; 0; 0)
D1 (0; 0; 1)
y
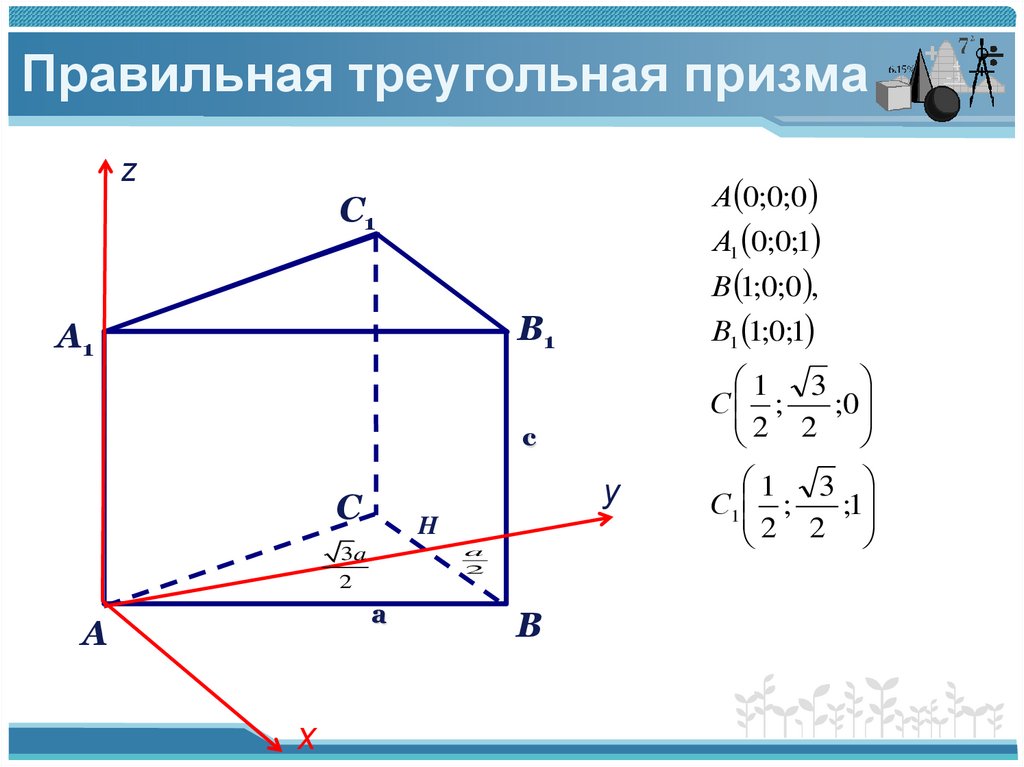
3. Правильная треугольная призма
zС1
3a
B 0;
; 0
2
В1
a
C ;0;0
2
А1
a
2
А
х
a
A ;0;0
2
С
O
c
3a
2
a
В
у
a
A1 ;0; c
2
3a
B1 0;
; c
2
a
C1 ;0; c
2
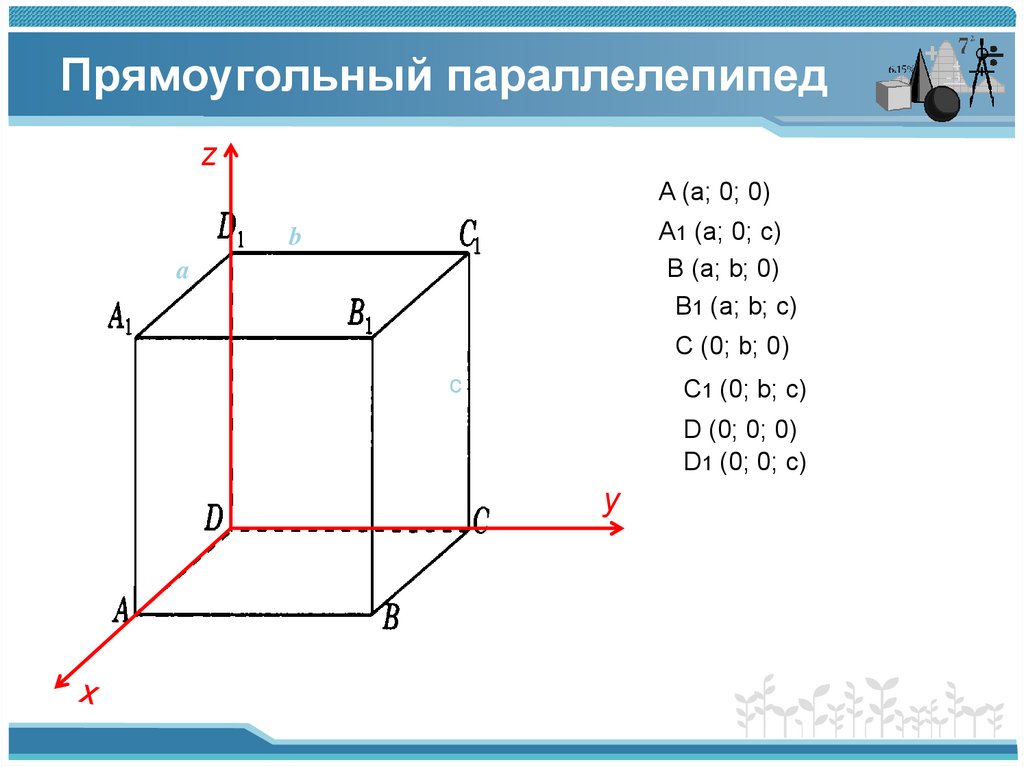
4. Прямоугольный параллелепипед
zA (a; 0; 0)
A1 (a; 0; c)
B (a; b; 0)
B1 (a; b; c)
b
a
C (0; b; 0)
с
C1 (0; b; c)
D (0; 0; 0)
D1 (0; 0; c)
y
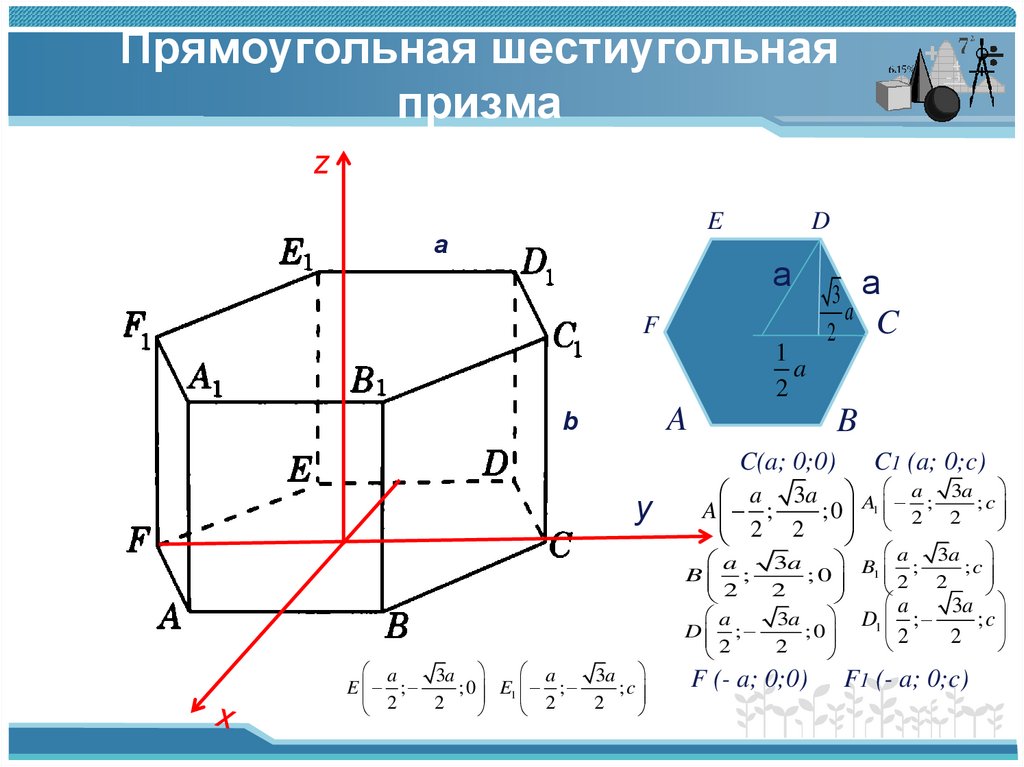
5. Прямоугольная шестиугольная призма
zE
D
a
a
F
1
a
2
3 a
a
C
2
A
b
B
C(a; 0;0)
y
a
a
3a
3a
E ;
; 0 E1 ;
; c
2
2
2
2
C1 (a; 0;c)
a 3a A a ; 3a ; c
A ;
;0 1 2 2
2 2
a
B a ; 3a ; c
3a
1
B
2 ; 2 ;0
2 2
a
3
a
a
3a D1 ;
;
c
2
D ;
; 0
2
2
2
F (- a; 0;0) F1 (- a; 0;c)
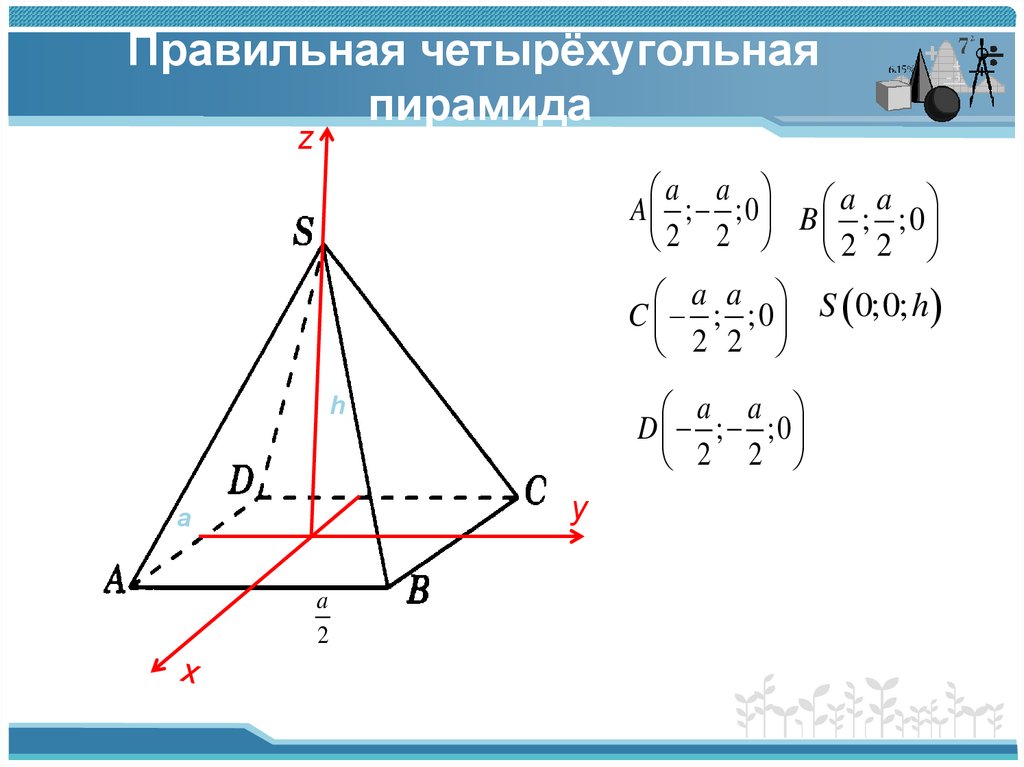
6. Правильная четырёхугольная пирамида
za a
A ; ;0 B a ; a ;0
2 2
2 2
a a S 0;0; h
C ; ;0
2 2
a a
D ; ;0
2 2
h
y
a
a
2
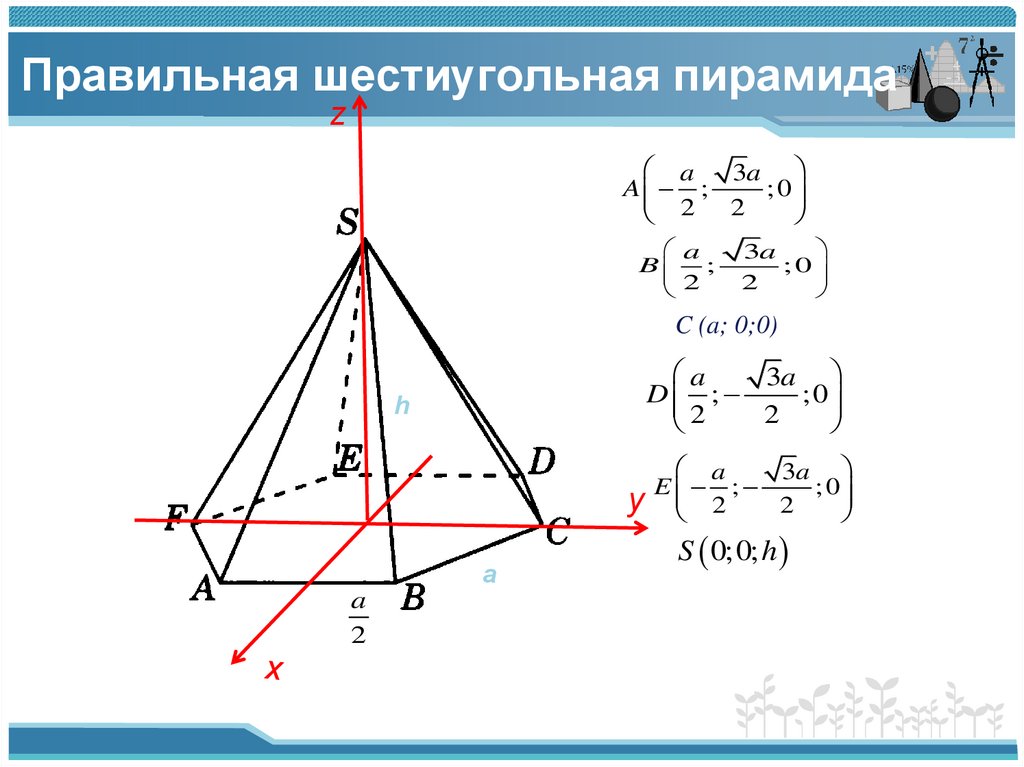
7. Правильная шестиугольная пирамида
za
3a
A ;
; 0
2
2
a
B
2;
3a
;0
2
C (a; 0;0)
a
3a
D ;
; 0
2
2
h
y
a
a
2
a
3a
E ;
; 0
2
2
S 0;0; h
8. Правильная треугольная призма
zА 0;0;0
С1
А1 0;0;1
В 1;0;0 ,
А1
С
3a
2
В1
В1 1;0;1
с
1 3
С ;
;0
2 2
у
H
a
2
В
А
х
1 3
С1 ;
;1
2 2
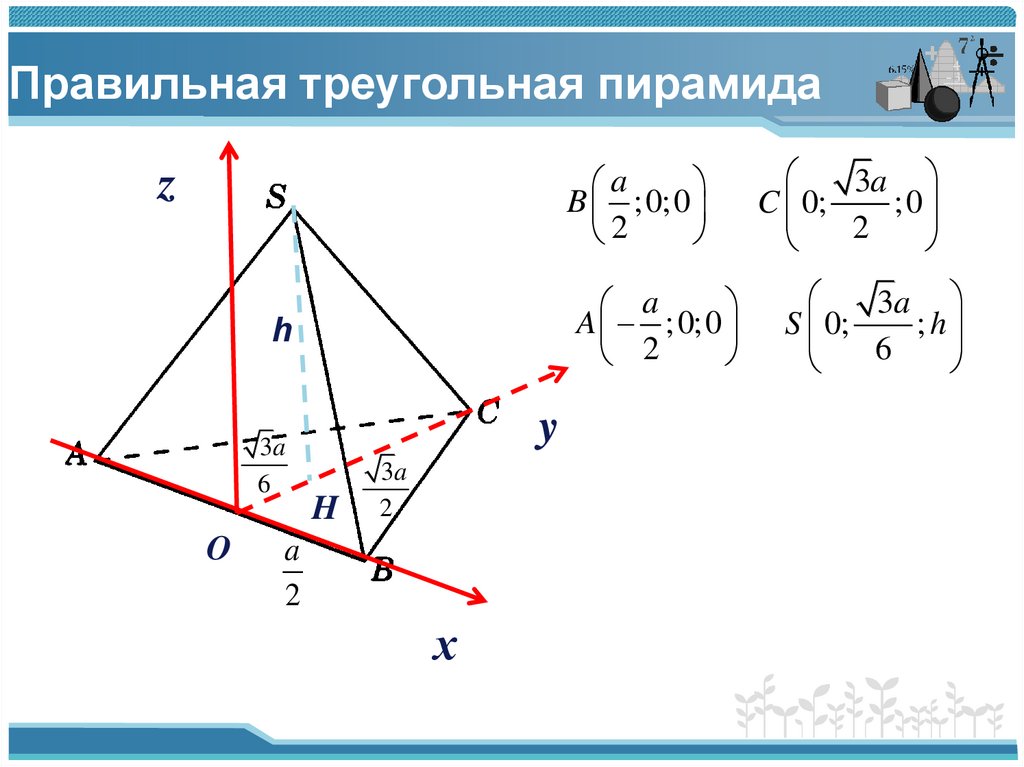
9. Правильная треугольная пирамида
aB ;0;0
2
z
a
A ;0;0
2
h
3a
6
O
y
H
3a
2
a
2
х
3a
C 0;
;0
2
3a
S 0;
; h
6
10. Угол между прямой и плоскостью
Прямая а образуетс плоскостью угол 90 . Плоскость задана
уравнением: ах+ву+сz+d=0 и n а; в; с - вектор нормали,
Синус угла определяется по формуле:
sin
xа а у а в z а с
ха у а z а а 2 в 2 с 2
2
2
2
11. Угол между прямыми
Вектор а ха ; уа ; z а лежит на прямой а, Векторпрямой в.
Косинус угла между прямыми а и в:
cos
в хв ; ув ; z в лежит на
x а xв у а у в z а z в
х а у а z а хв у в z в
2
2
2
2
2
2
12. Угол между плоскостями
1.3. Угол между двумя плоскостями. Плоскость заданауравнением: а1 х в1 у с1 z d 0 и ее вектор нормали n а1 ; в1 ; с1
плоскость задана уравнением а2 х в2 у с2 z d 0 и ее вектор
нормали n а 2 ; в 2 ; с 2 . Косинус угла между плоскостями:
cos
а1 а2 в1 в 2 с1 с2
а1 в1 с1 а2 в 2 с2
2
2
2
2
2
2
13. Расстояние от точки до плоскости
Расстояние h от точки М xМ ; уМ ; z М до плоскости , заданнойуравнением ах+ву+сz+d=0 определяется по формуле:
h
а хМ в у М с z М d
а в с
2
2
2
14.
Примеры решения задачz
АВ1 ВС1
1. В единичном кубе найти угол между прямыми
и
Введем систему координат и найдем координаты
точек А, В, В1 , С1
A (0; 0; 0), B (1; 0; 0) , B1 (1; 0; 1) , C1 (1; 1; 1)
Находим координаты направляющих векторов
прямых АВ1 и ВС1 по формуле 1.
y
АВ1 1;0;1 , ВС1 0;1;0
х
Косинус угла между прямыми АВ1 и ВС 1 определяется по формуле 1.1:
cos
1 0 0 1 1 1
12 12 12 12
Ответ : 60
1
, 60
2
15.
2.В правильной шестиугольной призме А...F1, все ребра которойравны 1, найти угол между прямой AF и плоскостью ВСС1
Введем систему координат и находим координаты
нужных точек.
1 3
;0
2
2
z
Найдем координаты вектора AF - ;
Плоскость ВСС1 совпадает с плоскостью грани
ВВ1С1С ; зададим ее с помощью точек
y
3 3
В 1;0;0 , В1 1;0;1 , С ;
;0
2 2
Пусть ax+by+cz+d=0 – уравнение плоскости ВСС1
В 1;0;0 ВСС1 а d 0
d -a
х
c 0
B 1;0;1 ВСС1 a с d 0
1
a
3 3
3
3
b
С ; ;0 ВСС1 а b
d 0
3
2
2
2
2
Уравнение плоскости ВСС1 примет вид aх - а у а 0или 3х у 3 0
3
Вектор нормали : n 3; 1;0
Синус искомого угла:
sin
3
1
3 1
0 0
2
2
3
2
2
2
1 3
2
1 0
0
2
2
3
; Ответ : 60
2
16.
3.В правильной четырехугольной пирамиде , все ребра которойравны 1, найти синус угла между прямой ВЕ и плоскостью SAD,
где Е- середина ребра SC
Координаты точки Е определим по формуле 3:
z
3 3 2
1 3 2
и ВЕ ; ;
Е ; ;
4
4
4
4
4
4
Пусть уравнение плоскости ADS ax+by+cz+d=0
y
Из того, что А 0;0;0 , D 0;1;0 S 1 ; 1 ; 2 ADS
2 2 2
2
х
1
1
d 0
следует, что d=0, b+d=0 и : а b c
2
2
2
Отсюда получим, что а 2с, b 0, d 0 и уравнение плоскости ADS примет вид:
2сх сz 0, или 2 х z 0 . Вектор нормали n 2 ;0; 1
Синус угла между прямой ВЕ плоскостью ADS определим по формуле 1.2
sin
3
2
1
2 - 0 1
4
4
4
2
2
2
2
1
3
4
4
4
2
2
0 2 12
2
3
Ответ :
2
3
17.
4.В единичном кубе А… D1 ,найти расстояние от точки А доВD1
прямой
Находим координаты точек А 0;0;0 В 1;0;0 D1 0;1;1 , вектора ВD 1 1;1;1
Искомое расстояние есть длина перпендикуляра АК.
Если отрезок ВD разделен точкой K(x;y;z) в отношении λ ,
то координаты точки К определяются по формуле 1.5:
z
y
К
х
х
1 0
0
0 1 0 0 0
1 0 0 0
;у
;z
K
;
;
;
;
АК
1
1
1 1 1 1
1 1 1
т.к. АК ВD1 AK BD1 0
1
1
2 1 1
2 1 1
0 K ; ; , AK ; ;
1 1 1
2
3 3 3
3 3 3
AK
4 1 1
9 9 9
6
6
9
3
Ответ :
6
3
18.
5.В правильной шестиугольной призме А...F1 , все ребра которойравны 1, найти расстояние от точки А до плоскости BFE1
z
1 3
Координаты точек А 0;0;0 В 1;0;0 и Е1 0; 3;1 , F - ;
;0
2 2
Подставив координаты точек B, F и E в общее уравнение
1
плоскости получим систему уравнений:
3
1
В ВFE1 a b
d 0
2
2
y
1 3
3
1
F ;
;0 ВFE1 a b
d 0
2
2
2 2
х
E 0; 3;1 BFE1 b 3 c 1 d 0
1
Откуда d -a, c -2a, b a 3
Уравнение плоскости примет вид: ax 3ay 2az a 0, или x 3 y 2 z 1 0
Вектор нормали: n 1; 3; 2
Вычислим расстояние h от точки А до плоскости BFE по формуле 1.4:
h
1 0 3 0 2 0 1
12
3
2
2
2
1
2
4
Ответ :
2
4
1
8
19.
6.В единичном кубе А...D , найти расстояние между1
прямыми АВ1 и ВС1
При параллельном переносе на вектор ВА прямая ВС
1
отображается на прямую АD . Таким образом, плос1
кость AB D содержит прямую АВ и параллельна
1 1
1
прямой ВС . Расстояние между прямыми АВ1 и ВС1
1
находим как расстояние от точки В до плоскости AB1D1
z
y
х
Пусть ax+by+cz+d=0 – уравнение плоскости AB D .
1 1
Так как А 0;0;0 АВ1D1 d 0
B 1;0;1 AB1D1 a c
1
D 0;1;1 A1B1D1 b c
1
Уравнение плоскости запишется как –сx-сy+cz=0, или х+у+z=0..
Вектор нормали n 1;1; 1
Расстояние h от точки B 1;0;0 до плоскости AB D находим по формуле
1 1
1 1 1 0 1 0
1
3
h
2
3
3
12 12 1
Ответ :
3
3
20.
Литература:1.Каталог задач: www.problems.ru
2.Образовательный портал»Физ/мат класс»: www.fmclass.ru
3.Открытый банк задач: www.mathege.ru
4.Федеральный институт педагогических измерений: www.fipi.ru













 Математика
Математика








