Метод координат при решении стереометрических задач. Урок геометрии, 11 класс

1. Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №3 г.Козьмодемьянска Метод координат при решении

стереометрических задач
урок геометрии, 11 класс
Автор: Уртюкова Мая Андреевна,
учитель математики

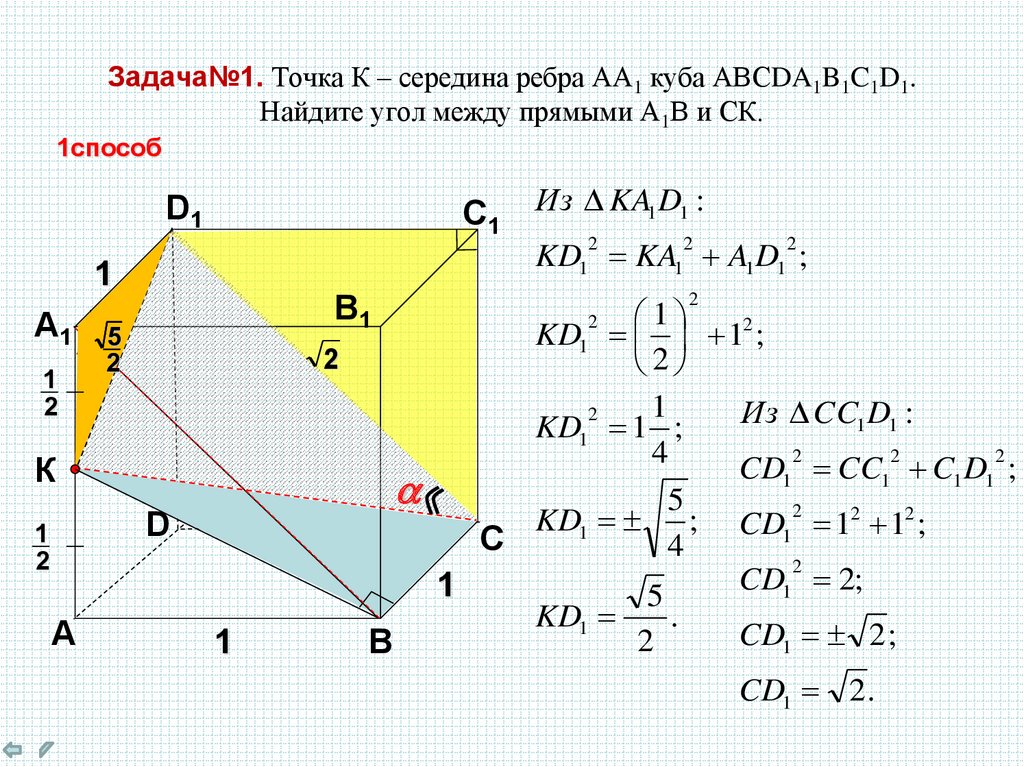
2. Задача№1. Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.

1способ
С1
D1
1
А1
1
2
В1
5
2
a
D
1
2
А
1
В
KD1 KA1 A1 D1 ;
2
2
2
2
2
К
Из KA1 D1 :
1
2
KD1 12 ;
2
1
2
Из CC1 D1 :
KD1 1 ;
2
2
2
4
CD1 CC1 C1 D1 ;
5
KD1 ; CD12 12 12 ;
С
4
2
CD
1
1 2;
5
KD1
.
CD1 2 ;
2
CD1 2 .

3.

Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол
между прямыми А1В и СК.
Из треугольника
KBC
D1
С1Составляем теорему косинусов для
стороны KD1:
1
А1
1
2
5
2
5 3 2
2 2
2
3
2
D
А
2
В1
К
1
2
3
KC
2
a
5
2
1
1
В
2 2 32
2
1
3 2 cos a 3
С
cos a
cos a
3
3 2
2
2
a 450
2 cos a

4. Угол между прямыми

а
р
q
b
р
- направляющий вектор прямой а
q
- направляющий вектор прямой b
- угол между прямыми
p x1 ; y1 ; z1
cos =
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22

5.

Задача№1. Точка К – середина ребра АА1 единичного куба
АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
2 способ
x x y y z z
1
2
1
2
1
2
BA1{z0; 1;1}; KC{ 1;1; 1 } cos
2
2
2
2
2
2
2
x
y
z
x
y
z
1
1
1
2
2
2
D1
С
1
1
(1;0;1)
А1?
В1
cos
1
0 1 1 1 1
2
1
2
2
0 2 1 12 1 12
2
1
(1;0; 2 )
К?
С(?0;1;0)
cos
D
1
х
А
1
1
?
В(1;1;0)
1
1
2
1
2 2
4
2
cos
2
3
2
9
2
4
3
2
2
450
3
2
2

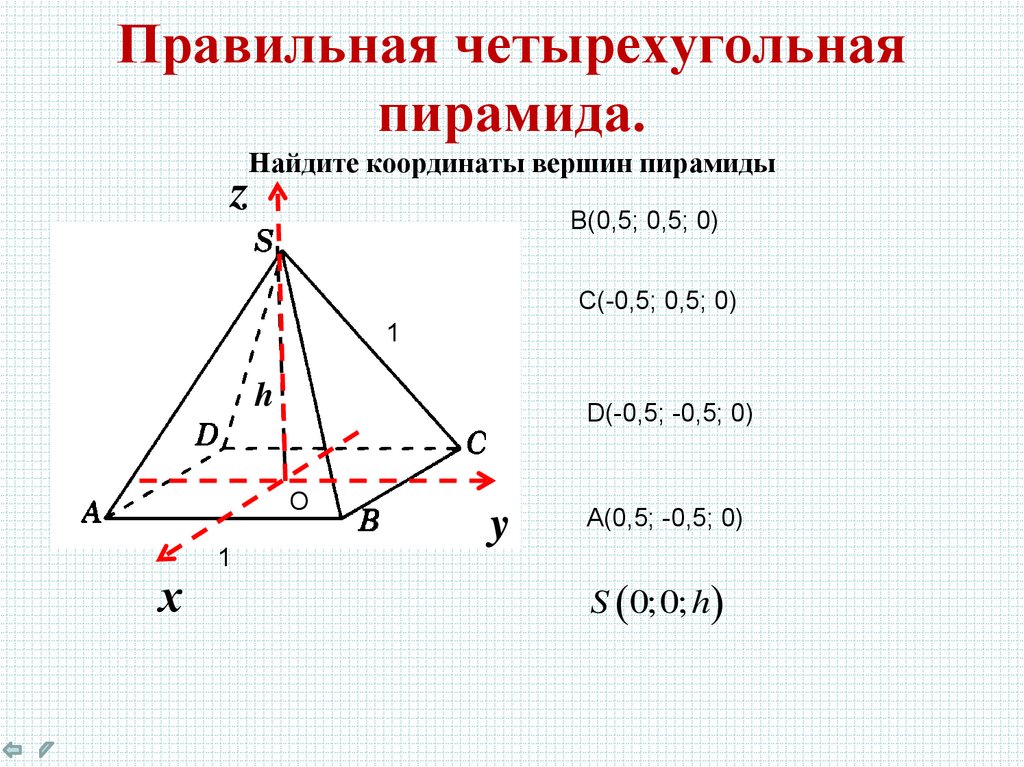
6. Правильная четырехугольная пирамида. Найдите координаты вершин пирамиды

z
B(0,5; 0,5; 0)
С(-0,5; 0,5; 0)
1
h
h
D(-0,5; -0,5; 0)
О
х
1
y
А(0,5; -0,5; 0)
S 0;0; h

7.

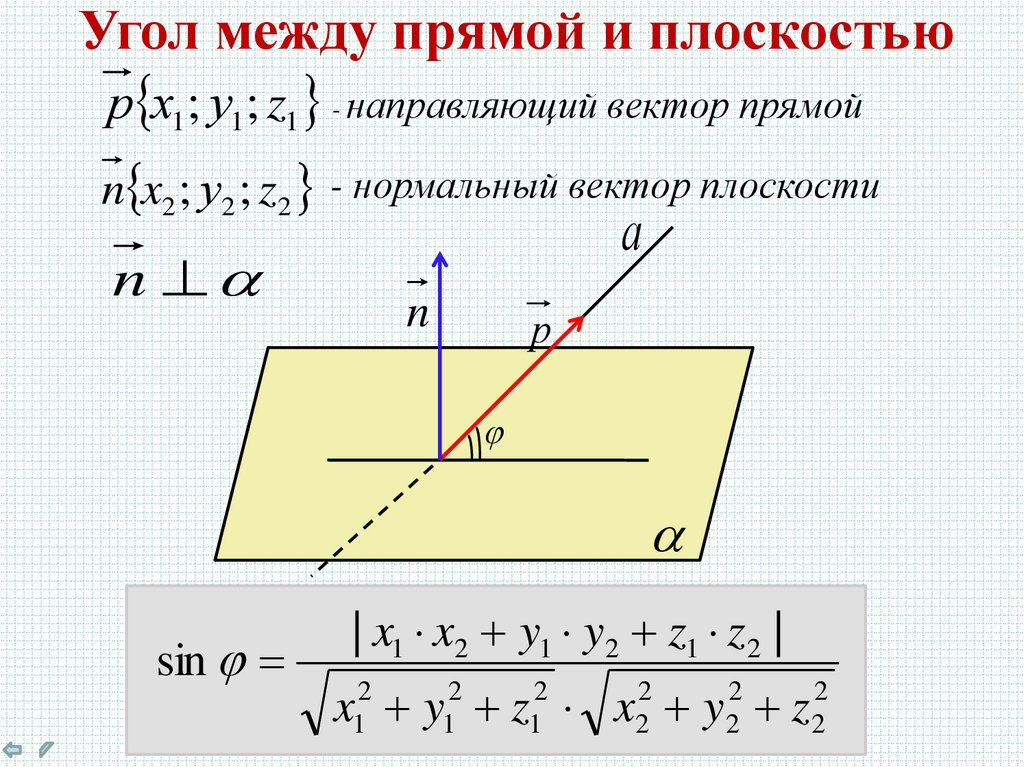
Угол между прямой и плоскостью
р х1; у1; z1 - направляющий вектор прямой
n x2 ; у2 ; z2 - нормальный вектор плоскости
а
n a
n
р
a
sin
| x1 x2 y1 y2 z1 z 2 |
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2

8.

Задача 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1
(АВ = AD = 2, АА1 = 1). Найти угол между прямой АС1 и плоскостью АВ1С.
C1
z
D1
B1
C (0;0;0), A(2;2;0) C1 0;0;1 B1 0;2;1
x y 2 z 0 n 1; 1;2
A1
C
B
у
D
A
х
Ответ:
6
arcsin
9
sin AC1 ; AB1C cos AC1 ; n
2 2 2
6
9
4 4 1 1 1 4

9.

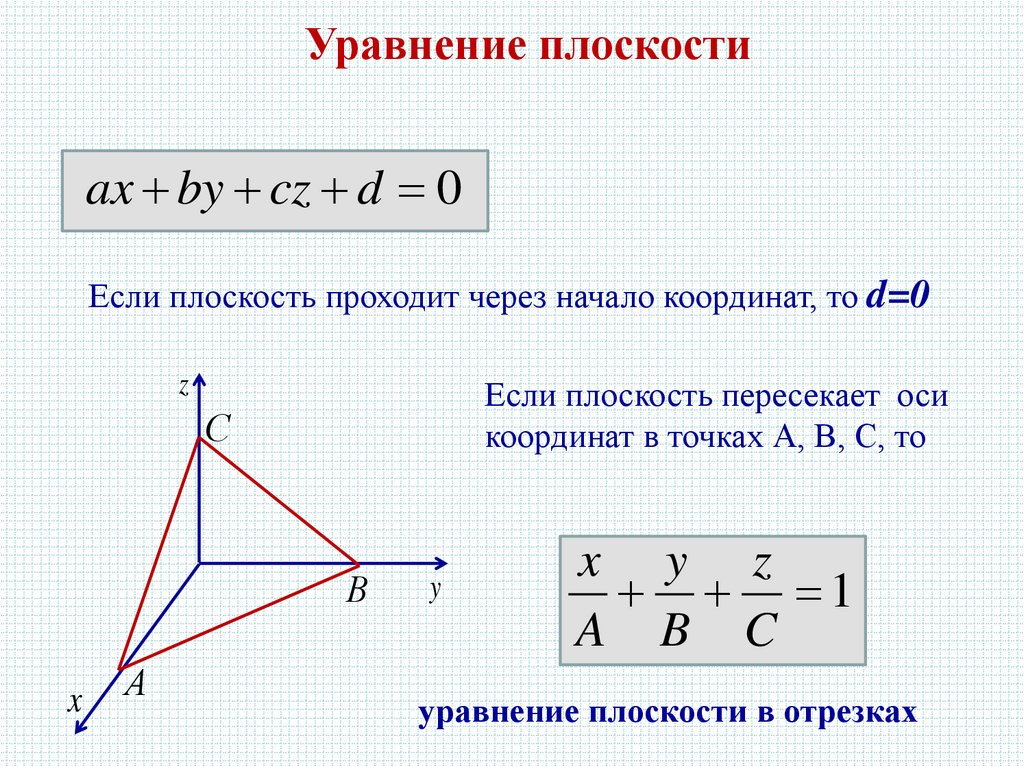
Уравнение плоскости
ax by cz d 0
Если плоскость проходит через начало координат, то d=0
z
Если плоскость пересекает оси
координат в точках А, В, С, то
С
В
x
А
y
x y z
1
A B C
уравнение плоскости в отрезках

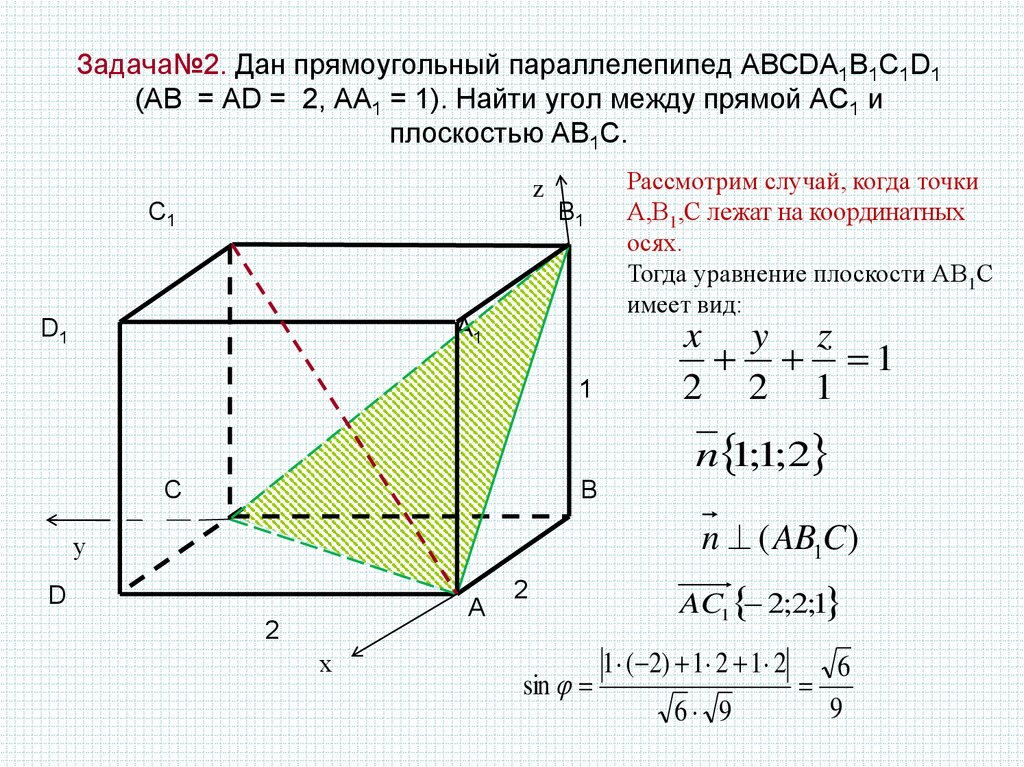
10. Задача№2. Дан прямоугольный параллелепипед АВСDA1B1C1D1 (АВ = AD = 2, АА1 = 1). Найти угол между прямой АС1 и плоскостью АВ1С.

z
C1
D1
B1
A1
1
Рассмотрим случай, когда точки
А,В1,С лежат на координатных
осях.
Тогда уравнение плоскости АВ1С
имеет вид:
x y z
1
2 2 1
n 1;1;2
C
B
n ( AB1C )
у
D
A
2
х
2
sin
AC1 2;2;1
1 ( 2) 1 2 1 2
6 9
6
9

11.

Угол между плоскостями
a : a1x b1 y c1z d1 0
Вектор нормали плоскости a : n1{a1 ; b1 ; c1}
: a2 x b2 y c2 z d2 0
Вектор нормали плоскости : n2 {a2 ; b2 ; c2 }
cos
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
2
2
2

12.

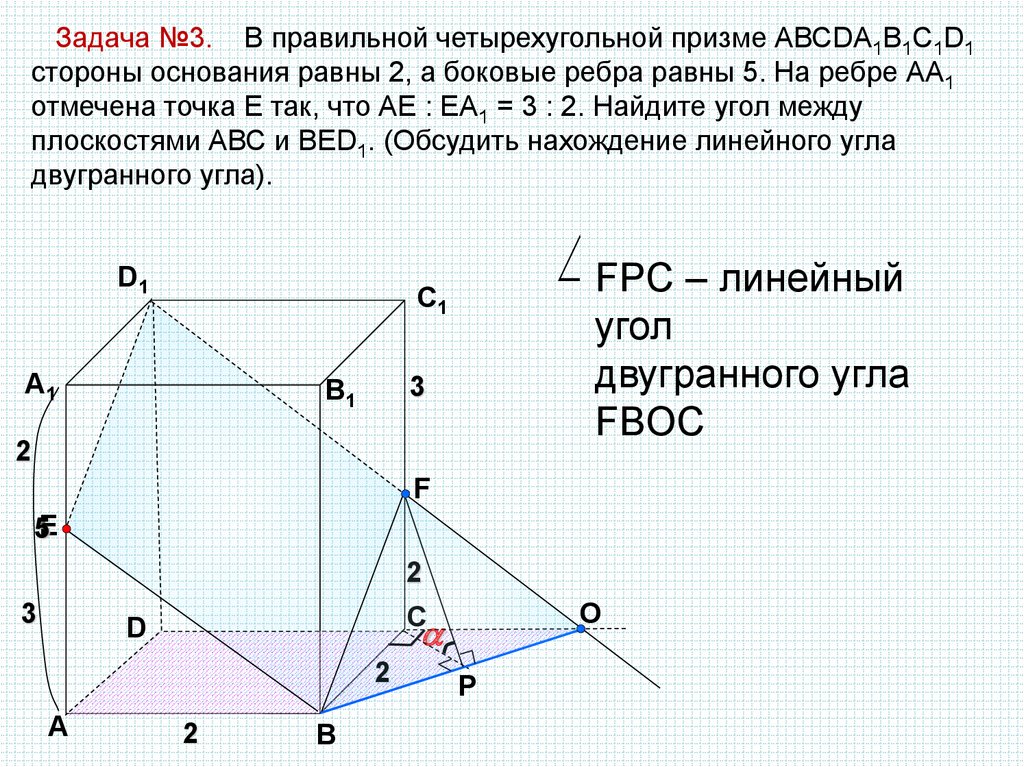
Задача №3. В правильной четырехугольной призме АВСDA1B1C1D1
стороны основания равны 2, а боковые ребра равны 5. На ребре АА1
отмечена точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между
плоскостями АВС и ВЕD1. (Обсудить нахождение линейного угла
двугранного угла).
D1
FPC – линейный
C1
A1
угол
двугранного угла
FBOC
3
B1
2
F
5E
2
3
a
2
А
O
C
D
2
В
P

13.

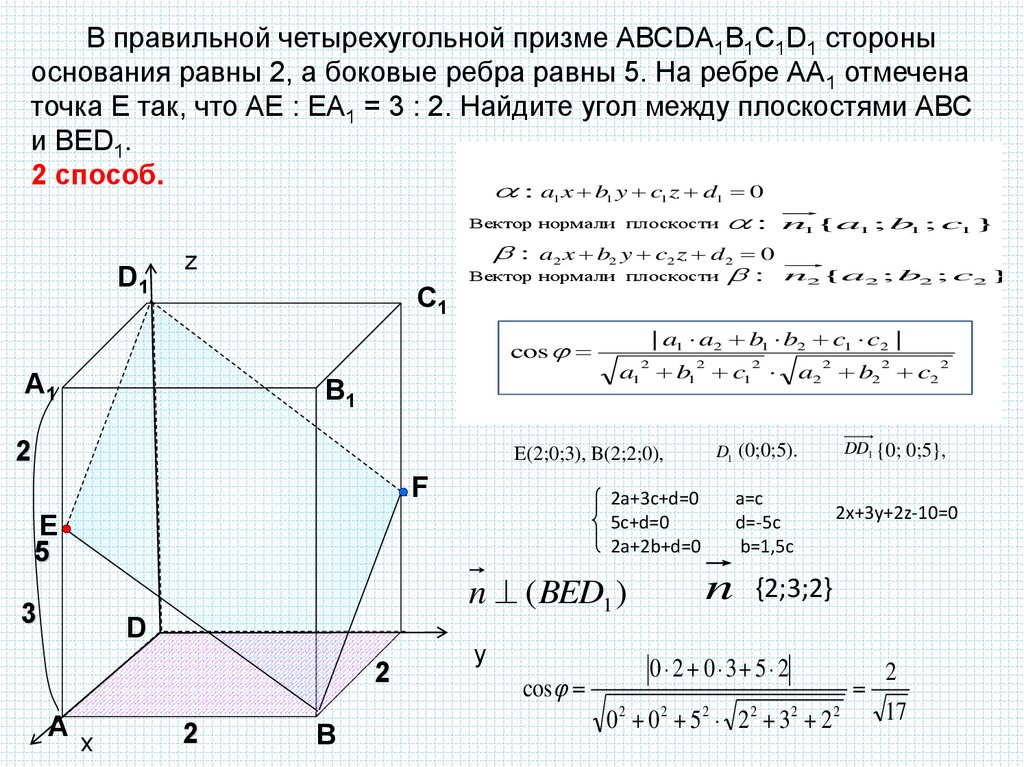
В правильной четырехугольной призме АВСDA1B1C1D1 стороны
основания равны 2, а боковые ребра равны 5. На ребре АА1 отмечена
точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между плоскостями АВС
и ВЕD1.
2 способ.
a : a x b y c z d 0
1
1
1
1
Вектор нормали плоскости
D1
:
z
n1{a1 ; b1 ; c1}
a2 x b2 y c2 z d 2 0
Вектор нормали плоскости
:
n2 {a2 ; b2 ; c2 }
C1
cos
A1
B1
2
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1
2
2
E(2;0;3), B(2;2;0),
F
2
n ( BED1 )
a2 b2 c2
2
2
a=c
d=-5c
b=1,5c
n
2x+3y+2z-10=0
{2;3;2}
D
2
А
x
2
В
y
cos
2
DD1 {0; 0;5},
D1 (0;0;5).
2a+3c+d=0
5c+d=0
2a+2b+d=0
E
5
3
a:
0 2 0 3 5 2
0 2 0 2 5 2 2 2 32 2 2
2
17

14.

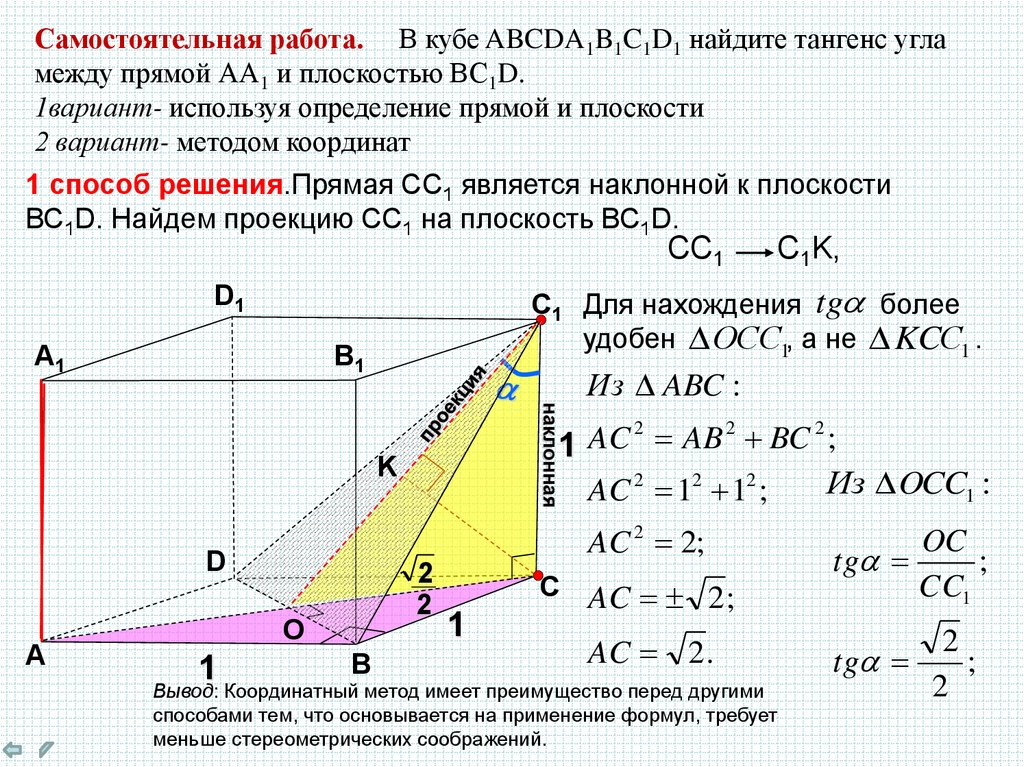
Самостоятельная работа. В кубе ABCDA1B1C1D1 найдите тангенс угла
между прямой АА1 и плоскостью ВС1D.
1вариант- используя определение прямой и плоскости
2 вариант- методом координат
1 способ решения.Прямая СС1 является наклонной к плоскости
ВС1D. Найдем проекцию СС1 на плоскость ВС1D.
СC1
С1 Для нахождения tga более
удобен ОСС1, а не KCС1 .
D1
А1
В1
наклонная
AC 2 2;
D
2
2
О
1
Из ABC :
2
2
2
AC
AB
BC
;
1
Из OCC1 :
AC 2 12 12 ;
K
А
C1K,
В
1
С AC 2 ;
AC 2 .
Вывод: Координатный метод имеет преимущество перед другими
способами тем, что основывается на применение формул, требует
меньше стереометрических соображений.
OC
tga
;
CC1
tga
2
;
2

15. Домашнее задание

В кубе ABCD