Похожие презентации:
Аксиомы стереометрии. Некоторые следствия из аксиом
1.
Аксиомыстереометрии
Некоторые
следствия
из аксиом
2. Геометрия
ПланиметрияСтереометрия
Stereos:
телесный, твердый,
объемный,
пространственный
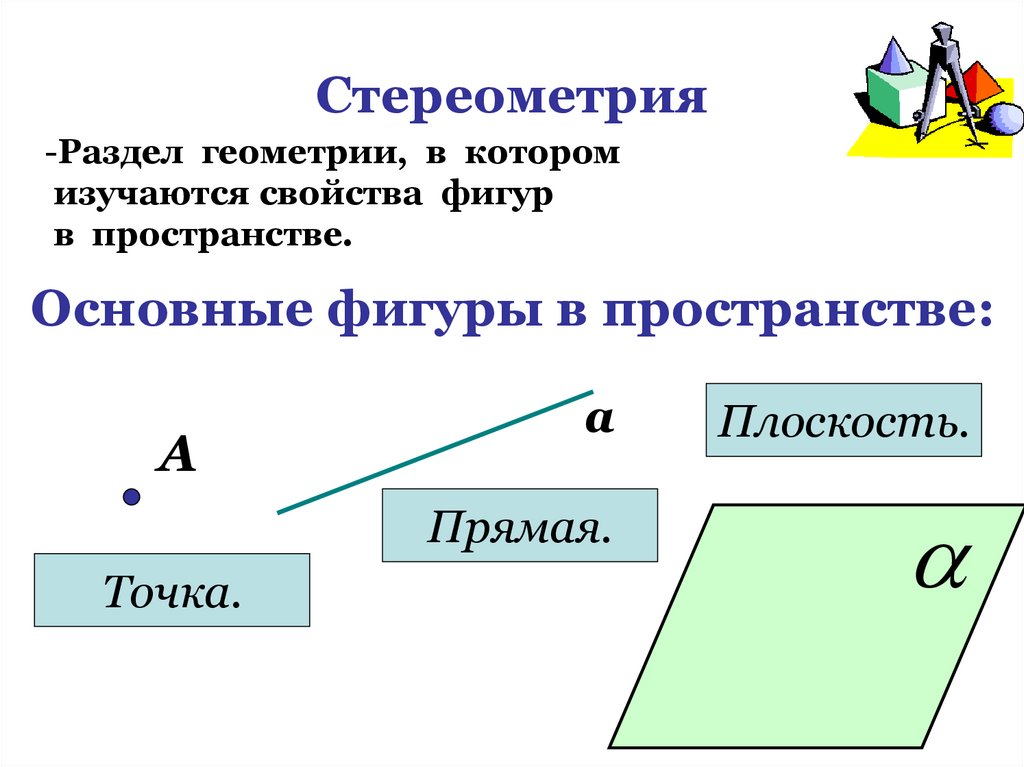
3. Стереометрия
-Раздел геометрии, в которомизучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Плоскость.
Прямая.
4.
A, B, C, …a, b, c, …
или
AВ, BС, CD, …
, , ,
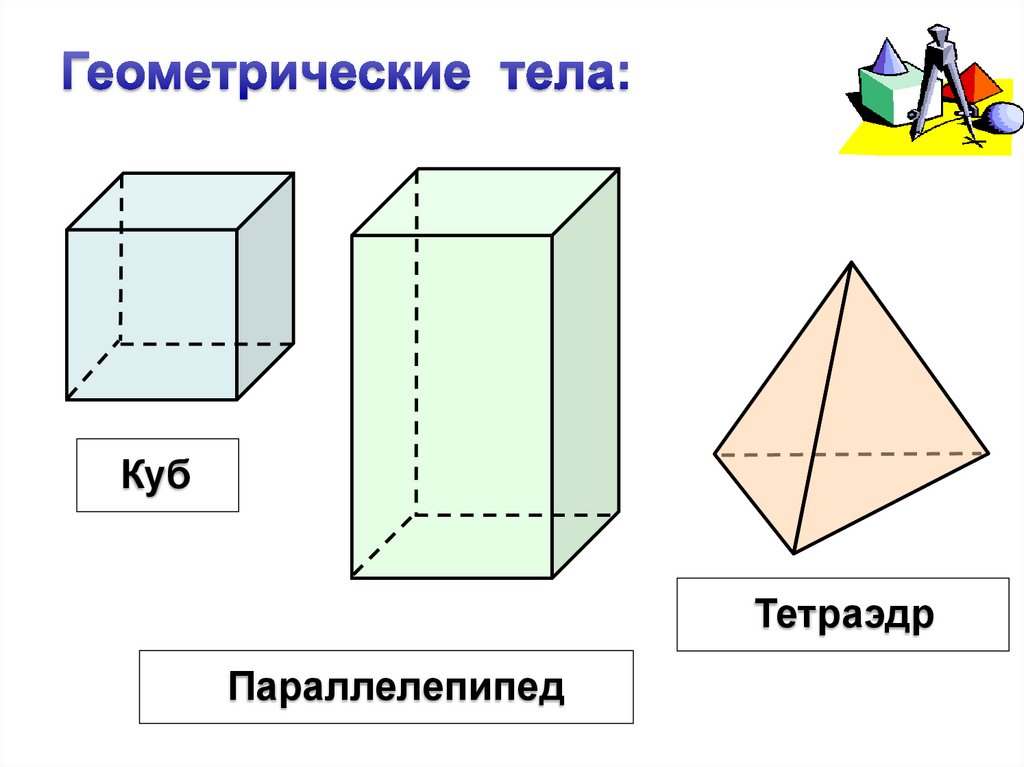
5. Геометрические тела:
КубТетраэдр
Параллелепипед
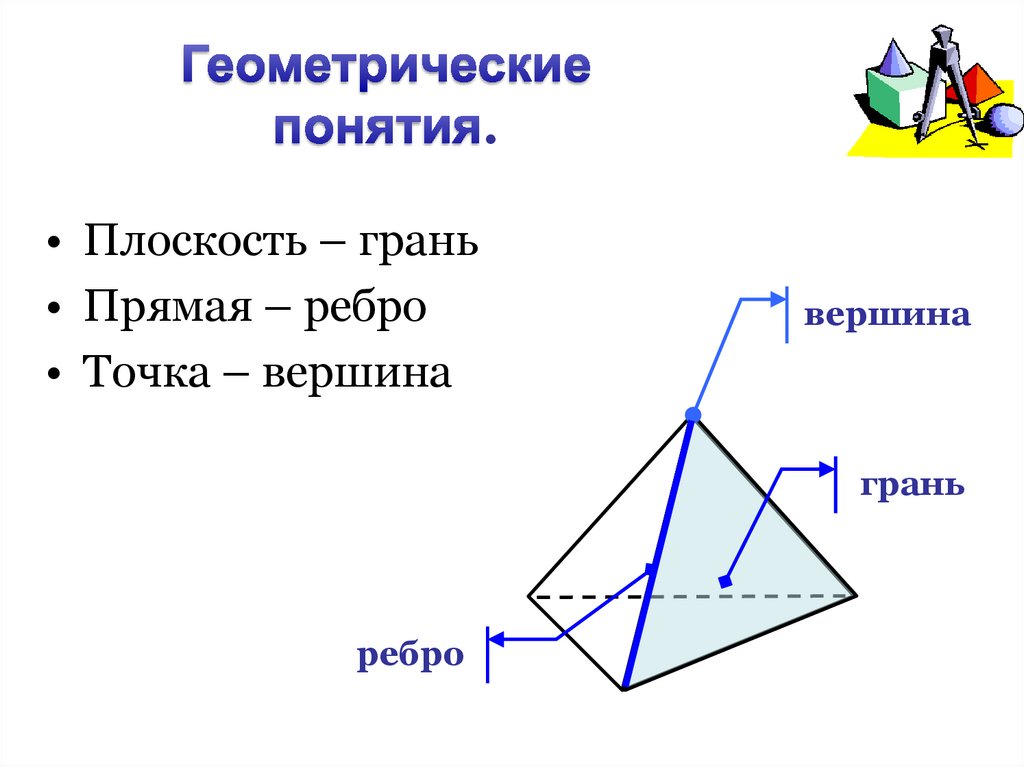
6. Геометрические понятия.
.• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро
7. Аксиома
(от греч. axíõma – принятие положения)8.
Характеризуют взаимноерасположение точек и прямых
1. Каждой прямой
принадлежат по крайней
мере две точки
2. Имеются по крайней мере три
точки, не лежащие на одной
прямой
3. Через любые две точки
проходит прямая, и притом только
одна.
Основное понятие геометрии
«лежать между»
4. Из трех точек прямой одна и
только одна лежит между двумя
другими.
А1. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
А2. Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости
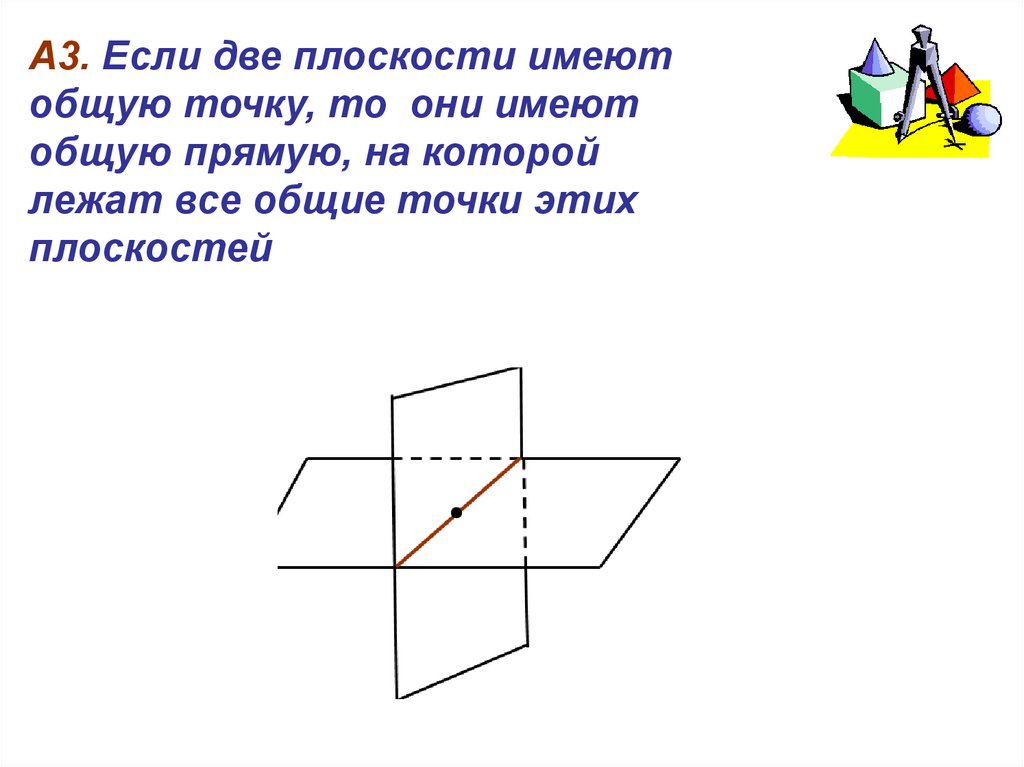
А3. Если две плоскости имеют
общую точку, то они имеют
общую прямую, на которой
лежат все общие точки этих
плоскостей.
9.
А3. Если две плоскости имеютобщую точку, то они имеют
общую прямую, на которой
лежат все общие точки этих
плоскостей
10.
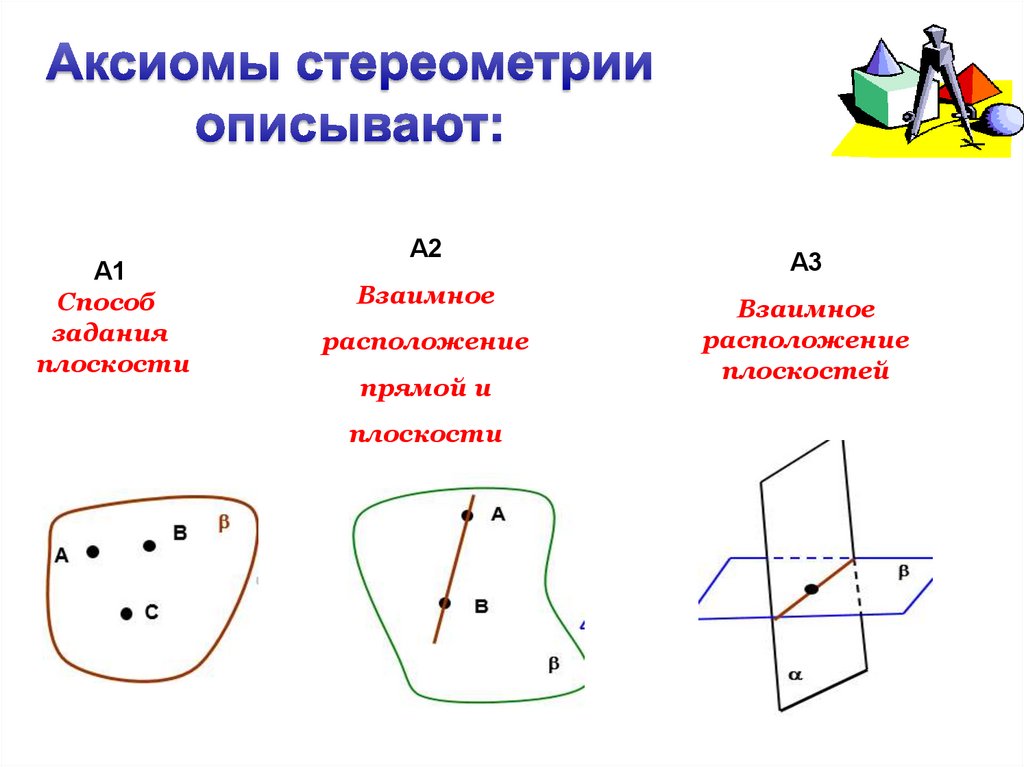
А1Способ
задания
плоскости
А2
Взаимное
расположение
прямой и
плоскости
А3
Взаимное
расположение
плоскостей
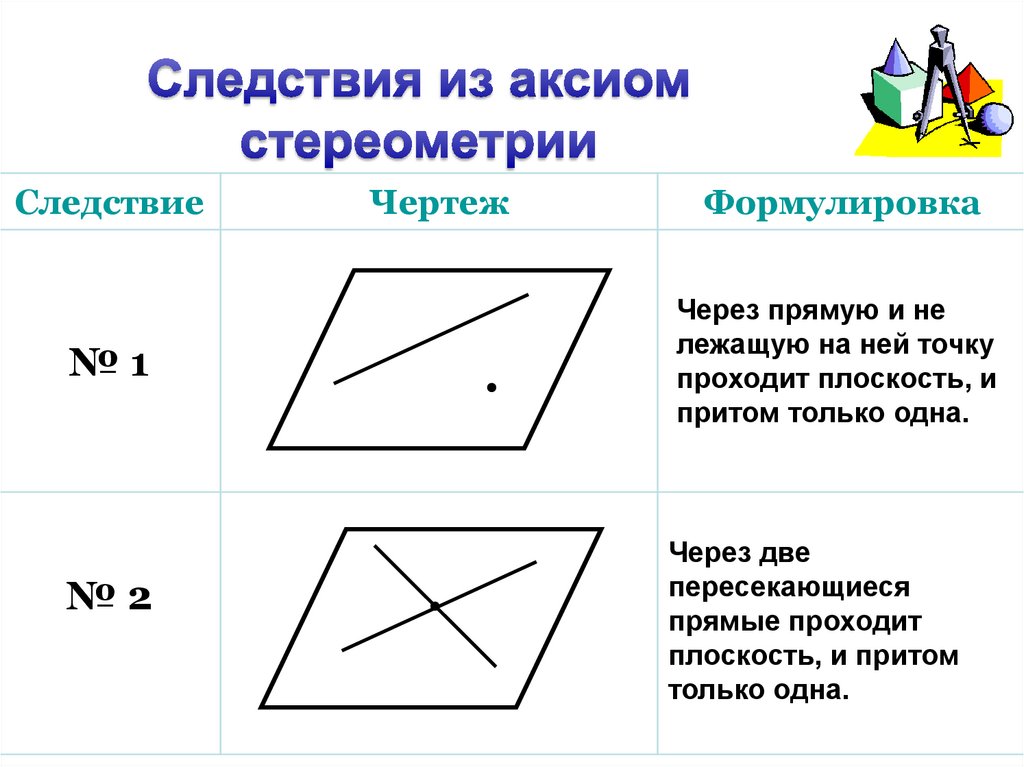
11. Следствия из аксиом стереометрии
Следствие№1
№2
Чертеж
Формулировка
Через прямую и не
лежащую на ней точку
проходит плоскость, и
притом только одна.
Через две
пересекающиеся
прямые проходит
плоскость, и притом
только одна.
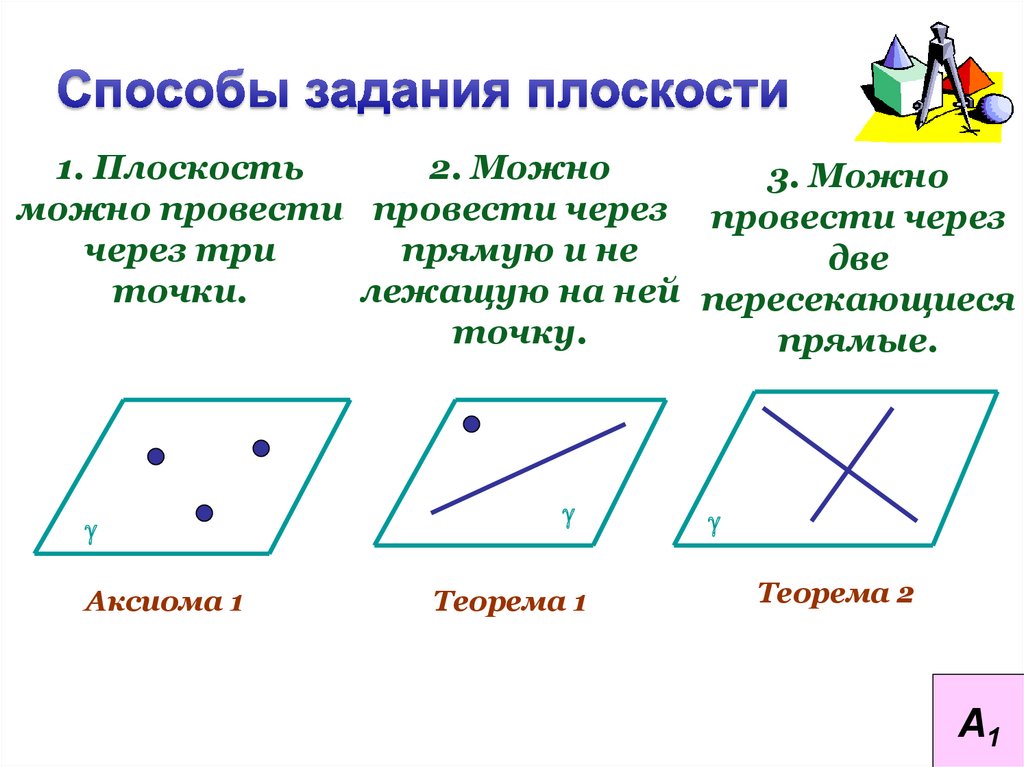
12.
1. Плоскость2. Можно
3. Можно
можно провести провести через провести через
через три
прямую и не
две
точки.
лежащую на ней пересекающиеся
точку.
прямые.
Аксиома 1
Теорема 1
Теорема 2
А1
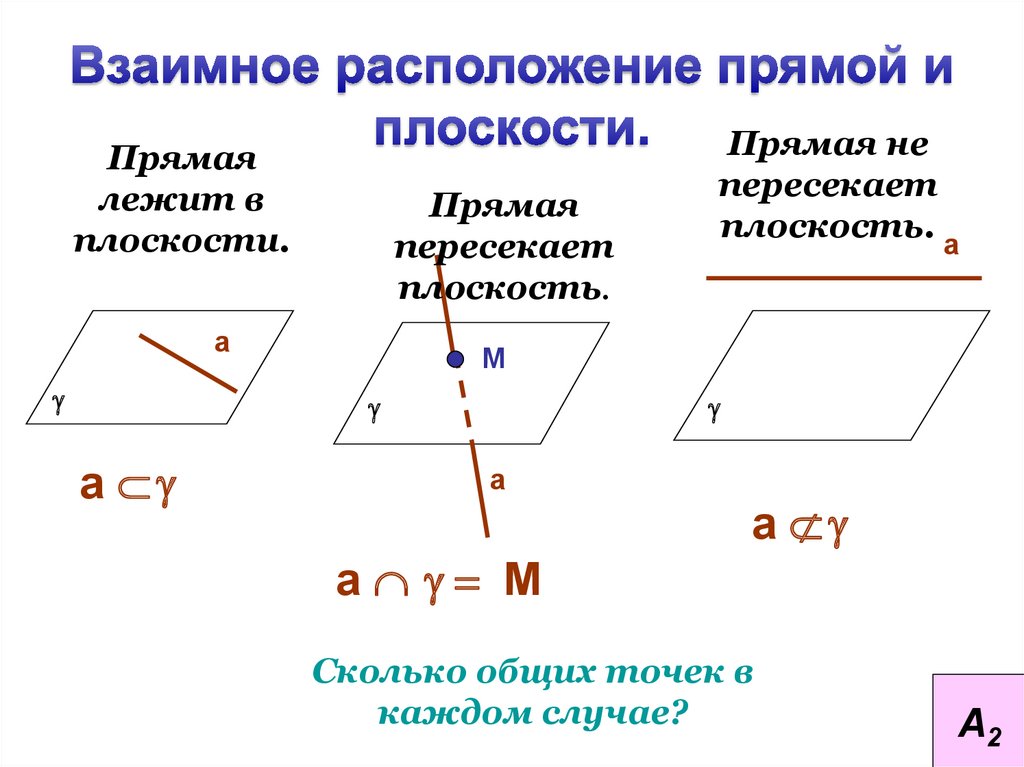
13.
Прямаялежит в
плоскости.
Прямая
пересекает
плоскость.
а
а
М
а
Прямая не
пересекает
плоскость.
а
а
а М
Сколько общих точек в
каждом случае?
А2
14.
Пользуясь даннымрисунком, назовите:
• а) четыре точки,
лежащие в плоскости
SAB, в плоскости АВС;
• б) плоскость, в
которой лежит
прямая MN, прямая
КМ;
• в) прямую, по которой
пересекаются
плоскости ASC и SBC ,
плоскости SAC и CAB.
S
К
C
А
М
N
В
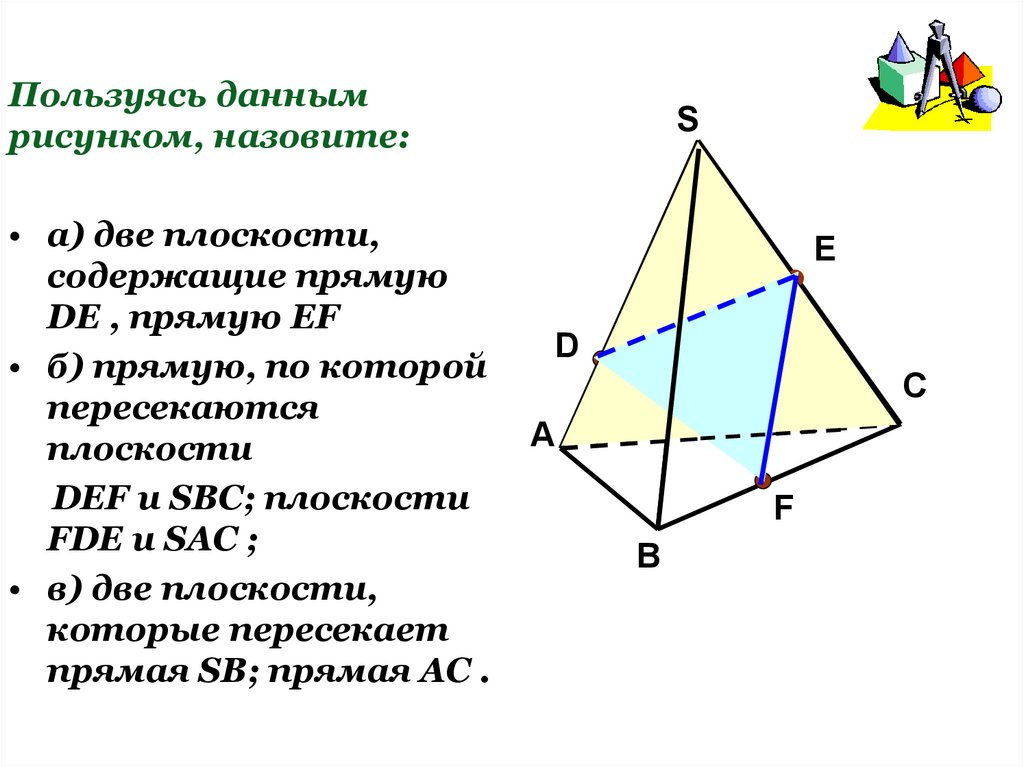
15.
Пользуясь даннымрисунком, назовите:
• а) две плоскости,
содержащие прямую
DE , прямую EF
• б) прямую, по которой
пересекаются
плоскости
DEF и SBC; плоскости
FDE и SAC ;
• в) две плоскости,
которые пересекает
прямая SB; прямая AC .
S
E
D
С
А
F
В
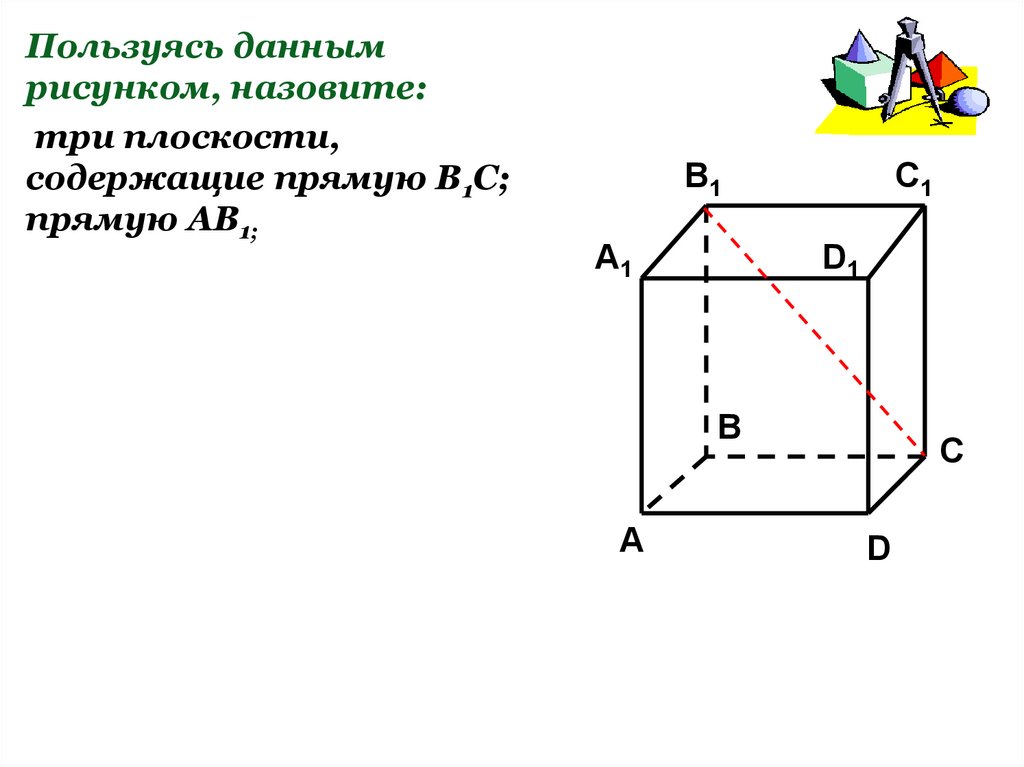
16.
Пользуясь даннымрисунком, назовите:
три плоскости,
содержащие прямую В1С;
прямую АВ1;
B1
A1
C1
D1
B
A
C
D
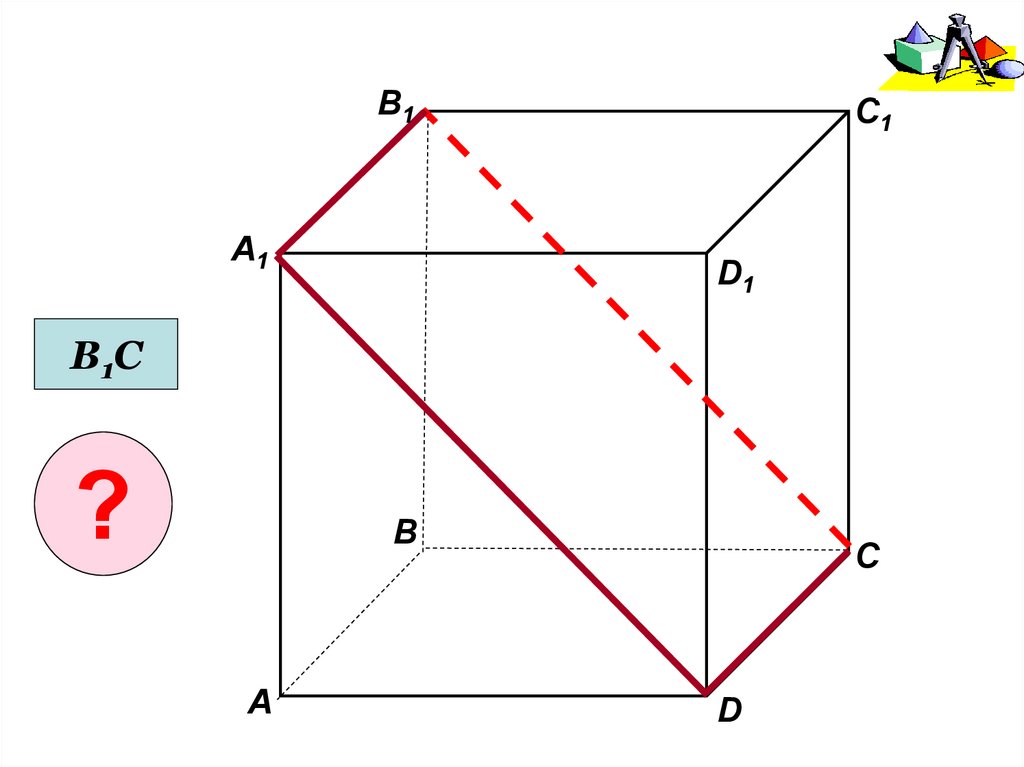
17.
В1А1
C1
D1
В1С
?
В
А
С
D
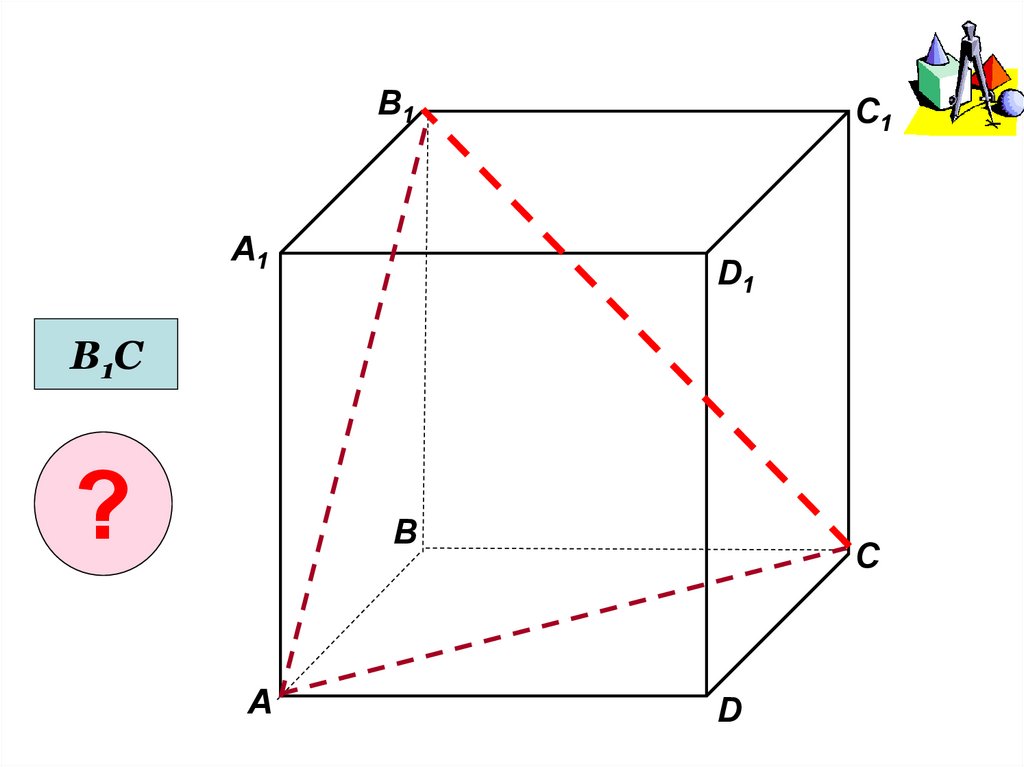
18.
В1А1
C1
D1
В1С
?
В
А
С
D




 Математика
Математика








