Скінченні автомати. (Тема 4)

1. Тема 4. Скінченні автомати

1. Основні означення і поняття
2. Приклад детермінованого скінченного автомату
3. Приклад недетермінованого скінченного
автомату
4. Перетворення недетермінованого скінченного
автомата в детермінований скінченний автомат

2. 1. Основні означення і поняття

3.

Означення 2. Пара {q, ) Q * називається конфігурацією автомата M.
Конфігурація (q 0 , ) називається початковою конфігурацією, а
( q , e) ,
q F - заключною.
Кажуть, що автомат переходить з конфігурації
( q,
a )
a в конфігурацію ( q , ), якщо q (q, a) і позначають це так:
(q, a ) (q , ) .
Робота скінченого автомата – це послідовність конфігурацій. Нехай
K 0 , K 1 ,..., K p - деякі конфігурації автомата. Якщо можна перейти
*
p
K 0 K1 ... K p , то це можна позначити так: K 0 K p або K 0 K p .
Означення 3. Кажуть, що автомат M допускає ланцюжок
, якщо
p
( q0 , ) ( q , e) , де q F .
Означення 4. Мовою, що визначається (допускається) автоматом M,
називається множина вхідних ланцюжків, що допускається цим автоматом.
*
L( M ) { | , ( q0 , ) ( q, e) для деякого q F }
*

4.

5. 2. Приклад детермінованого скінченного автомату

Задача 1. Побудувати автомат в алфавіті ={0,1}, який буде
розпізнавати слова, в яких є два нулі підряд.
1 = 10011 L(M), 2 = 10101101 L(M)
M ({ p, q, r}, {0,1}, , p, {r})
: ( p,0) q, ( p,1) p, (q,0) r , ( q,1) p, (r ,0) r , (r ,1) r.
Cтани
Вхідні символи
0
1
p
{q}
{ p}
q
{r}
{ p}
{r}
{r}
r
( p,01001) (q,1001) ( p,001) (q,01) (r ,1) (r , e).
(01001) L( M ).

6. Wolfram Matematica 10.0 (Дубінін Д.)

7.

Слайд з лекції Ульмана
(Coursera)

8. 3. Приклад недетермінованого скінченного автомату

Задача 2. Побудувати недетермінований скінченний автомат,
який дозволяє такі ланцюжки в алфавіті {1,2,3}, в яких
останній символ ланцюжка зустрічався раніше.
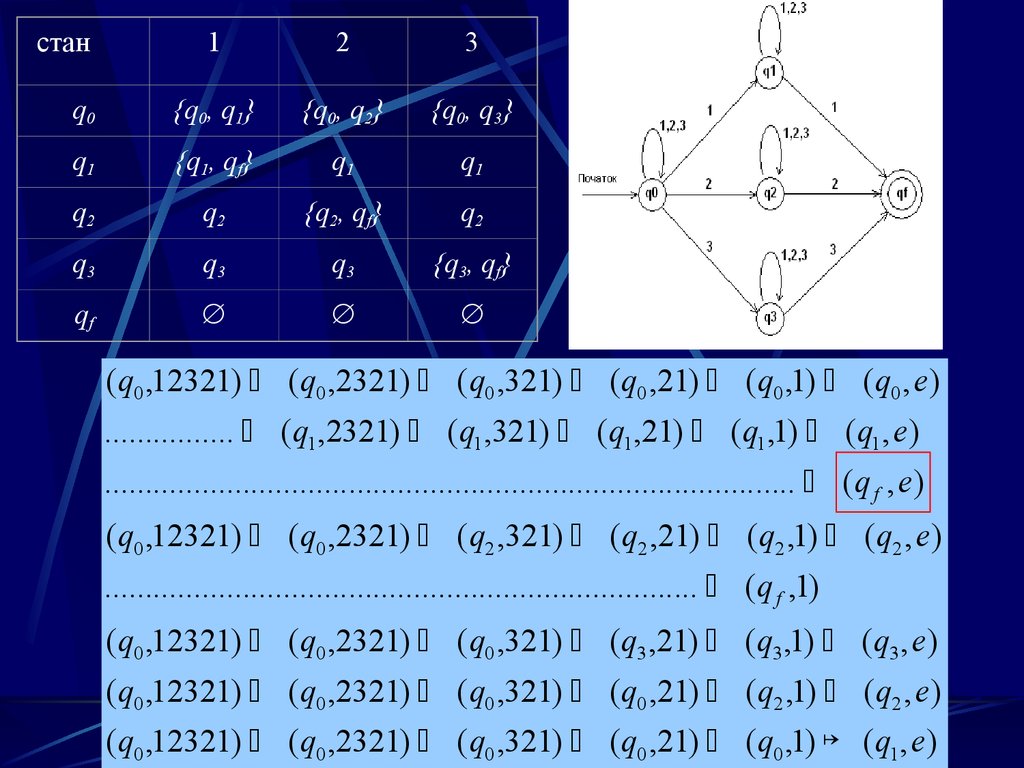
M ({q 0 , q1 , q 2 , q3 , q f }, {1,2,3}, , q 0 , {q f }).
стан
1
2
3
q0
{q0, q1}
{q0, q2}
{q0, q3}
q1
{q1, qf}
q1
q1
q2
q2
{q2, qf}
q2
q3
q3
q3
{q3, qf}
qf

9.

стан
1
2
3
q0
{q0, q1}
{q0, q2}
{q0, q3}
q1
{q1, qf}
q1
q1
q2
q2
{q2, qf}
q2
q3
q3
q3
{q3, qf}
qf
( q0 ,12321) ( q0 ,2321) ( q0 ,321) ( q0 ,21) ( q0 ,1) ( q0 , e)
................ ( q1 ,2321) ( q1 ,321) ( q1 ,21) ( q1 ,1) ( q1 , e)
..................................................................................... ( q f , e)
( q0 ,12321) ( q0 ,2321) ( q2 ,321) ( q2 ,21) ( q2 ,1) ( q2 , e)
......................................................................... ( q f ,1)
( q0 ,12321) ( q0 ,2321) ( q0 ,321) ( q3 ,21) ( q3 ,1) ( q3 , e)
( q0 ,12321) ( q0 ,2321) ( q0 ,321) ( q0 ,21) ( q2 ,1) ( q2 , e)
( q0 ,12321) ( q0 ,2321) ( q0 ,321) ( q0 ,21) ( q0 ,1) ( q1 , e)

10. 4. Перетворення недетермінованого скінченного автомата в детермінований скінченний автомат

Нехай M (Q, , , q 0 , F ) - недетермінований скінченний автомат.
M (Q , , , q0 ' , F ) - детермінований скінченний автомат.
) 1) Побудова множини станів.
Q - множина станів M’, яка будується так: беруться всі можливі
комбінації з множини станів Q . Кожна така комбінація – стан M’.
Наприклад:
нехай q0 , q1 ,..., q8 - стани M (q i Q ). Тоді [ q1 , q3 , q 5 ] - один із станів M’.
Якщо Q має n станів, то Q P (Q ) 2 n станів.
2) Початковий стан: q0 ‘=[q0] .
3) Побудова множини заключних станів.
F складається з усіх таких підмножин S множини P (Q ) , що S F .
Наприклад:
якщо розглянути довільний стан з Q’: [... f i ...] , то [... f i ...] F , якщо
fi F .
4) Побудова функції переходів.
Припустимо, що в нас є деякий стан з множини Q’. Побудувати функцію
переходу ’ для цього стану означає визначити тільки один стан
детермінованого автомату M’.
([ q0 , q1 ,..., qm ], a ) [ r0 , r1 ,..., rk ]
i [0, m ] j [0, k ] : ( qi , a ) rj .

11. Приклад детермінізації автомата

Означення 9. Стан p називається досяжним, якщо існує
ланцюжок такий, що ( q , ) * ( p, e ).
0
Задача 2.
стан
M ({q 0 , q1 , q 2 , q3 , q f }, {1,2,3}, , q 0 , {q f }).
1
2
3
q0
{q0, q1}
{q0, q2}
{q0, q3}
q1
{q1, qf}
q1
q1
q2
q2
{q2, qf}
q2
q3
q3
q3
{q3, qf}
qf
q0 ' [ q0 ] A
( A,1) [ q0 , q1 ] B
( A,2) [q0 , q2 ] C
( A,3) [ q0 , q3 ] D
( B,1) [q0 , q1 , q f ] E
( B,2) [ q0 , q1 , q2 ] F
( B,3) [ q0 , q1 , q3 ] G
(C ,1) [q0 , q1 , q2 ] F
...

12.

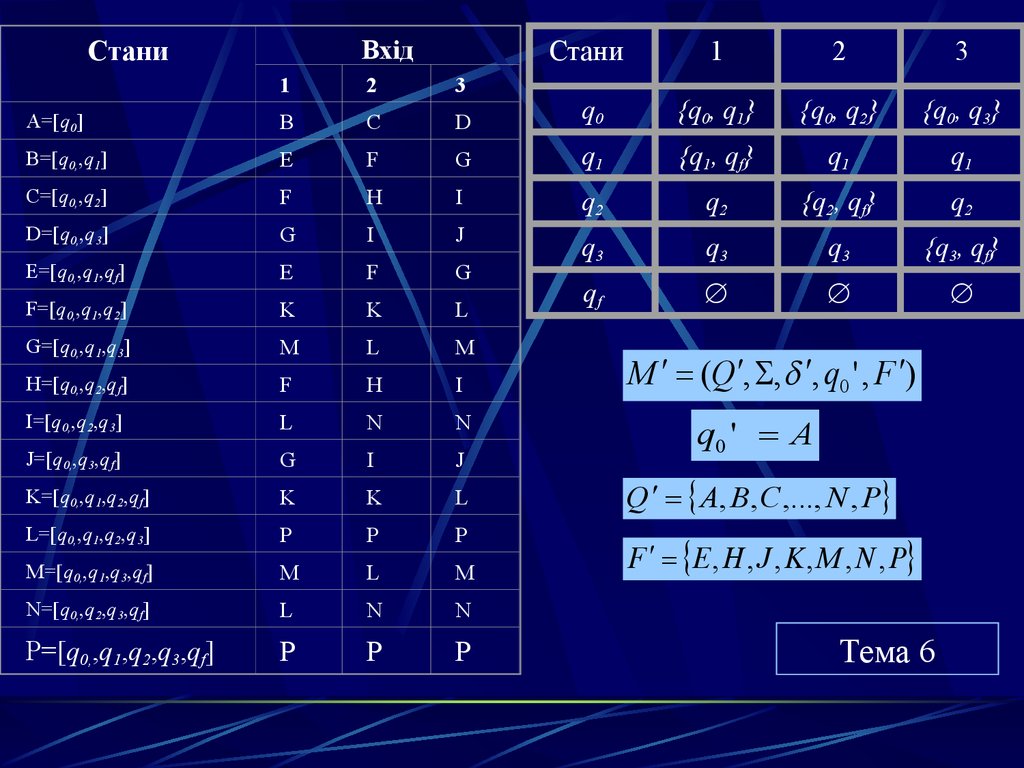
Вхід
Стани
Cтани
1
2
3
1
2
3
A=[q0]
B
C
D
q0
{q0, q1}
{q0, q2}
{q0, q3}
B=[q0,,q1]
E
F
G
q1
{q1, qf}
q1
q1
C=[q0,,q2]
F
H
I
q2
q2
{q2, qf}
q2
D=[q0,,q3]
G
I
J
E=[q0,,q1,qf]
E
F
G
q3
q3
q3
{q3, qf}
F=[q0,,q1,q2]
K
K
L
qf
G=[q0,,q1,q3]
M
L
M
H=[q0,,q2,qf]
F
H
I
I=[q0,,q2,q3]
L
N
N
J=[q0,,q3,qf]
G
I
J
K=[q0,,q1,q2,qf]
K
K
L
L=[q0,,q1,q2,q3]
P
P
P
M=[q0,,q1,q3,qf]
M
L
M
N=[q0,,q2,q3,qf]
L
N
N
P=[q0,,q1,q2,q3,qf]
P
P
P
M (Q , , , q0 ' , F )
q0 ' A
Q A, B, C ,..., N , P
F E , H , J , K , M , N , P
Тема 6