Похожие презентации:
Розв'язання крайових задач (КЗ) для ЗДР
1.
Тема 3. Розв'язання крайовихзадач (КЗ) для ЗДР
1
2.
РОЗВ'ЯЗАННЯ КРАЙОВИХ ЗАДАЧ (КЗ) ДЛЯ ЗДРПостановка лінійної крайової задачі для ЗДР
У
випадку
КЗ
полягає
у
знаходженні
функції
y = y(x) для інтервалу x є [a, b], що задовольняє ДР та крайовим
умовам.
p0 (x) y (n) +p1 (x) y (n-1) +...+ pn (x) y = f (x), x є[a, b], (3.1)
n 1
(k )
(k )
(
y
(
a
)
(b))
к
k y
k 0
Величини
αkν, βkν
і
, ν = 1, 2, …, n
(3.2)
γkν - задані постійні.
p0 (x), p1 (x) ... pn (x), f(x) – задані функції.
В рівняння (3.2) входять n
постійних загального розв'язку.
рівнянь, з яких визначають n
Тема 3 РОЗВ'ЯЗАННЯ КРАЙОВИХ ЗАДАЧ (КЗ) ДЛЯ ЗДР
2
3.
p0 (x) y (n) +p1 (x) y (n-1) +...+ pn (x) y = f (x), x є[a, b],(3.1)
(k )
(k )
(
y
(
a
)
(b))
к
k y
(3.2)
n 1
, ν = 1, 2, …, n
k 0
Введемо на розгляд диференціальний оператор Ly і функционал
lν [y], тоді (2.1) і (2.2) можна записати у вигляді
Ly = f(x),
lν [y] = γν,
або при n = 2
КЗ – однорідна
f (x) = 0
γν= 0
Ly = f(x),
l1 [y] = γ1
l2 [y] = γ2
x є [a,b]
ν = 1, 2,..., n
(3.3)
x є [a,b]
(3.4)
КЗ – напіводнорідна
f(x) = 0
γν ≠ 0
або
f(x) ≠ 0
γν= 0
y(x) Теорема: Для того щоб існувало єдине рішення неоднорідної
КЗ, необхідно і достатньо, щоб однорідна КЗ мала тільки
тривіальний розв'язок ≡ 0
Тема 3 РОЗВ'ЯЗАННЯ КРАЙОВИХ ЗАДАЧ (КЗ) ДЛЯ ЗДР 3
4.
МЕТОД СКІНЧЕННИХ РІЗНИЦЬДля ЗДР 2-го порядку
y II + p(x) yI + q(x) y = f(x),
x є[a, b],
0 y(a) 1 y (a)
0 y(b) 1 y (b)
(3.5)
(3.6)
Розіб'ємо проміжок [a, b] на n рівних частин довжиною
h = (b – a) / n.
Координати вузлів : xi = a + i·h, i = 0, 1, ...n.
x0 і x n – крайові (граничні),
x1, x2, …, xi , …, x n-1 – центральні (внутрішні).
y
y = y(x)
y0
a
y1
y2
y3
yi
x0
x1
x2
x3
xi
h
h
h
h
h
yn
Обозначим
y (xi ) = yi ,
p (xi ) = pi ,
f (xi ) = fi.
X
b
xn
4
5.
Апроксимуємопохідні
скінченно
різницевими
відношеннями, які дозволяють замінити диференціальні
рівняння системою лінійних алгебраїчних рівнянь (СЛАР), щодо
невідомих значень функції yi в точках xi (i = 0, 1... n)
У внутрішніх вузлах xi
замінимо похідні формулами
центральних різниць
yi tg
yi 1 yi 1
2h
(3.7)
yi 1 yi
yi 1 2 yi yi 1
yi ( yi ) (
)
h
h2
(3.8)
Для граничних вузлів використовуємо праві (ліві) різниці
y1 y0
y0
,
h
yn yn 1
yn
h
(3.9)
5
6.
yi II + p(xi) yiI + q(xi) yi = f(xi),0 y( x0 ) 1 y ( x0 )
0 y ( xn ) 1 y ( xn )
i = 1, ..., n -1 ,
(3.5)
y1 y0 yn yn 1 (3.6)
y0 yn ,
h
h
В ДР (3.5) похідні замінюються центральними різницями
для кожного внутрішнього вузла (3.8), а в рівняннях (3.6) різницями для крайових вузлів (3.9).
Внаслідок цього система диф. рівнянь перетворюється на
СЛАР
yi 1 2 yi yi 1
yi 1 yi 1
pi
qi yi f i
2
h y y
2h
0 y 0 1 1 0
yn hyn 1
0 yn 1
h
i = 1, ..., n-1
(3.10)
(3.11)
6
7.
yi 1 2 yi yi 1yi 1 yi 1
pi
qi yi f i
2
h
2h
y1 y0
0 y 0 1
h
yn yn 1
0 yn 1
h
Після перетворень отримаєм
( 0h 1 ) y0 1 y1 h
h
h
2
(1 pi ) y i 1 (h qi 2) y i (1 pi ) y i 1 f i h 2
2
2
(3.10)
(3.11)
(3.12)
, i = 1, 2,...n-1
1 yn 1 ( 0h 1 ) yn h
Отримана система (3.12) є СЛАР з трьохдіагональною
матрицею коефіцієнтів.
Розв'язується методом прогону.
7
8.
Метод скінченних різниць для вирішення крайовоїзадачі для ЗДР 2-го порядку.
Приклад 1
Знайти вирішення крайової задачі із заданими крайовими умовами
методом скінченних різниць на відрізку[a; b] з кроком h
y p( x) y q ( x) y f ( x)
А0 y (a) А1 y I (a ) А
В0 y (b) В1 y I (b) В
y 3 y 1 / xy 1 x - ЗДР 2-го порядку
9 y (1,6) 10 y (1,6) 4,5
7 y (1,9) 8 y (1,9) 3,5
- крайові умови
На відрізку x 1,6;1,9 будуємо сітку з кроком h = 0,1.
х0 = 1,6, – граничний вузол
Отримаємо чотири вузли
х1 = 1,7,
– внутрішні вузли
сітки з абсцисами
х2 = 1,8,
х3 = 1,9. – граничний вузол
Система ДР набуде вигляду
А0 y0 А1 y0 А
y kII pk y k qk y k f k , k = 1, 2
В0 y3 В1 y3I В
8
9.
А0 y0 А1 y0 АРівняння у внутрішніх вузлах
y kII pk y k qk y k f k , k = 1, 2 х і х замінимо скінченно 1
2
різницевими рівняннями :
В0 y3 В1 y3I В
y k 1 y k 1 центральні різниці для
yk 1 2 yk yk 1
yk
y k
внутрішніх вузлів
2
h
2h
y k 1 2 y k y k 1
y k 1 y k 1
pk
qk y k f k , k = 1, 2
2
2h
h
або
y k 1 2 y k y k 1
y k 1 y k 1 1
3
y k 1 xk , k = 1, 2
2
2h
xk
h
Після перетворень отримаємо
3h
3h
2 1
(1 ) yk 1 (h
2) yk (1 ) yk 1 h 2 (1 xk ) , k = 1, 2
2
xk
2
9
10.
А0 y0 А1 y0 Аy kII pk y k qk y k f k , k = 1, 2
В0 y3 В1 y3I В
y1 y0
y0
h
y3 y 2
y3
h
Ліві (праві) різниці
граничних вузлів х0 і х3
для
-9,1 y0 + 10 y1 = 0,45
-8 y2 + 8,7 y3 = 0,35
приєднаємо до отриманої
системи рівнянь
Таким чином, задача зводиться до розв'язання СЛАР
( А0 h А1 ) y0 А1 y1 Аh
hp
hp
(1 1 ) y0 (h 2 q1 2) y1 (1 1 ) y2 h 2 f1
2
2
hp2
hp2
2
(1
) y1 (h q2 2) y2 (1
) y3 h 2 f 2
2
2
В1 y2 ( В0 h В1 ) y3 Вh
10
11.
Для даної задачі система має вигляд-9,1 y0 + 10 y1 = 0,45
3h
3h
2 1
(1 ) y0 (h
2) y1 (1 ) y2 h 2 (1 x1 )
2
x1
2
3h
1
3h
(1 ) y1 (h 2 2) y2 (1 ) y3 h 2 (1 x2 )
2
x2
2
-8 y2 + 8,7 y3 = 0,35
після обчислення коефіцієнтів
система рівнянь виглядає так:
9,1 y0 + 10 y1 = 0,45
0,85 y0 - 2,0059 y1 + 1,15 y2 = 0,027
0,85 y1 - 2,0056 y2 + 1,15 y3 = 0,028
-8 y2 + 8,7 y3 = 0,35
В результаті розв'язання системи рівнянь
(методом прогону або за допомогою оберненої
матриці) отримаємо значення невідомих системи
рівнянь
xk
1,6
1,7
1,8
1,9
yk
-1,312
-1,149
-1,011
-0,890
11
12.
Метод скінченних різниць для вирішення крайовоїзадачі для ЗДР 2-го порядку.
Приклад 2
На інтервалі [0; 0,5] знайти рішення крайової задачі для ЗДР 2-го
порядку методом скінченних різниць при h=0,1
y
2 0,1N
6 N
y
y 0
2
2
x 1
1 x
y ( 0) 1
y (0,5) 6
На відрізку
- крайові умови
x 0;0,5
будуємо сітку з кроком h = 0,1.
Отримаємо шість вузлів
сітки з абсцисами
Система
ДР
набуде вигляду
- ЗДР 2-го порядку
y0 1
х0 = 0
х1 = 0,1,
х2 = 0,2,
х3 = 0,3,
х4 = 0,4,
х5 = 0,5
ykII pk yk qk yk 0
y5 6
– граничний вузол
– внутрішні вузли
– граничний вузол
, k = 1, 2, 3, 4
12
13.
y0 1Система
ДР
набуде вигляду
де
ykII pk yk qk yk f k
y5 6
2 0,1N
рk
2
xk 1
qk
6 N
1 xk
2
, k = 1, 2, 3, 4
fk 0
Після перетворень отримаємо систему лінійних алгебраїчних
рівнянь (СЛАР)
pk h
pk h
2
(1
) yk 1 (h qk 2) yk (1
) yk 1 h 2 f k
2
2
, k = 1, 2, 3, 4
Таким чином, задача зводиться до вирішення СЛАР, що
складається з 4-х рівнянь з 6 невідомими у0 , у1 , у2 , у3 , у4 , у5
13
14.
hp1hp1
2
(1
) y 0 (h q1 2) y1 (1
) y 2 h 2 f1
2
2
hp
hp
(1 2 ) y1 (h 2 q2 2) y 2 (1 2 ) y3 h 2 f 2
2
2
hp3
hp3
2
(1
) y 2 (h q3 2) y3 (1
) y4 h 2 f 3
2
2
hp
hp
(1 4 ) y3 (h 2 q4 2) y 4 (1 4 ) y5 h 2 f 4
2
2
«Зайві» невідомі виключаються за допомогою крайових
умов : y(0) = y0 = 1 и y(0,5)= y5 = 6
hp1
hp
) y2 h 2 f1 (1 1 ) y0
2
2
hp
hp
(1 2 ) y1 (h 2 q2 2) y 2 (1 2 ) y3 h 2 f 2
2
2
hp3
hp
2
(1
) y 2 (h q3 2) y3 (1 3 ) y 4 h 2 f 3
2
2
hp4
hp
(1
) y3 (h 2 q4 2) y4 h 2 f 4 (1 4 ) y5
2
2
(h 2 q1 2) y1 (1
14
15.
Враховуючи що f(x) = 0hp1
hp
) y2 (1 1 ) y0
2
2
hp
hp
(1 2 ) y1 (h 2 q2 2) y2 (1 2 ) y3 0
2
2
hp3
hp
2
(1
) y2 (h q3 2) y3 (1 3 ) y4 0
2
2
hp4
hp
2
(1
) y3 (h q4 2) y4 (1 4 ) y5
2
2
або
hp
hp
(h 2 q1 2) y1 (1 1 ) y2 (1 1 ) ( 1)
2
2
(h 2 q1 2) y1 (1
(1
hp2
hp
) y1 (h 2 q2 2) y 2 (1 2 ) y3 0
2
2
(1
hp3
hp
) y 2 (h 2 q3 2) y3 (1 3 ) y 4 0
2
2
hp
hp
(1 4 ) y3 (h 2 q4 2) y3 (1 4 ) ( 6)
2
2
Після обчислення
коефіцієнтів система
рівнянь виглядає так :
b1 y1 a1 y2 d1
b2 y1 a2 y2 c2 y3 d 2
b3 y2 a3 y3 c3 y4 d 3
b4 y3 a4 y4 d 4
15
16.
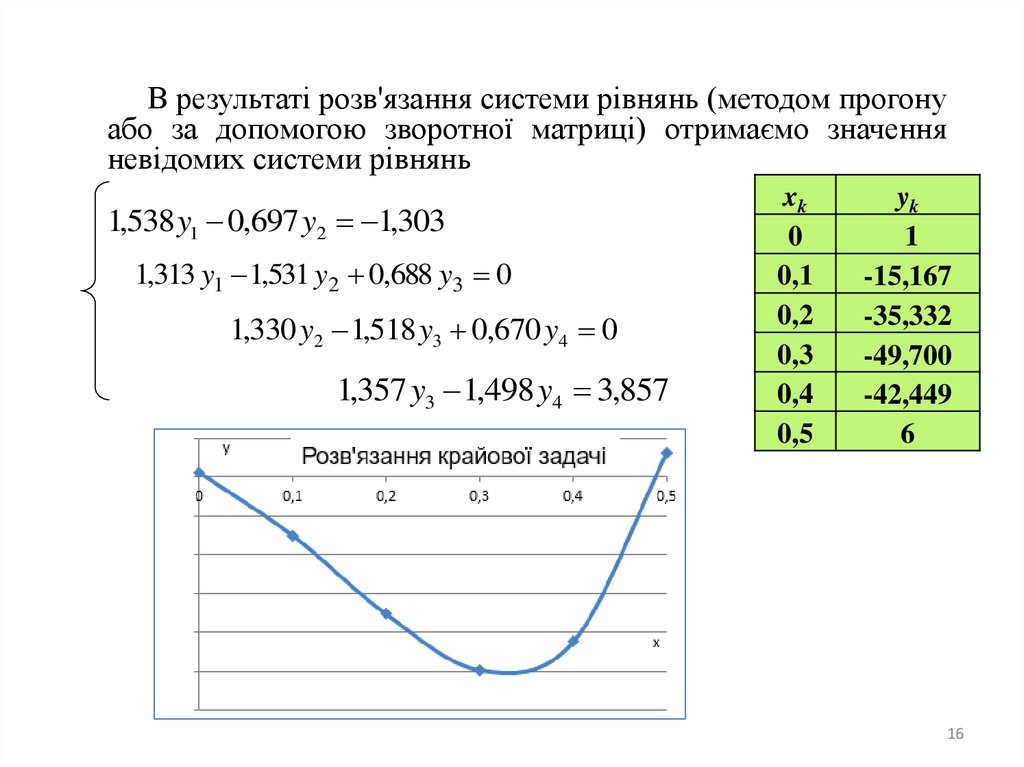
В результаті розв'язання системи рівнянь (методом прогонуабо за допомогою зворотної матриці) отримаємо значення
невідомих системи рівнянь
1,538 y1 0,697 y2 1,303
1,313 y1 1,531 y2 0,688 y3 0
1,330 y2 1,518 y3 0,670 y4 0
1,357 y3 1,498 y4 3,857
xk
0
0,1
0,2
0,3
0,4
0,5
yk
1
-15,167
-35,332
-49,700
-42,449
6
16
17.
Контрольна роботаЗавдання 2. Задача 2 Розв'язання крайової задачі для
ЗДР 2-го порядку методом скінченних різниць
На інтервалі [0; 0,5] знайти розв'язання крайової задачі
для диференціального рівняння
y
2 0,1N
6 N
y
y 0
2
2
x 1
1 x
з крайовими умовами y(0) = 1 і y(0,5) = 6 методом
скінченних різниць при h=0,1.
N - номер варіанта.
17
















 Математика
Математика








