Похожие презентации:
Параллельные прямые
1.
Тема урока:«Параллельные
прямые»
УРОК-ОБОБЩЕНИЯ
Учитель математики Яковлева Н.Н.
ГБОУ ООШ с.Краснояриха
2.
Параллельные сутьпрямые, которые,
находясь в одной
плоскости и будучи
продолжены в обе
стороны
неограниченно, ни с
той, ни с другой
«стороны» между
собой не
встречаются.
Евклид
3.
План урока:Устная работа
Решение задач
Тест
Подведение итогов
Домашнее задание
4.
Устный опрос1.
2.
3.
4.
Дайте определение параллельных прямых.
Что такое секущая? Назовите пары углов,
которые образуются при пересечении двух
прямых секущей.
Сформулируйте признаки параллельности
двух прямых.
Какие утверждения называются аксиомами?
5.
5. Сформулируйте аксиому параллельных прямых.6. Какое утверждение называется следствием?
7. Сформулируйте следствия из аксиомы
параллельных прямых.
8. Какая теорема называется обратной?
9. Сформулируйте свойства параллельных прямых.
6.
Решите письменно:n
7
5
3
1
p
8
6
4
2
m
Назовите пары
накрест лежащих,
соответственных и
односторонних углов.
7.
CD
O
A
B
AO=DO,
CO=BO
Доказать:
AB ║ CD
8.
а7
8
5
6
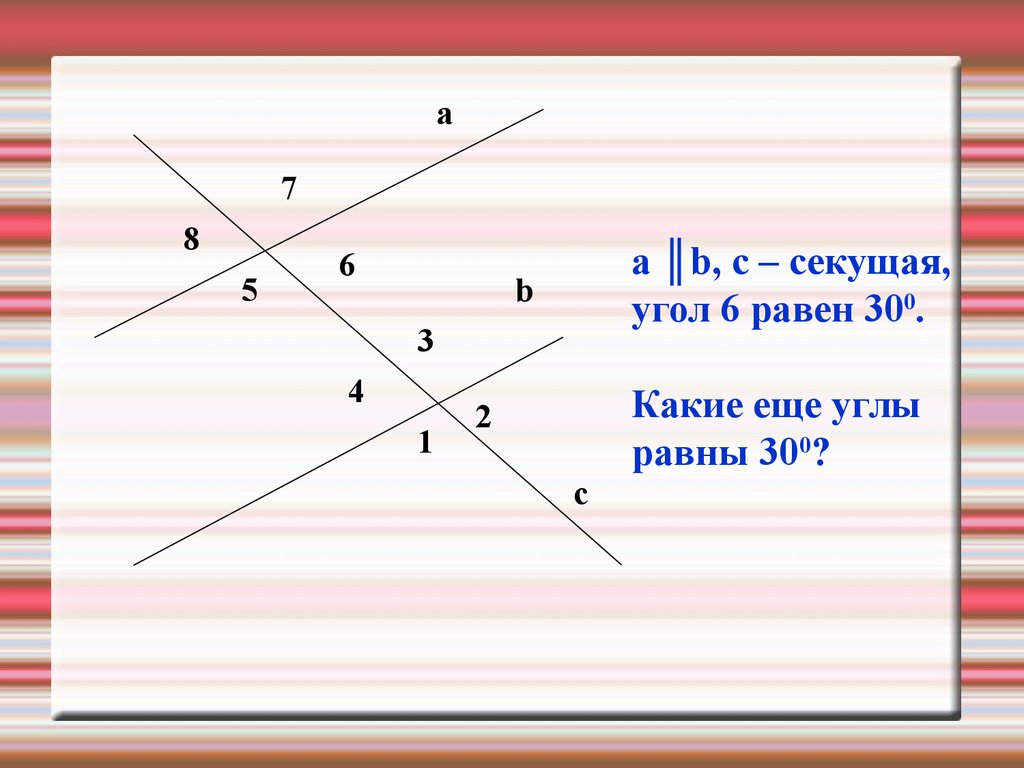
a ║b, c – секущая,
угол 6 равен 300.
b
3
4
1
2
c
Какие еще углы
равны 300?
9.
mn
8
5
3
7
6
4
2
1
p
m ║ n, p –
секущая, угол 1
равен 1250.
Найдите
величины
остальных углов.
10.
аb
100
c
100
d
a ║ b.
Параллельны ли а и
с?
11.
cа
2
b
1
a ║ b. 1=2 2
Найти :
1 , 2.
12.
Решите письменно:а
130
20
1
b
20
c
3
2
d
d
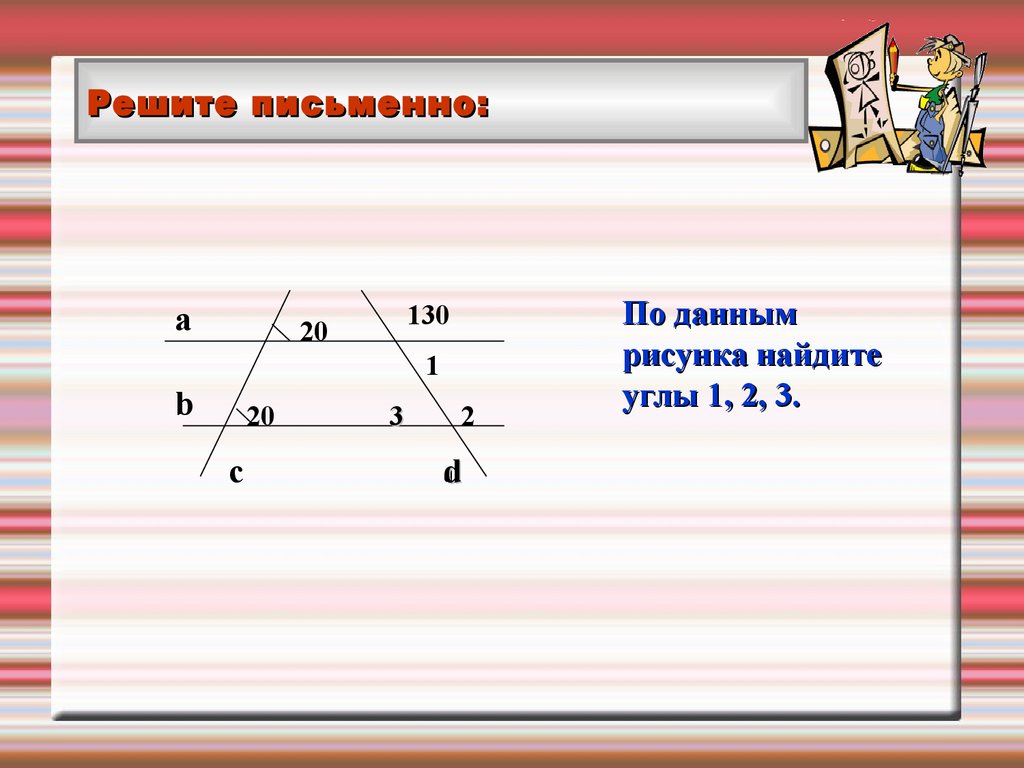
По данным
рисунка найдите
углы 1, 2, 3.
13.
Решите письменно:A
N
C
K
E
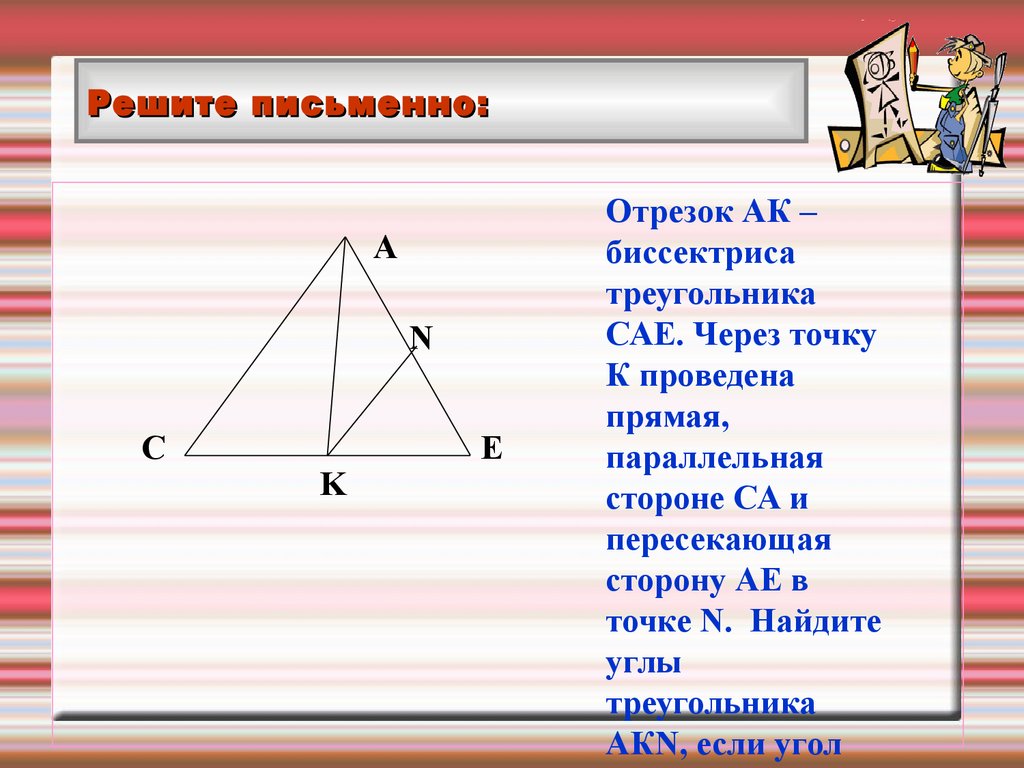
Отрезок АК –
биссектриса
треугольника
САЕ. Через точку
К проведена
прямая,
параллельная
стороне СА и
пересекающая
сторону АЕ в
точке N. Найдите
углы
треугольника
АКN, если угол
14.
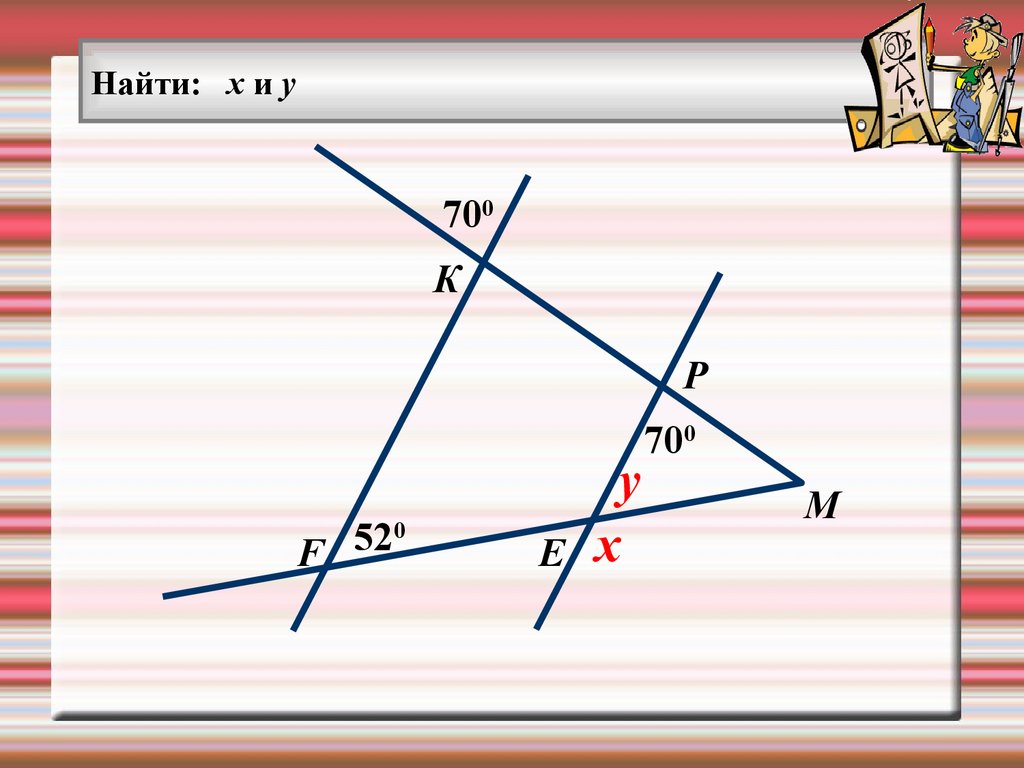
Найти: х и у700
К
Р
F 52
0
Е
y
x
700
М
15.
Найти:BDE
В
D
E
370
А
С
16.
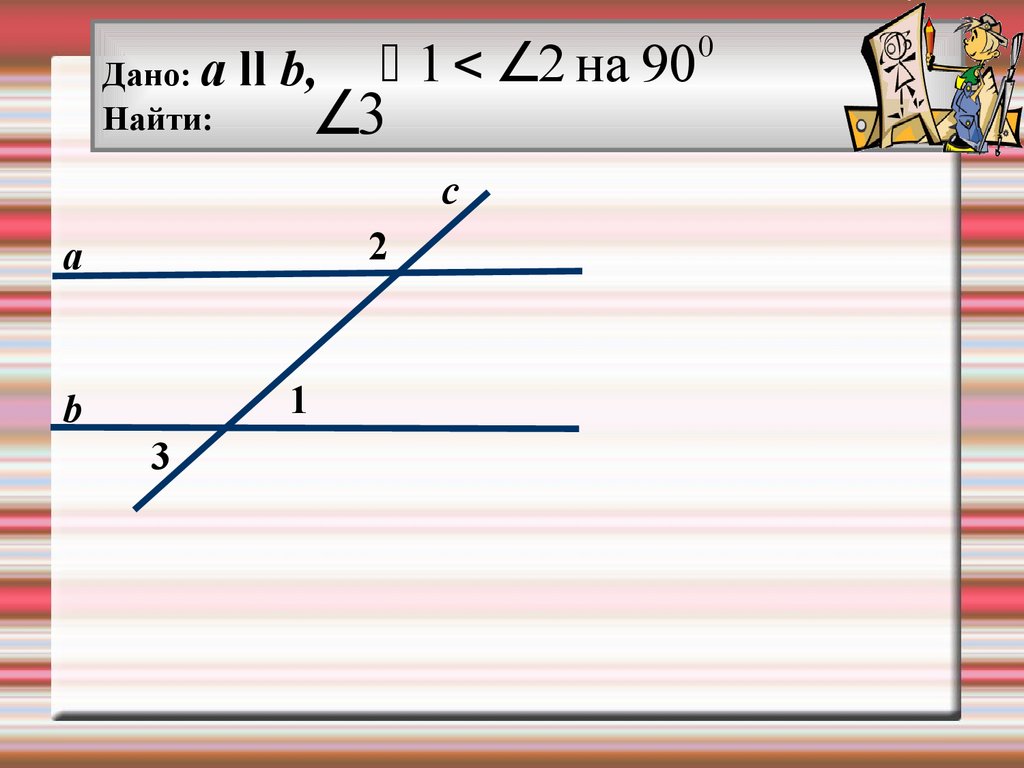
Дано: аНайти:
ll b,
1 2 на 90
3
с
2
а
1
b
3
0
17.
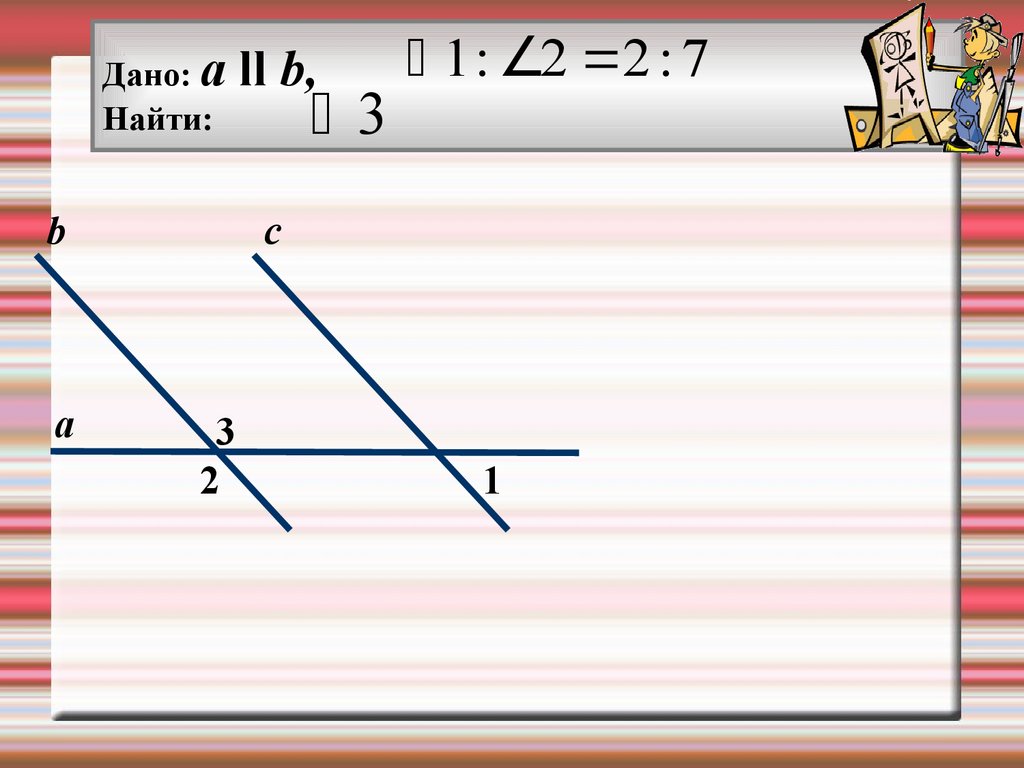
Дано: аНайти:
b
а
ll b,
3
1 : 2 2 : 7
с
3
2
1
18.
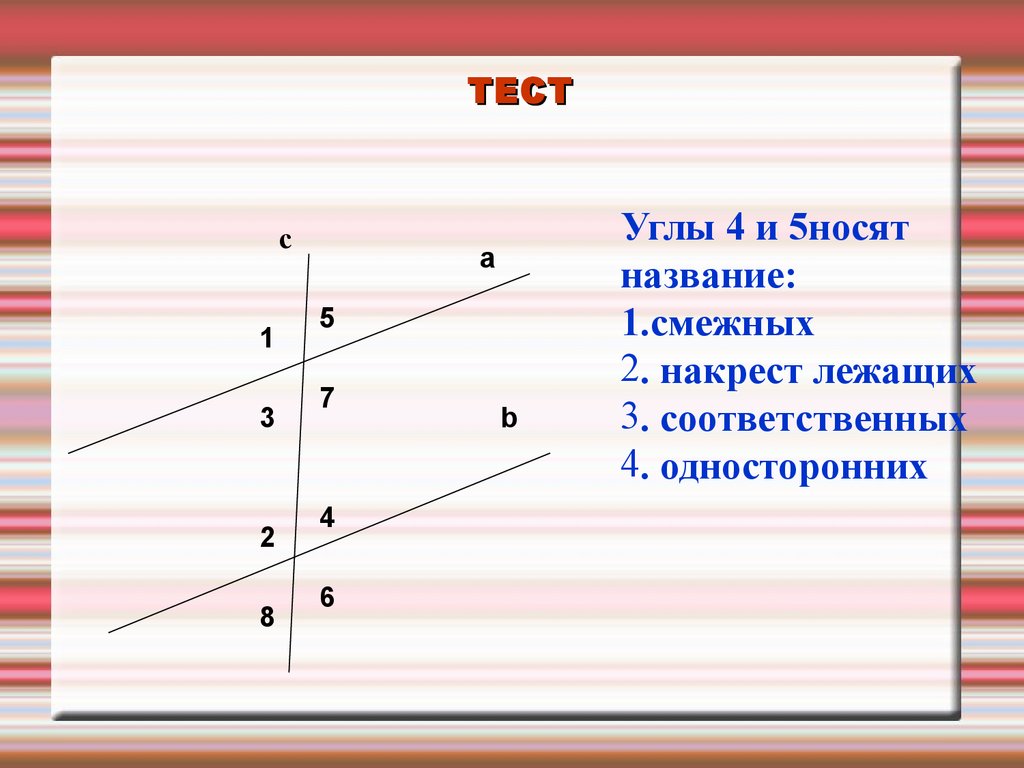
ТЕСТс
1
3
2
8
a
5
7
4
6
b
Углы 4 и 5носят
название:
1.смежных
2. накрест лежащих
3. соответственных
4. односторонних
19.
5Прямые a и b
параллельны если:
1. 2 = 5
7
2.
1=
3
3.
2=
7
4.
5+
4 =1800
с
1
3
2
8
a
4
6
b
20.
Две прямые на плоскости называютсяпараллельными, если:
1. они имеют одну общую точку;
2. не имеют общих точек.
21.
Две прямые на плоскости могут иметь:1. две общие точки;
2. три общие точки;
3. одну общую точку;
4. бесчисленное множество точек.
22.
a ║ b и c┴
a , то
1) с ║ b,
2) c
┴
b.
23.
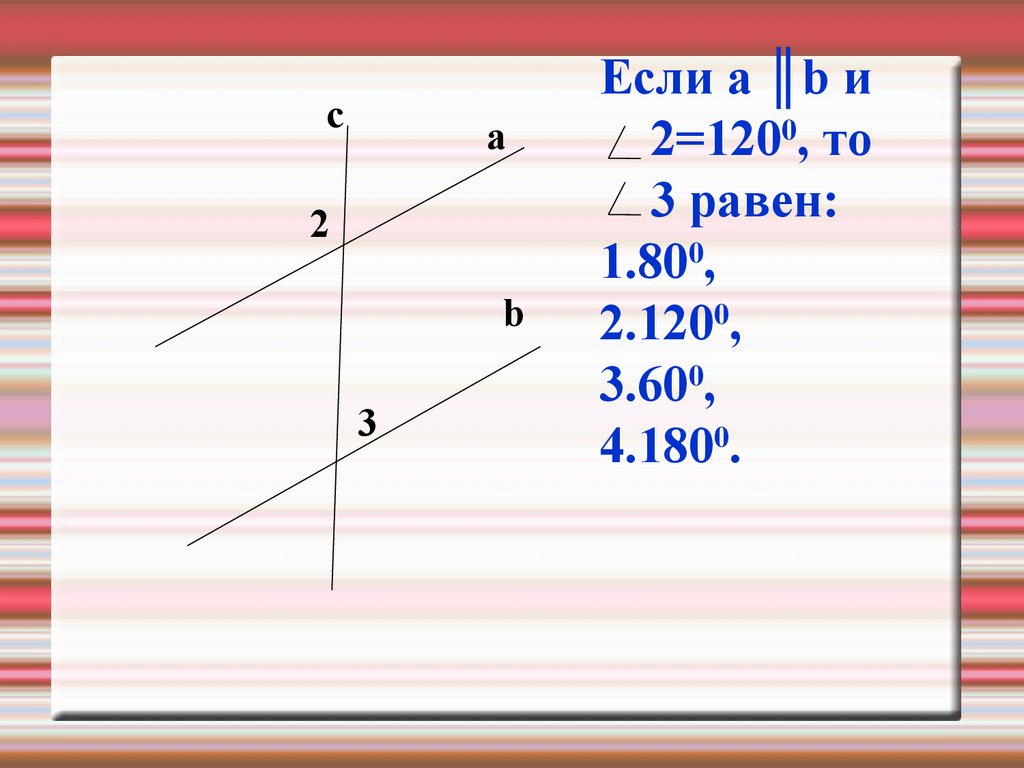
сa
2
b
3
Если а ║b и
2=1200, то
3 равен:
1.800,
2.1200,
3.600,
4.1800.
24.
3c
1
d
2
4
a
b
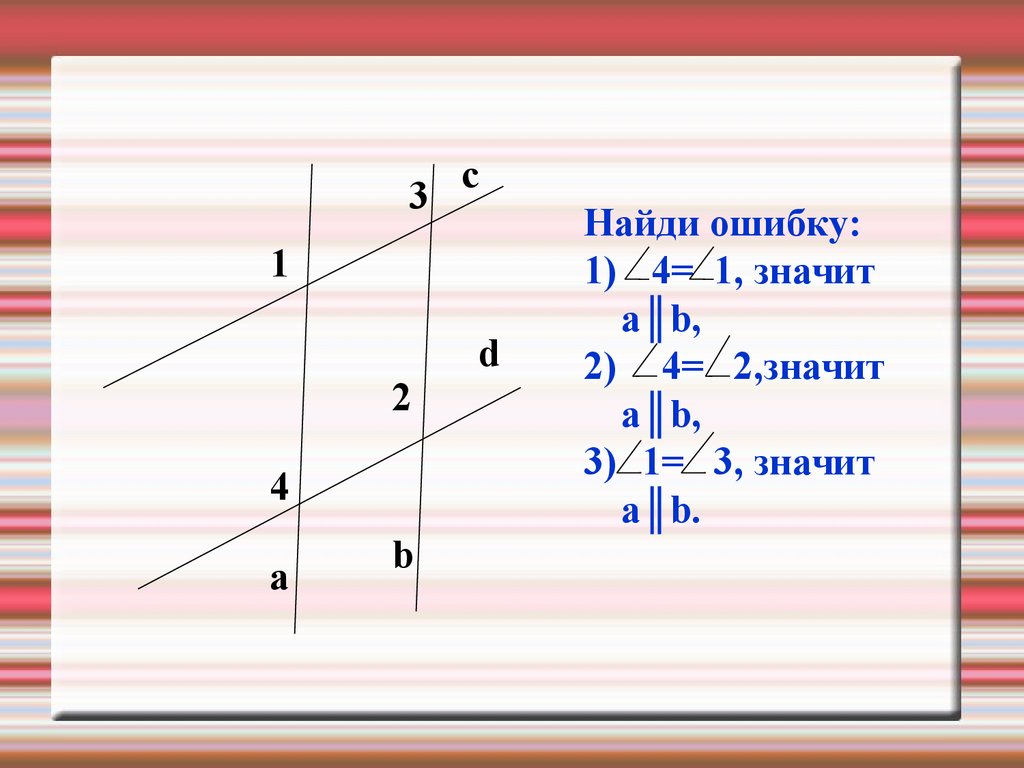
Найди ошибку:
1) 4= 1, значит
а║b,
2) 4= 2,значит
a║b,
3) 1= 3, значит
a║b.
25.
Через точку М, не лежащую на прямой а можнопровести:
1. две прямые, параллельные а;
2. бесчисленное множество прямых, параллельных а;
3. одну прямую, параллельную а.
26.
Если а ║b, b ║c, то:1. а пересекает прямую с,
2. а перпендикулярна с (а с),
┴
3. а ║с.
27.
Правильные ответы:1.
2.
3.
4.
5.
6.
7.
3
3
2
3
2
3
1
8. 3
9. 3
28.
ОЦЕНКА«5» - 9 правильных ответов
«4» - 7 - 8
«3» - 5 - 6
«2» - менее 5
29.
Задание на дом:Вопросы для повторения к главе 3.
№№ 213, 215, 216.
30.
Спасибо заурок!





















 Математика
Математика