Геометрия «на клетчатой бумаге»

1. Геометрия «на клетчатой бумаге»

Подготовка к ГИА и ЕГЭ
Часть 1
Геометрия
«на клетчатой бумаге»
Подготовила учитель математики
Иванова О.В

2. теорема Пифагора, соотношения между сторонами и углами в прямоугольном треугольнике, свойства всех плоских фигур, изучаемых в

• При решении задач с использованием
клетчатой бумаги важно помнить, что
«клеточки» должны помогать! А значит,
нужно подумать как они могут помочь. По
«клеточкам» легко построить
прямоугольный треугольник.
Следовательно, могут помочь все
теоретические факты связанные с
прямоугольным треугольником.
• Решение таких задач не предполагает
использование циркуля и линейки, а
осуществляется непосредственно на
рисунке клетчатой бумаги.
теорема Пифагора,
соотношения между сторонами и углами в
прямоугольном треугольнике,
свойства
всех плоских фигур, изучаемых в школе.

3.

Вычислите длину отрезка АВ, изображённого на
рисунке

4.

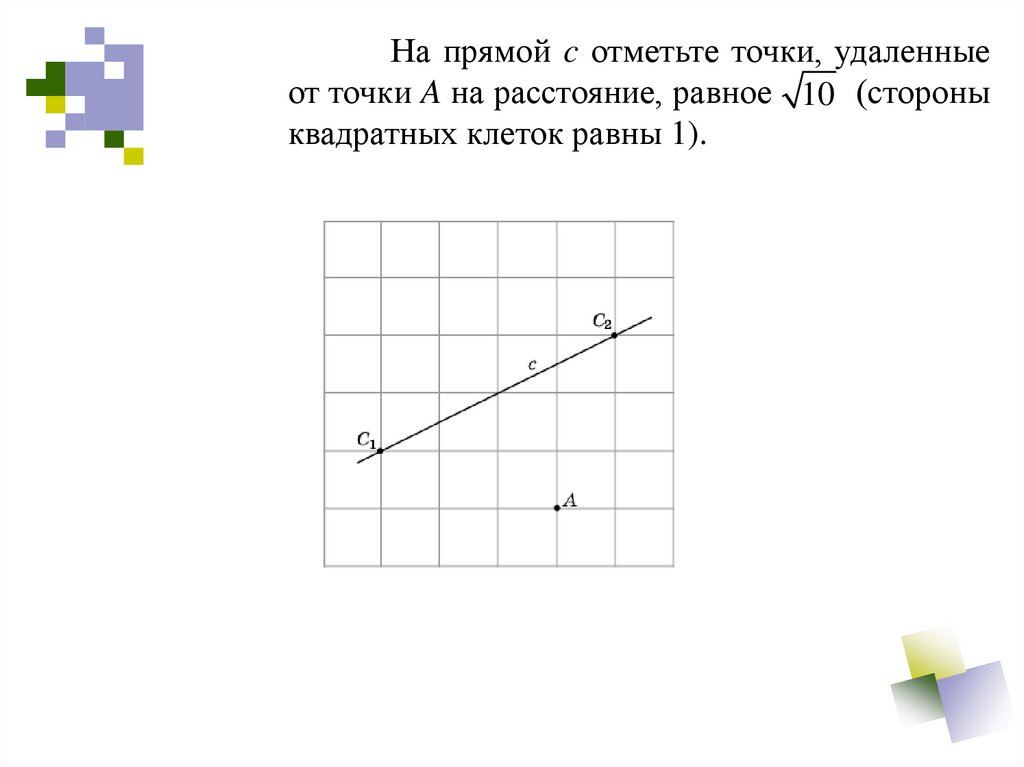
На прямой c отметьте точки, удаленные
от точки A на расстояние, равное 10 (стороны
квадратных клеток равны 1).

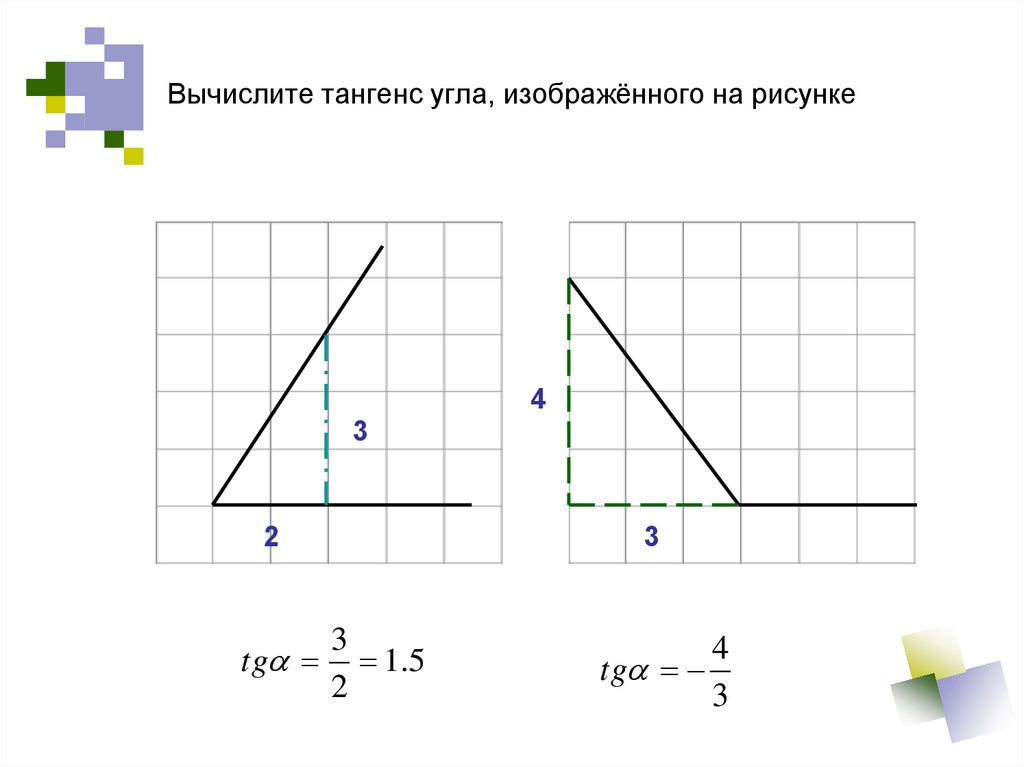
5. Вычислите тангенс угла, изображённого на рисунке

4
3
2
tg
3
3
1.5
2
4
tg
3

6.

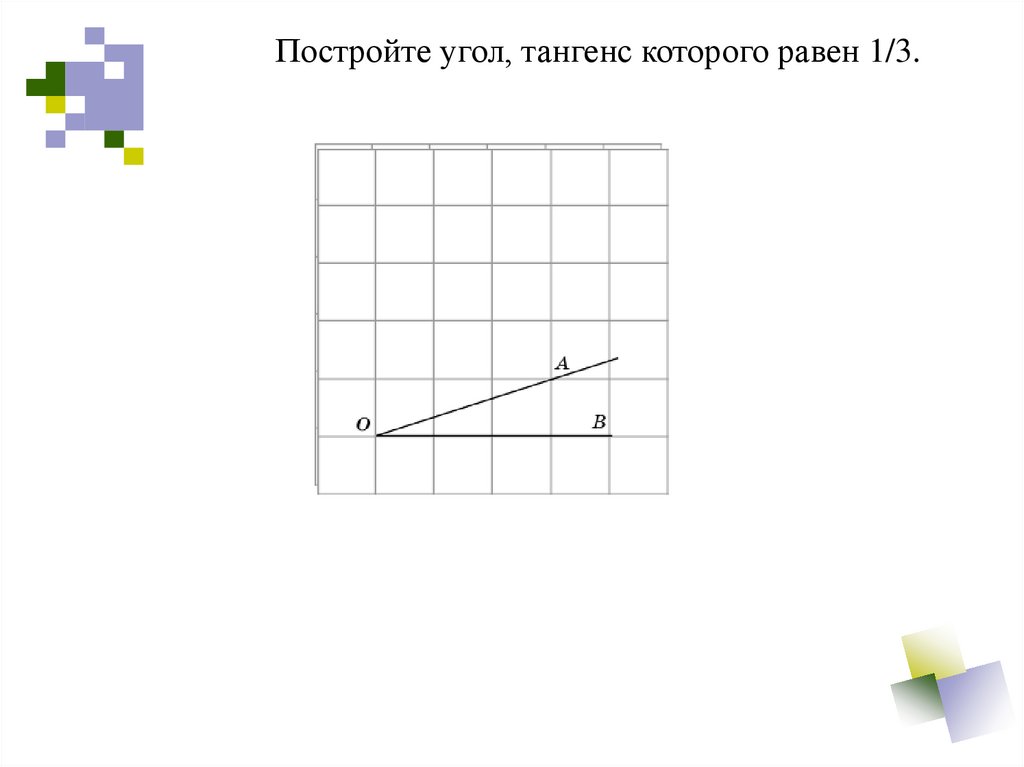
Постройте угол, тангенс которого равен 1/3.

7.

Через точку A проведите
образующую с прямой AB угол 45о.
прямую
AC,

8.

ВЫВОД:
необходимо запомнить,
треугольник
АСМ
–
прямоугольный
равнобедренный.
5
10
М
5
что
и

9.

Докажите, что прямые AB и CD
параллельны.
1 способ
CDO BAO
(по 3 сторонам)
D A
Значит, AB ll CD.
О

10.

Докажите, что прямые AB и CD
параллельны.
2 способ
прямые AB и CD параллельны,
если их угловые коэффициенты
равны.
к CD
2
3
к AB
Значит, AB ll CD.
2
3

11.

Постройте через точку C прямую CD,
параллельную AB.
ВЫВОД: необходимо запомнить, что прямые
параллельны, если их угловые коэффициенты равны.
к AB
у
tg
х

12.

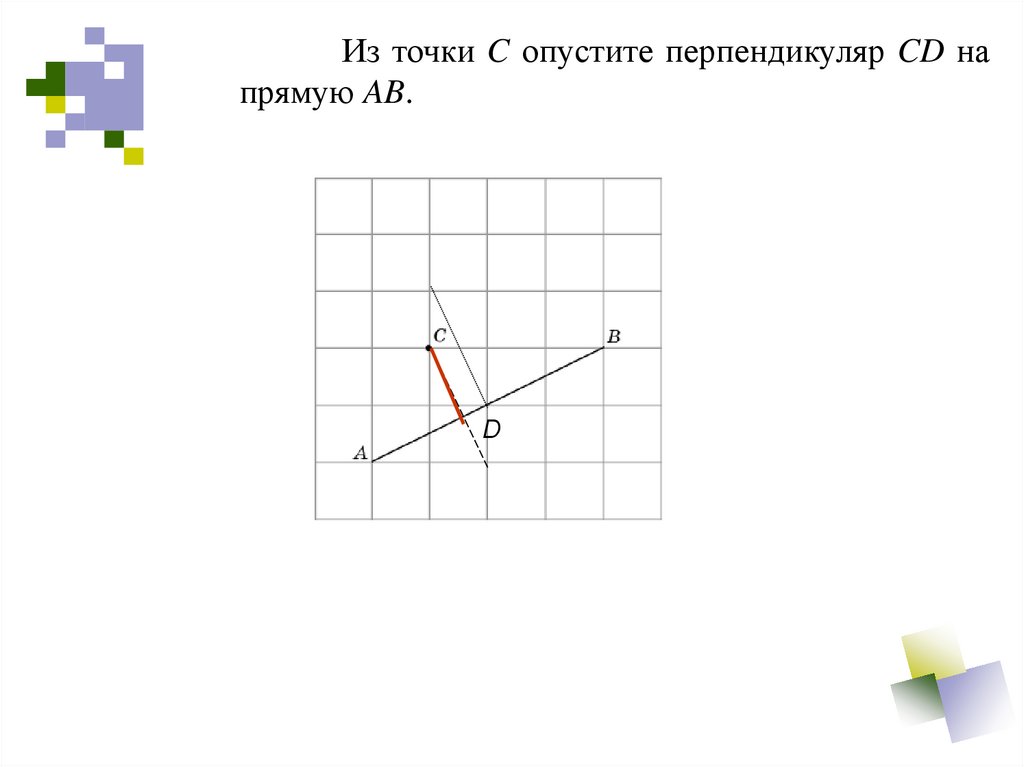
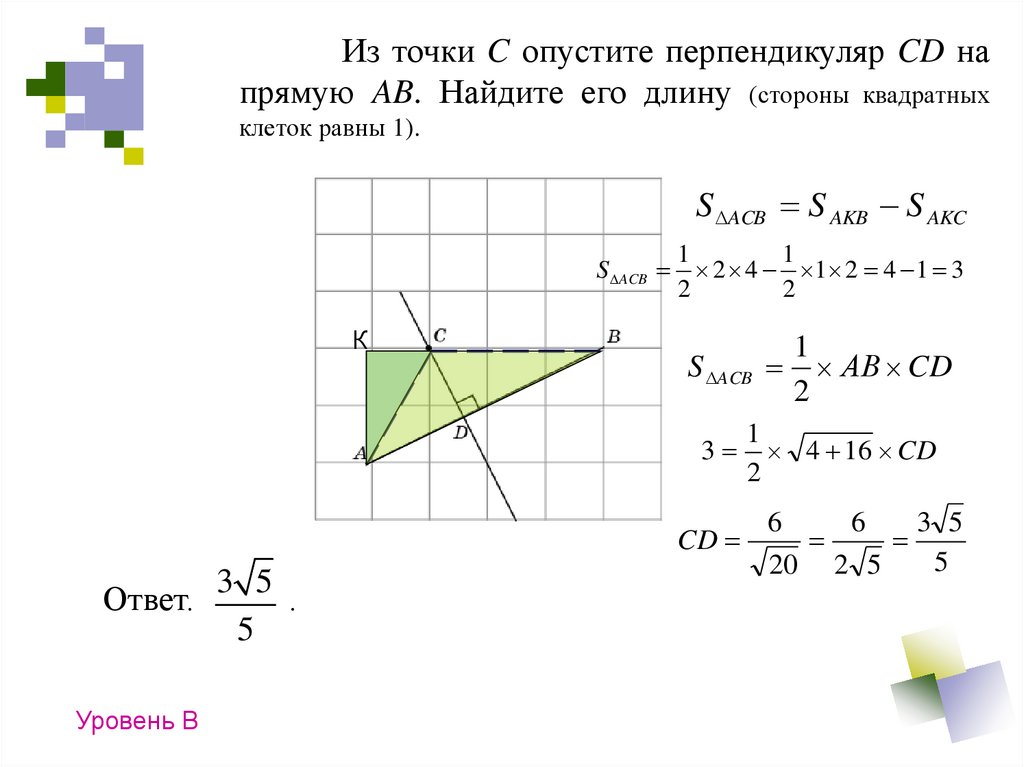
Из точки C опустите перпендикуляр CD на
прямую AB.
D

13.

Из точки C опустите перпендикуляр CD на
прямую AB. Найдите его длину (стороны квадратных
клеток равны 1).
S ACB S AKB S AKC
S ACB
1
1
2 4 1 2 4 1 3
2
2
К
S ACB
3
CD
3 5
Ответ.
.
5
Уровень В
1
АВ CD
2
1
4 16 CD
2
6
20
6
2 5
3 5
5

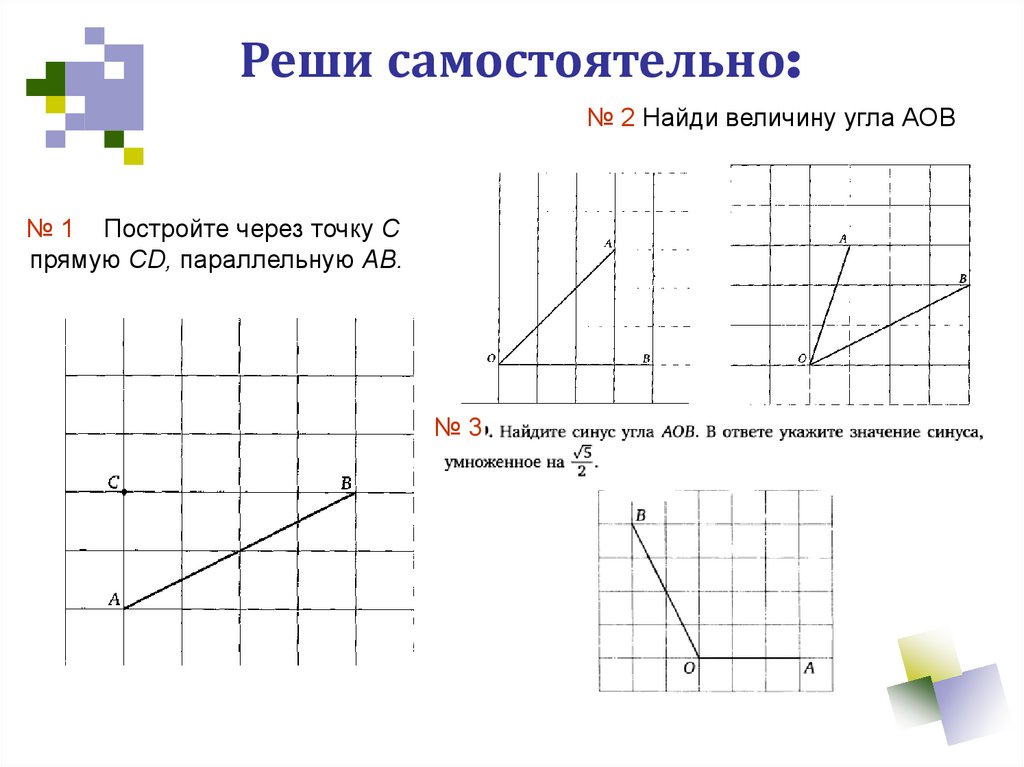
14.

Реши самостоятельно:
№ 2 Найди величину угла АОВ
№ 1 Постройте через точку C
прямую CD, параллельную AB.
№3

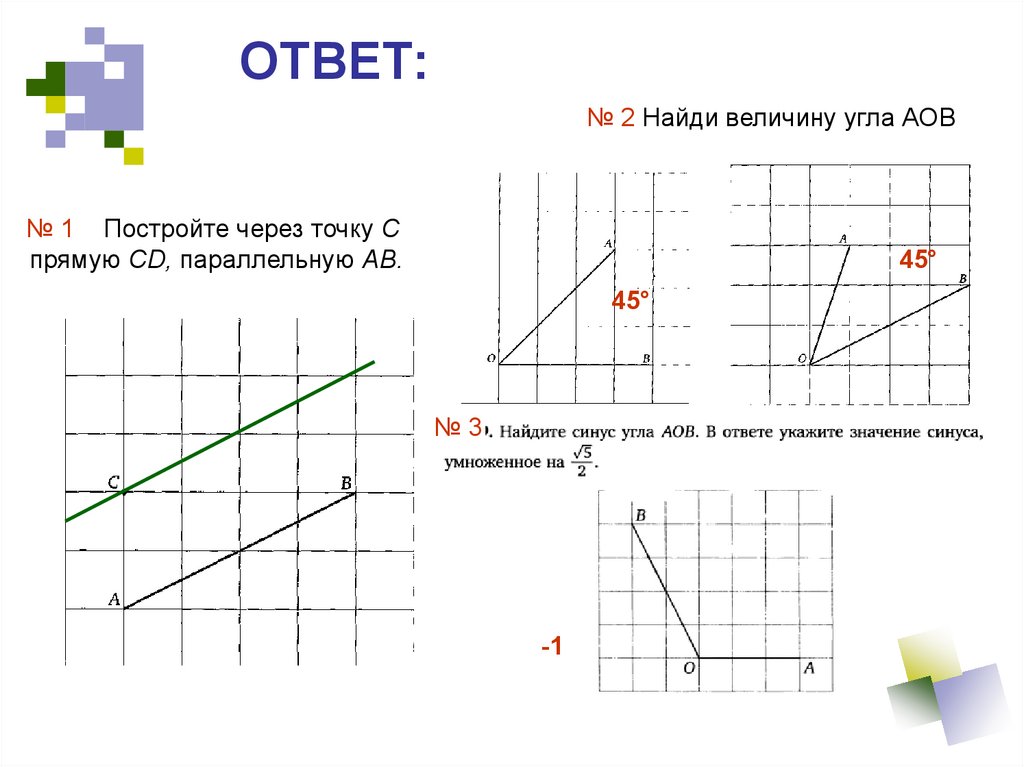
15.

ОТВЕТ:
№ 2 Найди величину угла АОВ
№ 1 Постройте через точку C
прямую CD, параллельную AB.
45°
45°
№3
-1

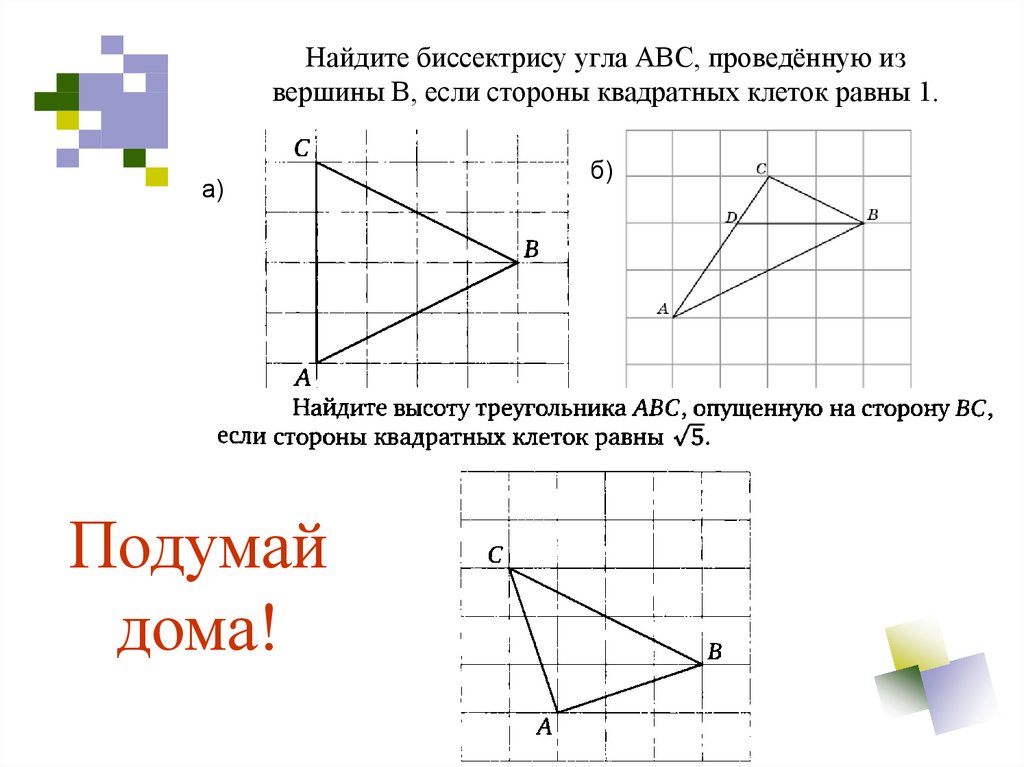
16. Найдите биссектрису угла АВС, проведённую из вершины В, если стороны квадратных клеток равны 1.

а)
Подумай
дома!
б)

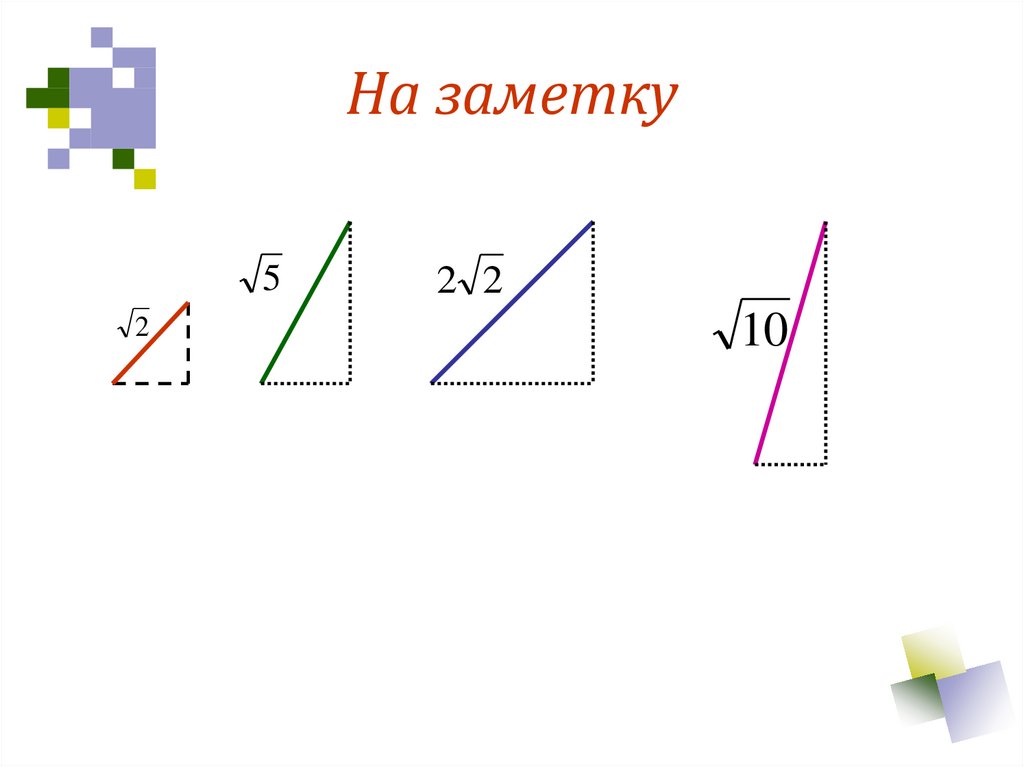
17. На заметку

5
2
2 2
10

18.

4
cos( AOB )
16 4
2
5
Ответ: 4
4
2 5
2 5 4
2
5

19.

sin( BOA )
1
2
3
3 2
2 2 2
Ответ: 2
1
2
3 2
3

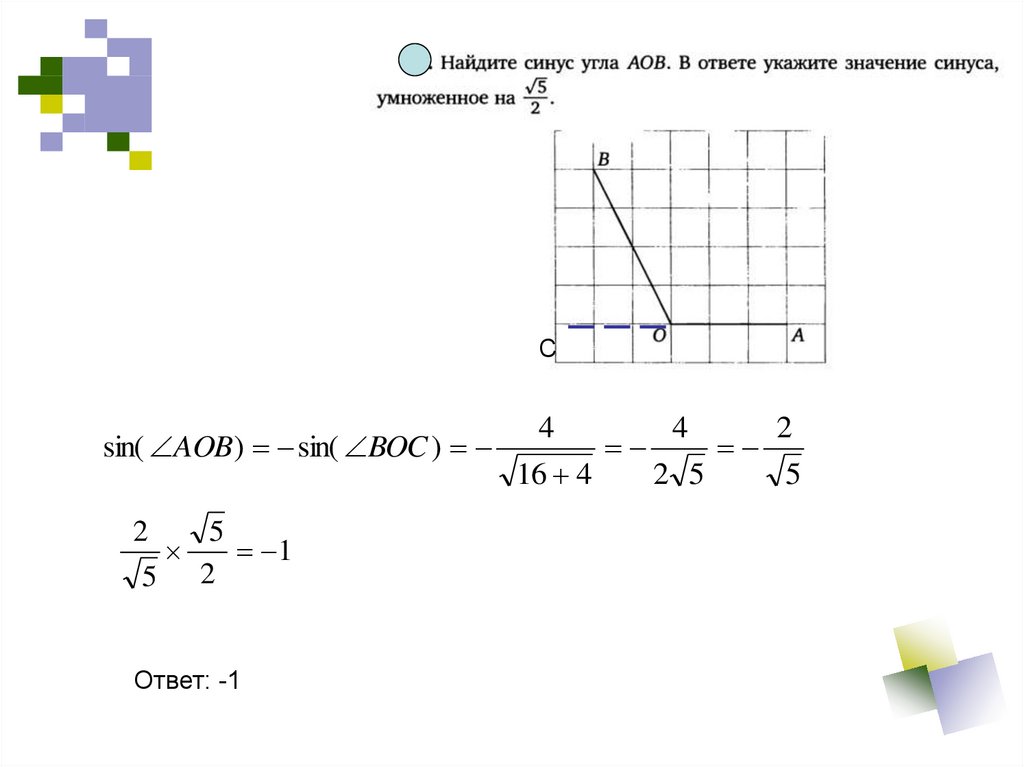
20.

С
sin( AOB ) sin( BOC )
2
5
5
1
2
Ответ: -1
4
16 4
4
2 5
2
5

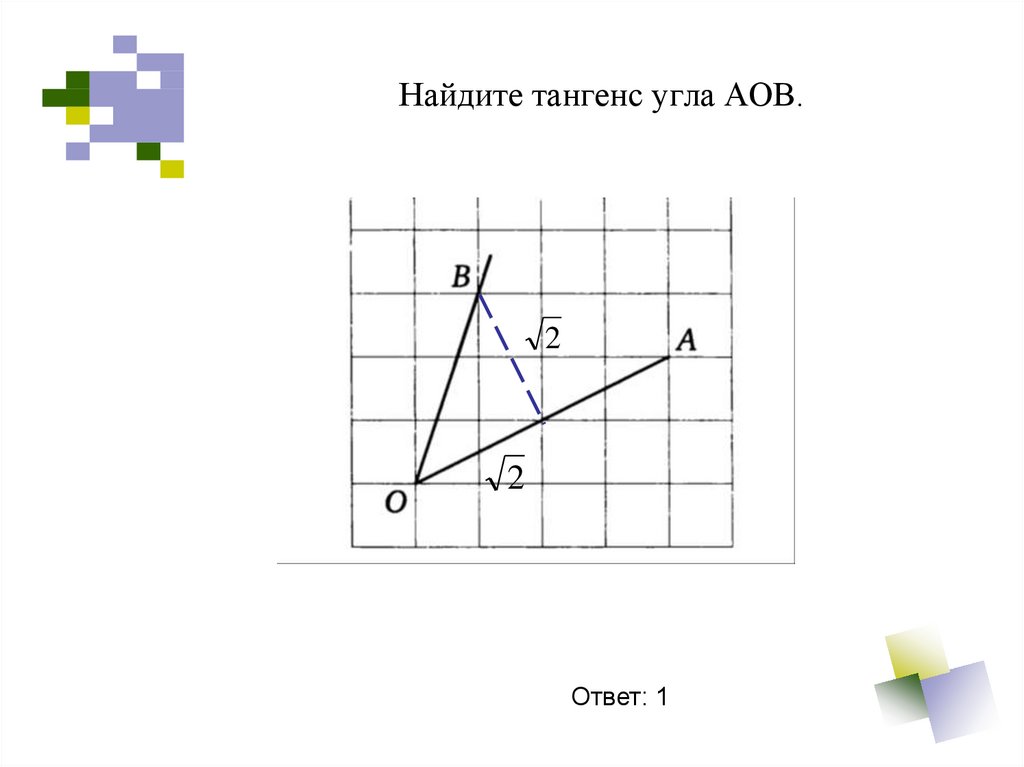
21. Найдите тангенс угла АОВ

Ответ: -2

22. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на .

Найдите синус угла АОВ. В ответе укажите
значение синуса, умноженное на 2 2 .
sin BOA
1
2
5
5
1
10
5 2
2
2 2 2
Ответ: 2

23. Найдите тангенс угла АОВ.

2
2
Ответ: 1

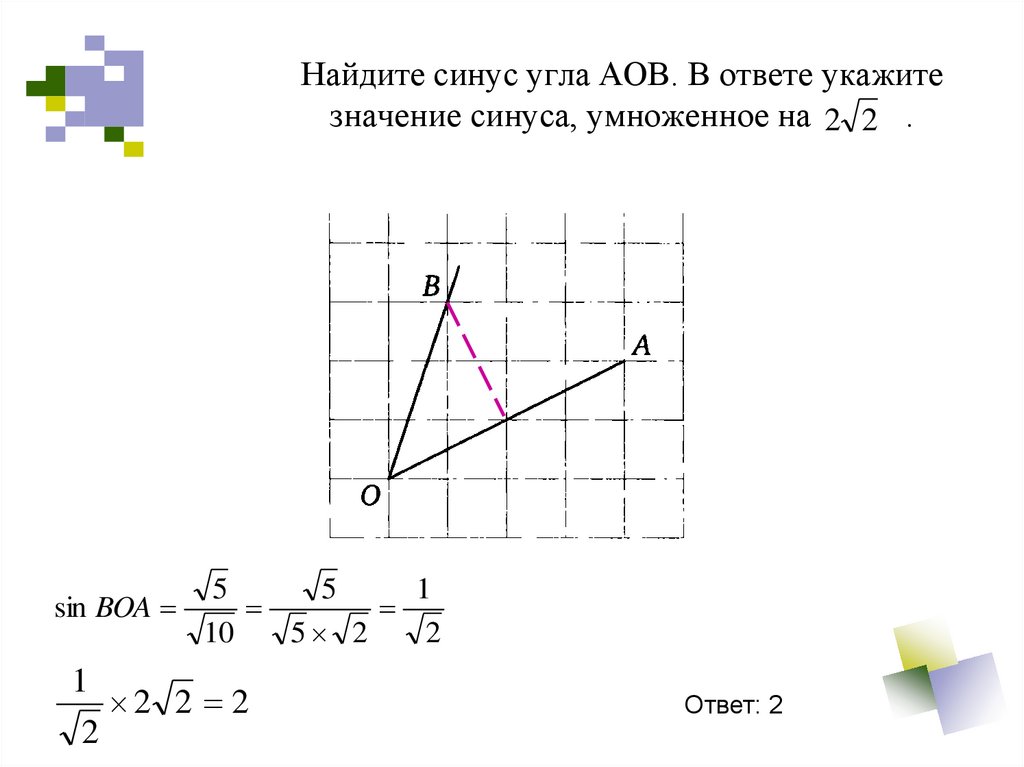
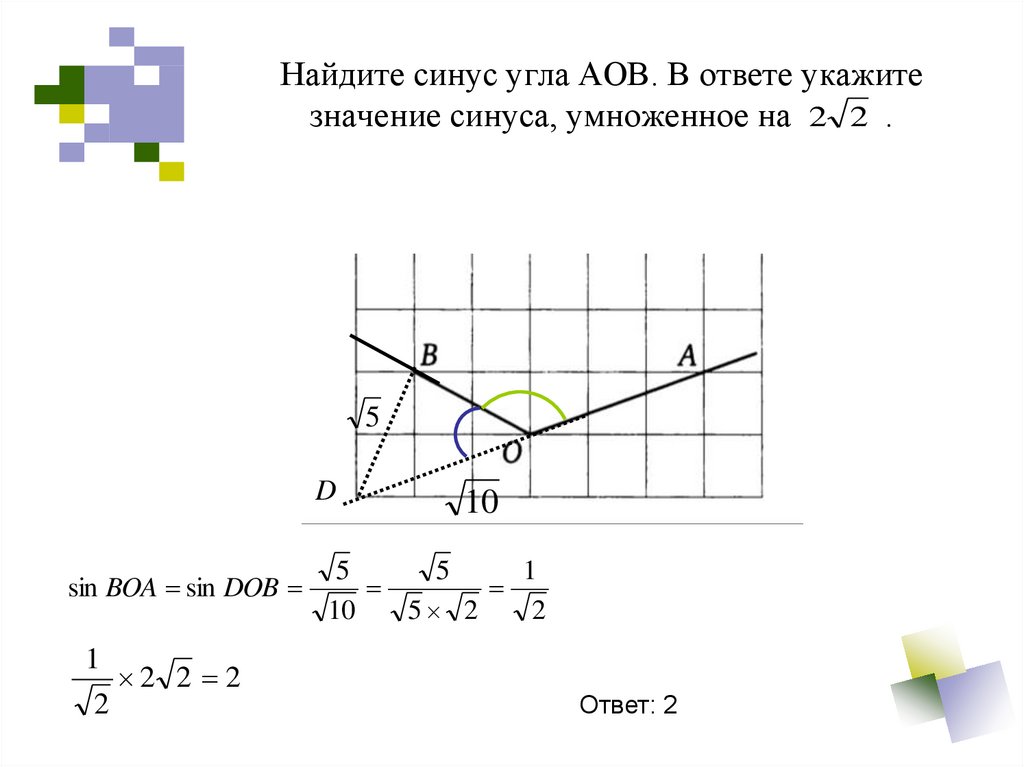
24. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на .

Найдите синус угла АОВ. В ответе укажите
значение синуса, умноженное на 2 2 .
5
D
sin BOA sin DOB
1
2
2 2 2
10
5
5
1
10
5 2
2
Ответ: 2

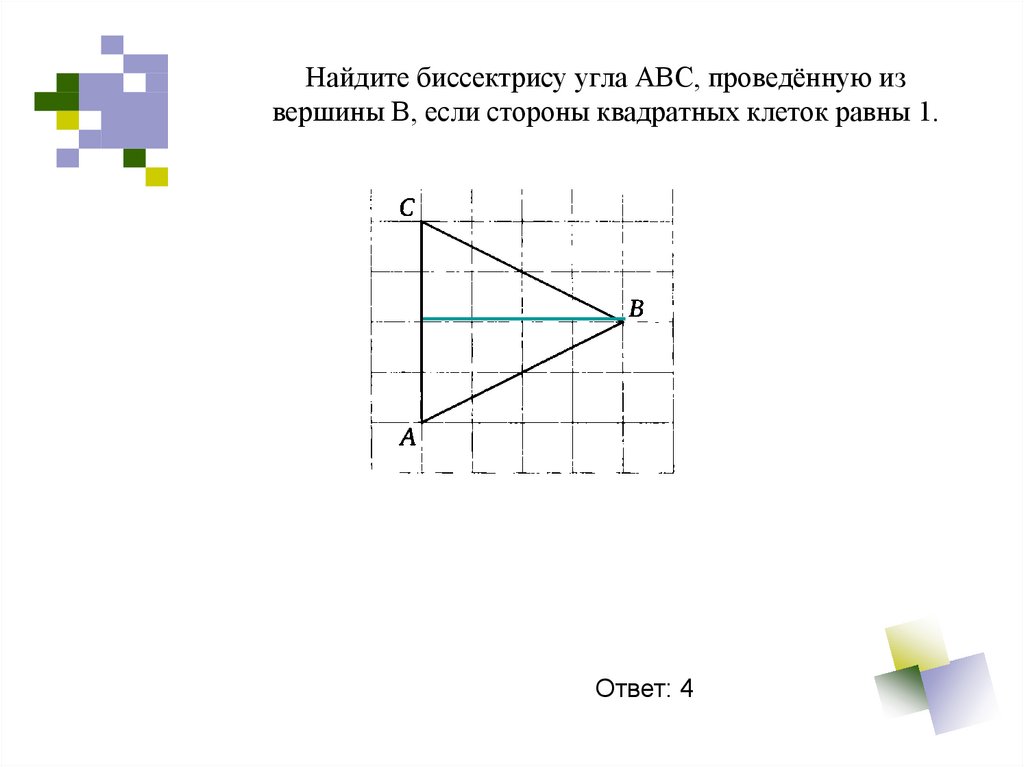
25. Найдите биссектрису угла АВС, проведённую из вершины В, если стороны квадратных клеток равны 1.

Ответ: 4

26.

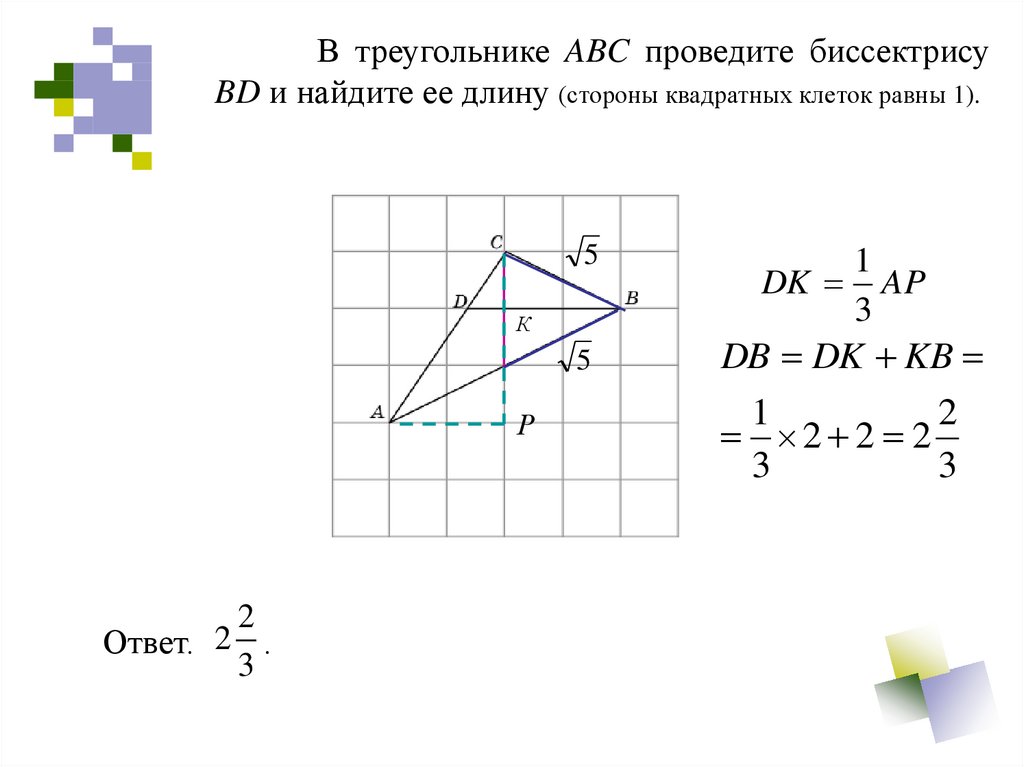
В треугольнике ABC проведите биссектрису
BD и найдите ее длину (стороны квадратных клеток равны 1).
5
К
5
Р
2
2
Ответ.
.
3
1
DK AP
3
DB DK KB
1
2
2 2 2
3
3

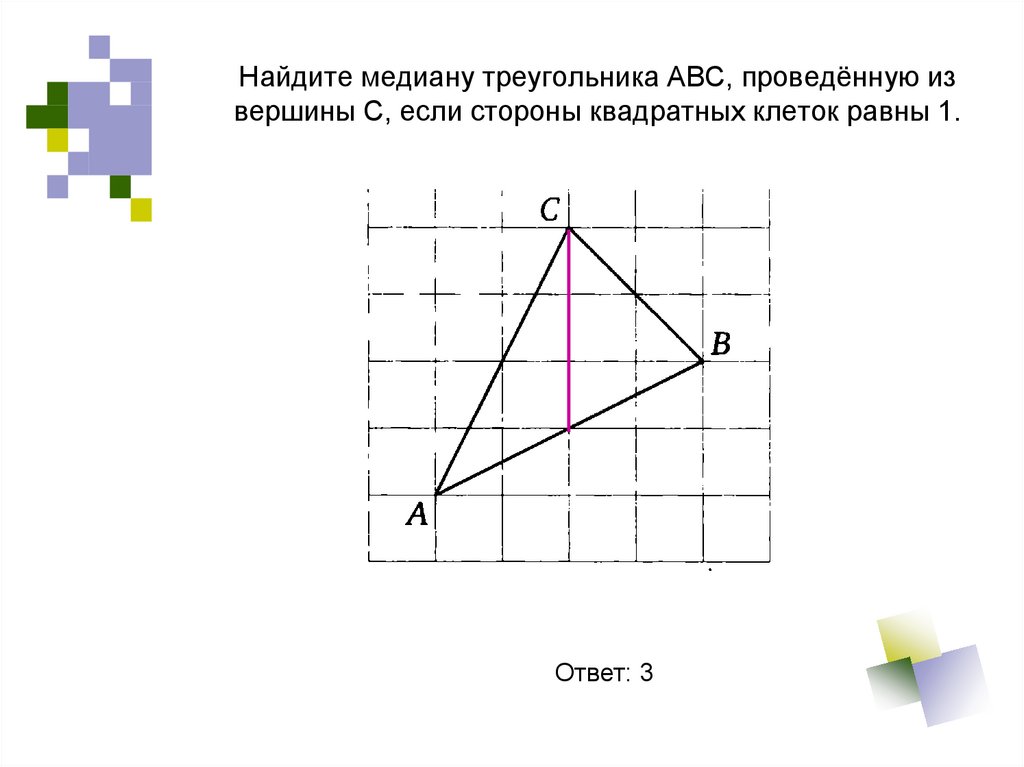
27. Найдите медиану треугольника АВС, проведённую из вершины С, если стороны квадратных клеток равны 1.

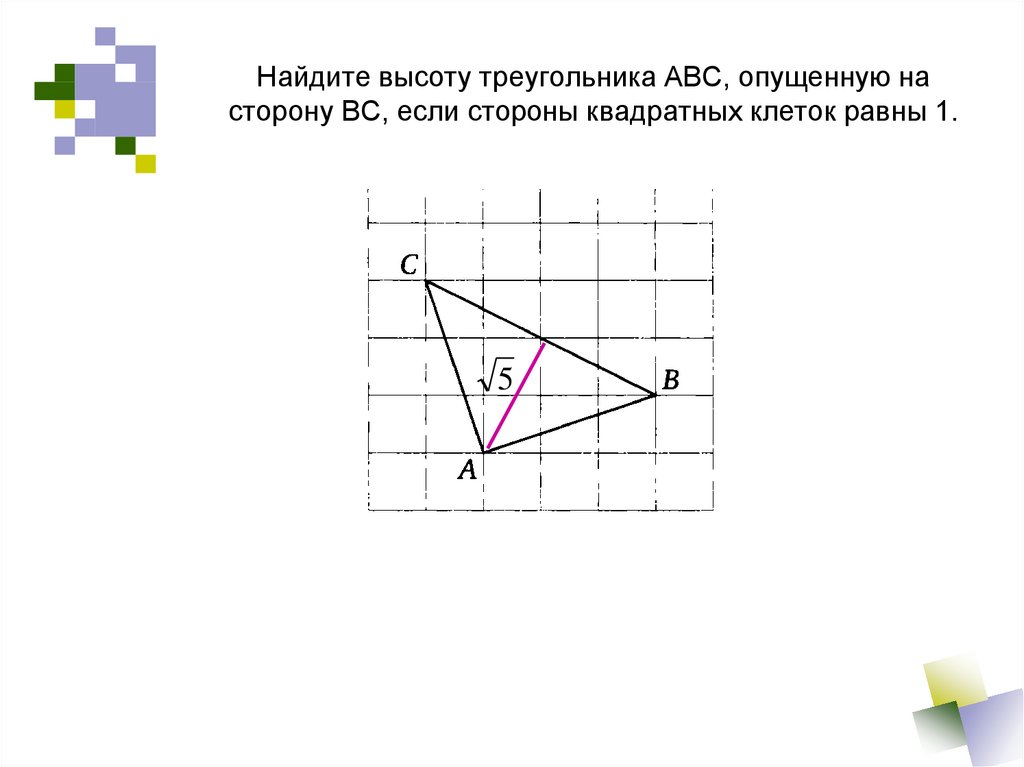
Ответ: 3

28. Найдите высоту треугольника АВС, опущенную на сторону ВС, если стороны квадратных клеток равны 1.

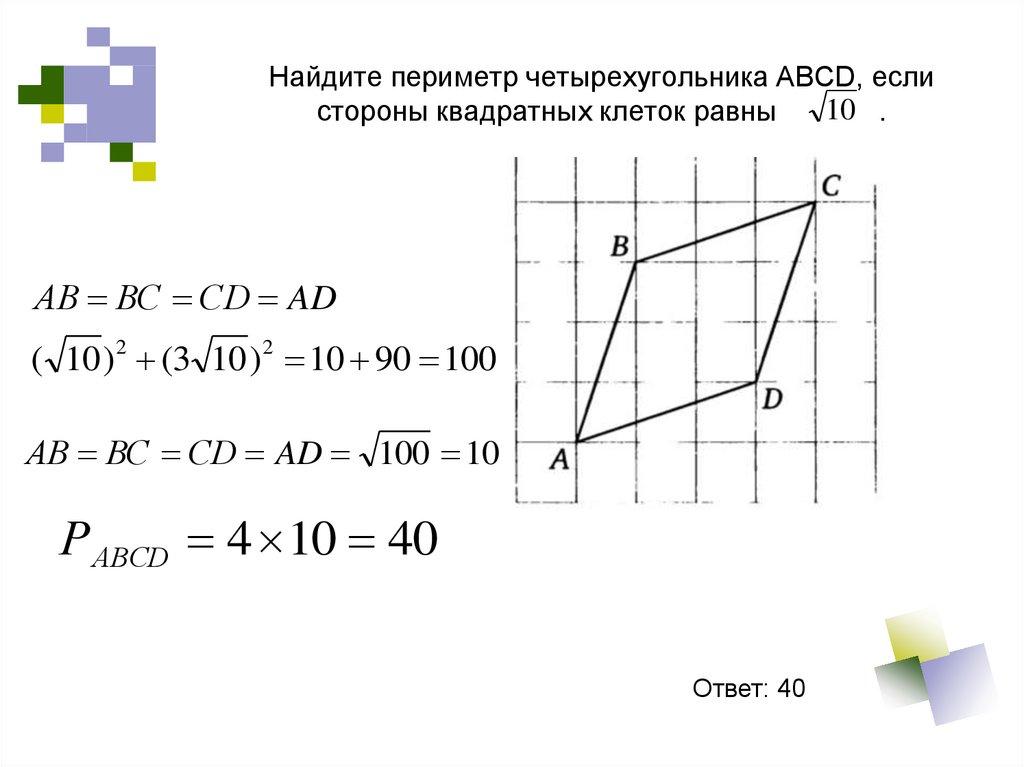
5

29. Найдите периметр четырехугольника АВСD, если стороны квадратных клеток равны .

Найдите периметр четырехугольника АВСD, если
10 .
стороны квадратных клеток равны
АВ ВС СD AD
( 10 )2 (3 10 )2 10 90 100
АВ ВС СD AD 100 10
Р АВСD 4 10 40
Ответ: 40

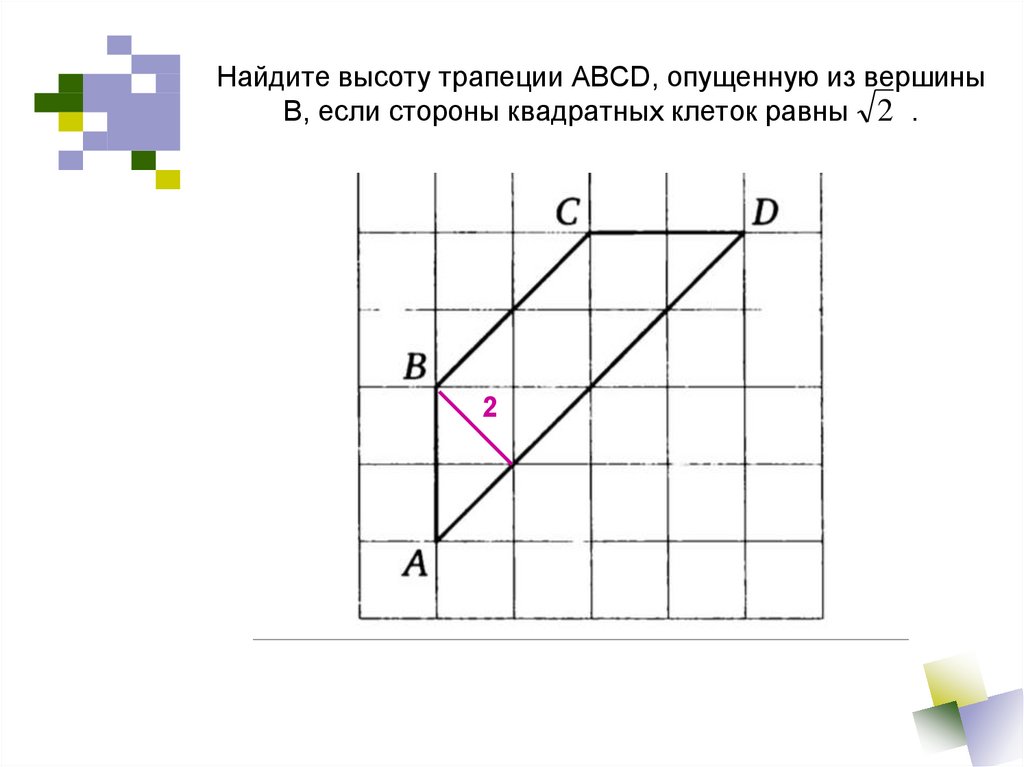
30. Найдите высоту трапеции ABCD, опущенную из вершины В, если стороны квадратных клеток равны .

Найдите высоту трапеции ABCD, опущенную из вершины
В, если стороны квадратных клеток равны 2 .
2

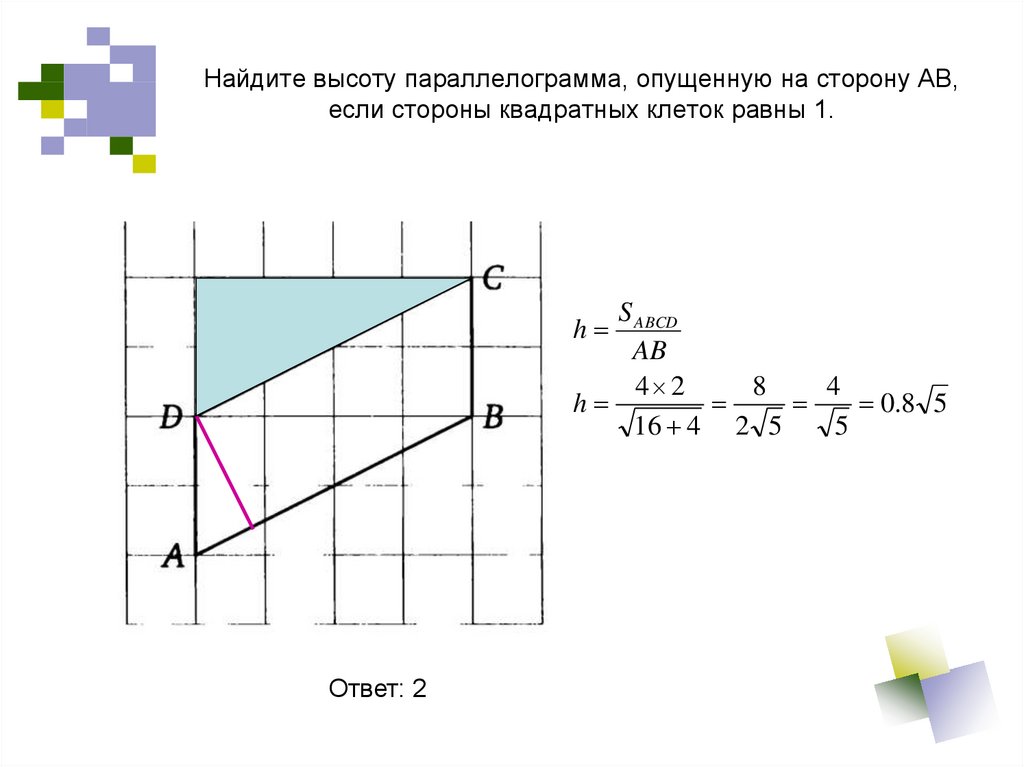
31. Найдите высоту параллелограмма, опущенную на сторону АВ, если стороны квадратных клеток равны 1.

S ABCD
AB
4 2
8
4
h
0.8 5
16 4 2 5
5
h
Ответ: 2

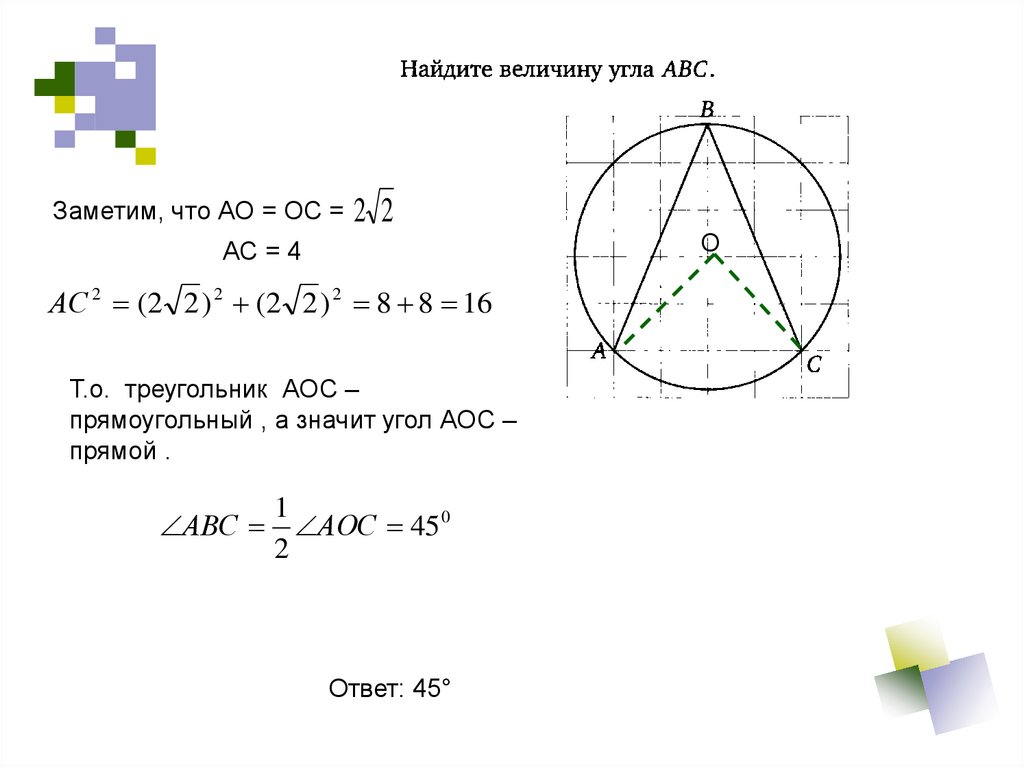
32.

Заметим, что АО = ОС =
2 2
АС = 4
АС 2 (2 2 ) 2 (2 2 ) 2 8 8 16
Т.о. треугольник АОС –
прямоугольный , а значит угол АОС –
прямой .
1
АВС АОС 45 0
2
Ответ: 45°
О

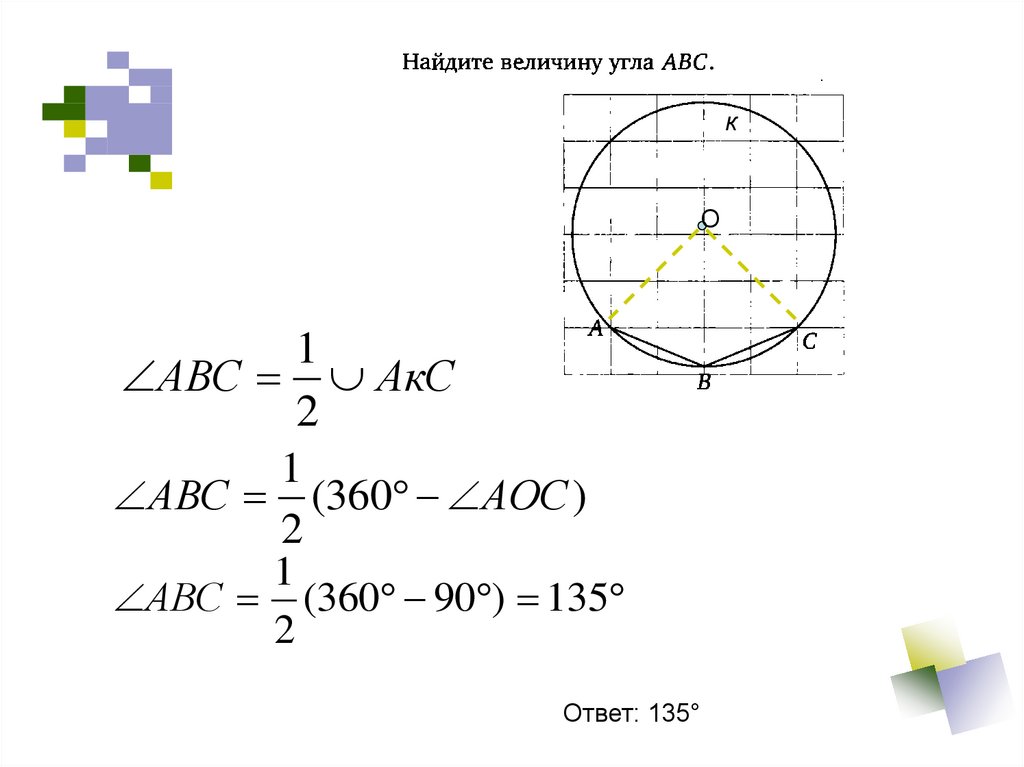
33.

к
О
1
АВС АкС
2
1
АВС (360 АОС )
2
1
АВС (360 90 ) 135
2
Ответ: 135°

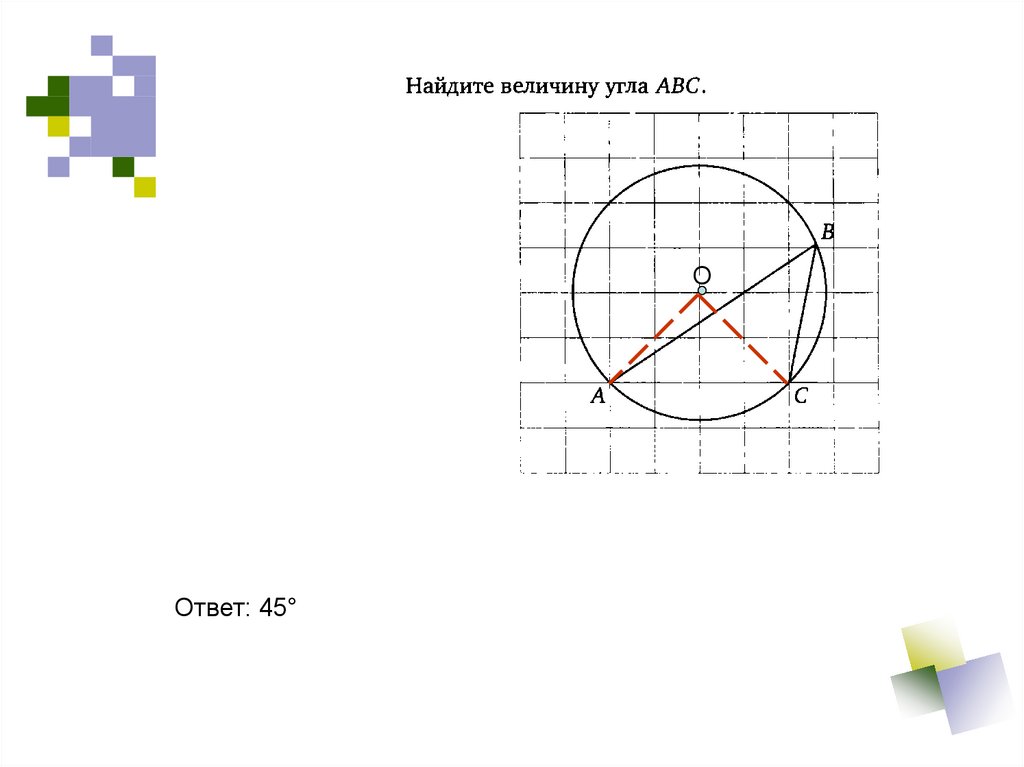
34.

О
Ответ: 45°

35.

Уровень С

36.

Уровень С

37.

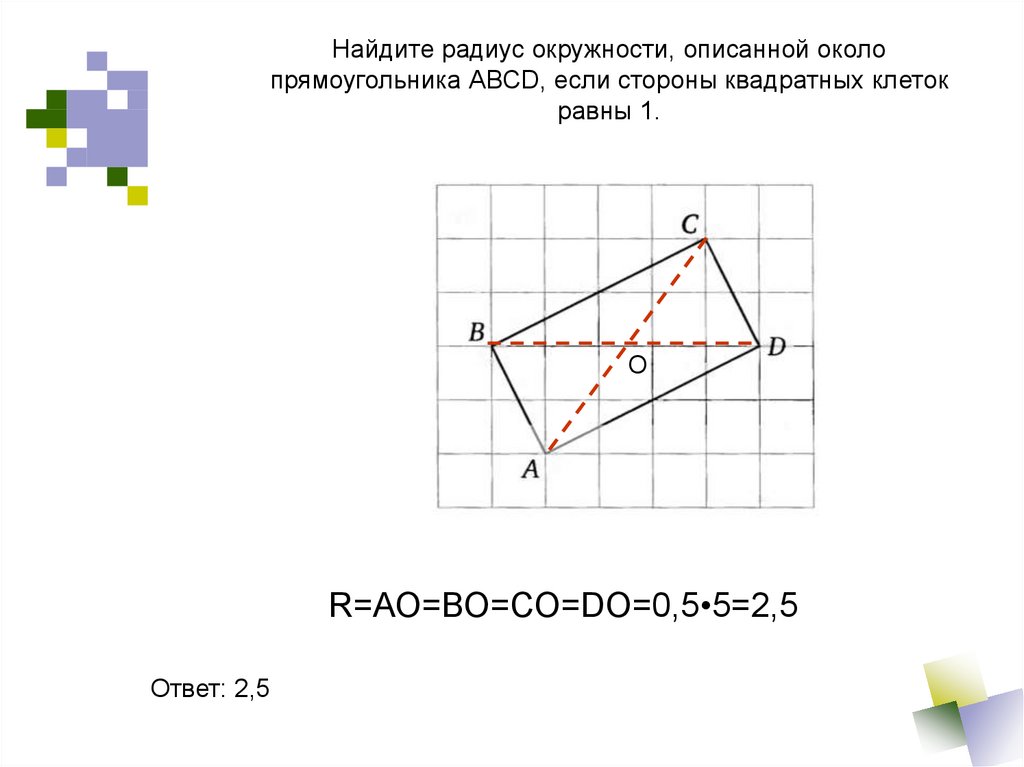
Найдите радиус окружности, описанной около
прямоугольника АВСD, если стороны квадратных клеток
равны 1.
О
R=АО=ВО=СО=DO=0,5•5=2,5
Ответ: 2,5

38.

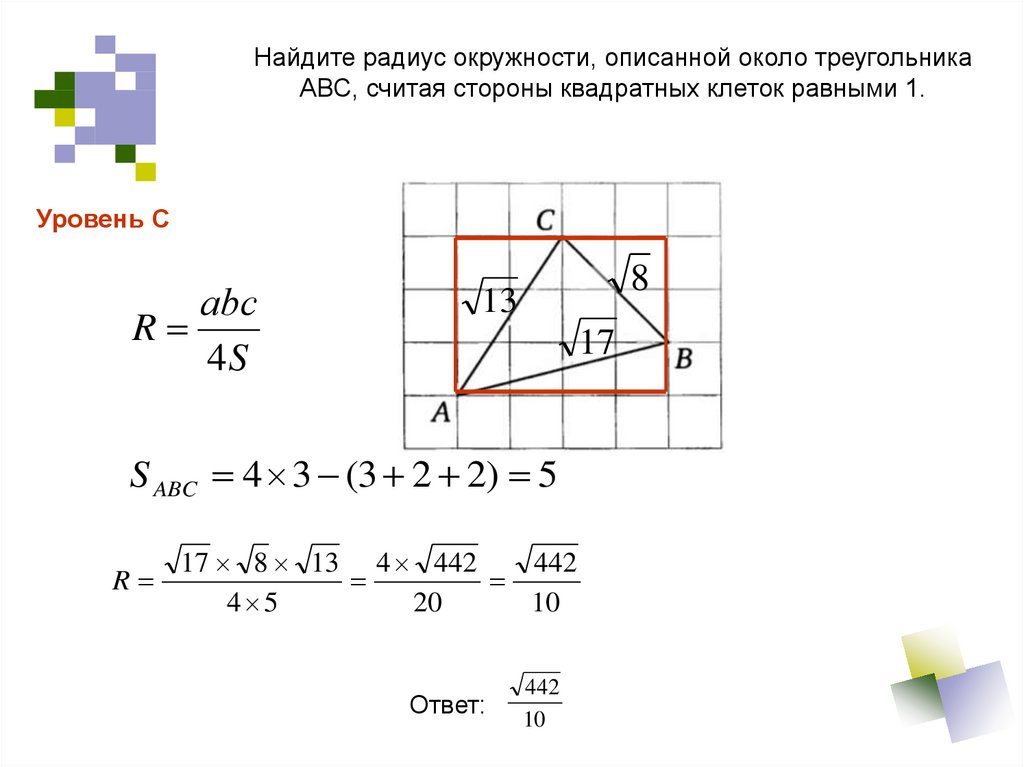
Найдите радиус окружности, описанной около треугольника
АВС, считая стороны квадратных клеток равными 1.
Уровень С
аbс
R
4S
8
13
17
S ABC 4 3 (3 2 2) 5
R
17 8 13 4 442
442
4 5
20
10
Ответ:
442
10

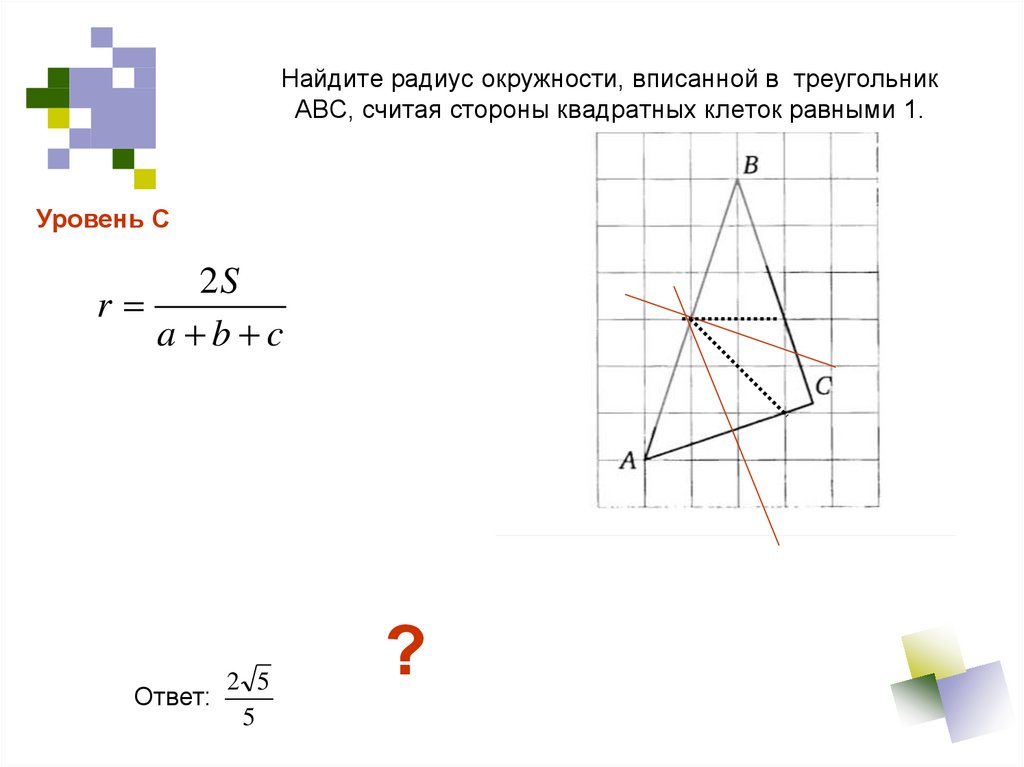
39. Найдите радиус окружности, вписанной в треугольник АВС, считая стороны квадратных клеток равными 1.

Уровень С
2S
r
a b c
2 5
Ответ:
5
?

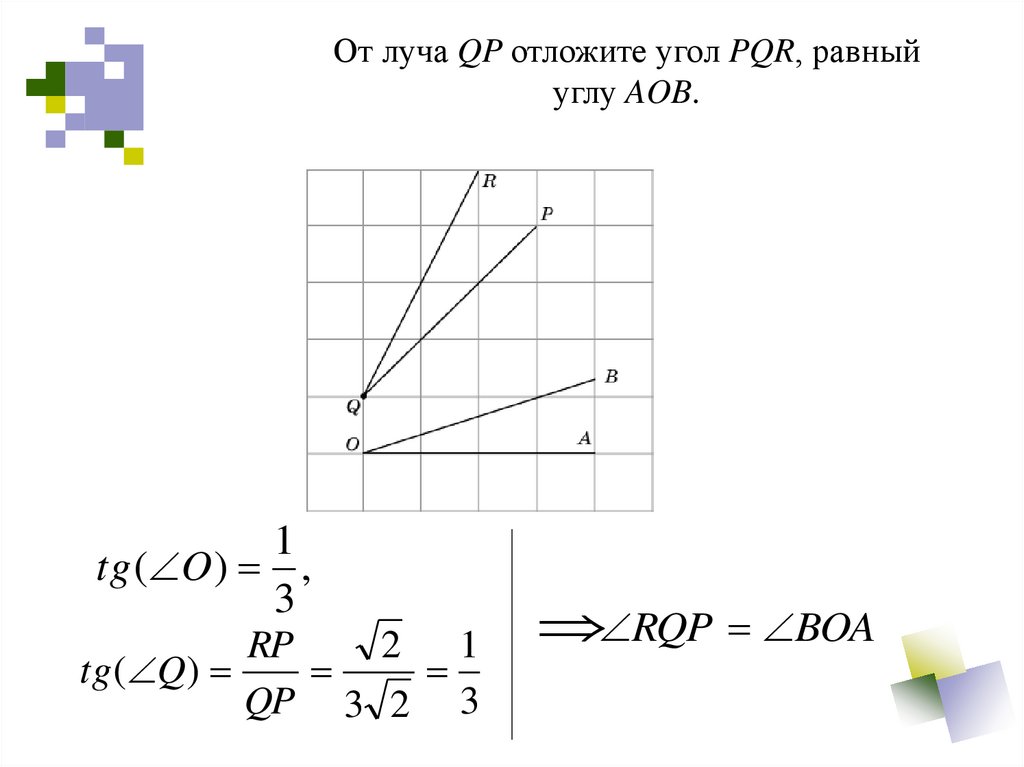
40.

От луча QP отложите угол PQR, равный
углу AOB.
1
tg ( O ) ,
3
RP
2 1
tg ( Q)
QP 3 2 3
RQP BOA