Похожие презентации:
Геометрия «на клетчатой бумаге»
1. Геометрия «на клетчатой бумаге»
Павлова Наталья ВалерьевнаУчитель математики
МОУ «Лицей №6»
2. теорема Пифагора, соотношения между сторонами и углами в прямоугольном треугольнике, свойства всех плоских фигур, изучаемых в
• При решении задач с использованиемклетчатой бумаги важно помнить, что
«клеточки» должны помогать! А значит,
нужно подумать как они могут помочь. По
«клеточкам» легко построить
прямоугольный треугольник.
Следовательно, могут помочь все
теоретические факты связанные с
прямоугольным треугольником.
• Решение таких задач не предполагает
использование циркуля и линейки, а
осуществляется непосредственно на
рисунке клетчатой бумаги.
теорема Пифагора,
соотношения между сторонами и углами в
прямоугольном треугольнике,
свойства
всех плоских фигур, изучаемых в школе.
3.
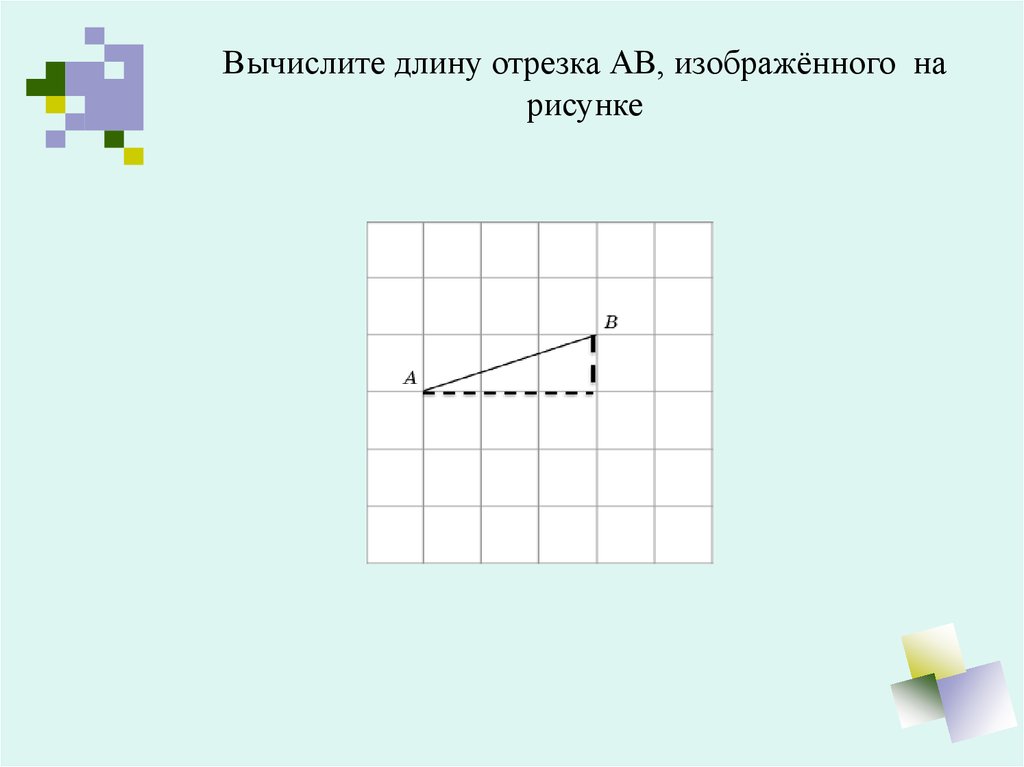
Вычислите длину отрезка АВ, изображённого нарисунке
4.
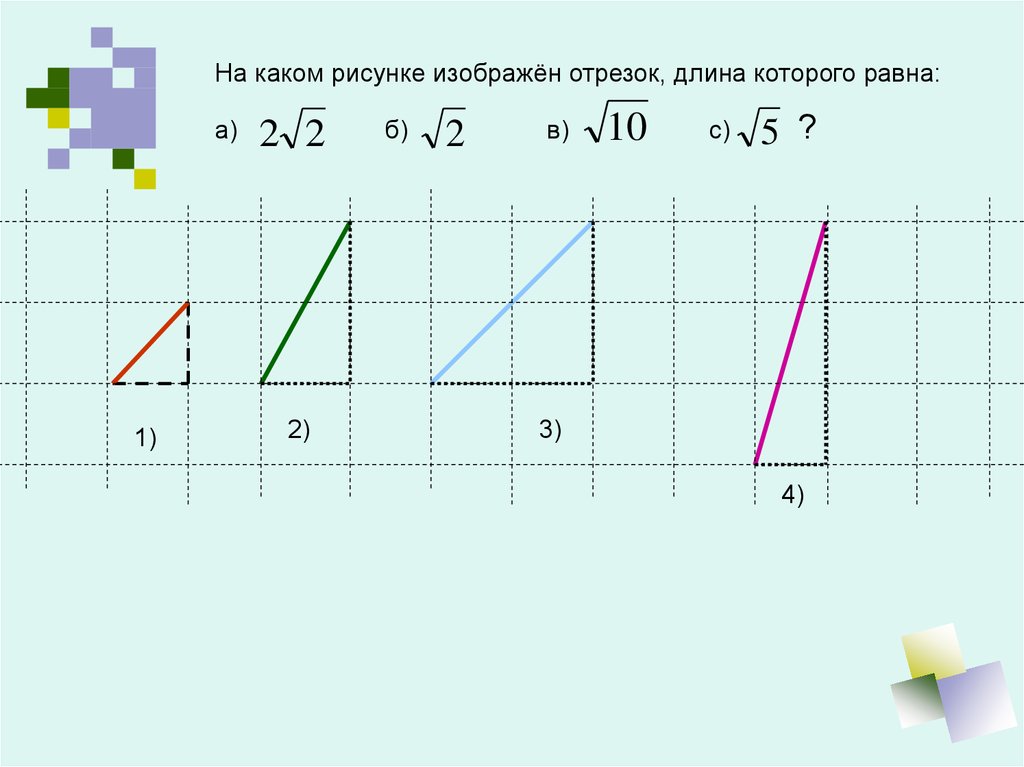
На каком рисунке изображён отрезок, длина которого равна:а)
1)
2 2
2)
б)
2
в)
10
с)
5 ?
3)
4)
5. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на
2 2sin BOA
В
sin BOA
1
2
3
О
F
Ответ: 2
BF
BO
А
BF
3
1
BO
3 2
2
2 2 2
6. Найдите тангенс угла АОВ.
В4
О
2
Ответ: 2
А
7.
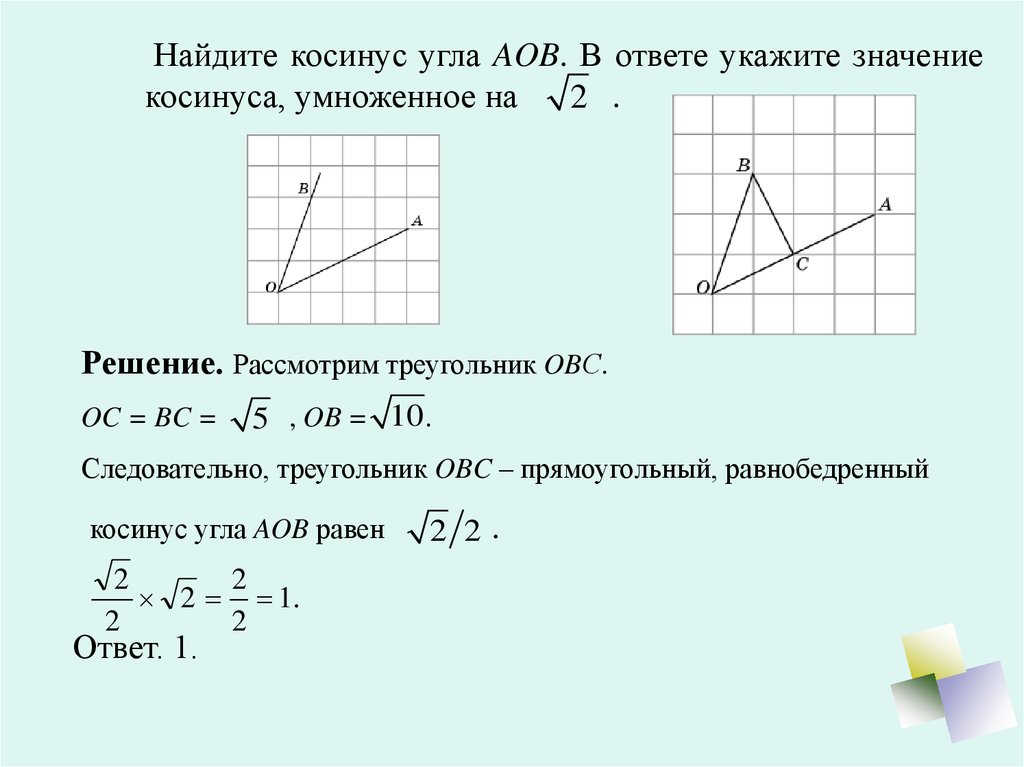
Найдите косинус угла AOB. В ответе укажите значениекосинуса, умноженное на
2 .
Решение. Рассмотрим треугольник OBС.
OC = BC =
5 , OB = 10 .
Следовательно, треугольник OBC – прямоугольный, равнобедренный
косинус угла AOB равен
2
2
2 1.
2
2
Ответ. 1.
2 2.
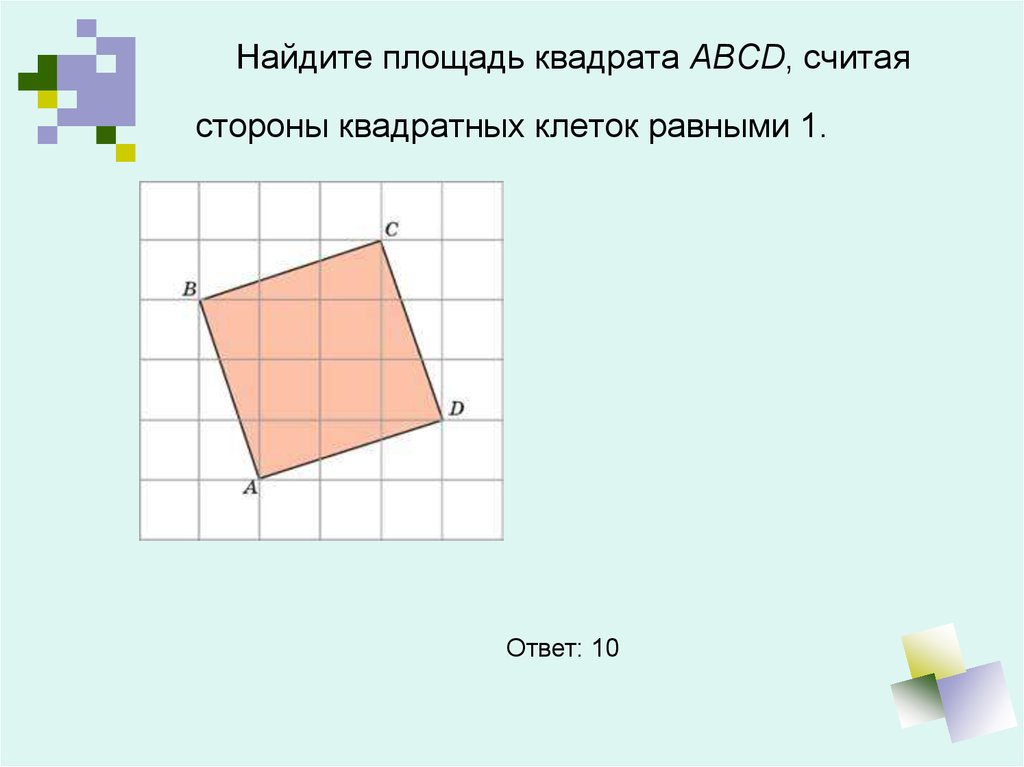
8. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1.
Ответ: 109. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Ответ: 1010. Найдите площадь фигуры, изображённой на рисунке
1( a b) h
2
В нашем случае а = AD, b = BC, h = CD
1 способ
AD
42 22
CD BC
S трап
2 способ
S11
S
S2
SS2
2
S4
S3
S трап
20 2 5 (см);
12 2 2
5 (см)
1
1
(2 5 5 ) 5 3 5 7,5(см 2 )
2
2
S трап S кв ( S1 2S 2 S3 S 4 )
1
1
1
4 (1 2 2 1 4 2 3 1)
2
2
2
16 (1 2 4 1,5) 7,5(см 2 )
2
2
Ответ: 7,5
11. Найдите площадь треугольника, изображённого на рисунке, считая длину стороны клетки, равной 1 см.
25 16 414 36 40
S Sкв (S1 S2 S3 )
1 36 37
Ответ: 17
S 36 (10 6 3) 17
12.
Заметим, что АО = ОС =2 2
АС = 4
АС 2 (2 2 ) 2 (2 2 ) 2 8 8 16
Т.о. треугольник АОС –
прямоугольный , а значит угол АОС –
прямой .
1
АВС АОС 45 0
2
Ответ: 45°
О
13.
14.
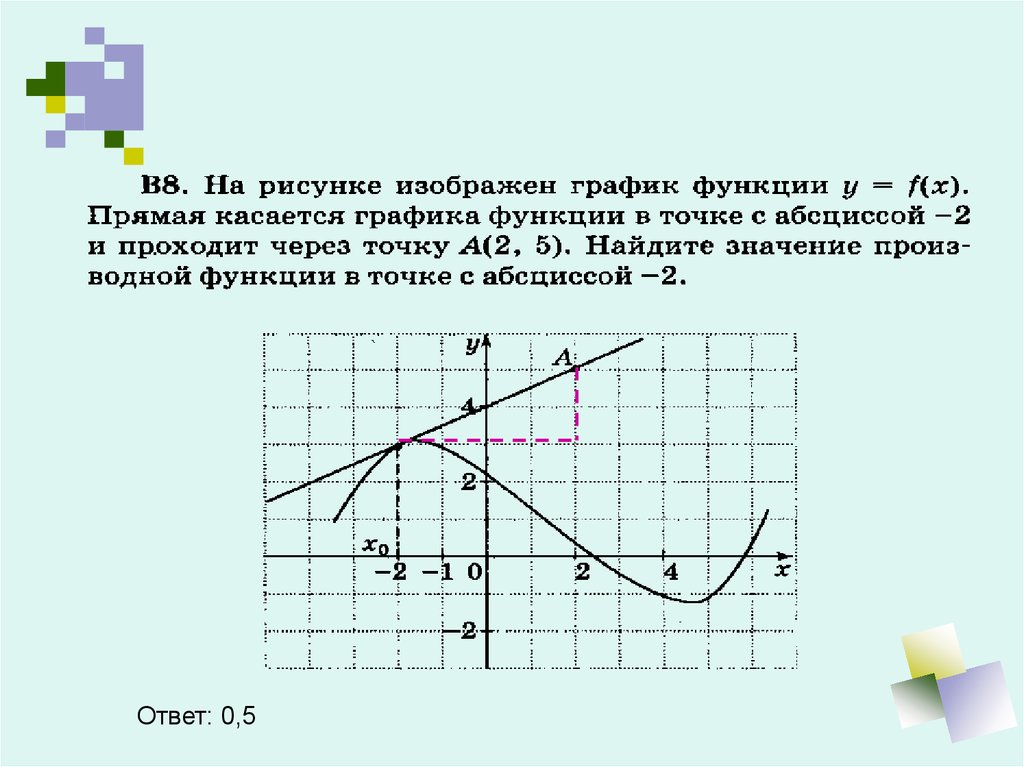
Ответ: 0,515.
Ответ: -0,516.
Ответ: - 0,517.
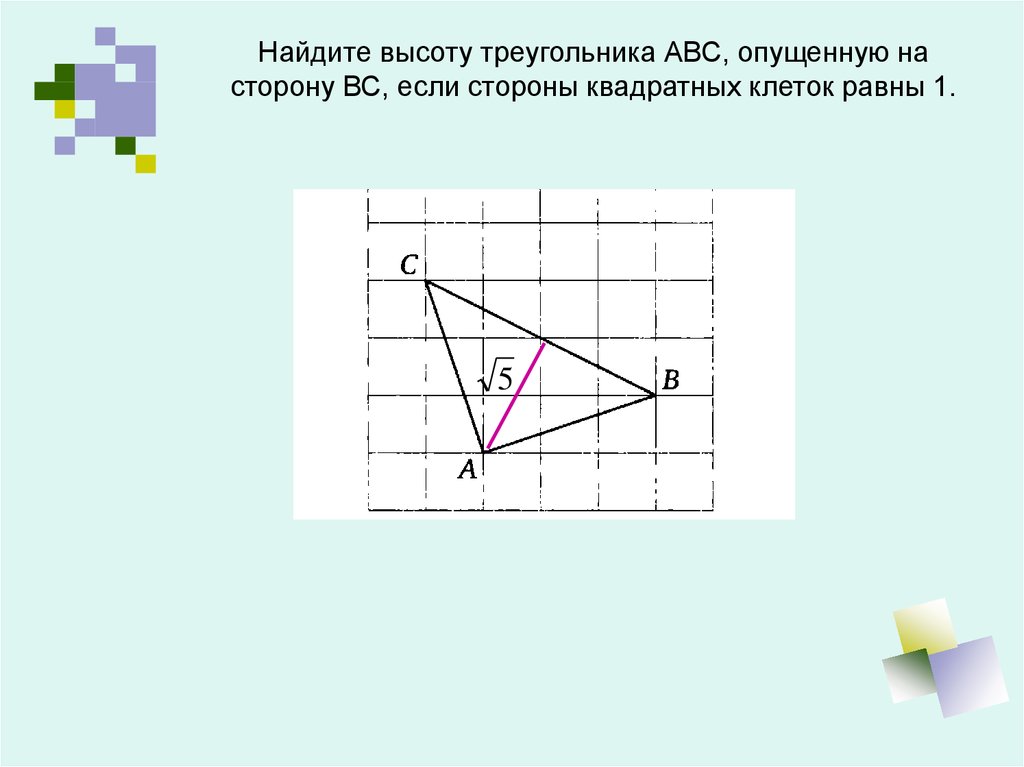
Найдите высоту треугольника АВС, опущенную насторону ВС, если стороны квадратных клеток равны 1.
5
18.
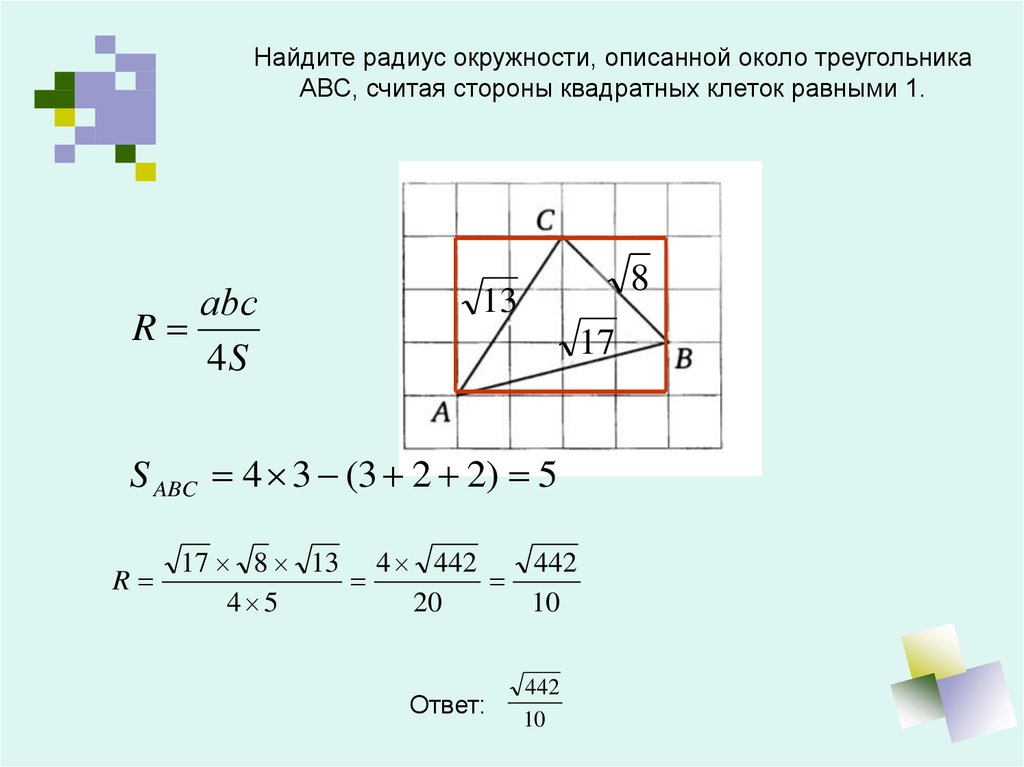
Найдите радиус окружности, описанной около треугольникаАВС, считая стороны квадратных клеток равными 1.
аbс
R
4S
8
13
17
S ABC 4 3 (3 2 2) 5
R
17 8 13 4 442
442
4 5
20
10
Ответ:
442
10












 Математика
Математика








