Похожие презентации:
Объем конуса
1. Объем конуса
2. Сократ (470 – 380 гг. до н. э.)
« Пусть сюдане входит
никто,
не знающий
геометрии».
3. Содержание
Повторение основных сведений о конусе.Историческая справка.
Новый материал.
Решение задач с применением формул
объема конуса.
Дополнительные сведения о конусе.
Конические формы в профессии.
4. Повторение.
1.Определение конуса.2.Основные характеристики конуса.
3.Вращением какой фигуры получается
конус, усеченный конус.
5. Историческая справка
Конус в переводе с греческого означает«сосновая шишка». С конусом люди
знакомы с глубокой древности. В 1906 г.
Была обнаружена книга Архимеда «О
методе»,в которой дается решение задачи
об объеме общей части пересекающихся
цилиндров. Архимед приписывает честь
открытия этого принципа Демокриту ( 470380г. До н. э.) Он получил формулы для
объема пирамиды и конуса.
6. Примеры конусообразных форм из различных профессий.
Игла для вышиванияНаперстки
Игла для вышивания
Наперстки
7. Практическое применение
8. Практическое применение
9. Дополнительные сведения о конусе.
1. «Конусами» называется семействоморских молюсков.
2. В геологии существует понятие «конус
выноса» вынесение породы горными
реками.
3. В биологии есть понятие «конус
нарастания» Это верхушка побега.
4. Громоотводы создают вокруг себя «конус
безопасности» Чем выше громоотвод,
тем больше объем такого конуса.
10. Новый материал
HV
S
(
x
)
dx
кон .
V
limV пир.
кон .
0
n
1
V кон. 3
R
2
H
11. Доказательство 1
HS
(
x
)
dx
V кон.
H
x
0
S(x)
1
2
H
V кон. 3 R
12. Доказательство 2
VV тела 0 f x dx
H
кон ..
2
0 kx dx
H
1
V кон. 3
2
R
2
y=kx
H
O
R
X
13. Доказательство 3
1V кон. lim V пир. lim S осн. H
n
n 3
1
1
H lim S осн. H S круга
3
3
1
2
V кон. 3 R H
14. Новый материал.
15. Подведение итогов
1V кон. 3
R
R – радиус основания
H – высота конуса
2
H
16. Решение задачи №1
Найдите объем тела, полученного при вращениипрямоугольного треугольника с катетом 6 см и
гипотенузой 10 см вокруг большего катета.
Решение:
А
Найдем неизвестный катет, т. к. он
будет большим, то вращение
происходит вокруг него. Это и
будет высота конуса.
10см
С
6см
Ответ:288 см.
В
17. Задача №2
Смолу дляпромышленных нужд
собирают, подвешивая
конические воронки к
соснам. Сколько надо
воронок диаметром
10см и с образующей
13см, чтобы заполнить
ведро объемом 10
литров.
Ответ: примерно 32 воронки.
18. Историческая задача
.Рассчитаем высоту холма о котором
говорится в поэме А. С. Пушкина «Скупой
рыцарь»: 1 горсть земли примерно 0,2 дм2
Войско в 100000 воинов считалось очень
большим. Угол откоса примерно 450
Найдем высоту холма.
Ответ: Н= 2,7 м.
19. Решить дома:
У Аттилы, вождя гунов, было самоебольшое войско около 700 000 человек.
Попробуйте рассчитать высоту холма,
насыпанного войском Аттилы.









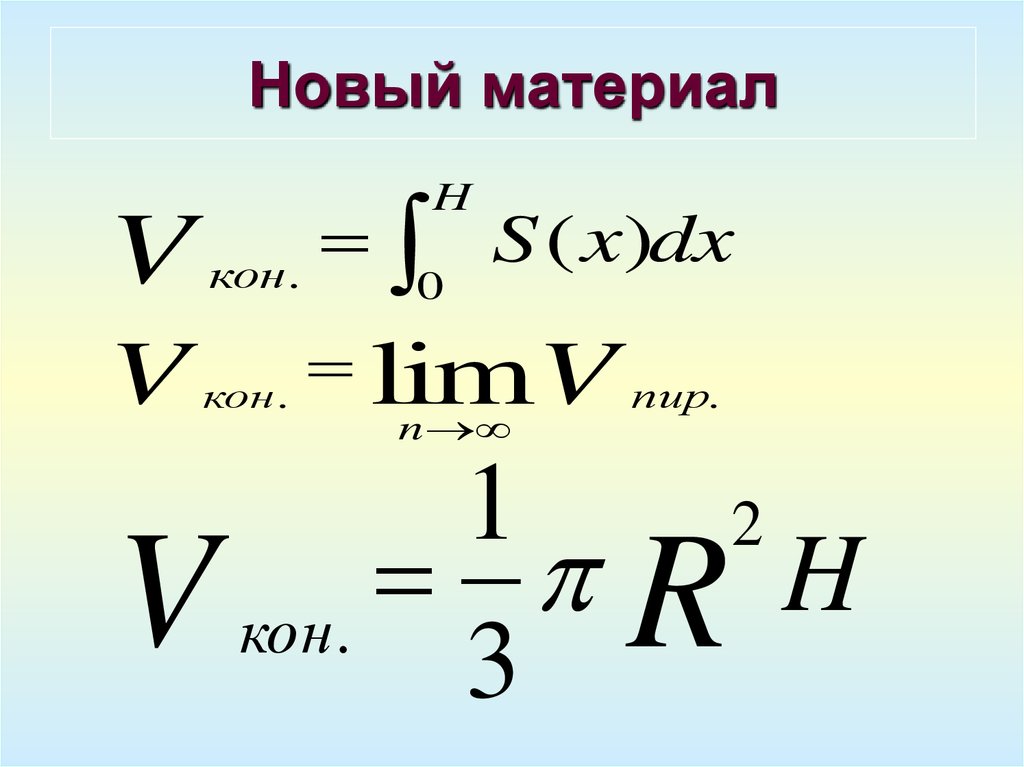










 Математика
Математика








