Симметрия на плоскости

1. Симметрия на плоскости

Урок геометрии в 9 классе
Учитель : Лежнина Е.А.

2. Изучение нового материала

В геометрии существует
два вида симметрии
ОСЕВАЯ
симметрия
ЦЕНТРАЛЬНАЯ
симметрия

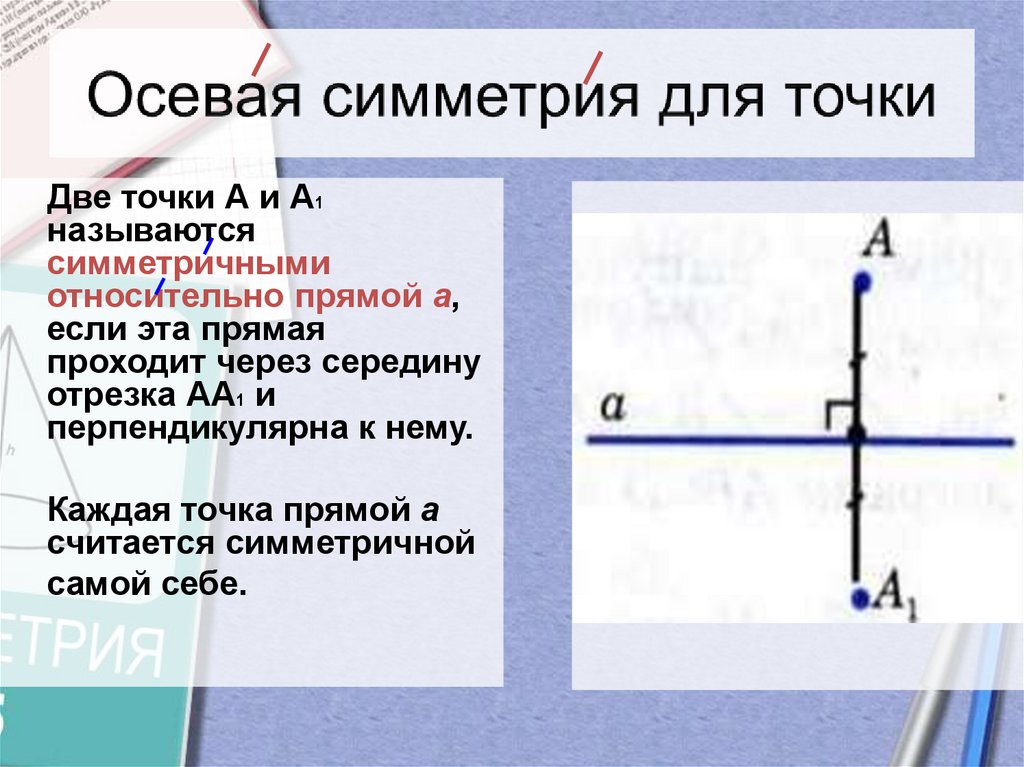
3. Осевая симметрия для точки

Две точки А и А1
называются
симметричными
относительно прямой а,
если эта прямая
проходит через середину
отрезка АА1 и
перпендикулярна к нему.
Каждая точка прямой а
считается симметричной
самой себе.

4. Задание 1

Построить точку
симметричную данной
относительно прямой а

5. Осевая симметрия фигуры

Фигура называется
симметричной
относительно прямой а,
если для каждой точки
симметричная ей точка
относительно прямой а
также принадлежит этой
фигуре.
Прямая а называется осью
симметрии.

6. Задание 2

Определить количество осей
симметрии у фигуры.

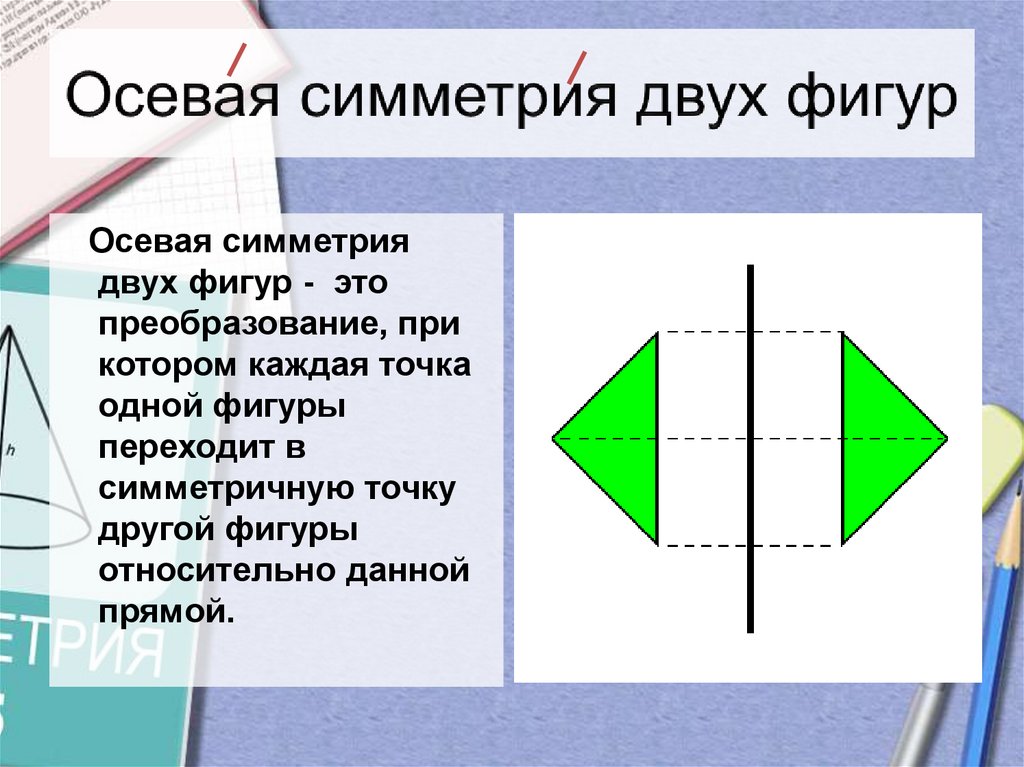
7. Осевая симметрия двух фигур

- это
преобразование, при
котором каждая точка
одной фигуры
переходит в
симметричную точку
другой фигуры
относительно данной
прямой.

8. Задание 3

Построить фигуру
симметричную данной
относительно прямой а

9. Осевая симметрия в природе, технике и архитектуре.

«...быть прекрасным значит
быть симметричным»
Платон

10.

11.

12.

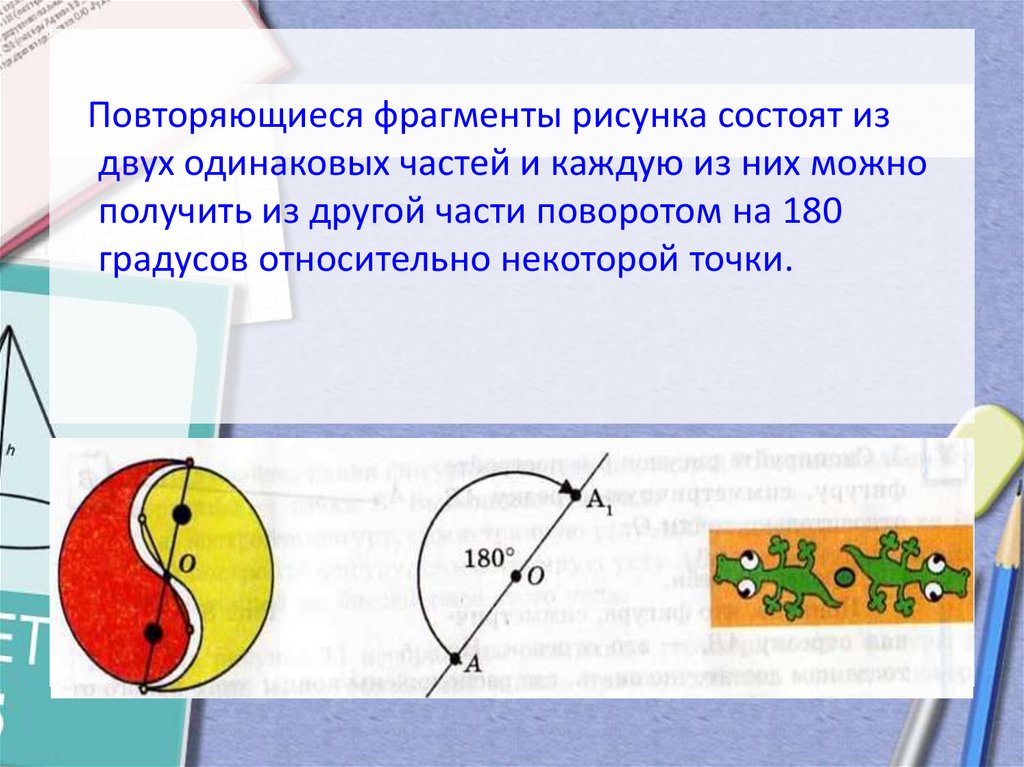
Повторяющиеся фрагменты рисунка состоят из
двух одинаковых частей и каждую из них можно
получить из другой части поворотом на 180
градусов относительно некоторой точки.

13. Центральная симметрия

Две точки А и А1 называются симметричными
относительно точки О, если эта точка – середина
отрезка АА1.
Точка О считается симметричной самой себе.
Фигура называется симметричной относительно точки О, если для
каждой точки фигуры симметричная ей точка относительно точки
О также принадлежит этой фигуре.
Точка О называется центром симметрии.

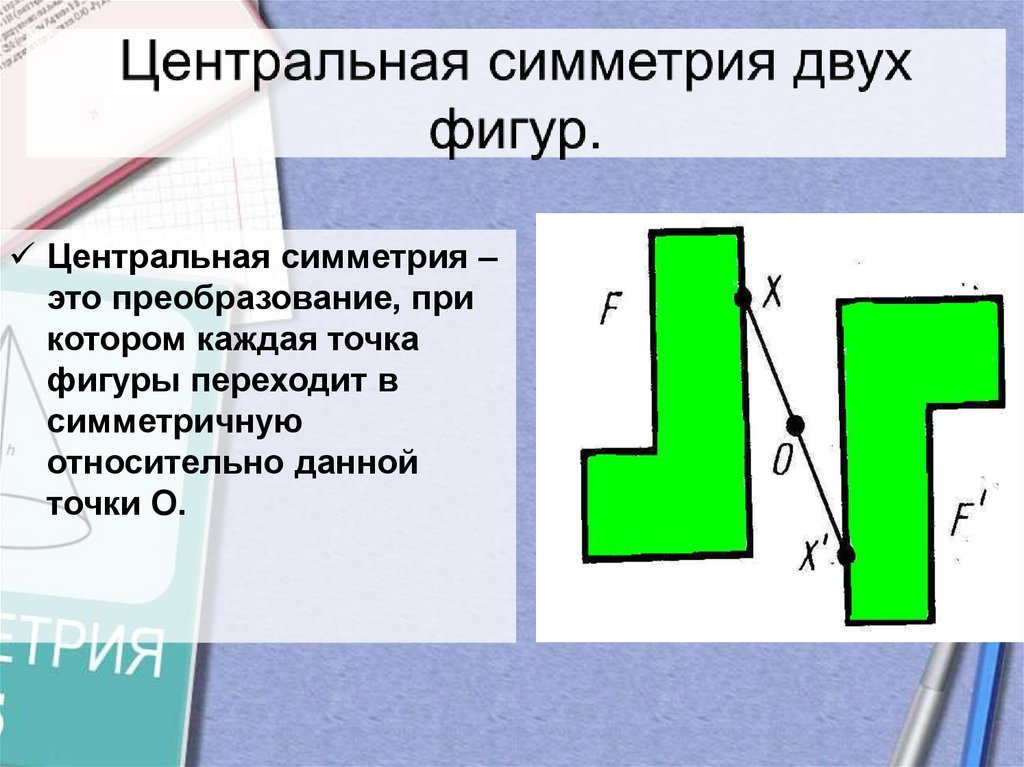
14. Центральная симметрия двух фигур.

Центральная симметрия –
это преобразование, при
котором каждая точка
фигуры переходит в
симметричную
относительно данной
точки О.

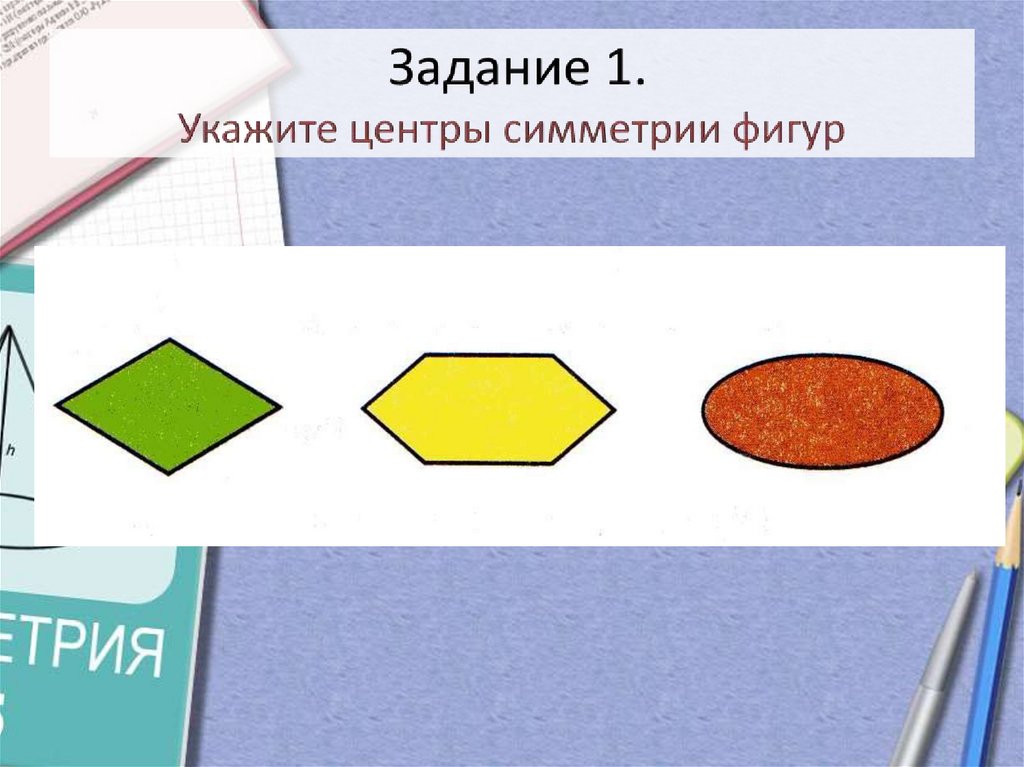
15. Задание 1. Укажите центры симметрии фигур

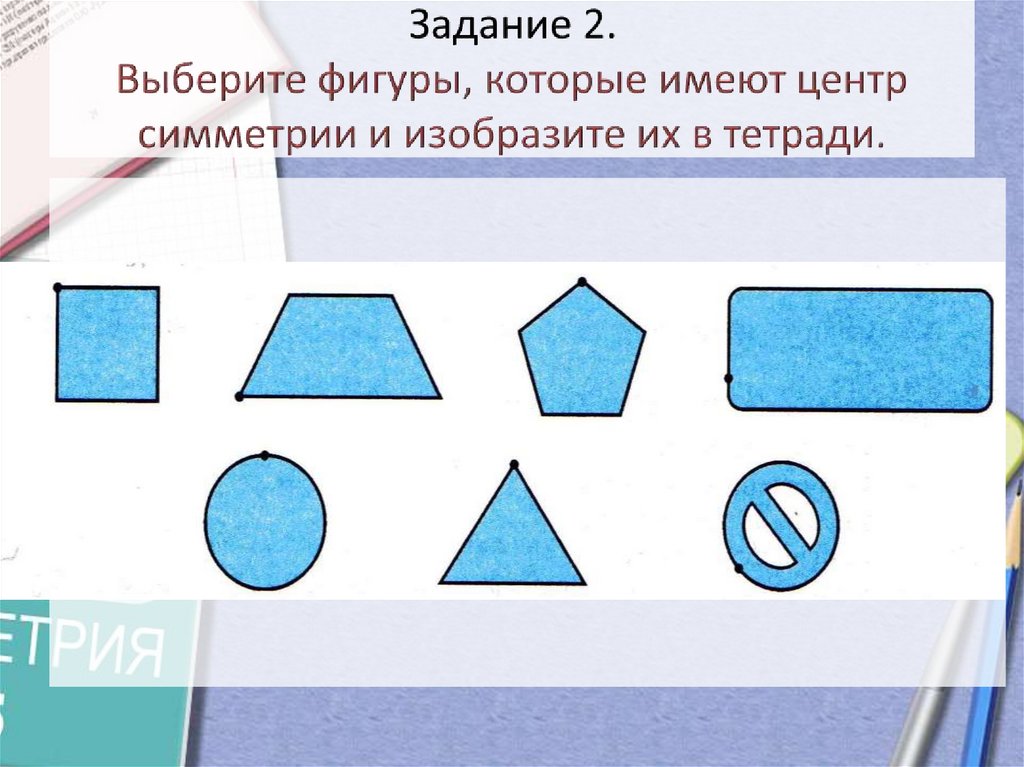
16. Задание 2. Выберите фигуры, которые имеют центр симметрии и изобразите их в тетради.

17. Параллельный перенос

Пусть а – данный вектор
Параллельным переносом на вектор а называется
отображение плоскости, при котором каждая точка М
отображается в такую точку М1, что ММ1=а
Параллельный перенос является движением

18. Поворот

Отметим на плоскости точку О и зададим угол А
Поворотом плоскости вокруг точки О на угол А
называется отображение плоскости, при котором каждая
точка М отображается в точку М1 так, что ОМ = ОМ1 и угол
МОМ1 равен углу А
Поворот является движением