Похожие презентации:
Определение подобных треугольников. Признаки подобия треугольников. 8 класс
1. Тема урока: Определение подобных треугольников. Признаки подобия треугольников
8 класс25 января
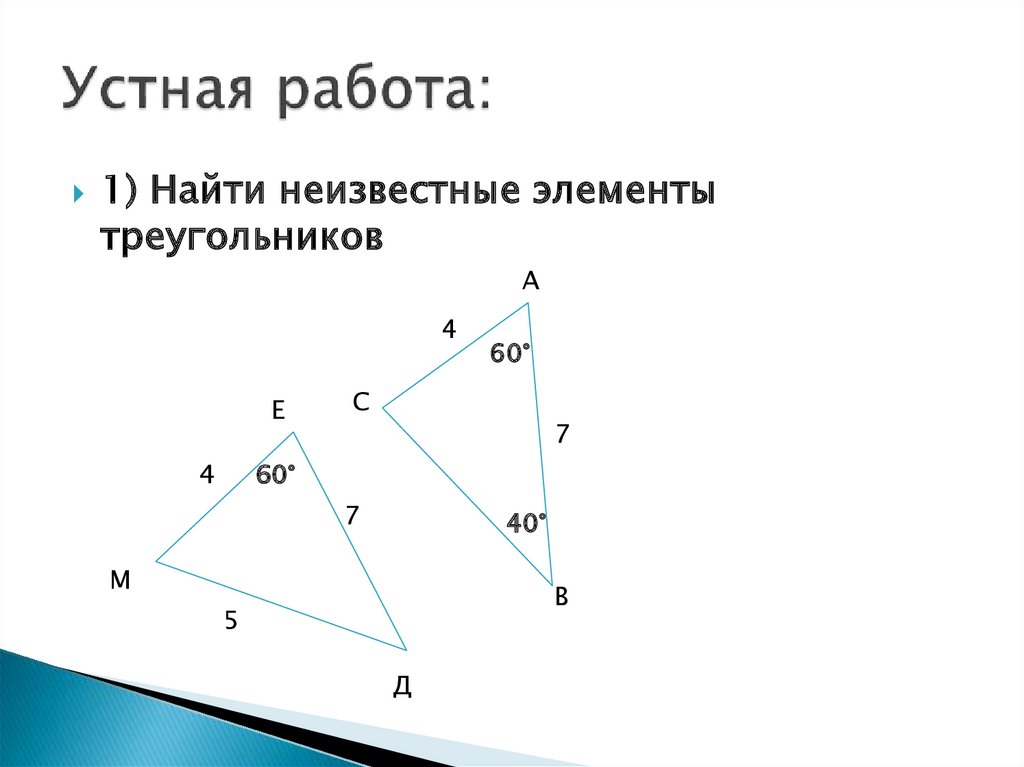
2. Устная работа:
1) Найти неизвестные элементытреугольников
А
4
Е
4
60°
С
7
60°
7
40°
М
В
5
Д
3. 2) Найти неизвестные элементы треугольников
А9
В
20°
50°
12
С
М
7
20°
Е
50°
12
Д
4. Определение :
1)Отношение отрезков АВ и СД называетсяотношением их длин, то есть АВ
СД
2)Отрезки АВ и СД пропорциональны
отрезкам МЕ и КР, если
АВ СД
МЕ
КР
3)Если в треугольниках углы
соответственно равны, то стороны
образующие равные углы называют
сходственными.
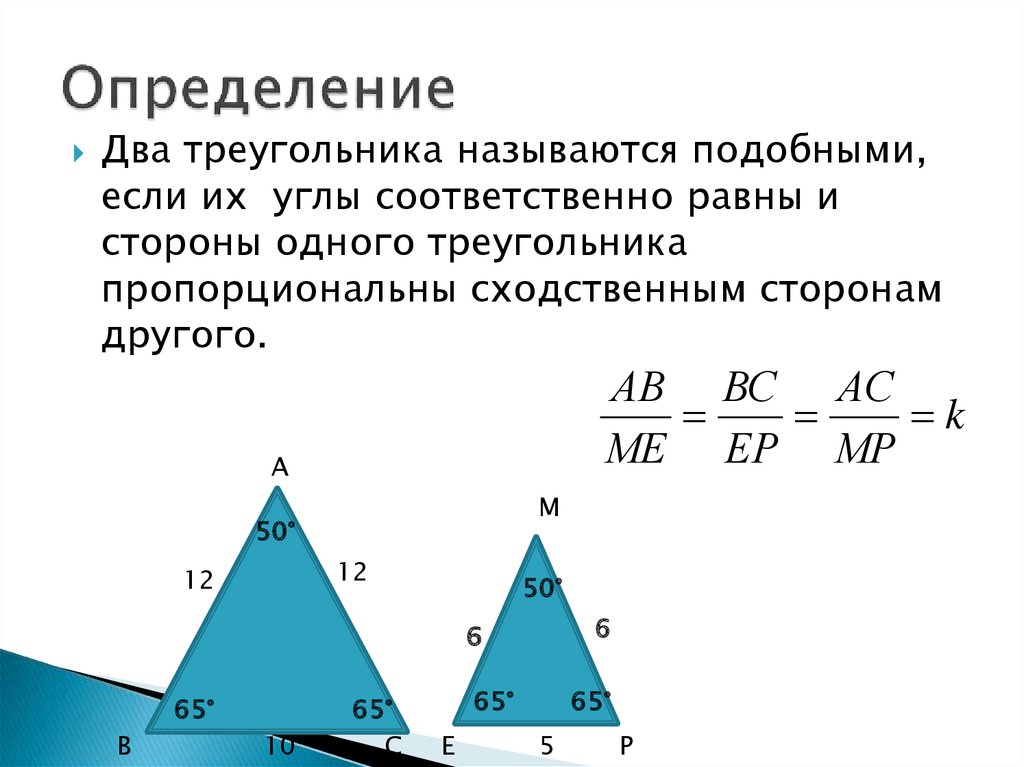
5. Определение
Два треугольника называются подобными,если их углы соответственно равны и
стороны одного треугольника
пропорциональны сходственным сторонам
другого.
АВ ВС АС
k
МЕ ЕР МР
А
М
50°
12
12
50°
6
6
65°
В
10
65°
С
65°
Е
65°
5
Р
6. Отношение площадей подобных треугольников.
Отношение площадей подобныхтреугольников равно квадрату
коэффициента подобия.
S
2
k
S1
7. Первый признак подобия
Если два угла одного треугольникасоответственно равны двум углам другого,
то такие треугольники подобны.
20°
20°
50°
50°
8. Второй признак подобия треугольников
Если две стороны одного треугольникапропорциональны сторонам второго
треугольника , а углы заключенные между
этими сторонами равны, то такие
треугольники подобны.
10
50°
14
50°
7
5
9. Третий признак подобия треугольников
Если три стороны одного треугольникапропорциональны трем сторонам второго
треугольника, то такие треугольники
подобны.
24
24
21
8
8
7
10. Определение:
Средней линией треугольника называетсяотрезок , соединяющий середины двух его
сторон.
Теорема:
Средняя линия треугольника параллельна
стороне против которой она лежит и равна
её половине
С
Е
А
М
7
14
В
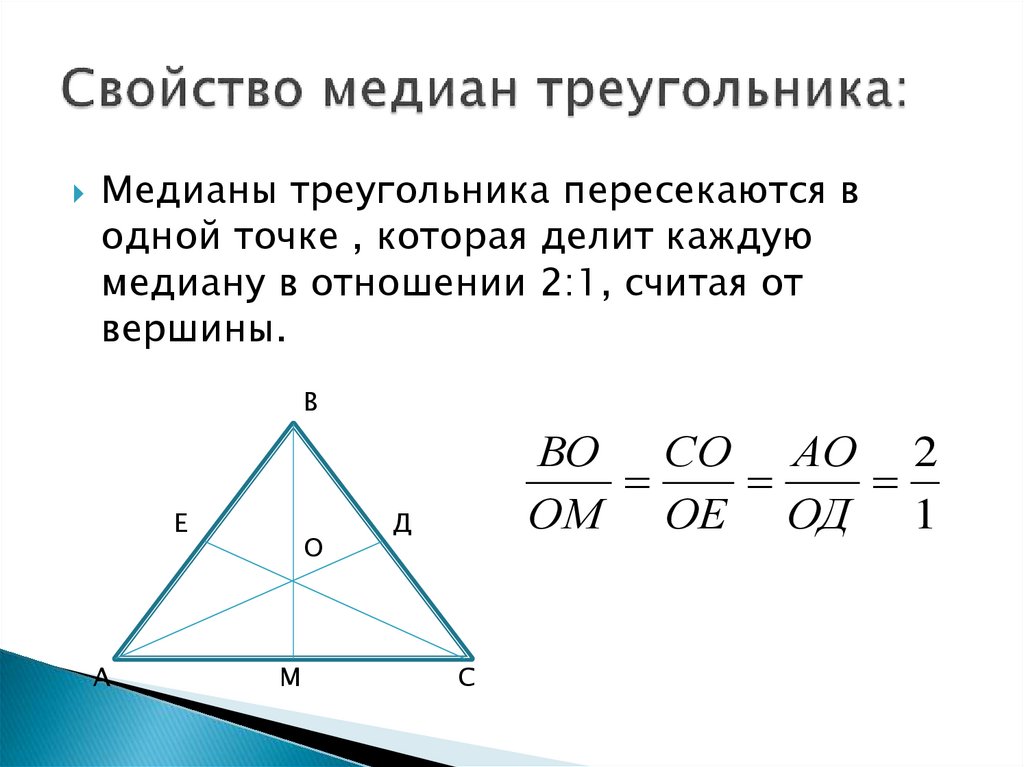
11. Свойство медиан треугольника:
Медианы треугольника пересекаются водной точке , которая делит каждую
медиану в отношении 2:1, считая от
вершины.
В
Е
А
О
М
ВО СО АО 2
ОМ ОЕ ОД 1
Д
С
12. Свойство высоты прямоугольного треугольника
Высота прямоугольного треугольникапроведённая из вершины прямого угла,
есть среднее геометрическое или среднее
пропорциональное для отрезков, на
которые делится гипотенуза.
С
А
Д
СД АД ДВ
В
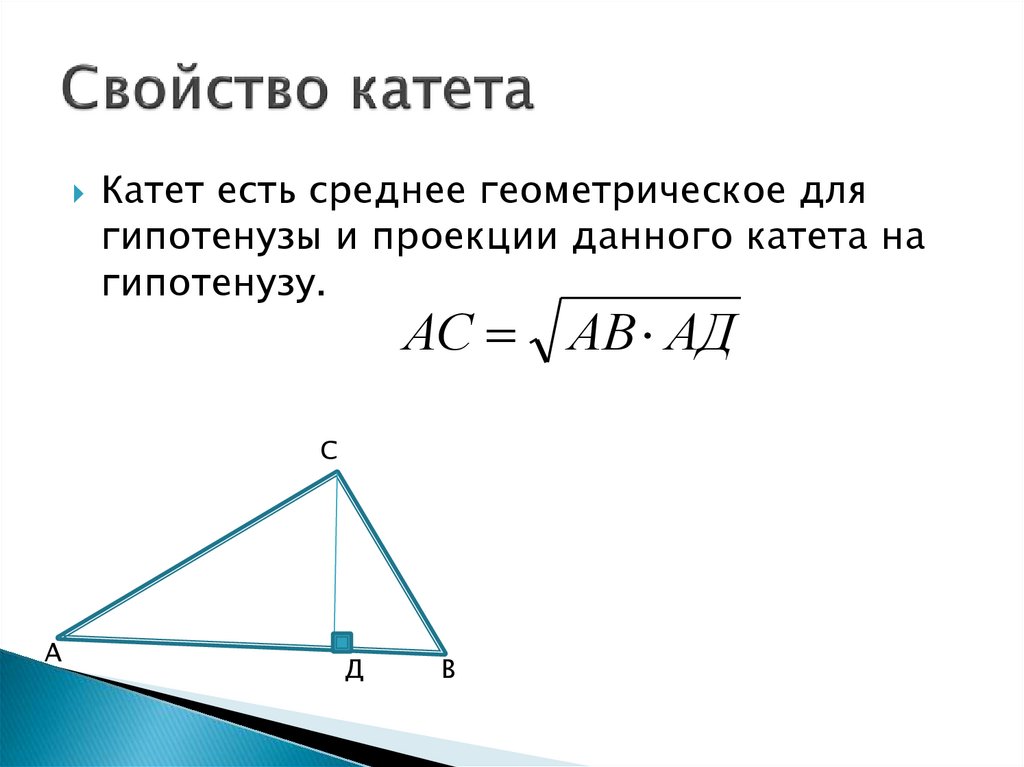
13. Свойство катета
Катет есть среднее геометрическое длягипотенузы и проекции данного катета на
гипотенузу.
АС АВ АД
С
А
Д
В
14. Классная работа:
№564№566
Домашнее задание:
№570
№580










 Математика
Математика








