Тетраэдр

1.

2. Тетраэдр

D
Тетраэдр
• Рассмотрим
произвольный
треугольник АВС и
точку D, не лежащую
в плоскости этого
В треугольника.
А
С

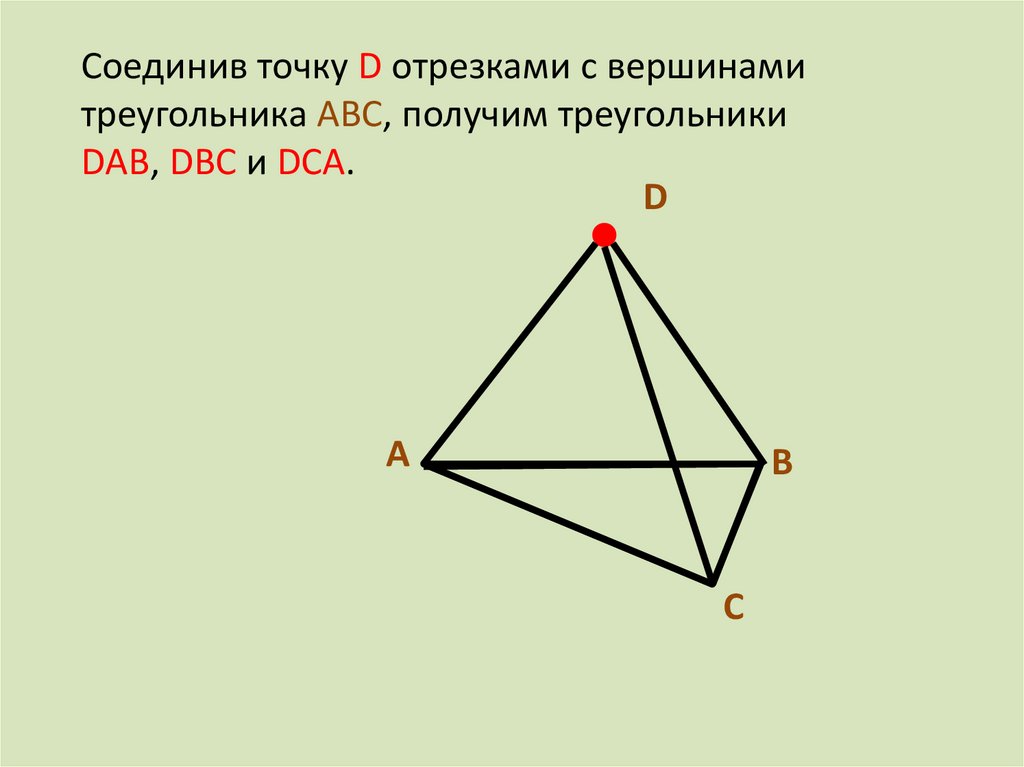
3. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DАВ, DВС и DСА.

D
А
В
С

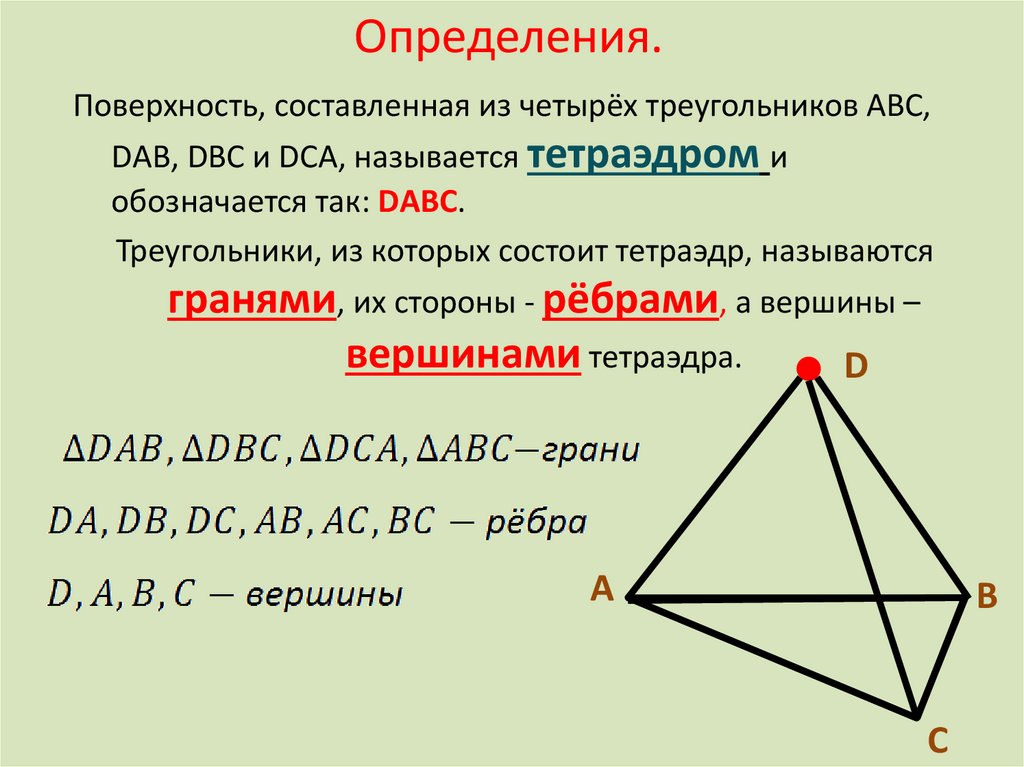
4. Определения.

Поверхность, составленная из четырёх треугольников АВС,
DАВ, DВС и DСА, называется тетраэдром и
обозначается так: DАВС.
Треугольники, из которых состоит тетраэдр, называются
гранями, их стороны - рёбрами, а вершины –
вершинами тетраэдра.
D
А
В
С

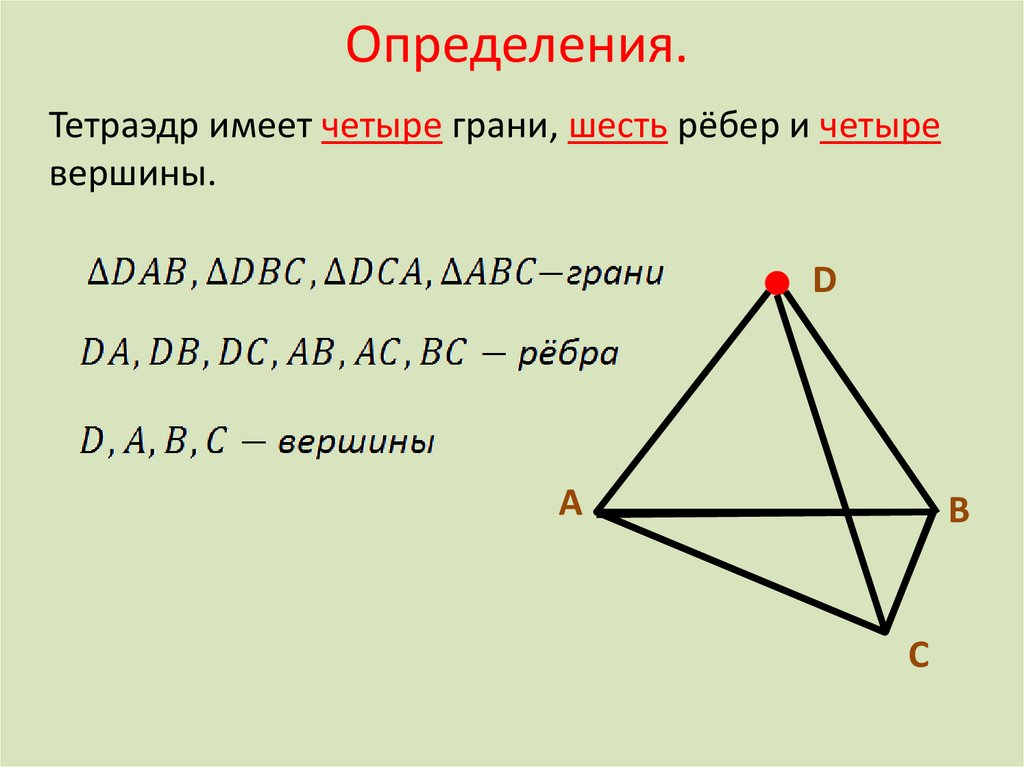
5. Определения.

Тетраэдр имеет четыре грани, шесть рёбер и четыре
вершины.
D
А
В
С

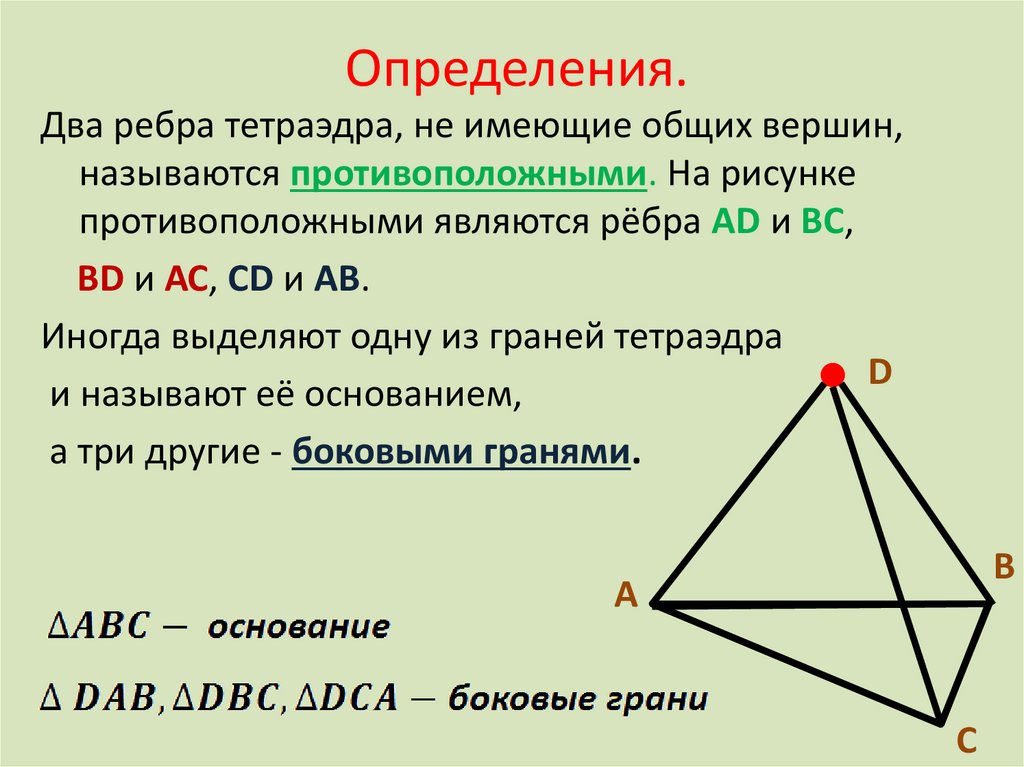
6. Определения.

Два ребра тетраэдра, не имеющие общих вершин,
называются противоположными. На рисунке
противоположными являются рёбра АD и ВС,
ВD и АС, СD и АВ.
Иногда выделяют одну из граней тетраэдра
D
и называют её основанием,
а три другие - боковыми гранями.
В
А
С

7.

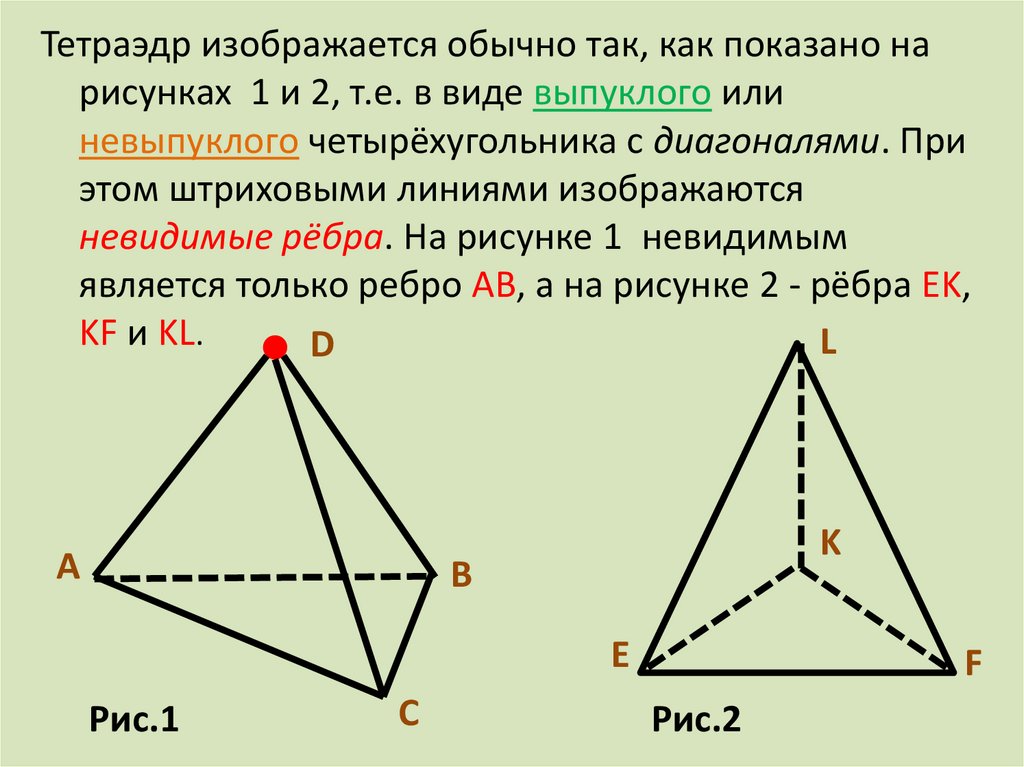
Тетраэдр изображается обычно так, как показано на
рисунках 1 и 2, т.е. в виде выпуклого или
невыпуклого четырёхугольника с диагоналями. При
этом штриховыми линиями изображаются
невидимые рёбра. На рисунке 1 невидимым
является только ребро АB, а на рисунке 2 - рёбра EK,
KF и KL.
L
D
А
K
В
E
Рис.1
С
F
Рис.2

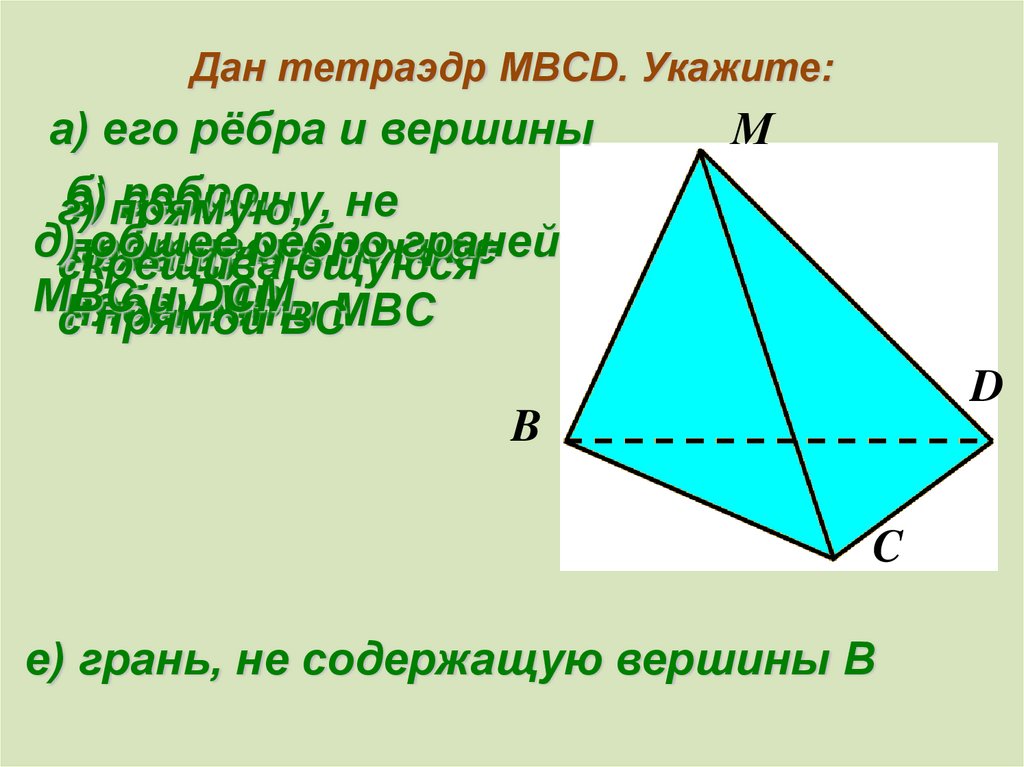
8. Дан тетраэдр MBCD. Укажите:

а) его рёбра и вершины
б)
ребро,
в) прямую,
вершину,
не
г)
д)скрещивающуюся
общее ребро
граней
противоположное
лежащую
в
MBC
и
DCM
ребру
MBBCMBC
плоскости
с прямой
М
D
B
C
е) грань, не содержащую вершины В