Похожие презентации:
Описанная окружность
1. Описанная окружность
2. Опрос
Какая окружность называется вписаннойв многоугольник?
Какой многоугольник называется
описанным возле окружности?
В любой ли треугольник можно вписать
окружность?
Сколько окружностей можно вписать в
треугольник?
Где лежит центр вписанной окружности?
3. Опрос
Чему равен радиус окружности,вписанной в треугольник?
В любой ли четырехугольник можно
вписать окружность?
Сформулируйте свойство описанного
четырехугольника
Сформулируйте признак описанного
четырехугольника
4. ТЕСТ- ПРОВЕРКА
12
3
4
1 ВАРИАНТ
Б
А
В
А
2 ВАРИАНТ
А
Б
А
В
5. Определение
Если все вершины многоугольникалежат на окружности, то окружность
называется описанной около
многоугольника, многоугольник
вписанным в эту окружность.
ABCDE вписан в окружность.
ABFE не вписан в окружность, так
как F не лежит на окружности.
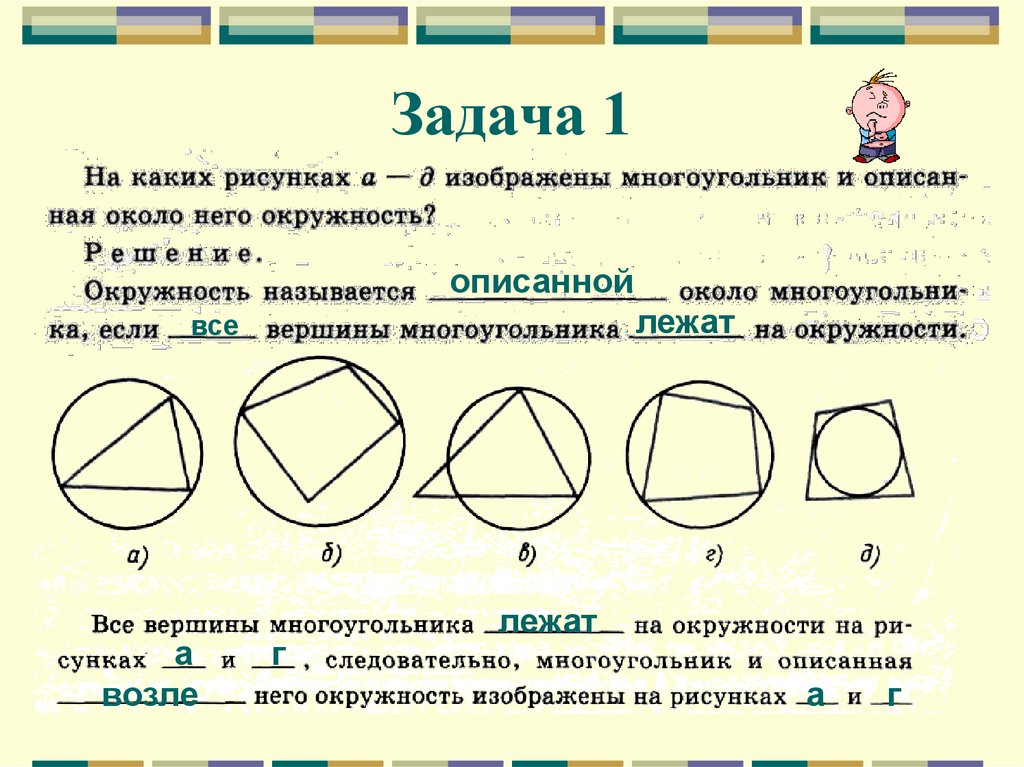
6. Задача 1
описаннойлежат
все
а
возле
г
лежат
а
г
7. Теорема
Около любоготреугольника можно
описать окружность.
Замечание: около треугольника
можно описать только одну
окружность.
8. Дано
ABCMM1 , NN1, KK1
Дано
С
серединные перпендикуляры.
MM1 NN1 KK1 O
M
о
Доказать, что окр.( O;R) –
описанная возле ABC
А
K
N
В
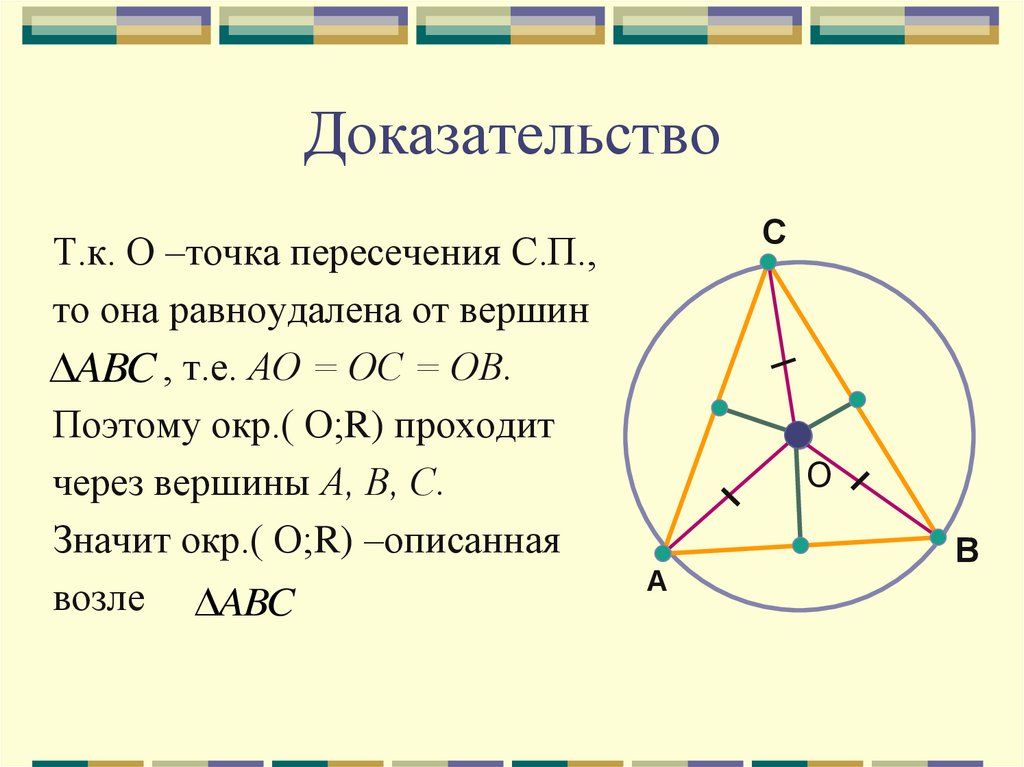
9. Доказательство
Т.к. О –точка пересечения С.П.,то она равноудалена от вершин
ABC , т.е. АО = ОС = ОВ.
Поэтому окр.( О;R) проходит
через вершины А, В, С.
Значит окр.( О;R) –описанная
возле ABC
С
О
А
В
10. Важный вывод 1
Центр, описанной возлетреугольника окружности,
лежит в точке пересечения его
серединных перпендикуляров
и равноудален от его вершин.
11. Важный вывод 2
Радиус окружности, описаннойвозле треугольника,
равен расстоянию от центра
окружности до вершин
треугольника.
12. Около четырехугольника не всегда можно описать окружность.
Если возле четырехугольникаможно описать окружность, то
его стороны обладают
следующим свойством:
13. Свойство
В любом вписанномчетырехугольнике сумма
противоположных углов
равна 180°
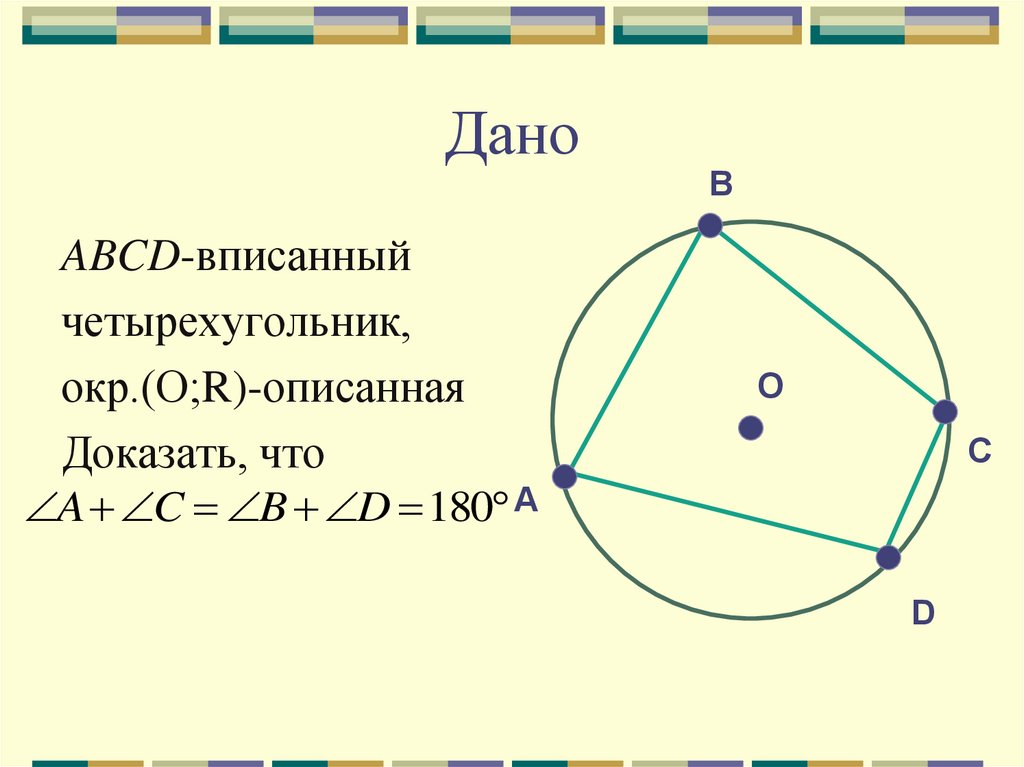
14. Дано
ABCD-вписанныйчетырехугольник,
окр.(О;R)-описанная
Доказать, что
A C B D 180 А
В
O
С
D
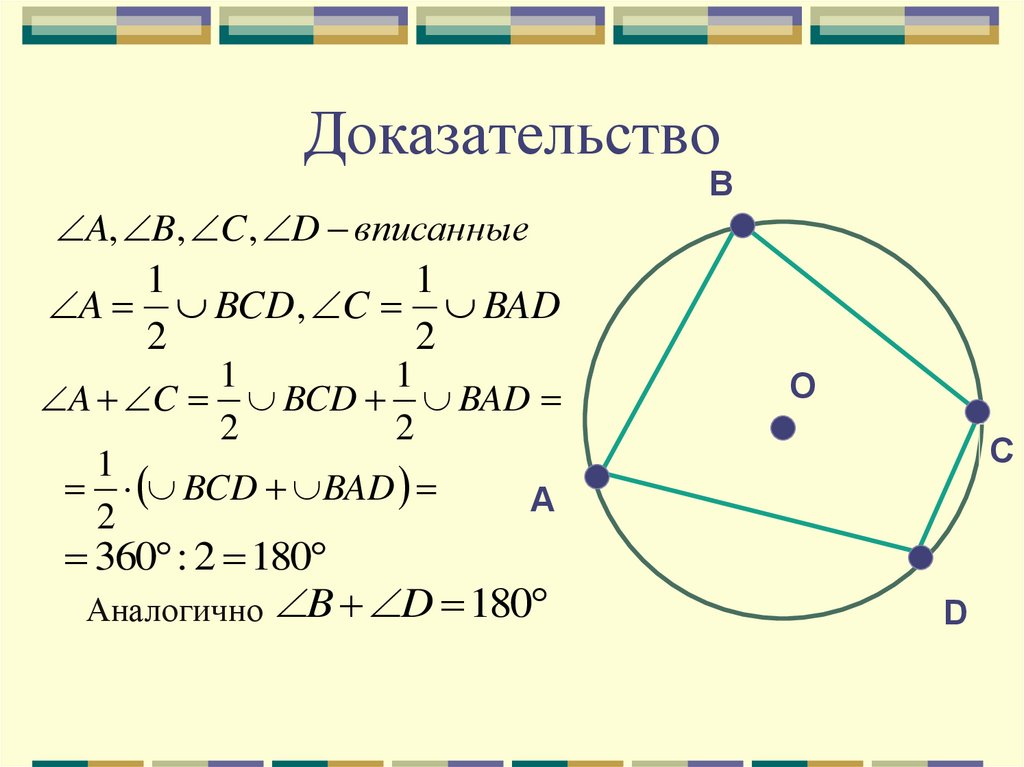
15. Доказательство
A, B, C , D вписанные1
1
A BCD , C BAD
2
2
1
1
A C BCD BAD
2
2
1
BCD BAD
А
2
360 : 2 180
Аналогично B D 180
В
O
С
D
16. Верно и обратное утверждение
Если сумма противолежащихуглов четырехугольника
равна 180°, то около него можно
описать окружность.
Это признак вписанного
четырехугольника
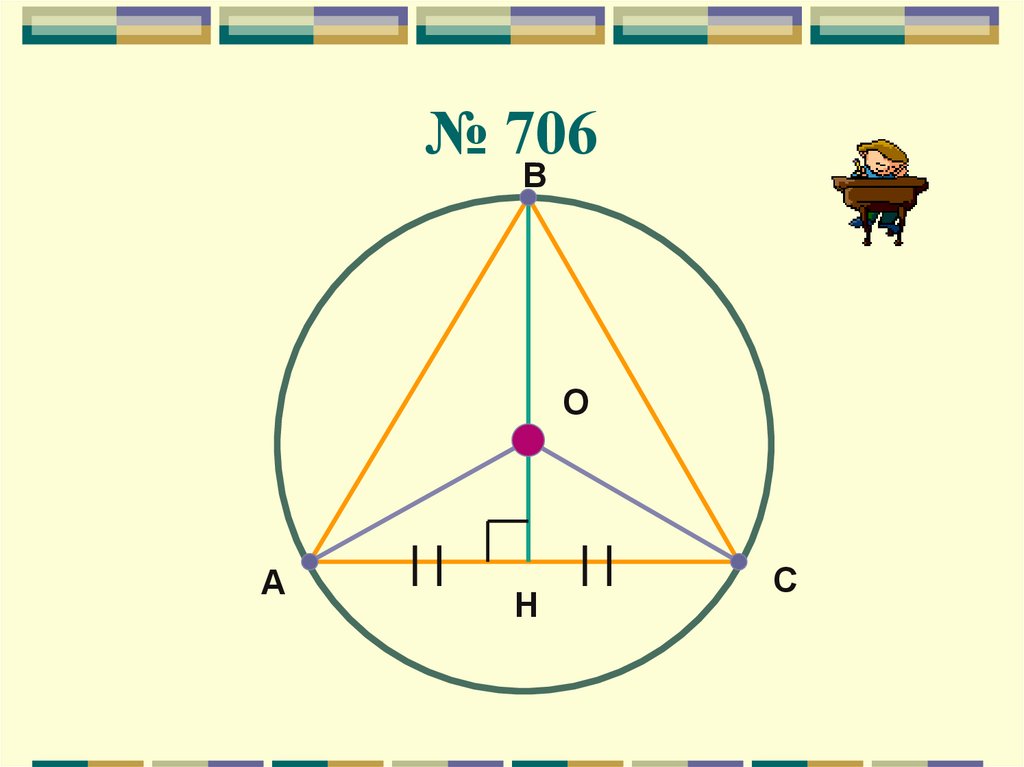
17. № 706
ВО
А
H
С
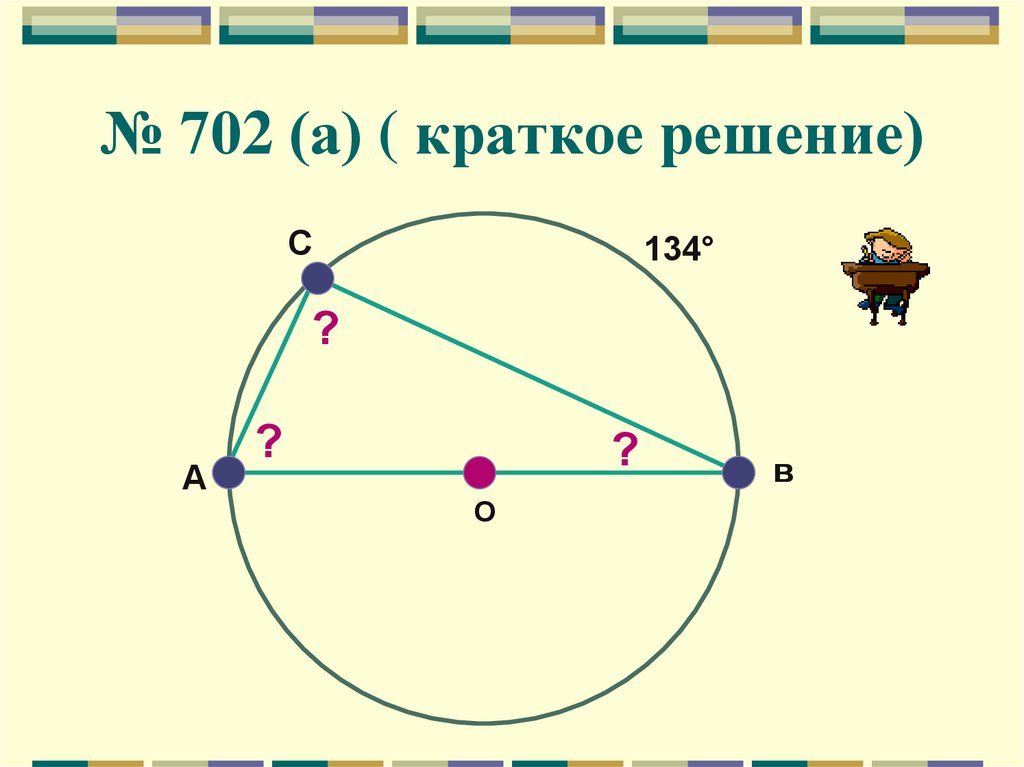
18. № 702 (а) ( краткое решение)
C134°
?
A
?
?
O
в
19. № 703
AA
?
B
?
?
?
O
O
?
B
?
C
C
20. № 705 а ( краткое решение)
C8
6
В
A
O
21. Подведем итог :
Какая окружность называется описанной?Какой многоугольник называется вписанным?
Возле любого треугольника можно описать
окружность?
Сколько окружностей можно описать возле
треугольника?
Где лежит центр описанной окружности?
22. Подведем итоги :
Чему равен радиус окружности,описанной возле треугольника?
Возле любого ли четырехугольника
можно описать окружность?
Сформулируйте свойство вписанного
четырехугольника
Сформулируйте признак описанного
четырехугольника
23. Домашние задание
П.74. читатьТеория из тетрадки, формулировки знать
наизусть.
№ 702 (Б), 705 (Б), 707

















 Математика
Математика








