Решение задач по теме «Площадь параллелограмма, треугольника, трапеции»

1. Решение задач по теме «Площадь параллелограмма, треугольника, трапеции»

Шаляпина Галина Ивановна учитель математики
МБОУ «Нижнекулойская средняя
общеобразовательная школа» Верховажского
района Вологодской области

2.

Вычисление площадей
фигур на клетчатой
бумаге
1
2
3
4
5
6
7
8
9
10
11
12

3.

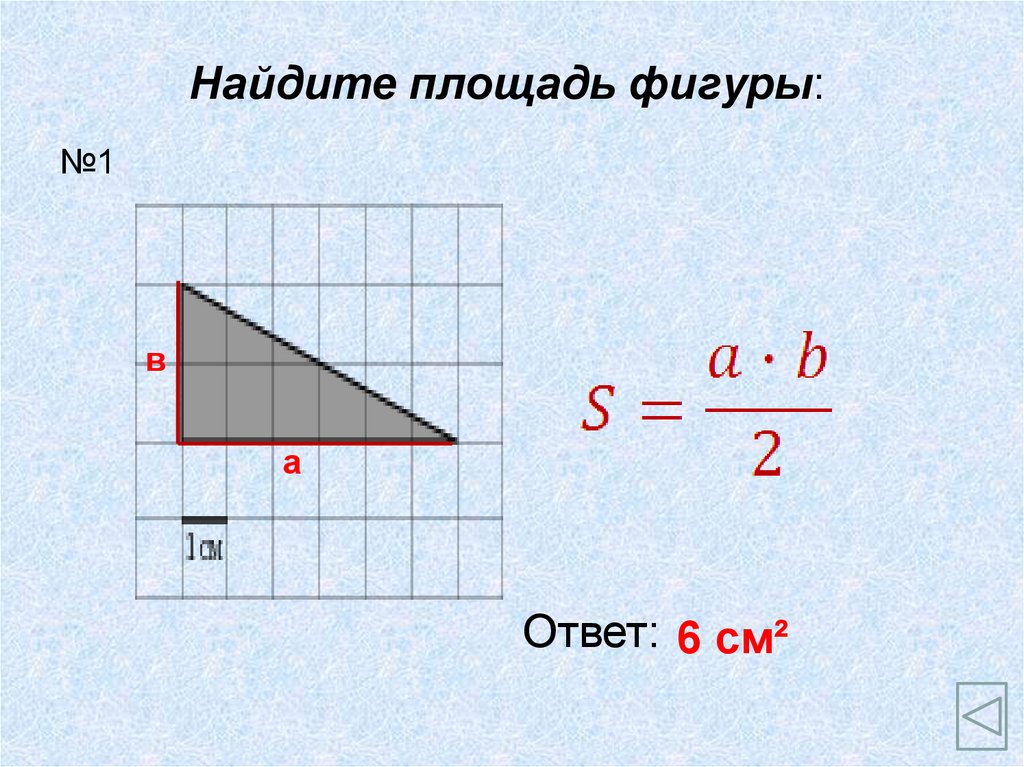
Найдите площадь фигуры:
№1
в
а
Ответ: 6 см²

4.

Найдите площадь фигуры:
№2
h
а
Ответ: 6 см²

5.

Найдите площадь фигуры:
№3
a
h
Ответ: 12 см²

6.

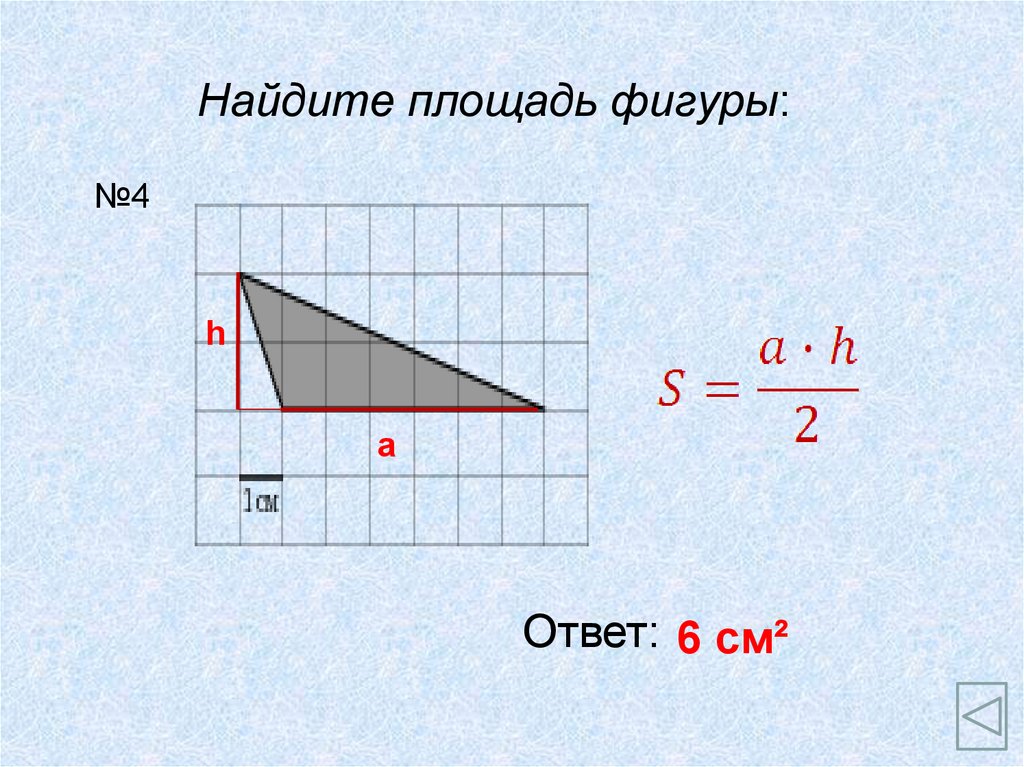
Найдите площадь фигуры:
№4
h
a
Ответ: 6 см²

7.

Найдите площадь фигуры:
№5
Ответ: 28 см²

8.

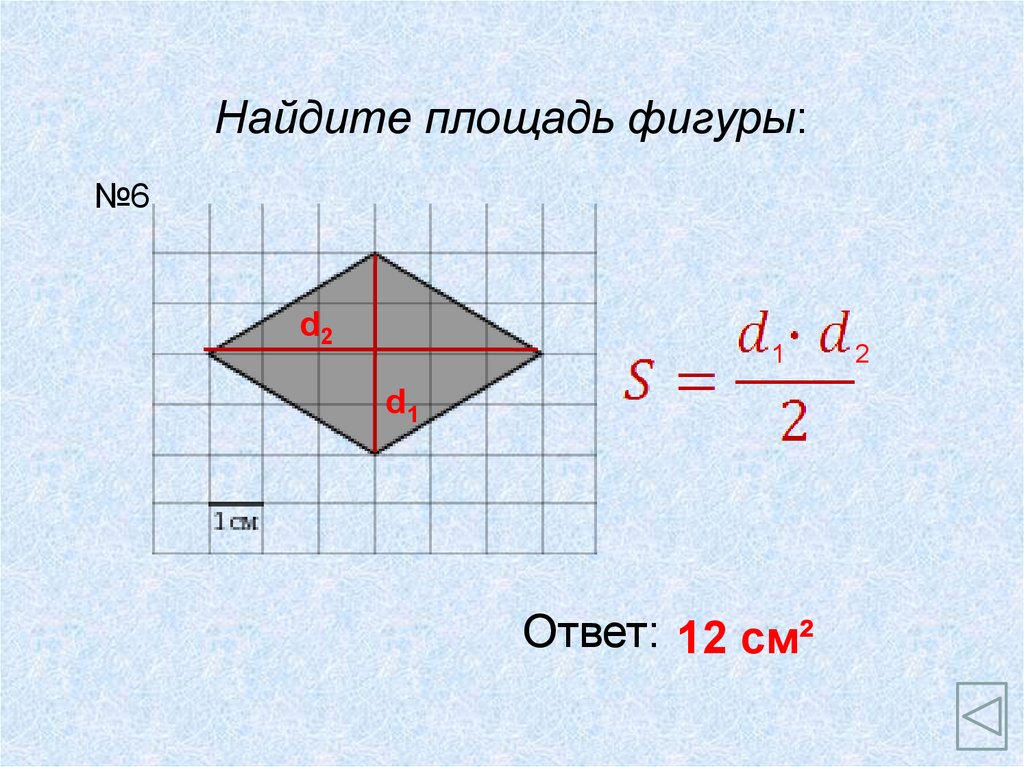
Найдите площадь фигуры:
№6
d2
1
d1
Ответ: 12 см²
2

9.

Найдите площадь фигуры:
№7
a
h
S=
b
Ответ: 17,5 см²

10.

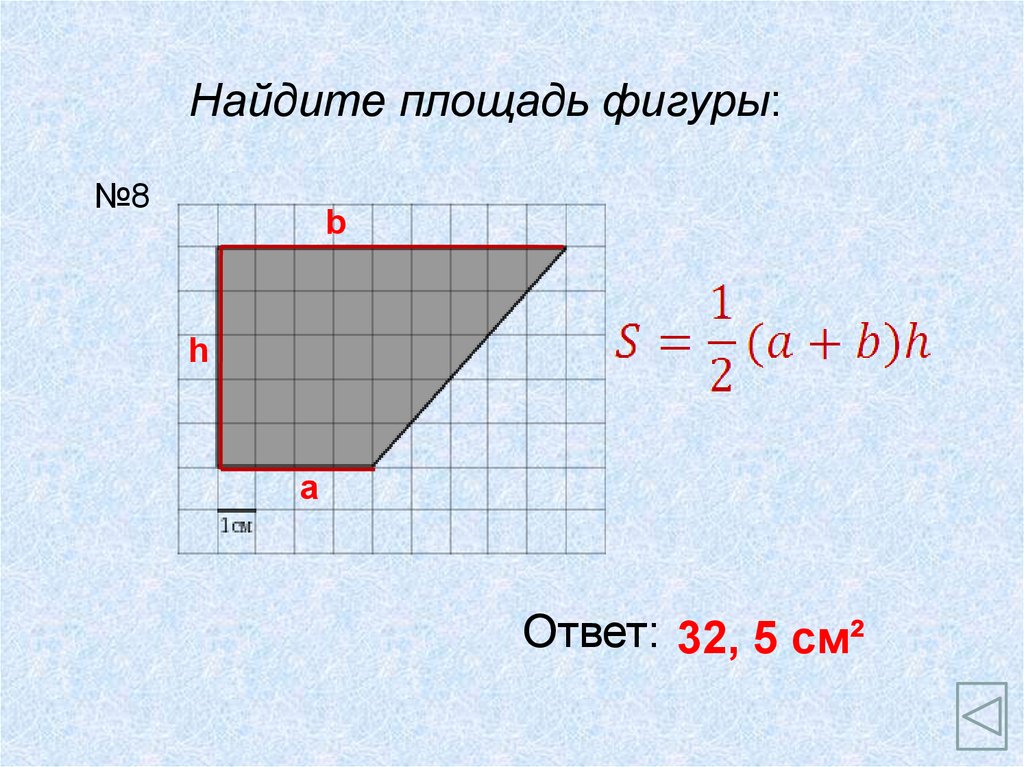
Найдите площадь фигуры:
№8
b
h
a
Ответ: 32, 5 см²

11.

Найдите площадь фигуры:
№9
h
b
a
Ответ: 15 см²

12.

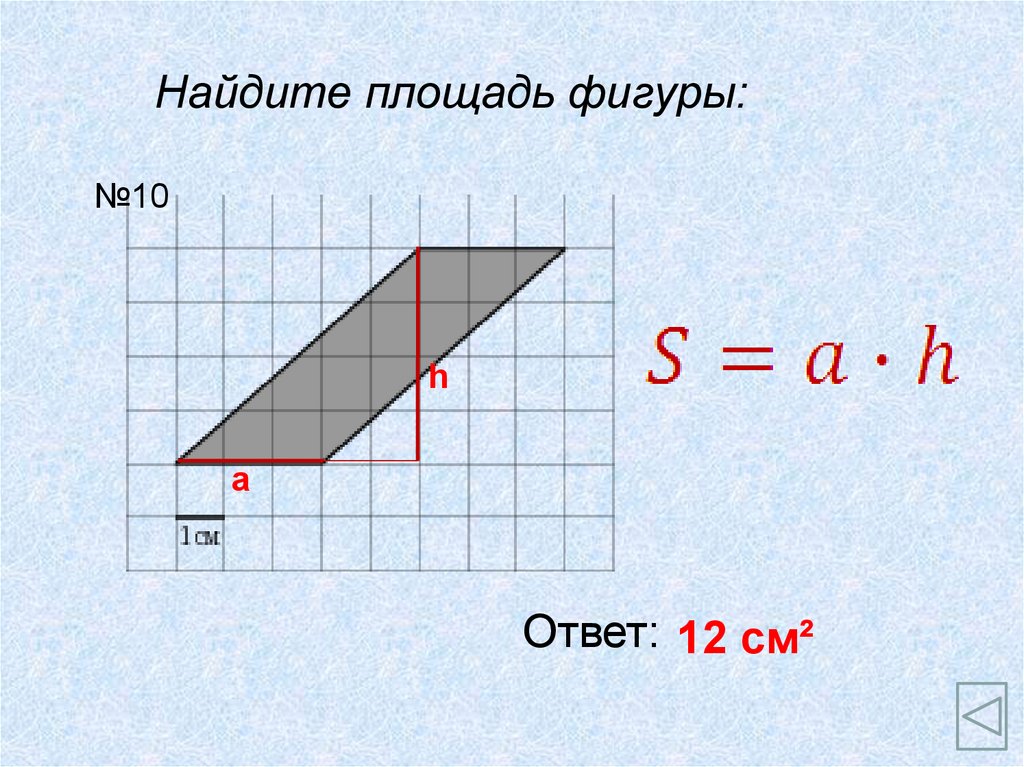
Найдите площадь фигуры:
№10
h
a
Ответ: 12 см²

13.

Найдите площадь фигуры:
№11
Ответ: 6 см²

14.

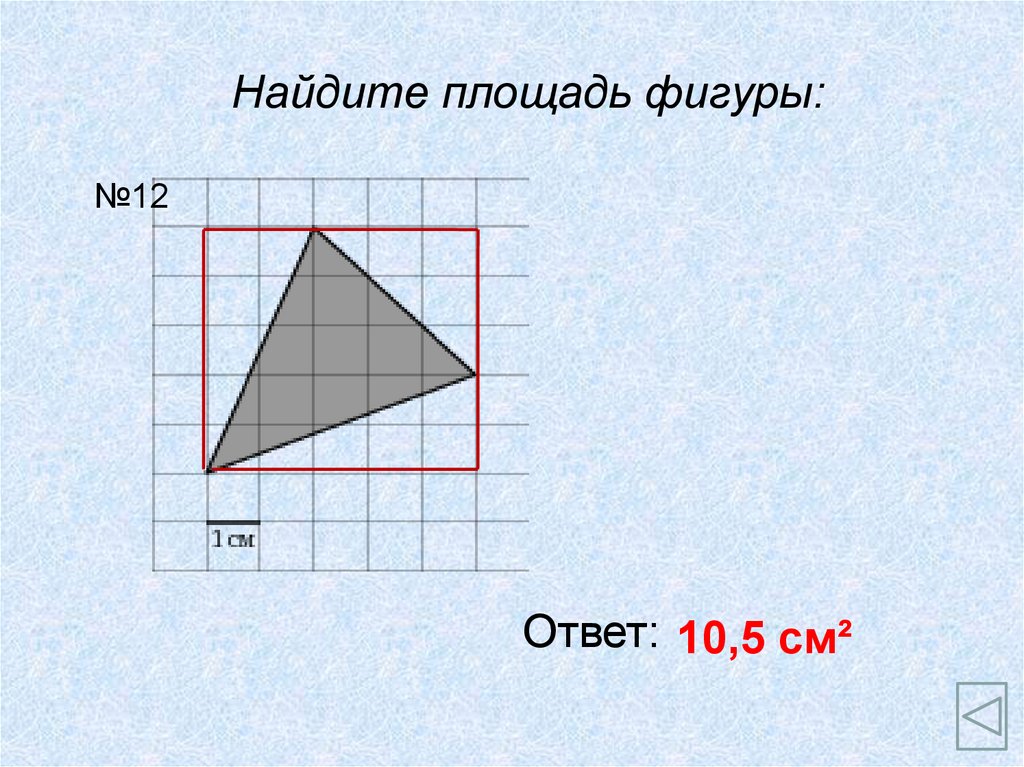
Найдите площадь фигуры:
№12
Ответ: 10,5 см²

15.

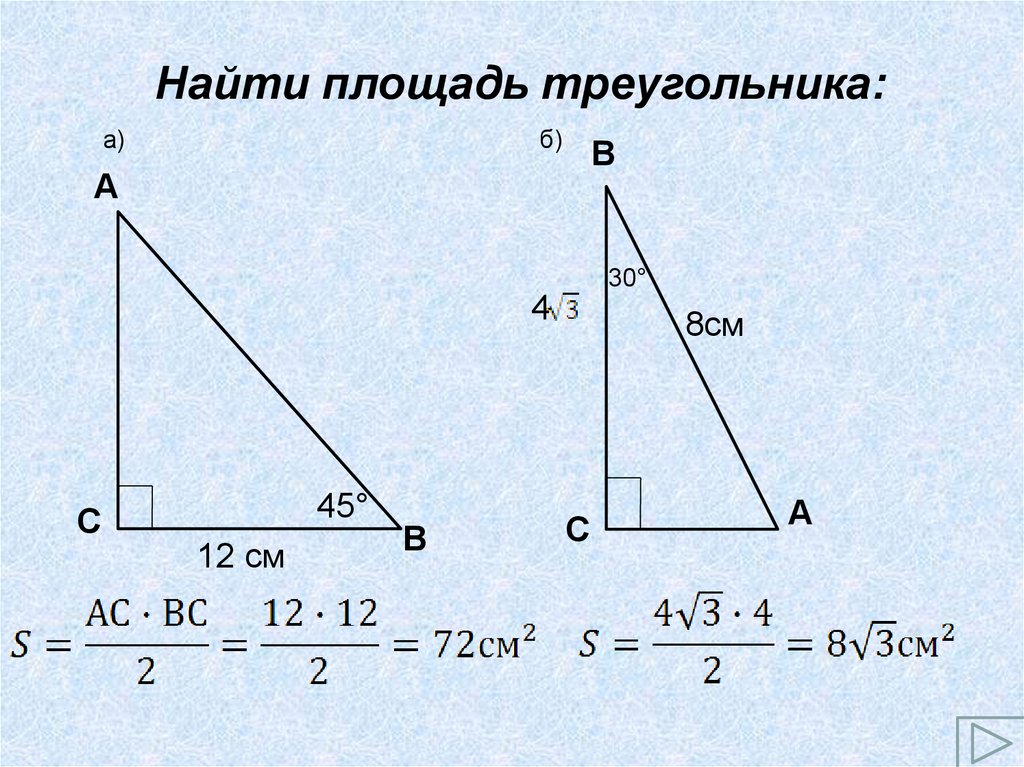
Найти площадь треугольника:
а)
б)
В
А
30°
4
С
45°
12 см
В
8см
С
А

16.

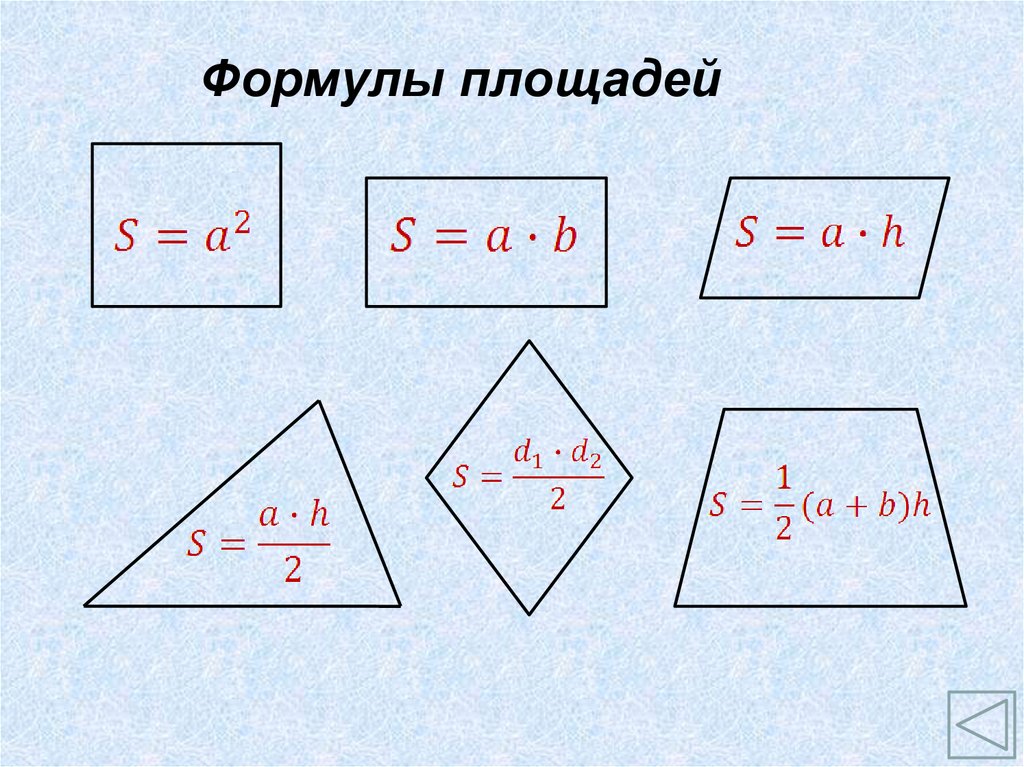
Формулы площадей

17.

Задачи урока:
•закрепить навыки вычисления
площади фигур по формуле
•научиться применять
изученные свойства фигур для
решения задач на вычисление
площади

18.

1. В треугольнике АВС С = 135 ,
АС = 6 дм, высота ВД равна 2 дм. Найти
площадь треугольника АВД.
В
Решение:
АВД- прямоугольный
А
С
Д
ВСД – прямоугольный, ВСД = 180 -135 = 45
СВД =45 ВСД- равнобедренный, СД = ВД =
=2 дм АД = АС + СД = 8 дм
Ответ: 8дм²

19.

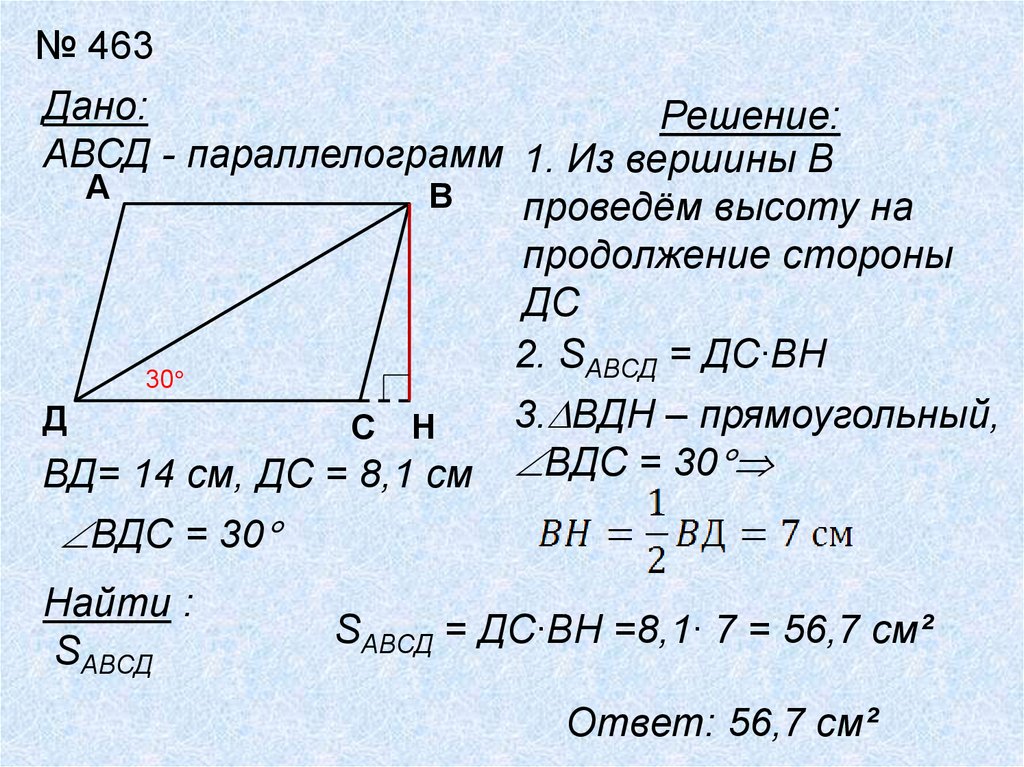
№ 463
Дано:
Решение:
АВСД - параллелограмм 1. Из вершины В
А
В
проведём высоту на
продолжение стороны
ДС
2. SАВСД = ДС∙ВН
30
Д
С
Н
ВД= 14 см, ДС = 8,1 см
3. ВДН – прямоугольный,
ВДС = 30
ВДС = 30
Найти :
SАВСД
SАВСД = ДС∙ВН =8,1∙ 7 = 56,7 см²
Ответ: 56,7 см²

20.

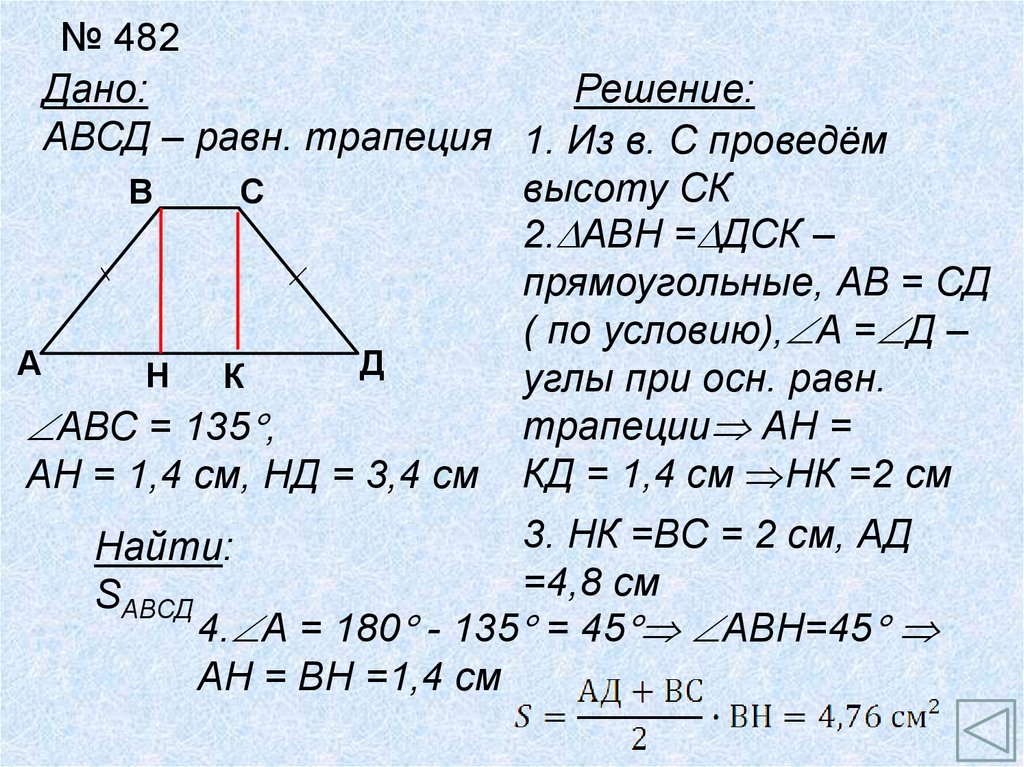
№ 482
Дано:
Решение:
АВСД – равн. трапеция 1. Из в. С проведём
высоту СК
В
С
2. АВН = ДСК –
прямоугольные, АВ = СД
( по условию), А = Д –
А
Д
Н
К
углы при осн. равн.
трапеции АН =
АВС = 135 ,
АН = 1,4 см, НД = 3,4 см КД = 1,4 см НК =2 см
3. НК =ВС = 2 см, АД
Найти:
=4,8 см
SАВСД
4. А = 180 - 135 = 45 АВН=45
АН = ВН =1,4 см