Похожие презентации:
Правильные многоугольники
1.
Правильныемногоугольники
2. Выпуклый многоугольник
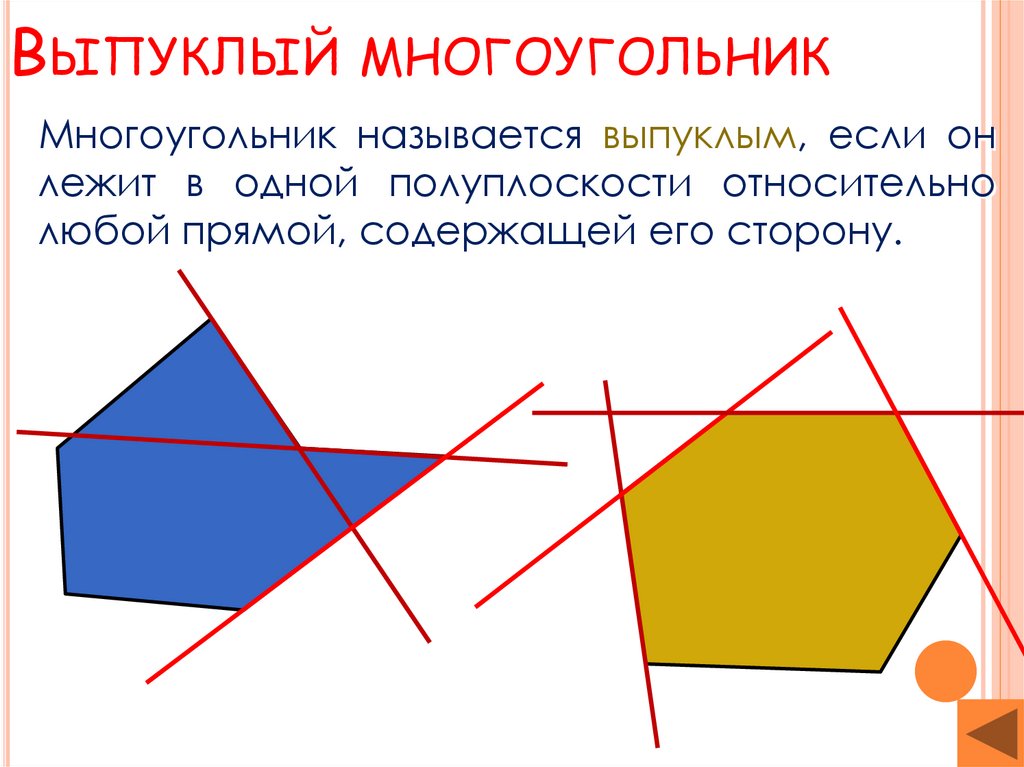
ВЫПУКЛЫЙМНОГОУГОЛЬНИК
Многоугольник называется выпуклым, если он
лежит в одной полуплоскости относительно
любой прямой, содержащей его сторону.
3. Сумма углов выпуклого n – угольника
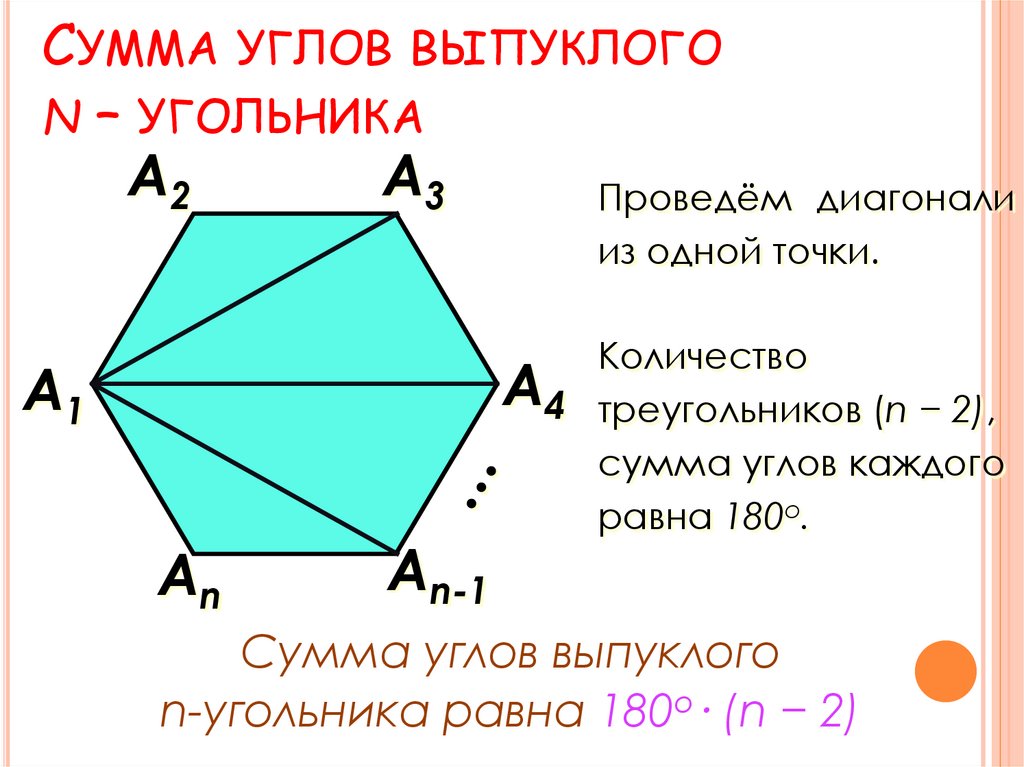
СУММА УГЛОВ ВЫПУКЛОГОN – УГОЛЬНИКА
А2
А3
Проведём
диагонали
из одной точки.
А1
Аn
Аn-1
Количество
А4 треугольников (n − 2),
сумма углов каждого
равна 180о.
Сумма углов выпуклого
n-угольника равна 180о· (n − 2)
4. Правильный многоугольник
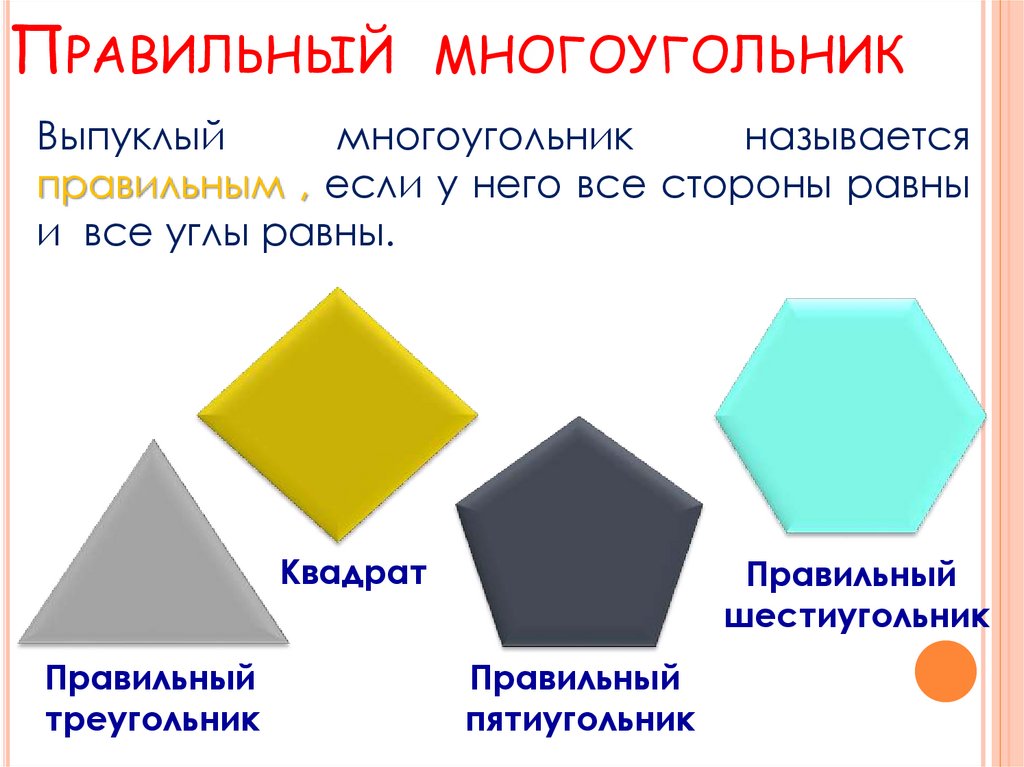
ПРАВИЛЬНЫЙМНОГОУГОЛЬНИК
Выпуклый
многоугольник
называется
правильным , если у него все стороны равны
и все углы равны.
Квадрат
Правильный
треугольник
Правильный
шестиугольник
Правильный
пятиугольник
5.
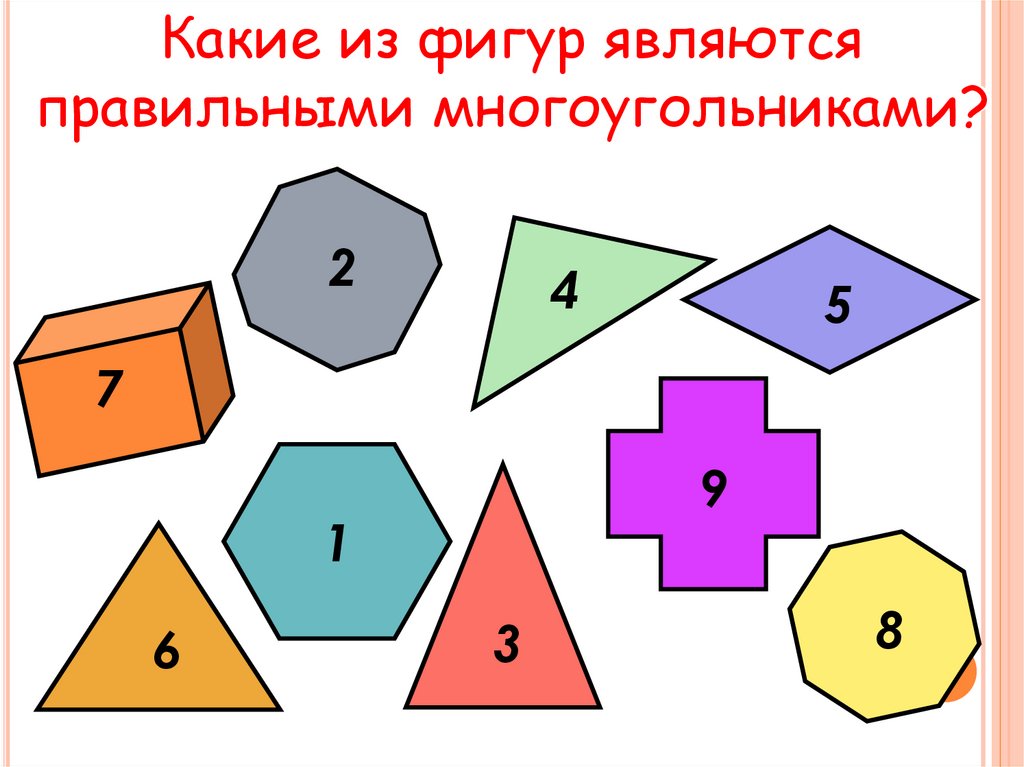
Какие из фигур являютсяправильными многоугольниками?
2
4
5
7
9
1
6
3
8
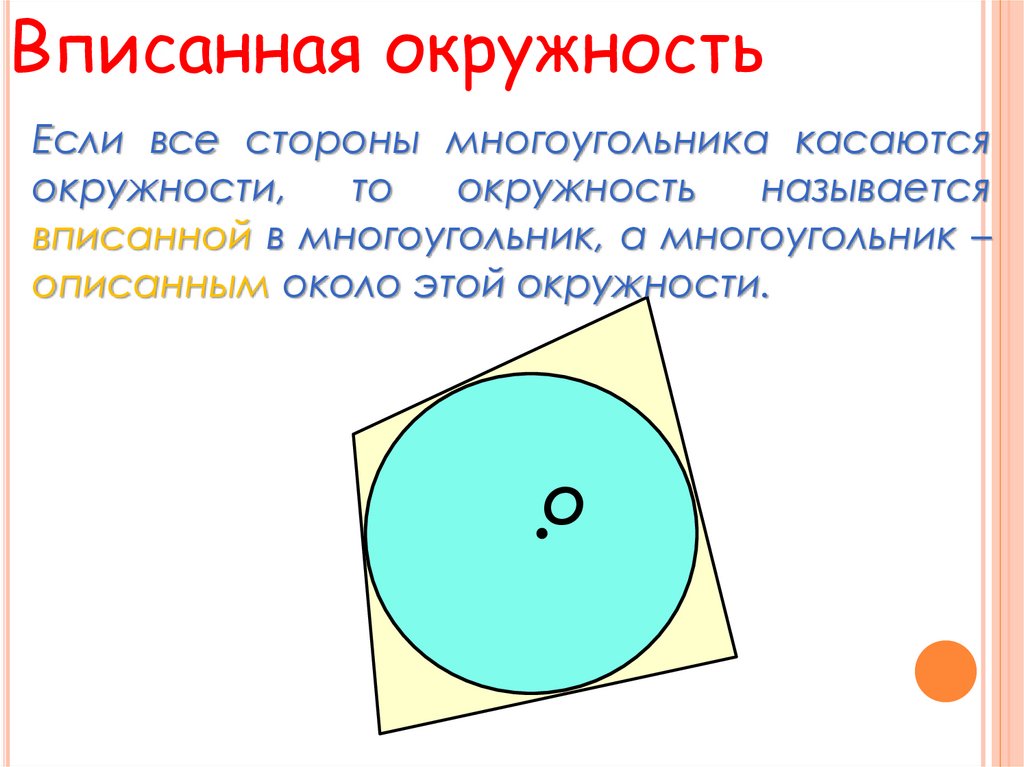
6. Вписанная окружность
Если все стороны многоугольника касаютсяокружности,
то
окружность
называется
вписанной в многоугольник, а многоугольник –
описанным около этой окружности.
О
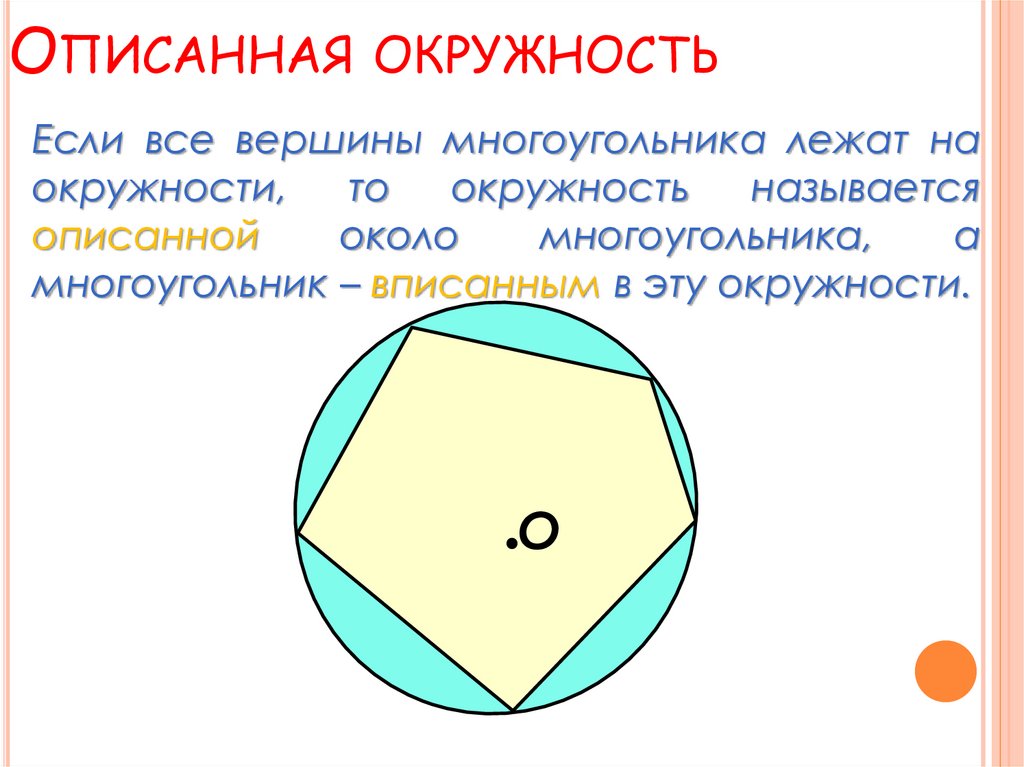
7. Описанная окружность
ОПИСАННАЯОКРУЖНОСТЬ
Если все вершины многоугольника лежат на
окружности,
то
окружность
называется
описанной
около
многоугольника,
а
многоугольник – вписанным в эту окружности.
О
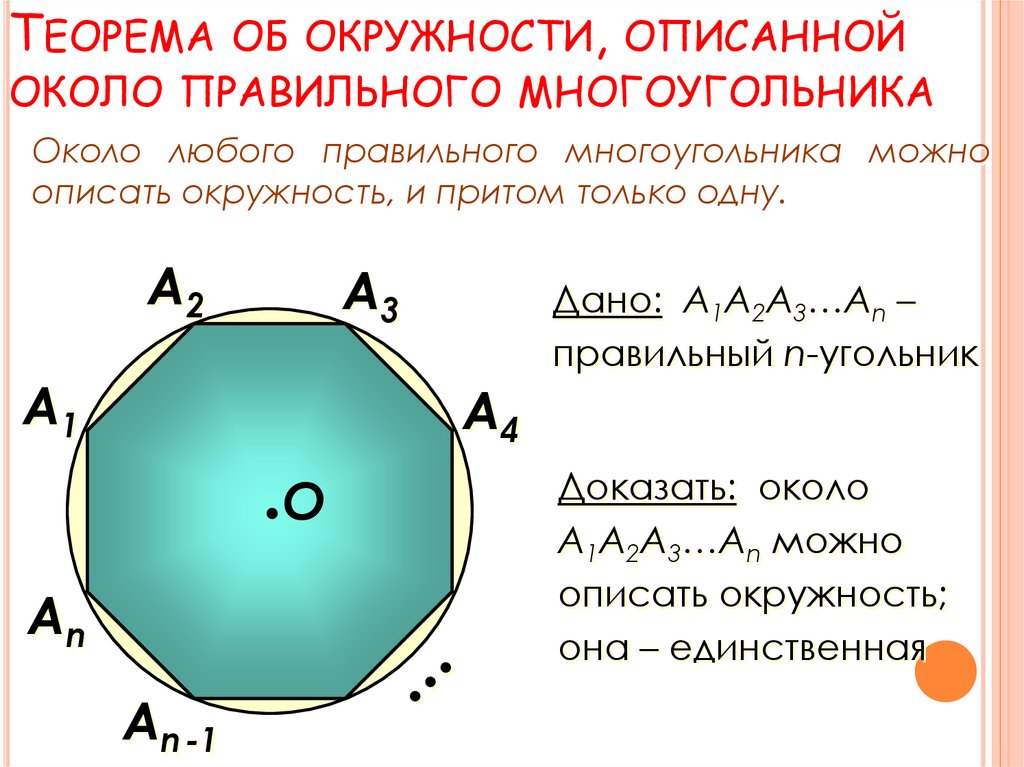
8. Теорема об окружности, описанной около правильного многоугольника
ТЕОРЕМА ОБ ОКРУЖНОСТИ, ОПИСАННОЙОКОЛО ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА
Около любого правильного многоугольника можно
описать окружность, и притом только одну.
А2
А3
А1
Дано: А1А2А3…Аn –
правильный n-угольник
А4
О
Аn
Аn -1
Доказать: около
А1А2А3…Аn можно
описать окружность;
она – единственная
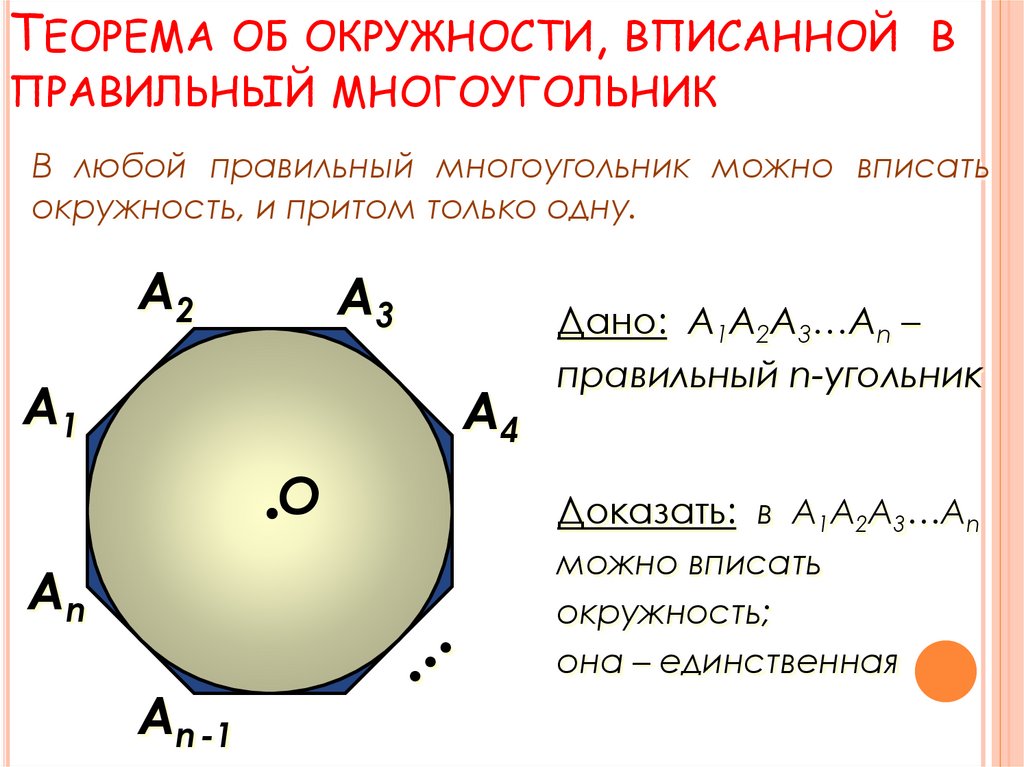
9. Теорема об окружности, вписанной в правильный многоугольник
ТЕОРЕМА ОБ ОКРУЖНОСТИ, ВПИСАННОЙ ВПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК
В любой правильный многоугольник можно вписать
окружность, и притом только одну.
А2
А3
А1
А4
О
Дано: А1А2А3…Аn –
правильный n-угольник
Доказать: в А1А2А3…Аn
можно вписать
окружность;
она – единственная
Аn
Аn -1
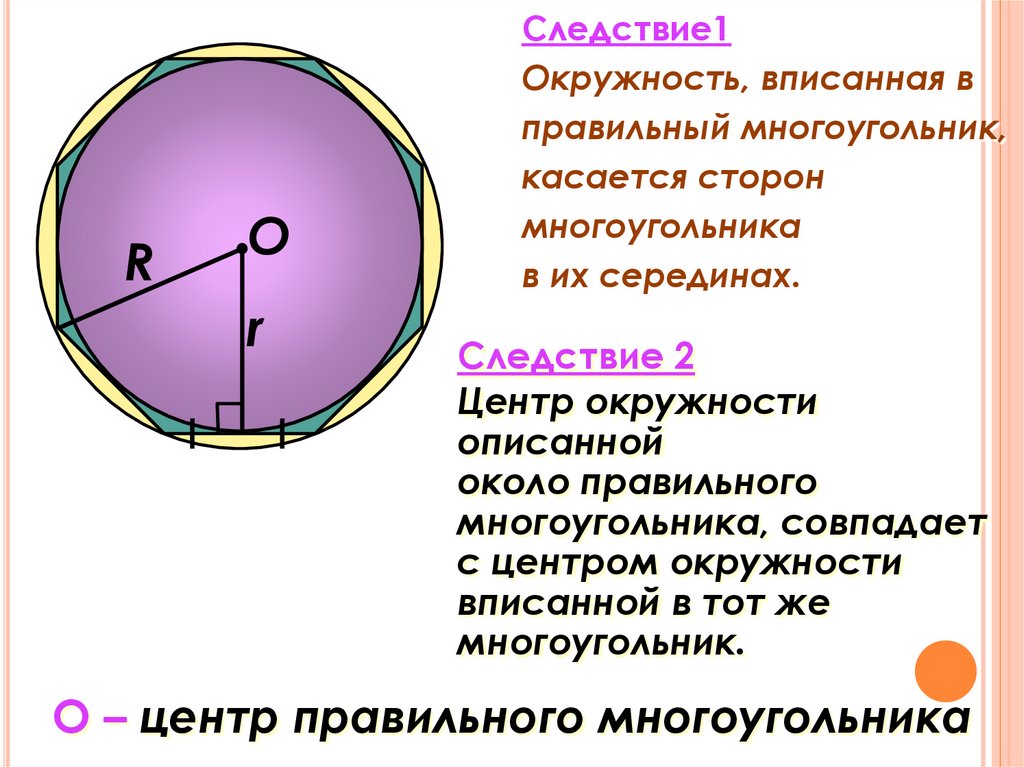
10.
RО
r
Следствие1
Окружность, вписанная в
правильный многоугольник,
касается сторон
многоугольника
в их серединах.
Следствие 2
Центр окружности
описанной
около правильного
многоугольника, совпадает
с центром окружности
вписанной в тот же
многоугольник.
О – центр правильного многоугольника
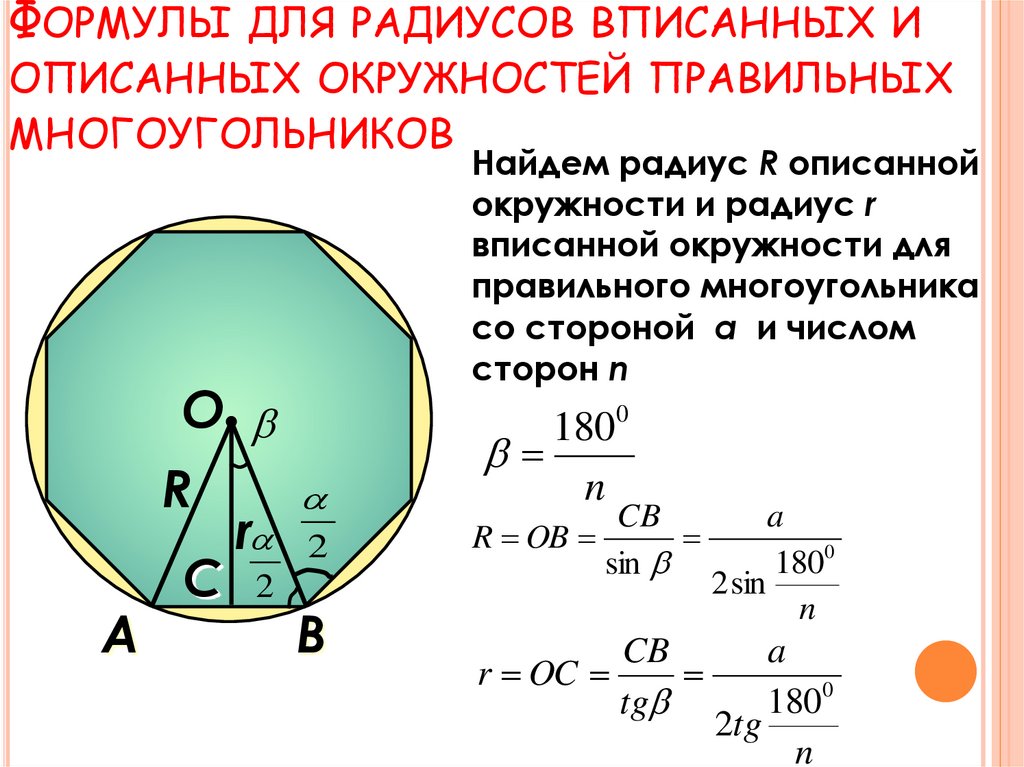
11. Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
ФОРМУЛЫ ДЛЯ РАДИУСОВ ВПИСАННЫХ ИОПИСАННЫХ ОКРУЖНОСТЕЙ ПРАВИЛЬНЫХ
МНОГОУГОЛЬНИКОВ
А
О
R
r
С 2
Найдем радиус R описанной
окружности и радиус r
вписанной окружности для
правильного многоугольника
со стороной a и числом
сторон n
2
В
1800
n
CB
R OB
sin
a
1800
2 sin
n
CB
r OC
tg
a
1800
2tg
n

 Математика
Математика








