Похожие презентации:
Многогранники. Призма
1. 11 класс
Урок-обзор по теме«Многогранники. Призма»
Гржибовская Е.З.,
учитель математики МАОУ «Школа №31»
2. Многогранники
Определение:Многогранник – это такое тело,
поверхность которого состоит из
конечного
числа
плоских
многоугольников
3. Многогранники
4. Многогранники
ВыпуклыеМногогранник
называется
выпуклым, если он
лежит
по
одну
сторону от плоскости
любой его грани.
Невыпуклые
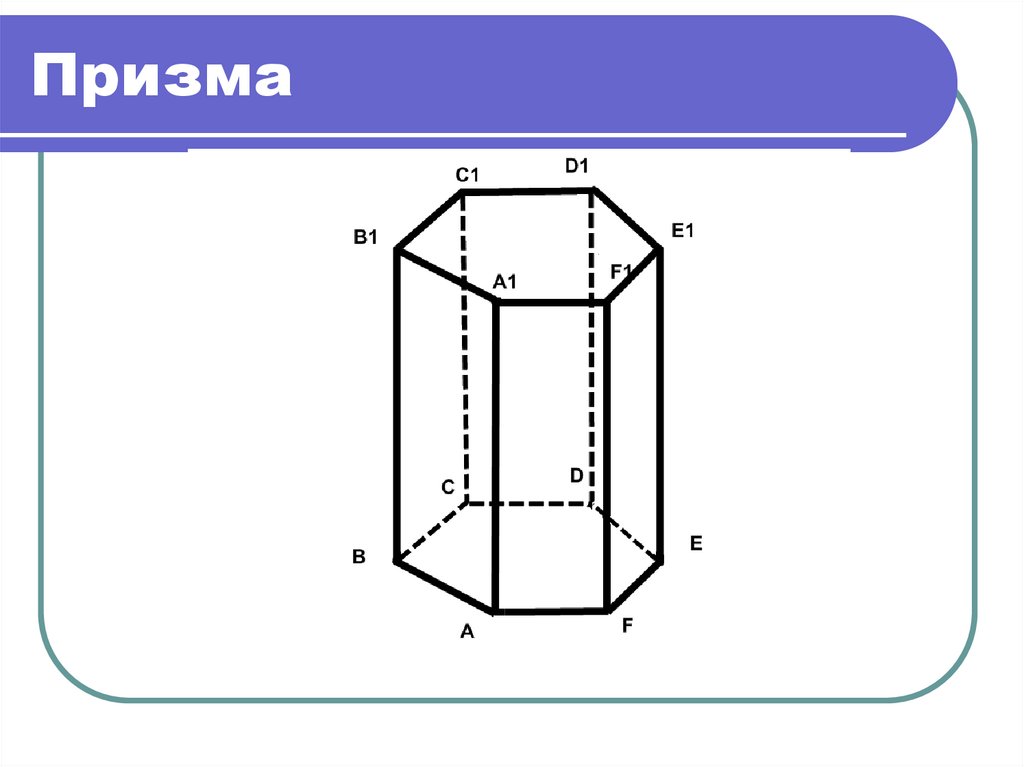
5. Призма
6. ПРИЗМА
Определение:Призма-это
многогранник,
который
состоит
из
двух
плоских
многоугольников, лежащих в разных
плоскостях
и
совмещаемых
параллельным переносом, и всех
отрезков,
соединяющих
соответствующие
точки
этих
многоугольников.
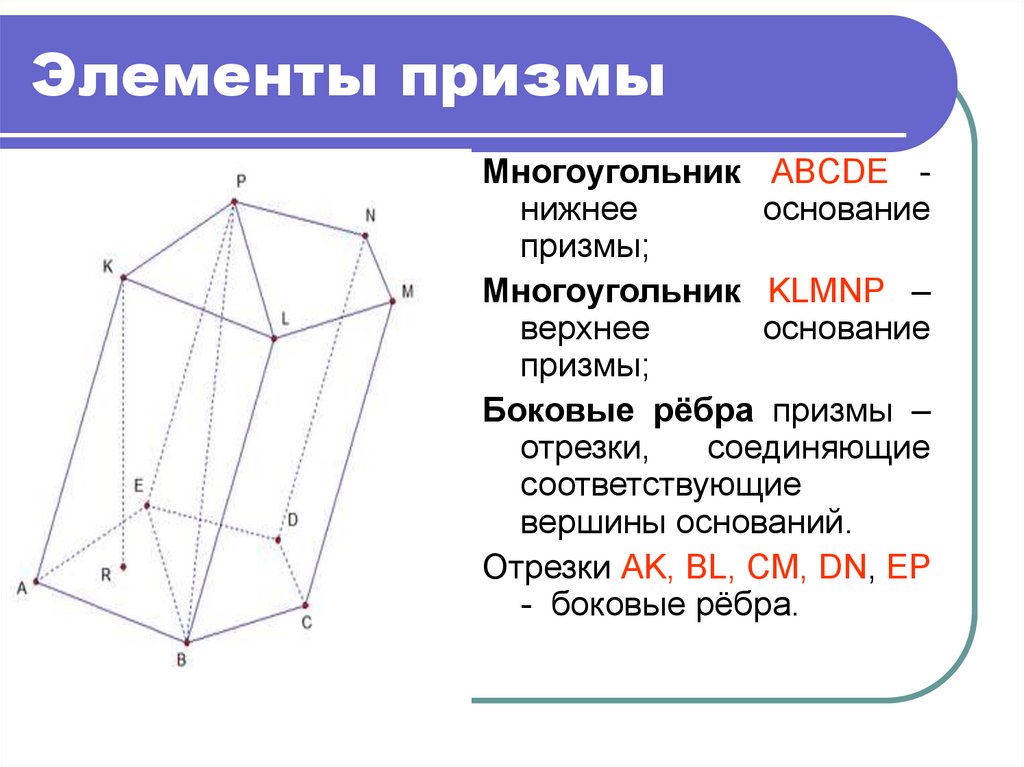
7. Элементы призмы
Многоугольник ABCDE нижнееоснование
призмы;
Многоугольник KLMNP –
верхнее
основание
призмы;
Боковые рёбра призмы –
отрезки,
соединяющие
соответствующие
вершины оснований.
Отрезки AK, BL, CM, DN, EP
- боковые рёбра.
8. Элементы призмы
Высотапризмы
–
это
перпендикуляр, проведённый из
какой-либо
точки
одного
основания призмы к плоскости
другого основния.
Отрезок KR – высота призмы
Диагональ призмы – отрезок,
соединяющий
две
вершины
призмы, не принадлежащие
одной грани.
Отрезок BP – одна из диагоналей
призмы.
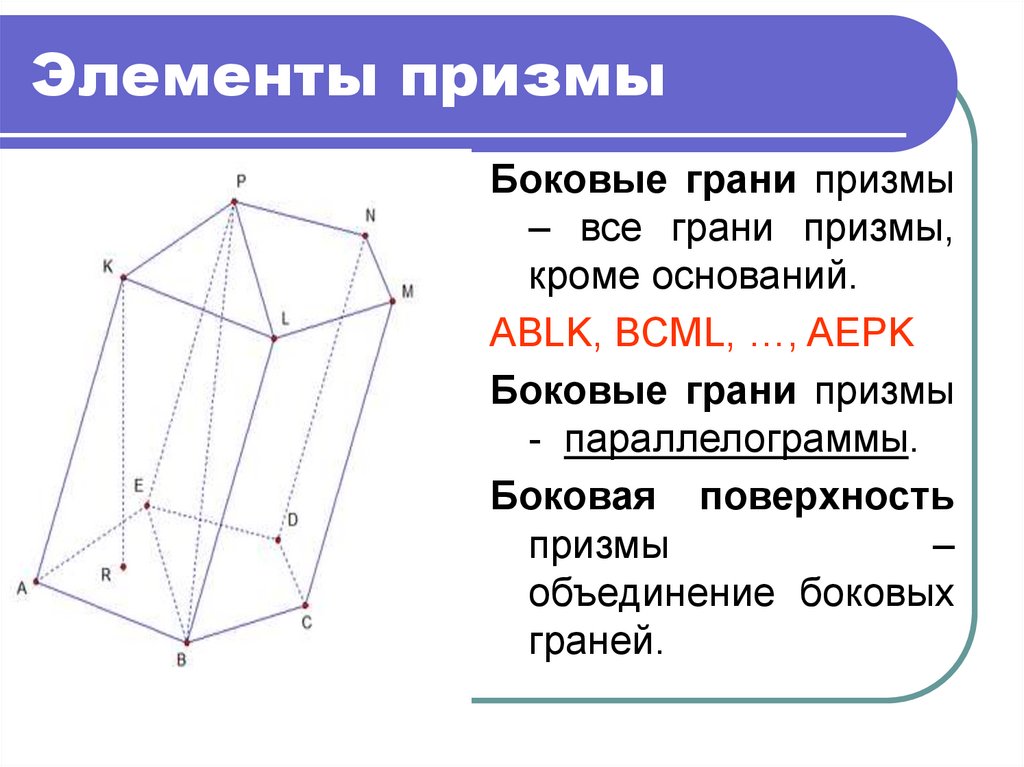
9. Элементы призмы
Боковые грани призмы– все грани призмы,
кроме оснований.
ABLK, BCML, …, AEPK
Боковые грани призмы
- параллелограммы.
Боковая поверхность
призмы
–
объединение боковых
граней.
10. Элементы призмы
Полнаяповерхность
призмы - объединение
оснований и боковой
поверхности.
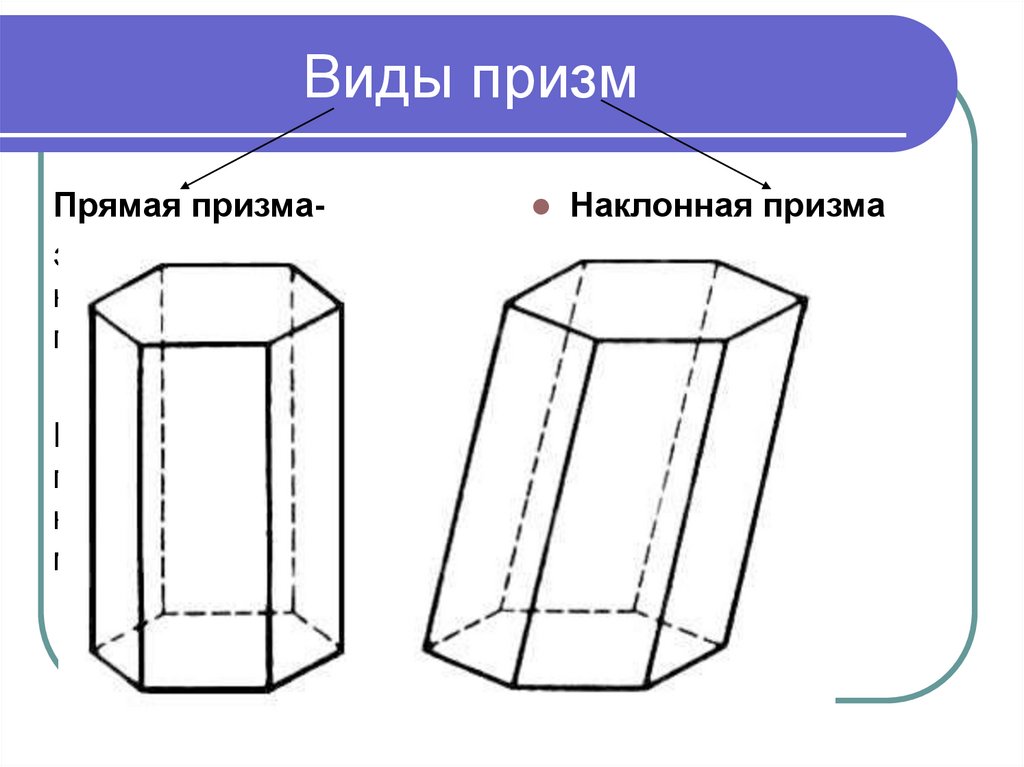
11. Виды призм
Прямая призмаэто призма, боковые рёбракоторой перпендикулярны
плоскостям оснований.
Правильная призма –
прямая призма, основания
которой
правильные
многоугольники.
Наклонная призма
12. Свойства призмы
Основания призмы равныОсновная призмы лежат в
параллельных плоскостях
Боковые грани призмы являются
параллелограммами
Боковые
ребра призмы
параллельны и равны.
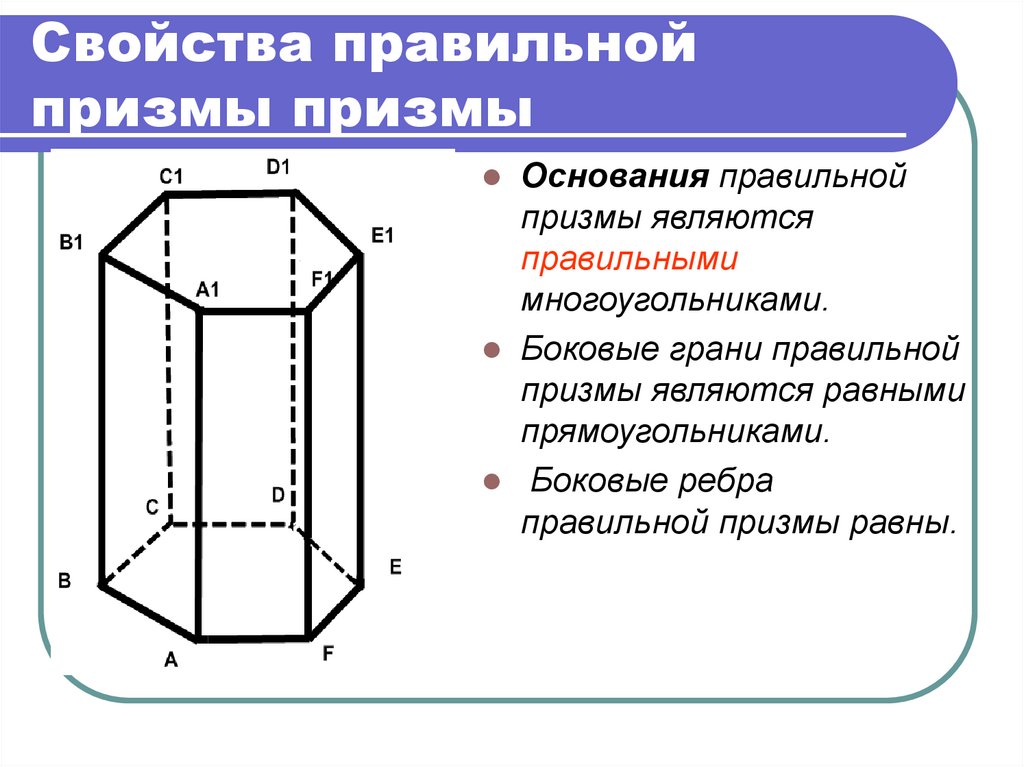
13. Свойства правильной призмы призмы
Основания правильнойпризмы являются
правильными
многоугольниками.
Боковые грани правильной
призмы являются равными
прямоугольниками.
Боковые ребра
правильной призмы равны.
14. Сечения призмы
15. Боковая и полная поверхность призмы
полнойПлощадью
боковой Площадью
поверхности призмы поверхности
сумму
называют
сумму называют
площадей всех её площадей всех её
граней.
боковых граней
Sполн = Sбок + 2Sосн
16. Изобразите таблицу
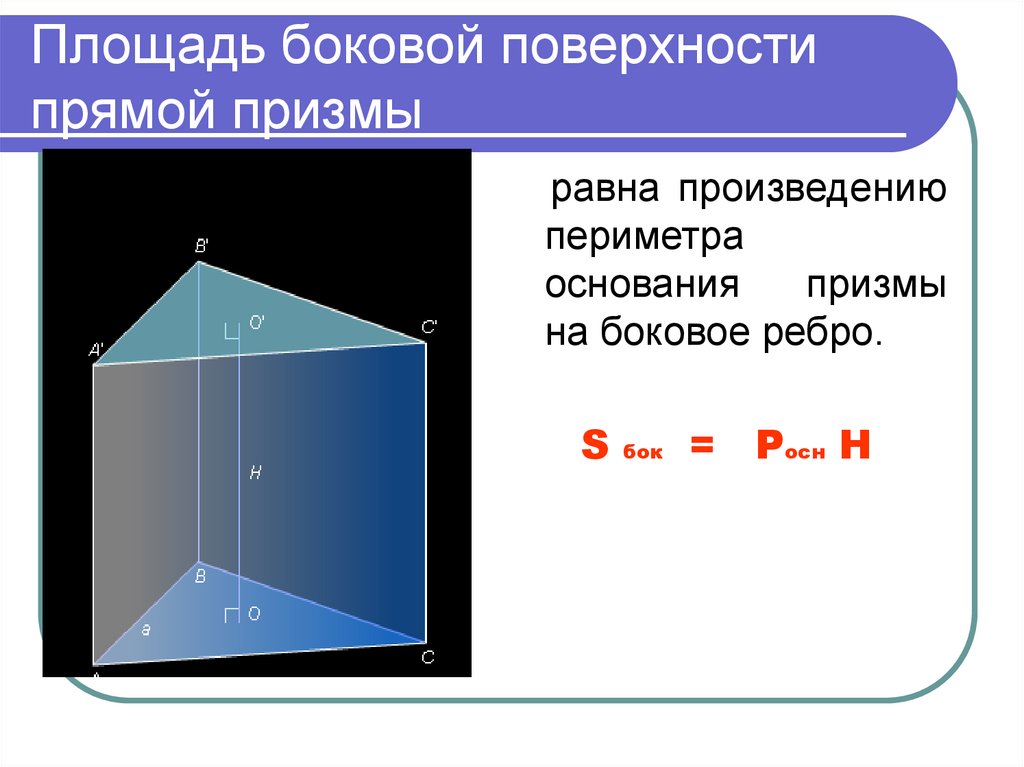
17. Площадь боковой поверхности прямой призмы
равна произведениюпериметра
основания
призмы
на боковое ребро.
S
бок
=
Росн Н
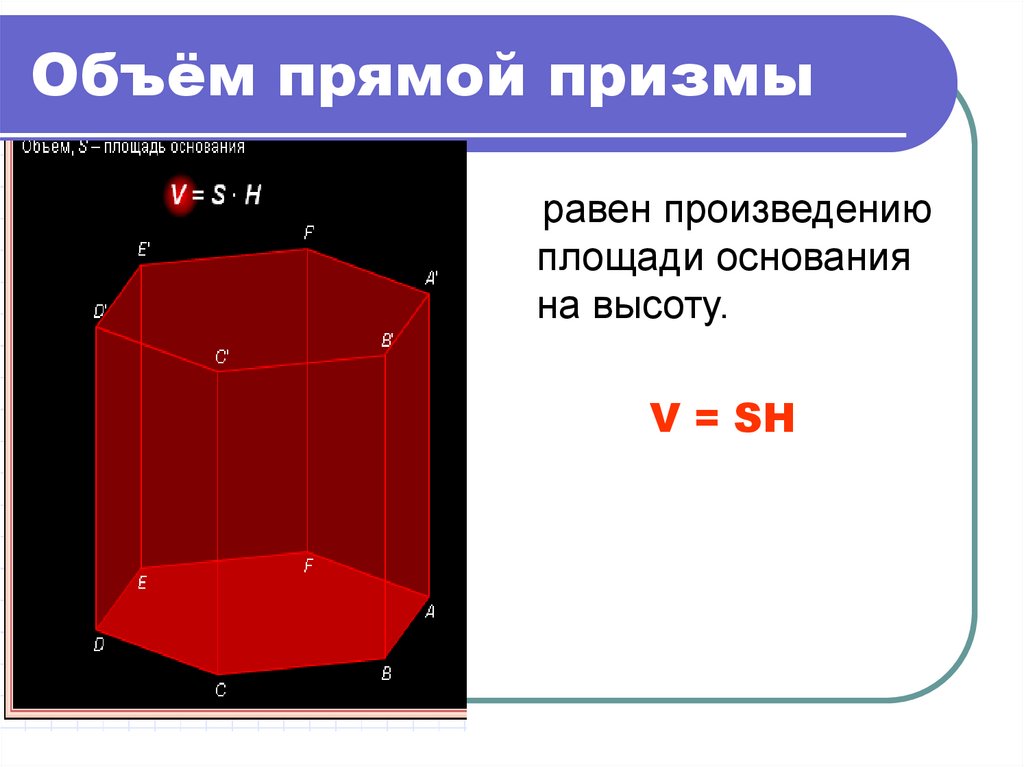
18. Объём прямой призмы
равен произведениюплощади основания
на высоту.
V = SH
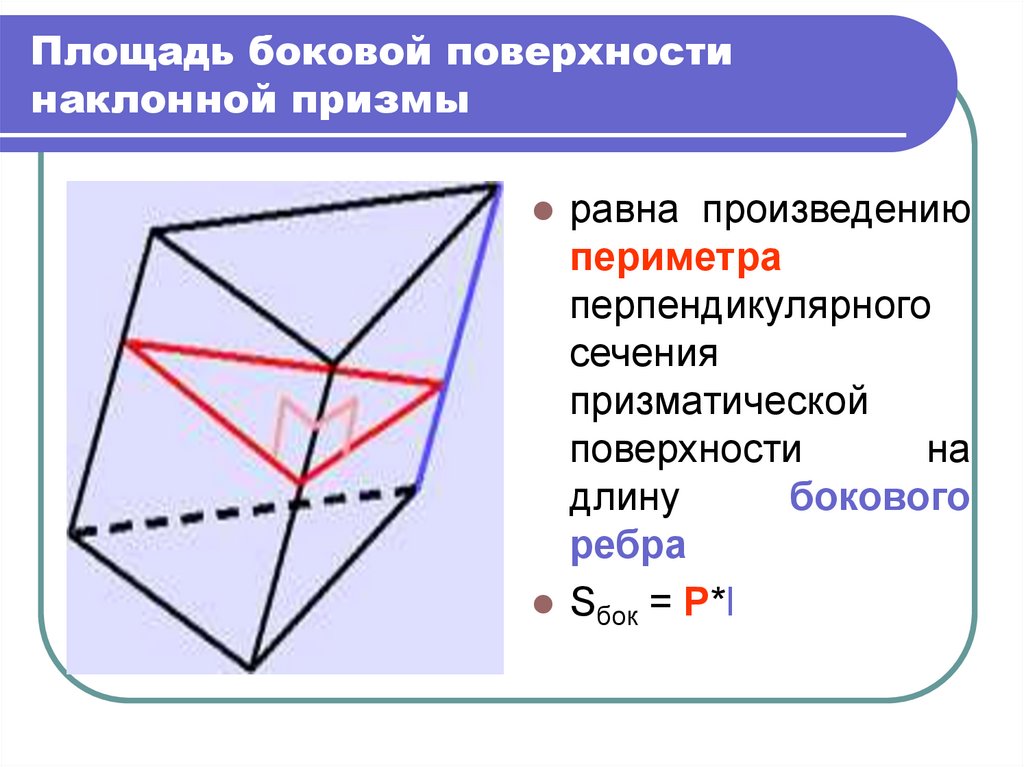
19. Площадь боковой поверхности наклонной призмы
равна произведениюпериметра
перпендикулярного
сечения
призматической
поверхности
на
длину
бокового
ребра
Sбок = P*l
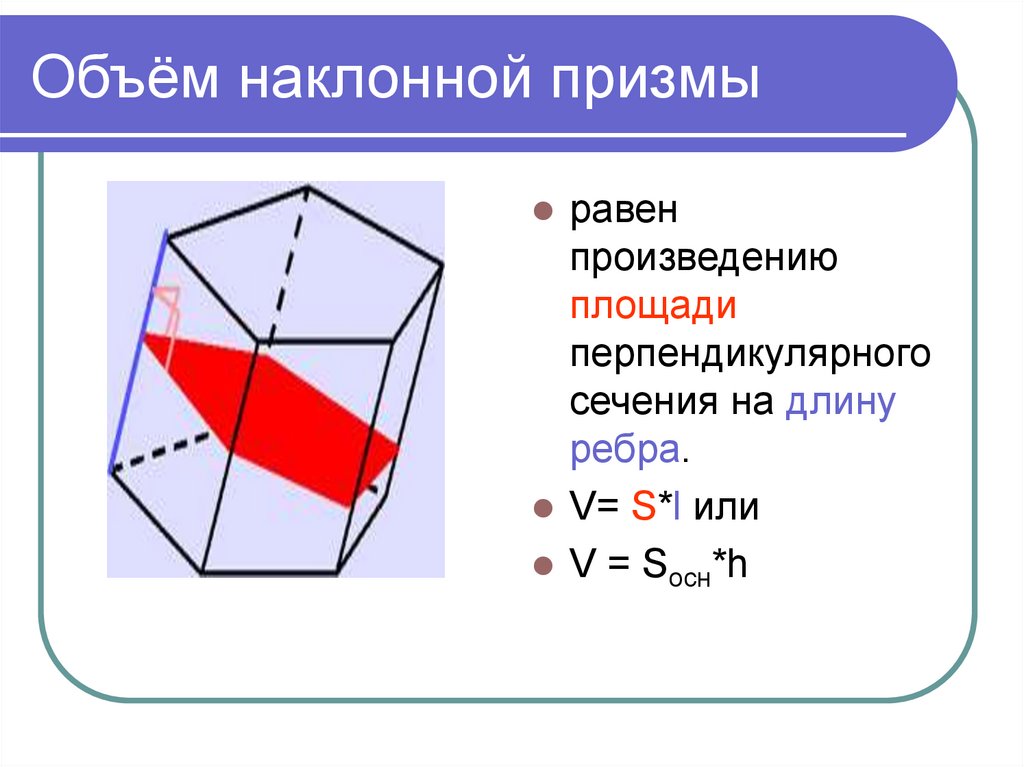
20. Объём наклонной призмы
равенпроизведению
площади
перпендикулярного
сечения на длину
ребра.
V= S*l или
V = Sосн*h











 Математика
Математика








