Похожие презентации:
Многогранники. Призма
1. Теоретическая разминка
1. Чему равна сумма углов в треугольнике?2. Сформулируйте свойство углов при основании
равнобедренного треугольника.
3. Чему равны острые углы равнобедренного
прямоугольного треугольника?
4. Сформулируйте свойство катета, лежащего против
угла в 300.
5. Что называется углом между прямой и плоскостью?
6. Сформулируйте определение прямой
перпендикулярной плоскости.
2. Многогранники
Понятиемногогранника.
Призма.
3.
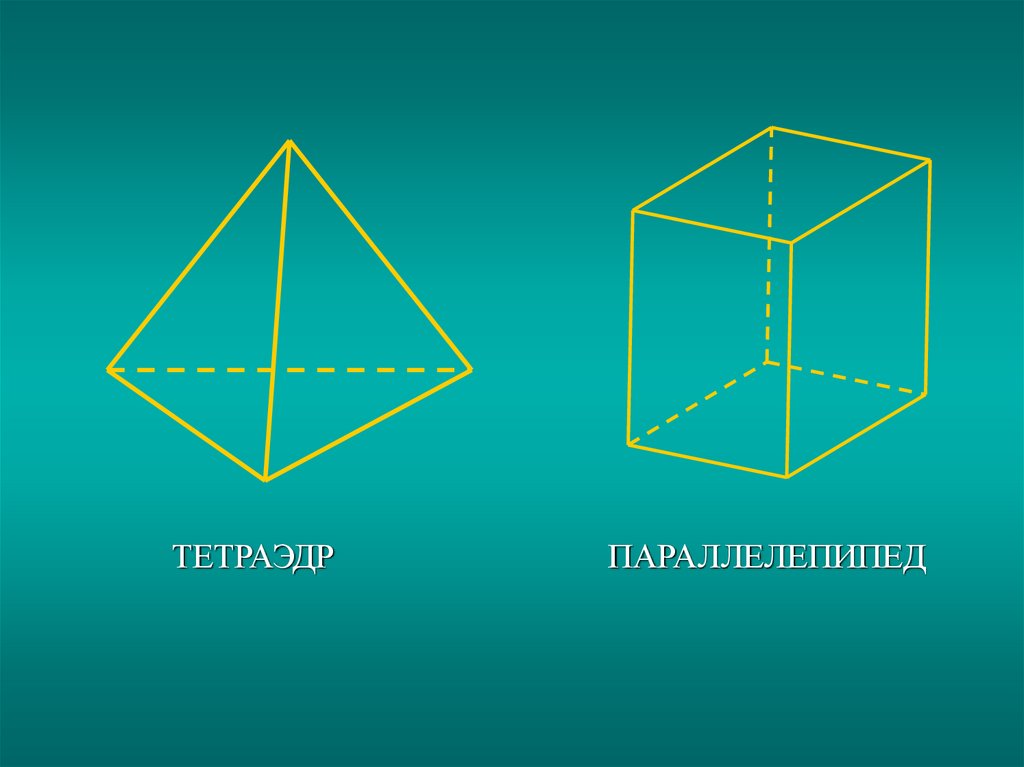
ТЕТРАЭДРПАРАЛЛЕЛЕПИПЕД
4.
Поверхность, составленную измногоугольников и
ограничивающую некоторое
геометрическое тело, будем
называть многогранной
поверхностью или
многогранником
5.
Примеры многогранниковТЕТРАЭДР
РОМБОУСЕЧЁННЫЙ
ИКОСОДОДЕКАЭДР
ПАРАЛЛЕЛЕПИПЕД
КУРНОСЫЙ КУБ
ОКТАЭДР
ЗВЁЗДЧАТЫЙ
ОКТАЭДР
6.
Грани многогранника – многоугольники,из которых составлен многогранник.
Ребра многогранника – стороны граней.
Вершины многогранника – концы рёбер.
Диагональ многогранника – отрезок,
соединяющий две вершины, не
принадлежащие одной грани.
Секущая плоскость – плоскость, по обе
стороны от которой имеются точки
многогранника.
Сечение многогранника – общая часть
многогранника и секущей плоскости.
7. Выпуклые и невыпуклые многогранники
Выпуклыймногогранник
Невыпуклый
многогранник
Многогранник называется выпуклым,
если он расположен по одну сторону от
плоскости каждой его грани.
8.
АBnn
BА11
А2
B
9.
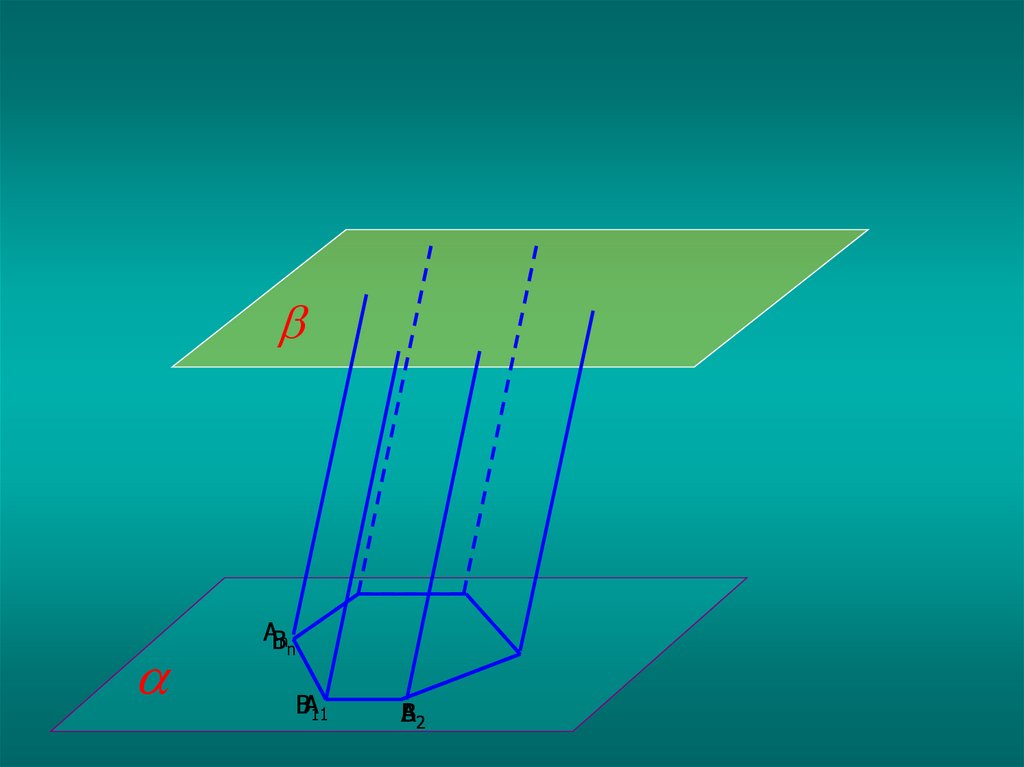
Призма – это многогранник, составленныйиз двух равных многоугольников А1А2…Аn и
В1В2…Вn , расположенных в параллельных
плоскостях, и n параллелограммов.
Многоугольники А1А2…Аn и В1В2…Вn
называются основаниями, а
параллелограммы – боковыми гранями
призмы. Отрезки А1В1, А2В2, …, АnВn
называются боковыми ребрами призмы.
Призму с основаниями А1А2…Аn и В1В2…Вn
обозначают А1А2…АnВ1В2…Вn и называют nугольной призмой.
10.
Граней - 8Рёбер -
18
Вершин - 12
Шестиугольная призма
11.
Перпендикуляр, проведённый из какойнибудь точки одного основания кплоскости другого основания,
называется высотой призмы.
С
А
АВ - высота
СН - высота
В
Н
12.
Еслибоковые
рёбра
призмы
перпендикулярны к основаниям, то
призма
называется
прямой,
в
противном случае наклонной.
Высота прямой призмы равна её
боковому ребру.
Прямая
призма
называется
правильной, если её основания –
правильные многоугольники. У такой
призмы все боковые грани –
равные прямоугольники.
13.
Призмыпрямые
правильные
наклонные
14. Прямые призмы
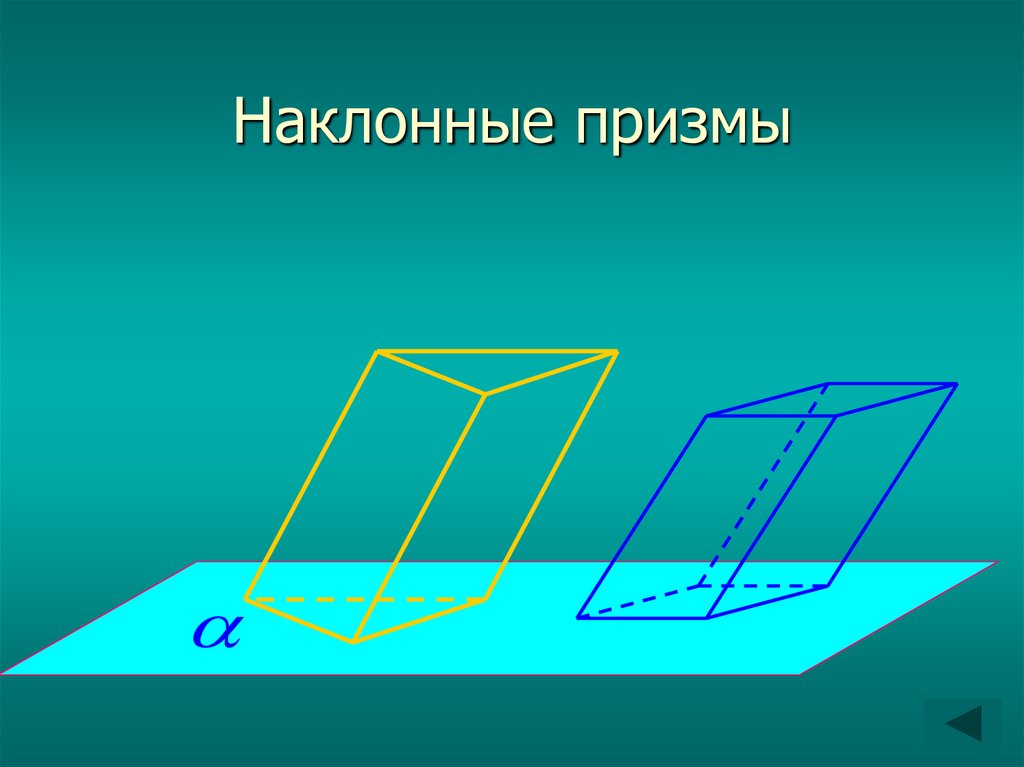
15. Наклонные призмы
16.
Площадь полной поверхности призмы– сумма площадей всех её граней.
Площадь
боковой
поверхности
призмы – сумма площадей её боковых
граней.
Sполн.=Sбок.+2Sосн.
Площадь
боковой
поверхности
прямой призмы равна произведению
периметра основания на высоту призмы.
Sбок.=Ph













 Математика
Математика








